Perbandingan Metode Moving Average dan Single Exponential Smoothing Pada Peramalan Inflasi Kota Purwokerto
on
Jurnal Matematika Vol. 12, No.1, Desember 2022, pp. 49-55
Article DOI: 10.24843/JMAT.2022.v12.i01.p148
ISSN: 1693-1394
Perbandingan Metode Moving Average dan Single Exponential Smoothing pada Peramalan Inflasi Kota Purwokerto
Novita Eka Chandra
Universitas Islam Darul Ulum Lamongan e-mail: novitaeka@unisda.ac.id
Siti Alfiatur Rohmaniah
Universitas Islam Darul Ulum Lamongan e-mail: nia0304@gmail.com
Abstract: Fluctuating inflation rates can lead to economic instability. To overcome this, it is necessary to forecast the value of inflation in the coming year, so that the government can make decisions in regulating economic policy. The data used in this research is inflation data for the city of Purwokerto for 6 years. Based on the results of the data plot, it can be seen that there are no trend and seasonality, so the data can be predicted using the moving average and single exponential smoothing methods. The purpose of this study is to compare the two forecasting methods and determine the best method based on the mean square deviation (MSD) and mean absolute deviation (MAD) values. From the analysis, it is found that the single exponential smoothing method is better used in forecasting inflation data than the moving average method, based on the smallest MSD and MAD values. The results of forecasting the total inflation value of the city of Purwokerto in 2018 were 4,34 percent and were constant.
Keywords : inflation, forecasting, moving average, single exponential smoothing
Abstrak: Laju inflasi yang berfluktuasi dapat menyebabkan ketidakstabilan perekonomian. Untuk mengatasi hal tersebut diperlukan adanya peramalan nilai inflasi pada tahun yang mendatang, supaya pemerintah dapat mengambil keputusan dalam mengatur kebijakan perekonomian. Data yang digunakan pada penelitian ini adalah data inflasi kota Purwokerto selama 6 tahun. Berdasarkan hasil plot data terlihat tidak ada trend dan ada musiman, maka data dapat diramalkan menggunakan metode moving average dan single exponential smoothing. Tujuan penelitian ini untuk membandingkan kedua metode peramalan dan menentukan metode yang terbaik berdasarkan nilai mean square deviation (MSD) dan mean absolute deviation (MAD). Dari analisis yang dilakukan diperoleh bahwa metode single exponential smoothing lebih baik digunakan dalam peramalan data inflasi dibandingkan metode moving average, berdasarkan nilai MSD dan MAD terkecil. Hasil peramalan total nilai inflasi kota Purwokerto pada tahun 2018 sebesar 4,34 persen dan konstan.
Kata Kunci: inflasi, peramalan, moving average, single exponential smoothing
Inflasi merupakan salah satu dasar guna menentukan kebijakan pemerintah. Selain itu, inflasi juga sebagai tolok ukur perekonomian. Naik turunnya inflasi yang dikenal dengan laju inflasi sebagai indikator ketidakstabilan keadaan perekonomian. Inflasi yang tinggi menyebabkan pendapatan menurun, sehingga masyarakat menjadi miskin. Sebaliknya, inflasi ringan dapat membantu pertumbuhan ekonomi. Apabila perekonomian stabil, maka kesejahteraan masyarakat pun tercapai. Berdasarkan data Badan Pusat Statistik (BPS) Kabupaten Banyumas tahun 2012, dari tahun ke tahun data inflasi kota Purwokerto mengalami fluktuatif. Terlihat dari tahun 2012 sampai 2017, laju inflasi kota Purwokerto mengalami fluktuatif. Untuk mengantisipasi kestabilan nilai inflasi diperlukan adanya penaksiran nilai inflasi tahun yang akan datang. Peramalan nilai inflasi ini menggunakan beberapa metode peramalan. Peramalan bertujuan untuk meramalkan kondisi yang akan datang dengan menggunakan data historis dan mengekstrapolasikan pola tersebut ke masa depan. Metode yang dapat digunakan untuk peramalan yaitu moving average dan single exponential smoothing. Tujuan dari penelitian ini untuk meramalkan inflasi kota Purwokerto menggunakan metode moving average dan single exponential smoothing. Selanjutnya, dilakukan perbandingan kedua metode untuk diperoleh metode peramalan yang paling baik. Metode peramalan terbaik dipilih berdasarkan nilai ukuran kesalahan yaitu MSD dan MAD yang terkecil.
Peramalan merupakan suatu teknik memperkirakan suatu nilai pada masa yang akan datang dengan menggunakan data masa lalu maupun data masa saat ini Aswi dan Sukarna (2006) dan Chandra dan Sarinem (2016). Peramalan dibedakan menjadi dua yaitu peramalan kualitatif dan peramalan kuantitatif. Peramalan kuantitatif membutuhkan informasi masa lalu yang berupa data numerik. Salah satu model peramalan kuantitatif yaitu model deret waktu. Model deret waktu (time series) digunakan untuk meramalkan kondisi yang akan datang berdasarkan kondisi masa lalu. Metode peramalan yang digunakan yaitu metode moving average dan single exponential smoothing. Kedua metode peramalan cocok digunakan untuk data yang stasioner. Data stasioner merupakan data yang tidak berubah dengan pergeseran waktu. Artinya data tidak berfluktuasi naik maupun turun Rosadi (2016), dan Khamaludin, Agustianna, Darmawan, dan Dermawan (2019).
Data yang digunakan dalam peramalan sekunder yang diambil dari BPS Kabupaten Banyumas yaitu data inflasi Kota Purwokerto tiap bulan selama enam tahun terakhir. Jumlah data pengamatan sebanyak 60 bulan sebagai in-sample dan 12 bulan sebagai out-
sample. Peramalan menggunakan bantuan software MINITAB. Berikut langkah-langkah dalam melakukan peramalan :
-
1. Memeriksa kestasioneran data dengan melihat plot time series data.
-
2. Melakukan peramalan dengan moving average.
Metode moving average (MA) adalah metode yang menggunakan rata-rata dari data periode sebelumnya (i = 1,2,...,t)untuk meramalkan periode berikutnya (t +1). Secara aljabar, MA dapat dituliskan sebagai berikut (Makridakis, Wheelwright, McGee, Andriyanto, dan Basith, 1999) :
Ft+1 = X1 + X2 +... + Xt =1 ∑ X, i = 1,2,..., t t t~
dengan Ft+1 menyatakan nilai ramalan periode ke t +1, Xi- adalah nilai data aktual periode ke i, dan t menyatakan banyaknya periode dalam MA.
-
3. Melakukan peramalan dengan single exponential smoothing.
Metode single exponential smoothing (SES) merupakan pengembangan dari metode MA. Pada metode ini diberikan nilai pembobotan di setiap nilai data pengamatan periode masa lalu. Ramalan F didasarkan atas pembobotan observasi yang terakhir Xt dengan suatu nilai bobot α dan pembobotan ramalan yang terakhir sebelumnya Ft dengan suatu bobot 1 - α. Dengan demikian, bentuk umum yang digunakan dalam menghitung ramalan dengan metode SES yaitu
Ft+1 = αXt + (1 - α)Ft.
Metode ini mengurangi masalah penyimpangan data karena tidak perlu lagi menyimpan semua atau sebagian data historis (Makridakis et al., 1999).
-
4. Melakukan perbandingan metode peramalan berdasarkan nilai ukuran kesalahan. Untuk membandingkan beberapa metode dapat dilihat dari nilai pengukuran kesalahan. Nilai pengukuran kesalahan ini merupakan nilai selisih dari nilai ramalan dengan nilai aktualnya. Ada beberapa pengukuran kesalahan menurut (Makridakis et al., 1999), yaitu :
-
a. Mean absolute deviation (MAD)
n
MAD = - ∑ X, — F
n t=1
-
b. Mean square deviation (MSD)
n
MSD = - ∑(Xt - Ft )
n t=1
dengan X adalah data aktual periode ke t dan F adalah nilai ramalan periode ke t, serta n adalah banyaknya periode ramalan yang dilakukan
Data yang digunakan dalam penelitian ini adalah data inflasi Kota Purwokerto selama 6 tahun terakhir (Tabel 1). Jumlah semua data ada 72 bulan. Data kemudian dibagi menjadi dua, yaitu 60 bulan (5 tahun terakhir) sebagai in-sample (initialization) dan 12 bulan (satu tahu terakhir) sebagai out-sampel (test set). Data inflasi Kota Purwokerto digunakan untuk meramalkan 12 bulan ke depan.
Tabel 1. Data Inflasi Kota Purwokerto
|
Bulan |
Inflasi (persen) Tahun Ke- | |||||
|
2012 |
2013 |
2014 |
2015 |
2016 |
2017 | |
|
Januari |
0,68 |
1,63 |
0,82 |
-0,13 |
0,57 |
1,05 |
|
Februari |
0,56 |
0,4 |
0,51 |
-0,67 |
-0,29 |
0,56 |
|
Maret |
-0,21 |
0,44 |
0,08 |
0,05 |
0,55 |
-0,01 |
|
April |
0,09 |
-0,17 |
-0,08 |
0,15 |
-0,45 |
-0,04 |
|
Mei |
0,43 |
0,06 |
0,08 |
0,47 |
0,12 |
0,66 |
|
Juni |
0,33 |
1,48 |
0,48 |
0,57 |
0,38 |
0,98 |
|
Juli |
0,84 |
2,84 |
0,82 |
0,84 |
0,87 |
0,19 |
|
Agustus |
0,85 |
1,08 |
0,43 |
0,13 |
-0,51 |
0,54 |
|
September |
0,17 |
-0,71 |
-0,24 |
-0,02 |
0,02 |
-0,06 |
|
Oktober |
0,29 |
0,88 |
0,41 |
0,02 |
0,02 |
0,09 |
|
November |
0,08 |
0,04 |
1,38 |
0,16 |
0,77 |
0,39 |
|
Desember |
0,53 |
0,29 |
2 |
0,93 |
0,37 |
0,57 |
Sumber: BPS Kabupaten Banyumas
Selanjutnya, memeriksa kestasioneran dari plot time series data in sample.
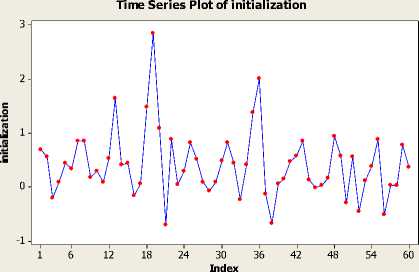
Gambar 1. Plot Time Series Data In Sample
Dari gambar plot time series pada Gambar 1 , dapat dilihat bahwa pada data inflasi tidak terdapat efek trend dan fluktuasi data yang cenderung stasioner dari waktu ke waktu. Selain itu, terdapat juga indikasi pola musiman. Karena tidak ada efek trend dan terdapat musiman, maka metode peramalan yang mungkin diterapkan adalah moving average, dan single exponential smoothing. Untuk metode single exponential smoothing pada penelitian ini menggunakan bobot (α) yang optimal berdasarkan hasil perhitungan
MINITAB sebesar 0,0308303. Berikut ini perbandingan data aktual out-sample dengan hasil peramalan menggunakan metode moving average dan single exponential smoothing.
Tabel 2. Perbandingan Data Out-Sample dengan Hasil Peramalan
|
Periode |
Out Sample |
MA |
SES |
|
61 |
1,05 |
0,201667 |
0,373763 |
|
62 |
0,56 |
0,201667 |
0,373763 |
|
63 |
-0,01 |
0,201667 |
0,373763 |
|
64 |
-0,04 |
0,201667 |
0,373763 |
|
65 |
0,66 |
0,201667 |
0,373763 |
|
66 |
0,98 |
0,201667 |
0,373763 |
|
67 |
0,19 |
0,201667 |
0,373763 |
|
68 |
0,54 |
0,201667 |
0,373763 |
|
69 |
-0,06 |
0,201667 |
0,373763 |
|
70 |
0,09 |
0,201667 |
0,373763 |
|
71 |
0,39 |
0,201667 |
0,373763 |
|
72 |
0,57 |
0,201667 |
0,373763 |
Selanjutnya, dilakukan perbandingan nilai pengukuran kesalahan dari kedua metode baik secara in-sample maupun out-sample. Berikut hasil perbandingan nilai pengukuran kesalahannya.
Tabel 3. Perbandingan Nilai Pengukuran Kesalahan
|
Data |
MA |
SES | ||
|
MAD |
MSD |
MAD |
MSD | |
|
In-sample |
0,507 |
0,461 |
0,454 |
0,382 |
|
Out-sample |
0,348056 |
0,177819 |
0,319373 |
0,13573 |
Berdasarkan Tabel 3, terlihat bahwa untuk data in-sample dan out-sample nilai MAD dan MSD metode single exponential smoothing lebih kecil, dibandingkan metode moving average. Oleh karena itu, metode single exponential smoothing yang digunakan dalam melakukan peramalan data inflasi 12 bulan ke depan. Berikut hasil peramalan dari data inflasi kota Purwokerto pada bulan ke 74 sampai 85 (satu tahun ke depan).
Tabel 4. Hasil Peramalan
|
Periode |
Bulan Tahun Ke-8 |
Ramalan |
|
74 |
Januari |
0,362379 |
|
75 |
Februari |
0,362379 |
|
76 |
Maret |
0,362379 |
|
77 |
April |
0,362379 |
|
78 |
Mei |
0,362379 |
|
79 |
Juni |
0,362379 |
|
80 |
Juli |
0,362379 |
|
81 |
Agustus |
0,362379 |
|
82 |
September |
0,362379 |
|
83 |
Oktober |
0,362379 |
|
84 |
November |
0,362379 |
|
85 |
Desember |
0,362379 |
Apabila data ramalan digabungkan dengan data asli, maka plot time series yang diperoleh sebagai berikut :
Time Series Plot of data aktual dan ramalan

-1 —I-------------1---------------1---------------1---------------1---------------1---------------1--------------1---------------1---------------1---------------Γ^
1 8 16 24 32 40 48 56 64 72 80
Index
Gambar 2. Plot Time Series Gabungan Data Aktual dan Ramalan
Dari Tabel 4 terlihat hasil peramalan inflasi kota Purwokerto pada awal tahun 2018 sebesar 0,362379 persen, selanjutnya inflasi bernilai stabil . Dengan total inflasinya pada satu tahun ke depan sebesar 4,348548 persen. Oleh karena itu, pemerintah kota Purwokerto harus membuat keputusan kebijakan perekonomiannya dengan tepat supaya inflasi tahun berikutnya tidak mengalami kenaikan yang tinggi.
Berdasarkan hasil dan pembahasan yang dilakukan, diperoleh bahwa untuk meramalkan data inflasi kota Purwokerto metode single exponential smoothing memberikan hasil
yang lebih baik dibandingkan metode moving average. Hal ini terlihat dari nilai MAD dan MSD yang diberikan oleh metode single exponential smoothing lebih kecil dibandingkan metode moving average. Berdasarkan hasil peramalan dengan metode single exponential smoothing diperoleh bahwa nilai total inflasi kota Purwokerto sebesar 4,34 persen. Saran untuk penelitian selanjutnya, sebaiknya menggunakan metode triple exponential smoothing yang mengakomodasi musiman sehingga peramalan inflasi bulanan tidak konstan.
Daftar Pustaka
Aswi dan Sukarna. (2006). Analisis Deret Waktu : Teori dan Aplikasi. Makasar: Andira Publisher.
Chandra, N. E., & Sarinem, S. (2016). Peramalan Penyebaran Jumlah Kasus Virus Ebola di Guinea dengan Metode ARIMA. Unisda Journal of Mathematics and Computer Science (UJMC), 2(1), 28–35.
Khamaludin, Agustianna, V., Darmawan, A., & Dermawan, M. L. (2019). Peramalan Penjualan Hijab Sxproject Menggunakan Metode Moving Average dan Exponential Smoothing. Jurnal Keilmuan Dan Aplikasi Teknik, 6(2), 13–16.
Makridakis, S., Wheelwright, S. C., McGee, V. E., Andriyanto, U. S., & Basith, A. (1999). Metode dan Aplikasi Peramalan Jilid 1. Jakarta: Erlangga.
Rosadi, D. (2016). Analisis Runtun Waktu dan Aplikasinya dengan R. Yogyakarta: UGM Press.
55
Discussion and feedback