Dimensi Metrik Pada Graf Starbarbell dan Hasil Operasi Edge Corona Pada Graf Cycle dan Graf Path
on
Jurnal Matematika Vol. 10, No.1, Juni 2020, pp. 32-43
Article DOI: 10.24843/JMAT.2020.v10.i01.p121
ISSN: 1693-1394
Dimensi Metrik Pada Graf Starbarbell dan Hasil Operasi Edge Corona Pada Graf Cycle dan Graf Path
Putri Dea Sari
Universitas Sebelas Maret e-mail: pdeasari@gmail.com
Tri Atmojo Kusmayadi
Universitas Sebelas Maret e-mail: tri.atmojo.kusmayadi@staff.uns.ac.id
Abstract: Let G be a connected graph with vertex set V (G) and edge set E(G). Distance between vertex U and V is the shortest path from U to V, denoted by d(u,v). For an ordered set W c V(G),W is resolving set of G if every pair of vertices in G are resolved by some vertex of W. Resolving set with minimum cardinality is called metric basis of G. The number of element from some basis in G is called metric dimension, denoted by dim (G). In this research, we determine the metric dimension of starbarbell graph and edge corona graph Cm 0 Pn . The results show that the metric dimension of starbarbell graph is dim (SSmpmjι ,mn) — ∑jL1G∏f 2) ; dim( Cm o Pn) = 2 for 71 = 1 , 771 = 3 , or 771 even ( 771 > 4 ); dim( Cm o P„) = 3 for 71 = 1 and 771 odd ( 771 > 5 );
dim(Cm o Pn) = 2 |— for 711 > 3 and 71 > 2.
or m = 3 andn ≥ 2; and also dim (Cm o Pn} = m.
Keywords: metric dimension, resolving set, starbarbell graph, Cm 0 Pn graph
Abstrak: Misal G adalah graf terhubung dengan himpunan vertex V(G) dan himpunan edge E(G). Jarak di antara dua vertex u dan V adalah panjang path terpendek dari U ke V, yang dinyatakan dengan d(u,v). Untuk suatu himpunan terurut W c V(G),W adalah himpunan pembeda dari G jika setiap pasang vertex dalam G dibedakan oleh suatu vertex dari W. Himpunan pembeda dengan kardinalitas minimum disebut basis metrik dari G . Banyaknya elemen dari suatu basis dalam G disebut dimensi metrik, dinyatakan dengan dim (G). Dalam penelitian ini ditentukan dimensi metrik dari graf starbarbell dan graf edge corona Cm o Pn . Hasilnya menunjukkan bahwa dimensi metrik dari graf starbarbell adalah dim (SBmpm2_mn) = ∑^,(mi - 2) ; dim(Cm o Pn) = 2 untuk 71 = 1 , 771 = 3 , atau 771 genap (771 > 4); dim( Cm o Pn) = 3 untuk 71 = 1 dan 771 ganjil ( m ≥ 5 );
dim( Cm
opπ)=2 ≥ + untuk m = 3 dan 71 ≥ 2; dan juga dim(Cm o Pn) = m
untuk m > 3 dan 71 > 2 .
Kata kunci: dimensi metrik, himpunan pembeda, graf starbarbell, grafCm° Pn
Tahun 1975, konsep dimensi metrik muncul dari himpunan pembeda yang diperkenalkan oleh Slater [9], yang mendefinisikan himpunan pembeda atau locating set W sebagai himpunan dari vertex-vertex pada suatu graf G sedemikian sehingga untuk setiap vertex di G akan dihasilkan jarak yang berbeda terhadap setiap vertex di W. Dimensi metrik adalah kardinalitas minimum dari himpunan pembeda W. Kemudian Harary dan Melter [6] pada tahun 1976 menyebutkan himpunan pembeda sebagai resolving set. Hasil operasi edge corona dari graf cycle dan graf path dinotasikan dengan Cm ⋄ Pn. Graf ini terbentuk dari salinan graf cycle Cm dan m salinan graf path Pn kemudian menggabungkan dengan dua vertex ujung dari ei ∈ E(Cm) ke setiap vertex vj ∈ V (Pn) pada salinan ke-i dengan i = 1, 2, ..., m1 dan j = 1, 2, ..., n2.
Beberapa peneliti telah menemukan dimensi metrik pada beberapa kelas graf. Tahun 2000, Chartrand et al. [5] meneliti dimensi metrik graf path Pn, graf cycle Cn, dan graf lengkap Kn. Tahun 2005, Caceres et al. [3] meneliti dimensi metrik graf fan. Tahun 2009, Caceres et al. [4] meneliti dimensi metrik pada graf tak hingga. Tahun 2011, Bača et al. [1] meneliti dimensi metrik pada graf bipartit k-reguler. Tahun 2016, Kusmayadi et al. [8] meneliti dimensi metrik pada graf sunflower, graf t-fold wheel, dan graf K1 + (Pn ⊙ Pm). Widodo [10] menentukan dimensi metrik dari helm graph dan double cones graph. Hasil penelitian tersebut membuat penulis tertarik untuk mencari dimensi metrik pada kelas graf lain yang belum pernah ditentukan, yaitu dimensi metrik pada graf starbarbell dan graf Cm ⋄ Pn.
Metode yang digunakan dalam penelitian ini adalah kajian pustaka yaitu dengan mengumpulkan referensi berupa buku-buku, jurnal maupun tulisan-tulisan yang dimuat di situs web. Dari metode ini, dapat ditentukan dimensi metrik pada graf starbarbell dan graf Cm ⋄ Pn.. Langkah-langkah yang dilakukan dalam penelitian ini diuraikan sebagai berikut.
-
1) Menentukan himpunan pembeda W pada graf starbarbell dan graf Cm ⋄ Pn..
-
2) Menghitung jarak setiap vertex dengan W yang telah ditentukan, sedemikian sehingga setiap dua vertex berbeda pada graf starbarbell dan graf Cm ⋄ Pn. mempunyai representasi yang berbeda terhadap W .
-
3) Menentukan dimensi metrik berdasarkan hasil yang diperoleh pada Langkah 2) pada graf starbarbell dan graf Cm ⋄ Pn.
-
4) Membuat pembuktian dengan menyusun lema dan teorema berdasarkan hasil yang diperoleh.
-
5) Membuat kesimpulan
Budianto dan Kusmayadi [2] mendefinisikan graf starbarbell $ B m1,m2,...,mn merupakan graf yang terbentuk dari sebuah graf star ^±ln dan n graf lengkap ^mi kemudian menggabungkan satu vertex dari masing-masing ^ml dengan leaf ke- ' pada
^ljH dengan mi ≥ 3 , 1 ≤ i ≤ n, dann≥ 2.
pada Gambar 1.
Ilustrasi dari graf starbarbell dapat dilihat

Gambar 1. Graf starbarbell ^^Bm^m„ ,∙.vmn
Lemma 3.1. Vertex pusat U tidak termuat dalam basis manapun pada suatu graf starbarbell o d mvm2,,,.,mn' .
BUKTI. Dibuktikan dengan kontradiksi. Andai F adalah basis pada graf starbarbell ^ ^mlfπL2,.,.,mn yang memuat vertex pusat U . Karena p ∖w bukan basis, terdapat vertex v, v EF ^Bm^ m^f t m sedemikian sehingga d(v,x) = d(v,' ,x) untuk setiap X ∈ P∖{u} . Jelas bahwa p = W bukan basis, sehingga P ∖{ul ≠ $ . Jika tidak
berlaku dan maka dan bukan basis pada graf
CE? ∕ __ .
starbarbell . Misal diasumsikan dan tanpa mengurangi
keumuman, adalah vertex . Pada kasus ini, diperoleh untuk
setiap . Artinya bukan basis. Sehingga terbukti bahwa vertex pusat tidak
termuat dalam basis manapun. □
Teorema 3.2. Untuk setiap graf starbarbell dengan untuk setiap
dan berlaku
71
^(SB"^,..,^) = ^(™£ ^ 2)'
BUKTI. Diberikan graf starbarbell dengan untuk setiap
dan
-
i) Akan ditunjukkan bahwa
Dengan Lema 3.1, dipilih himpunan dengan dan
Kardinalitas dari W yaitu Diperoleh representasi
dari setiap vertex pada terhadap sebagai berikut
r(v11∣∏O = (1,1,-,1,3,3,-,3,-,3,3,-,3),
r(υ21∣∏0 = (0,1,-,1,4,4,- ,4,-,4,4,∙∙*,4),
r(⅛∣W) = (1,1,-,1,4,4, ∙∙∙,4,-A4,-,4),
r(vJl∣M0 = (3,3,-,3,3,3,-,3,-,l,l,-,l), r(v^1 |W) = (4,4, - ,4,4,4, - ,4, - ,0,1, - ,1),
r⅛JW) = (4,4,-,4,4,4,-,4,-,l,l,-,l),
r(u∣U0 = (2,2,-,2,2,2,-,2,-,2,2,-,2).
Karena setiap vertex mempunyai representasi yang berbeda terhadap W, sehingga W merupakan himpunan pembeda.
ii) Akan ditunjukkan bahwa
dim(¾,,^,...^ ) ≥ ∑7=ιθi - 2)
Ditunjukkan dengan kontradiksi, andaikan adalah himpunan pembeda dari graf starbarbell dengan Jika dipilih himpunan dengan ,
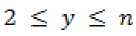
, dan
maka terdapat vertex

tasi
yang
sedemikian sehingga terdapat
represen-
sama
yaitu
. Hal ini
kontradiksi dengan pengandaian, sehingga
dim(5βm,,m,,.,π⅛ ) ≥ ∑Γ=ιOt - 2).
Dari i) dan ii), terbukti bahwa -.....l⅛^-" _ i-.= :1/". _-■■ □
Definisi dari edge corona dua buah graf diambil dari Hou and Shiu [7]. Graf adalah suatu graf yang diperoleh dari hasil operasi edge corona graf cycle dengan graf path dengan dan . Ilustrasi graf dapat dilihat pada
Gambar 2.

Gambar 2. Graf
Berikut ini diberikan hasil dimensi metrik pada graf .
Lema 3.3. Vertex dengan dan tidak termuat dalam basis
manapun pada graf .
BUKTI. Dibuktikan dengan kontradiksi. Andai P adalah basis pada graf yang memuat . Karena bukan basis, terdapat vertex^ EV(CmOPn)
sedemikian sehingga untuk setiap . Jelas bahwa
bukan basis, sehingga . Jika tidak berlaku dan
maka dan bukan basis pada graf .. Misal
diasumsikan dan tanpa mengurangi keumuman, adalah vertex . Pada
kasus ini, diperoleh untuk setiap . Artinya bukan
basis. Sehingga terbukti bahwa vertex dengan tidak termuat dalam
basis manapun. □
Teorema 3.4. Untuk setiap graf dengan dan berlaku
2,
3,
m = 3Vgenap (m > 4),n = 1;
m ganjil (m > 5),n = 1;
dim (Cm * Pn) = <
^2n 1
'2n — 2'
5
^2n — 21
m = 3,n > 2;
m > 3,n > 2.
BUKTI Pembuktian rumus umum dimensi metrik pada graf terbagi menjadi
empat kasus sebagai berikut.
Kasus 1. atau genap , .
-
1. Misalkan bilangan bulat, . Pilih , diperoleh
representasi semua vertex V( ) terhadap sebagai berikut
τ(u1∣W) = (1,2), r(u3∣W)= (2,1), τ(v12∣W) = (2,0), r(u2∣W)= (1,1), τ(v11∣W)= (0,2), τ(v13∣W)= (2,2).
-
2. Untuk m genap (m ≥ 4) dan n = 1.
Misalkan bilangan bulat genap . Pilih , diperoleh representasi semua vertex V( ) terhadap sebagai berikut


Dari 1 dan 2, setiap vertex V(
4) dan n = 1 memiliki representasi
himpunan pembeda dengan elemen.
) dan V( ) dengan m genap (m ≥ yang berbeda terhadap maka adalah Berdasarkan karakterisasi dari Chartrand et
al. [5] yang menyatakan jika dan hanya jika , karena
maka diperoleh dim( ) = 2. Hal ini berlaku pula untuk
'- ■: ? . dengan m genap (m ≥ 4) dan n = 1. □
Kasus 2. ganjil , .
Misalkan bilangan bulat, . Pilih , di-
terhadap sebagai
berikut
peroleh representasi semua vertex V( )
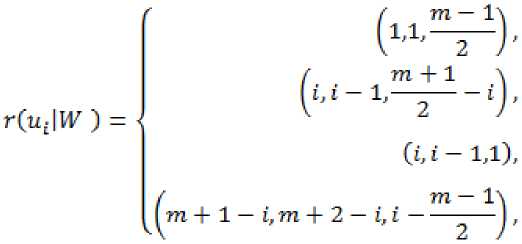
1. Untuk


2. Untuk m > 5.

Setiap vertexV(Crn<>Pjmemiliki representasi yang berbeda terhadap IV maka W adalah himpunan pembeda dengan 3 elemen. Selanjutnya ditunjukkan C m $ ^n tidak memiliki himpunan pembeda dengan - elemen. Andaikan ^m ^ ^n memiliki himpunan pembeda IV dengan - elemen, terdapat 3 kemungkinan pemilihan vertex dari IV . Akan tetapi, berdasarkan Lema 3.3 vertex ^ e vdcm) dengan 1 < i < m dan m > 3 tidak termuat dalam basis manapun sehingga w c ιz(ΛJ . Sehingga hanya ada 1 kemungkinan pemilihan vertex dari W yaitu kedua vertex dari W termasuk dalam {v™ : 1 ≤ m ≤ n} ⊂ V(P1)
Misalkan salah satu vertex dalam W adalah tfι dan vertex lainnya adalah L1 , dengan ( 2 < s < m ). Diperoleh representasi yang sama yaitu
;
m-ι∣^) r (7 ι I V∙ J (3,^ 2), s
;
m-
∣W) = (3,s-2),s=⅛≡ .
7 ' j 2 ; dan
r(u3∣W) = r(v11 W) = (2,m — s + 2),^-^
S s < m
.
, selalu diperoleh dua vertex
Untuk ^ - {vι»vι} , dengan 2 ≤ t < s :
^(cm<>Pn) yang memiliki representasi sama terhadap . Hal ini kontradiksi
dengan pengandaian. Diperoleh representasi yang sama terhadap . Oleh karena itu, tidak memiliki himpunan pembeda dengan elemen. Himpunan pembeda dengan kardinalitas minimum dari adalah elemen, sehingga terbukti
λ: ■:: L .. r. : = ?, untuk ': ganjil : ': ≤ = : dan - - -. □
Kasus 3. dan .
Graf dengan dan mempunyai himpunan vertex . Berdasarkan
Lema , vertex dengan dan tidak termuat dalam basis manapun sehingga . Pembuktian dibagi menjadi bagian yaitu untuk path dengan dan path dengan
-
1. Path dengan .
-
(a) Satu dari dua vertex
dengan merupakan elemen . Jika
vf, vf e W
maka
d0^ vq ) = dfevq) = 2
d(vf ^p) = dengan
dan
dan sehingga
. Dipilih vertex .
-
(b) Jika setiap vertex maka dan
. Sehingga salah satu dari ketiga vertex tersebut merupakan elemen . Misal dipilih , terdapat dua vertex dengan
representasi sama yaitu . Jika dipilih maka
. Sehingga , dipilih
.
-
(c) Dari (a) dan (b), jika himpunan pembeda maka setidaknya terdapat 2 elemen dari setiap 5 vertex. Tanpa mengurangi keumuman misal dipilih terdapat elemen . Jika dipilih maka diperoleh 2
pasang vertex dengan representasi berbeda terhadap sehingga vertex tese-
but merupakan elemen . Pada path , vertex dengan harus menambahkan vertex ke dalam elemen . Jika
maka
-
(d) .
Dari (a), (b), dan (c) diperoleh pengambilan dengan
P = 0,1, j r = 0,1,1 τ.1 , v2+5r^Γv"+1
dan . Jika terdapat atau

adalah
. Akibatnya kardinalitas pada path
maka elemen

-
2. Path dengan .
-
(a) Jika setiap vertex maka
.
Sehingga salah satu dari ketiga vertex tersebut adalah elemen . Misal dipilih , terdapat dua vertex dengan representasi sama yaitu
. Sama halnya jika dipilih maka
. Sehingga , dipilih .
(b) Jika setiap vertex maka . Sehingga salah
satu dari kedua vertex tersebut adalah elemen . Dipilih , terdapat
dua vertex dengan representasi sama yaitu
. Berarti
, sehingga dipilih
(c) Dari (a) dan (b), terdapat setidaknya 2 elemen himpunan pembeda dari setiap 5 vertex. Tanpa mengurangi keumuman misal dipilih terdapat
elemen . Jika dipilih . Diperoleh 2 pasang vertex
dengan representasi berbeda terhadap sehingga vertex tesebut merupakan elemen . Pada path , vertex dengan harus menambahkan vertex ke dalam elemen . Jika maka
r(<JW') = r(<,,r-2∣W')
Dari (a), (b), dan (c) diperoleh pengambilan dengan
P = 0,1,

adalah
—1 r = 1 2 — Γ-1 v3+5γξ^1 - vn+ι
dan . Jika terdapat atau
maka elemen . Akibatnya kardinalitas pada path

Dari 1 dan 2 berakibat kardinalitas dari adalah jumlahan dari kardinalitas pada
kedua path yaitu dan
2 1 i 2 j
. Diperoleh kardinalitas dari adalah . Se-
1. dim(C30P J = 2[-] + ∣-1
hingga r r untuk • - - -. □
Article DOI: 10.24843/JMAT.2020.v10.i01.p121
Kasus 4. dan .
Graf dengan dan mempunyai himpunan vertex
. Misal
dipilih suatu himpunan tak kosong . Analog dengan Kasus 3 poin 2, untuk
path dengan , diperoleh pula pengambilan dengan
dan . Jika terdapat atau
maka elemen . Terdapat copy graf pada .
5
[2n-2 1
Sebanyak vertex pada setiap copy dari graf merupakan elemen . Akibatnya
kardinalitas adalah
Γ2n-2 1 x n∖ Γ2π^
— αιm(Cm 0 =m —-
. Sehingga terbukti bahwa
untuk ':' ': : dan -. □
Berdasarkan hasil dan pembahasan di atas dapat disimpulkan bahwa dimensi metrik pada graf starbarbell adalah
dMSB"^,..,,^) = ^Oe ^ 2).
Dimensi metrik pada graf adalah
m = 3 V genap (m > 4),n = 1; m ganjil (m > 5),n = 1;
dim(cm β ⅞) = λ 2
m — 3,n > 2;
m > 3,n > 2.
Saran yang diberikan adalah untuk menentukan dimensi metrik pada kelas graf yang belum pernah diteliti, misalnya graf king dan hasil operasi edge corona pada graf path dan graf lengkap.
Ucapan Terima Kasih
Penulis mengucapkan terima kasih atas dukungan dana penelitian anggaran tahun 2019 dari Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sebelas Maret Surakarta, Indonesia.
Daftar Pustaka
-
[1] Ba cˇ a M, Baskoro E T, Salman A N M, Saputro S W and Suprijanti D, The
metric dimension of regular bipartite graphs, Bull. Math. Soc. Sci. Math. Rou-manie Tome 54, 15-28, 2011.
-
[2] Budianto W T and Kusmayadi T A, The local metric dimension of starbarbell graph, Km ⊙ Pn graph, and M¨obius ladder graph, J. Phys.: Conf. Ser. 1008, 012050, 2018.
-
[3] Caceres J, Hernando C, Mora M, Pelayo I M, Puertas M L and Seara C, On the metric dimension of some families of graphs, Electronic Notes in Discrete Math. 22, 129-133, 2005.
-
[4] Caceres J, Hernando C, Mora M, Pelayo I M and Puertas M L, On the metric dimension of infinite graphs, Electronic Notes in Discrete Math. 35, 1-17, 2009.
-
[5] Chartrand G, Eroh L, Johnson M and Oellermann O, Resolvability in graphs and the metric dimension of graph, Discrete Appl. Math 105, 98-113, 2000.
-
[6] Harary F and Melter R A, On the metric dimension of a graph, Ars Combina-toria 2, 191-195, 1976.
-
[7] Hou Y and Shiu W, The spectrum of the edge corona of two graphs, Electronic Journal of Linear Algebra 20, 586-594, 2010.
-
[8] Kusmayadi T A, Kuntari S, Fikri A F, Rahmadi D and Pradana H C, The metric dimension of sunflower, t-fold wheel, and K1 + (Pn ⊙ Pm), Far East Journal of Mathematical Sciences (FJMS) 99, 687-698, 2016.
-
[9] Slater P J, Dominating and reference sets in a graph, J. Math. Phys. Sci. 22, 445-455, 1988.
-
[10] Widodo B J, Kusmayadi T A and Kuntari S, Metric dimension of helm graph and double cones graph, AIP Conference Proceedings 1746, 020049, 2016.
43
Discussion and feedback