PEMODELAN ALJABAR MAX-PLUS DAN EVALUASI KINERJA JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK DENGAN KAPASITAS PENYANGGA TAKHINGGA

Jurnal Matematika, Vol. 1, No. 1, 2010, 8—15

PEMODELAN ALJABAR MAX-PLUS DAN EVALUASI KINERJA JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK DENGAN KAPASITAS PENYANGGA TAKHINGGA

¹M. ANDY RUDHITO, ²SRI WAHYUNI, ³ARI SUPARWANTO, DAN ⁴F. SUSILO

¹Mahasiswa S3 Matematika FMIPA UGM dan Staff Pengajar FKIP Universitas Sanata Dharma, Yogyakarta

^2,3Jurusan Matematika, FMIPA Universitas Gadjah Mada, Yogyakarta ⁴Jurusan Matematika, FST Universitas Sanata Dharma,Yogyakarta

Email : ¹[email protected], ²[email protected], ³[email protected], ⁴[email protected]

INTISARI

Makalah ini membahas tentang pemodelan dan penentuan waktu penyelesaian siklus (cycle) layanan jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga, dengan menggunakan aljabar max-plus. Hasil pembahasan menunjukkan bahwa dinamika jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga dapat dimodelkan ke dalam suatu persamaan matriks atas aljabar max-plus. Dapat ditunjukkan pula bahwa waktu siklus layanan jaringan antrian merupakan eigennilai max-plus dari matriks pada persamaan tersebut.dsfsdlkslkflskfslkflkflsdkfjlskflskjflsdlkjlklkl

Kata kunci: aljabar max-plus, eigennilai max-plus, jaringan antrian fork-join, waktu penyelesaian siklus layanan.

MAX-PLUS ALGEBRA MODELLING AND PERFORMANCE EVALUATION OF QUEUEING NONCYCLIC FORK-JOIN NETWORK WITH INFITE BUFFER CAPACITY

¹M. ANDY RUDHITO, ²SRI WAHYUNI, ³ARI SUPARWANTO, DAN ⁴F. SUSILO

¹PhD Students at Mathematics Department,FMIPA, UGM and Lecturer at FKIP, Sanata Dharma University, Yogyakarta

• ^2,3Mathematics Department, FMIPA, Gadjah Mada University, Yogyakarta

⁴Mathematics Department, FST, Sanata Dharma University,Yogyakarta

Email : ¹[email protected], ²[email protected], ³[email protected], ⁴[email protected]

ABSTRACT

This paper aims to model and determine the service cycle completion time of noncyclic fork-join queueing networks with infinite buffer capacity, using max-plus algebra. The finding show that the dynamics of the noncyclic fork-join queuing networks with infinite buffer capacity can be modeled into a matrix equation over max-plus algebra. We can also show that the service cycle completion time of queuing networks is a max-plus eigenvalues of the matrix in the equation.slklsklslsllsllllllllllllllllllllll

Keywords: max-plus algebra, max-plus eigenvalues, fork-join queueing networks, service cycle completion time.

• 1.    PENDAHULUAN

Jaringan fork-join merupakan salah satu sistem antrian yang memungkinkan pelanggan (customer) terpecah menjadi beberapa bagian, dan digabung kembali menjadi satu setelah pelanggan melalui sistem tersebut. Sistem seperti ini banyak dijumpai pada proses produksi dalam industri, pengiriman pesan dalam jaringan komunikasi, dan pemrosesan data dalam sistem komputer multiprosesor. Sebagai gambaran dalam jaringan komunikasi, pesan terpecah menjadi paket-paket yang disampaikan melalui jalur

terpisah, kemudian digabungkan kembali di titik tujuan jaringan tersebut hingga diperoleh pesan seperti semula.

Dalam pembahasan jaringan antrian dapat diasumsikan bahwa kapasitas penyangga (buffer) takhingga atau berhingga. Pemodelan dinamika jaringan dengan menggunakan aljabar max-plus dapat memberikan deskripsi yang lebih kompak dan terpadu (Baccelli et al., 1992). Di samping itu pemodelan ini juga memudahkan dalam hal komputasi numeriknya. Pemodelan jaringan antrian dengan menggunakan aljabar max-plus telah mulai

dibahas dalam Krivulin (1994, 1995, 1996a, 1996b). Dalam Krivulin (1994) telah dibahas pemodelan untuk antrian jenis G/G/1. Pemodelan dan evaluasi kinerja, yang meliputi waktu sistem pelanggan dan waktu tunggu pelanggan, untuk sistem antrian tandem telah dibahas dalam Krivulin (1995). Dalam literatur tersebut pembahasan secara eksplisit baru dibahas untuk sistem antrian tandem dengan kapasitas penyangga takhingga. Dalam Krivulin (1996a) untuk jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga telah diberikan persamaan dinamika keadaan (state dynamic equation) secara eksplisit, dan sistem antrian tandem dipandang sebagai kejadian khususnya. Persamaan keadaan dinamik secara eksplisit untuk jaringan antrian fork-join taksiklik dengan kapasitas penyangga berhingga telah diberikan dalam Krivulin (1996b). Pemodelan yang dilakukan dalam Krivulin (1996a, 1996b), diasumsikan bahwa pada waktu awal jaringan beroperasi, penyangga tidak selalu kosong.

Makalah ini akan membahas pemodelan dan kinerja (performance) jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga, dengan kondisi pada awal jaringan beroperasi, penyangga dalam keadaan kosong. Pemodelan dilakukan dengan pendekatan aljabar max-plus. Kinerja jaringan yang dibahas adalah analisis waktu penyelesaian siklus layanan jaringan antrian dikaitkan dengan eigennilaialjabar max-plus.

• 2.    ALJABAR MAX-PLUS DAN TEORI GRAF

Dalam bagian ini dibahas konsep dasar aljabar max-plus dan kaitannya dengan teori graf yang akan digunakan dalam pembahasan untuk bagian-bagian selanjutnya. Materi lebih lengkap dapat dilihat pada Baccelli et al. (1992), Krivulin (1996b), dan Rudhito (2003).

Diberikan Rε : = R ∪{ε } dengan R adalah himpunan semua bilangan real dan ε : = -∞. Pada R _ε didefinisikan operasi berikut: ∀a,b ∈ R_ε , a ⊕ b := max(a, b) dan a ⊗ b : = a + b. (Rε, ⊕, ⊗) merupakan semigelanggang komutatif idempoten dengan elemen netral ε = -∞ dan elemen satuan e = 0, yaitu bahwa ∀a,b ∈ R_ε berlaku:

• i)    a ⊕ b = b ⊕ a, (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c), a ⊕ ε = a.

• ii)    (a ⊗ b) ⊗ c = a ⊗ (b ⊗ c) , a ⊗ e = a + 0 = a = 0 + a = e ⊗ a.

• iii)    a ⊗ ε = ε ⊗ a .

• iv)    (a ⊕ b) ⊗ c = (a ⊗ c) ⊕ (b ⊗ c), a ⊗ (b ⊕ c) = (a ⊗ b) ⊕ (a ⊗ c).

• v)    a ⊗ b = b ⊗ a dan a ⊕ a = a.

Lebih lanjut (R_ε, ⊕, ⊗) merupakan semilapangan (semifield), yaitu bahwa (Rε, ⊕, ⊗) merupakan semigelanggang (semigelanggang) komutatif dengan kondisi untuk setiap a ∈ R terdapat -a sehingga berlaku a ⊗ (-a) = 0. Rmax : = (Rε, ⊕, ⊗) disebut dengan aljabar max-plus, yang selanjutnya cukup dituliskan dengan Rmax. Dalam hal urutan pengoperasian (jika tanda kurang tidak dituliskan), operasi ⊗ mempunyai prioritas yang lebih tinggi dari pada operasi ⊕. Pangkat k dari elemen x ∈ R dinotasikan dengan x^⊗ didefinisikan sebagai berikut:

0

x^⊗ : = 0

dan

_⊗k          _⊗k-1

x : = x ⊗ x ,

dan didefinisikan pula

0

ε^⊗ : = 0

dan

⊗^k

ε : = ε , untuk k = 1, 2, ....

Operasi ⊕ dan ⊗ pada Rmax di atas dapat

diperluas untuk operasi-operasi matriks dalam

R^m×n . Khususnya untuk matriks dalam R^n×n max                                                    max

didefinisikan

(A ⊕ B)ij = Aij ⊕ Bij dan

n

(A ⊗ B)ij = ⊕Aik⊗Bkj.

k=1

Didefinisikan matriks E ∈ R^n×n , max

(E )ij

dan matriks

0 , jika i = j ε , jika i ≠ j

ε ∈ R^mma^×xⁿ , (ε )ij := ε

untuk setiap i dan j . (Rⁿ_m^×_aⁿ_x , ⊕, ⊗) merupakan semigelanggang  (semiring) idempoten dengan

elemen netral matriks ε dan elemen satuan matriks E. Pangkat k dari matriks A ∈ Rⁿ_m^x_aⁿ_x dalam aljabar max-plus didefinisikan dengan A^⊗0 = En dan A^⊗k = A ⊗ A^⊗k-1 untuk k = 1, 2, .... Selanjutnya akibat sifat idempoten operasi ⊕, untuk setiap A ∈ R^nxn berlaku (E⊕A)^q = E ⊕ A ⊕ ... ⊕ A^q. max

Suatu graf berarah G didefinisikan sebagai suatu pasangan G = (V, A) dengan V adalah suatu himpunan berhingga takkosong yang anggotanya disebut titik dan A adalah suatu himpunan pasangan terurut titik-titik. Anggota A disebut busur. Suatu lintasan dalam graf berarah G adalah suatu barisan berhingga busur (i1, i2), (i2, i3), ... , (il-1, il) dengan (ik,

i_k+1) ∈ A untuk suatu l ∈ Ν (= himpunan semua bilangan asli), dan k = 1, 2, ... , l - 1. Untuk suatu lintasan ρ, panjang lintasan ρ didefinisikan sebagai banyak busur yang menyusun ρ dan dinotasikan dengan ρ_l . Suatu lintasan disebut sirkuit jika titik awal dan titik akhirnya sama. Sirkuit elementer adalah sirkuit yang titik-titiknya muncul tidak lebih dari sekali, kecuali titik awal yang muncul tepat dua kali. Suatu graf berarah G = (V, A) dengan V = {1, 2, , ... , n} dikatakan terhubung kuat jika untuk setiap i, j ∈ V , i ≠ j , terdapat suatu lintasan dari i ke j . Suatu graf yang memuat sirkuit disebut graf siklik, sedangkan suatu graf yang tidak memuat sirkuit disebut graf taksiklik.

Untuk setiap graf berarah G = (V, A) dengan n titik, didefinisikan suatu matriks G ∈ Rⁿ_m^×_aⁿ_x , yang disebut dengan matriks kedampingan dari graf berarah G , dengan unsur-unsurnya adalah

0, jika ( j,i) ∈ A;

.

ε, jika (j,i) ∉ A.

Gj = i

Diberikan graf berarah G = (V, A) dengan V = {1, 2, ... , p}. Graf berarah G dikatakan berbobot jika setiap busur (j, i) ∈ A dikawankan dengan suatu bilangan real A_ij. Bilangan real A_ij disebut bobot busur (j, i), dinotasikan dengan w(j, i). Dalam penyajiannya dengan gambar untuk graf berarah berbobot, busur diberi label dengan bobotnya. Didefinisikan graf preseden dari matriks A ∈ Rⁿ_m^×_aⁿ_x adalah graf berarah berbobot G(A) = (V, A) dengan V = {1, 2, ... , n}, A = {(j, i) | w(i, j) = Aij ≠ ε }. Perhatikan sebaliknya bahwa untuk setiap graf berarah berbobot G = (V, A) selalu dapat didefinisikan suatu matriks A ∈ Rⁿ_m^×_aⁿ_x , dengan

W j, i), jika (j, i) ∈ A ε, jika (j, i) ∉ A.

Aj = ‘

Jelas bahwa graf berarah berbobot tersebut merupakan graf preseden dari A.

Diberikan graf berarah berbobot G = (V, A) dengan V = {1, 2, ... , n}. Bobot suatu lintasan ρ = i1 → i₂ → ... → i_l didefinisikan sebagai jumlahan bobot busur-busur yang menyusun ρ . Bobot lintasan ρ dinotasikan dengan ρ_w . Untuk matriks A ∈ R^n×n , bobot suatu lintasan lintasan ρ = i → i → max

L → i_l dalam graf preseden G(A) adalah ρ_w =

A +A + L +A . Bobot rata-rata lintasan i 2 ^, i1         i 3 ^, i 2                     il^, il-1

ρ, dinotasikan dengan ρ , didefinisikan sebagai

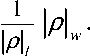
Berikut diberikan suatu interpretasi dalam teori graf untuk pangkat k matriks A ∈ Rⁿ_m^×_aⁿ_x dalam aljabar max-plus. Diberikan A∈ Rⁿ_m^×_aⁿ_x . Jika k ∈ Ν ,

maka unsur ke-st dari matriks A^⊗k adalah (A^⊗k )_st

= max (A + L +A +A ) = s ’ ik-1                             ¹2 ’ i1 i1 ’ t'

¹≤^k1^{, k}2 Lik-1 ≤ n

max ( A +A +

₁                            ,               i1, t          i 2, i1

¹≤^k1^,k2 Lik-1 ≤n

L +A ) untuk

s, ik-1 ⁷

setiap s^, t. Karena ( A₁t + Ai2, i₁+ ^l + ^Asi_k-₁) adalah bobot lintasan dengan panjang k dengan t sebagai titik awal dan s sebagai titik akhirnya dalam G(A), maka (A^⊗k )_st adalah bobot maksimum semua lintasan dalam G(A) dengan panjang k, dengan t sebagai titik awal dan s sebagai titik akhirnya. Jika tidak ada lintasan dengan panjang k dari t ke s, maka bobot maksimum didefinisikan sama dengan ε.

Sekarang diperhatikan bobot rata-rata maksimum sirkuit elementer, dengan maksimum diambil atas semua sirkuit elementer dalam graf. Diberikan A ∈ Rⁿ_m^×_aⁿ_x dengan graf presedennya G (A) = (V, E ). Bobot maksimum dari semua sirkuit dengan panjang k dengan titik i sebagai titik awal dan titik akhir dalam G(A) dituliskan sebagai (A^⊗k )_ii . Maksimum dari bobot maksimum semua sirkuit dengan panjang k dengan titik i sebagai titik awal dan titik akhir n_k dalam G(A) atas seluruh titik i adalah ⊕ (A^⊗ )_ii i=1

yang dapat dituliskan sebagai trace(A^⊗k ) dan rata-ratanya adalah (1/k)   trace(A^⊗k) . Kemudian

diambil maksimum atas sirkuit dengan panjang k ≤ n, yaitu atas semua sirkuit elementer, diperoleh suatu rumus untuk bobot rata-rata maksimum sirkuit elementer dalam G(A) (dinotasikan dengan λ_max(A)), n

sebagai berikut: λ_max(A) = ⊕_k=1 [(1/k) trace(A^⊗k ) ]_.

Suatu sirkuit dalam graf G disebut sirkuit kritis jika bobot rata-ratanya sama dengan bobot rata-rata maksimum sirkuit elementer dalam G. Suatu graf yang terdiri dari semua sirkuit kritis dari graf G disebut graf kritis dari G dan dinotasikan dengan G^c.

Berikut diberikan definisi dan teorema yang pembuktiannya dapat dilihat dalam Rudhito (2003).

Teorema 1. (Baccelli, et al., 2001). Diberikan A ∈ Rⁿ_m^×_aⁿ_x. Jika semua sirkuit dalam G(A) mempunyai bobot nonpositif, maka

∀p ≥ n , A^⊗p pm E ⊕ A ⊕L⊕ A^⊗n-1 .

Bukti : lihat Baccelli et al. (2001) atau Rudhito (2003).                            ■

Berdasarkan Teorema 1 di atas didefinisikan operasi bintang (∗) untuk matriks berikut ini.

Definisi 1. (Baccelli, et.al., 2001) Diberikan A ∈ Rⁿ_m^×_aⁿ_x dengan semua sirkuit dalam G(A) mempunyai bobot nonpositif . Didefinisikan n           n+1

A^* : = E ⊕ A ⊕ L ⊕ A ^⊗ ⊕ A ^⊗ ⊕ L dan

A⁺ : = A ⊗ A^*.

Definisi 2. (Eigennilai dan eigenvektor aljabar maxplus). Diberikan A ∈ Rⁿ_m^×_aⁿ_x . Skalar λ ∈ R_max disebut eigennilai aljabar max-plus matriks A jika terdapat suatu vektor v ∈ Rⁿ_max dengan v ≠ ε_n×1 sehingga A ⊗ v = λ ⊗ v. Vektor v tersebut disebut eigenvektor aljabar max-plus matriks A yang bersesuaian dengan λ.

Berikut teorema yang memberikan eksistensi eigennilai aljabar max-plus untuk setiap A ∈ Rⁿ_m^×_aⁿ_x .

Teorema 2. (Baccelli, et al., 2001). Diberikan A ∈Rⁿ_m^×_aⁿ_x . Skalar λmax(A), yaitu bobot rata-rata maksimum sirkuit elementer dalam G(A), merupakan suatu eigennilai aljabar max-plus matriks A.

Bukti:

lihat Baccelli, et al., (2001) atau Rudhito (2003).

■

Dalam Rudhito (2003) dijelaskan bahwa jika titik i menyusun busur dalam sirkuit kritis ρ0 dalam G(A) *

, maka kolom ke-i matriks B merupakan eigenvektor yang bersesuaian dengan eigennilai λmax(A), dengan B = -λmax(A) ⊗ A, dan B^* = E ⊕ B n -1

⊕ L ⊕ B^⊗ .

Berikut diberikan suatu teorema yang memberikan syarat perlu eigennilaialjabar max-plus suatu matriks.

Teorema 3. ( Baccelli, et.al., 2001) Diberikan A ∈Rⁿ_m^×_aⁿ_x . Jika skalar λ ∈ R, merupakan eigennilai aljabar max-plus matriks A, maka λ merupakan bobot rata-rata suatu sirkuit dalam G(A).

Bukti:

lihat Baccelli, et al. (2001) atau Rudhito (2003).

■

Dari Teorema 2 dan 3 dapat disimpulkan bahwa untuk A ∈ Rⁿ_m^×_aⁿ_x , λ_max(A) merupakan eigennilai aljabar max-plus maksimum matriks A. Berikut diberikan lema-lema yang akan melandasi pembahasan selanjutnya.

Lema 4. Jika A ∈ R ^n×n adalah matriks max

kedampingan graf berarah taksiklik G, maka A^⊗q = ε , untuk semua q > p, dengan p adalah panjang lintasan terpanjang dari G.

Bukti:

Perhatikan bahwa untuk matriks kedampingan di atas, unsur ke-st dari matriks A^⊗k adalah

^⊗k = max (A +A + L +A ), _st                                         i₁ , t          i₂ , i₁                        s, i_{k -1}

1≤i₁ ,i₂ ,Li_k-1≤n

untuk setiap s, t. Perhatikan bahwa (A^⊗k )_st ≠ ε jika dan hanya jika ada sedikitnya satu lintasan dengan panjang k, dengan s sebagai titik awal dan t sebagai titik akhirnya. Andaikan graf berarah di atas siklik, maka selalu dapat dibuat lintasan pada suatu sirkuitnya dengan panjang berapa pun. Hal ini berakibat bahwa A^⊗q ≠ ε , untuk semua q = 1, 2, .... Jadi jika graf berarah G di atas taksiklik, maka A^⊗q = ε , untuk semua q > p, dengan p adalah panjang lintasan terpanjangnya.                 ■

Lema 5. Diberikan A ∈ R^n×n dan b ∈Rⁿ dengan max             max

unsur-unsurnya positif atau sama dengan ε . Jika graf, dengan matriks A merupakan matriks kedampingannya, taksiklik, maka persamaan x = A ⊗ x ⊕ b mempunyai penyelesaian tunggal. Lebih lanjut penyelesaian diberikan oleh x = (E ⊕ A)^p ⊗ b, dengan p adalah panjang lintasan terpanjang dalam graf tersebut.

Bukti:

Dengan mensubstitusikan x pada persamaan di atas sebanyak q kali (q > p) diperoleh

Substitusi ke-1 :

x = A ⊗ (A ⊗ x ⊕ b ) ⊕ b

2

= A^⊗ ⊗ x ⊕ A ⊗ b ⊕ b

2

= A^⊗ ⊗ x ⊕ (E ⊕ A) ⊗ b.

Substitusi ke-2 :

x = A^⊗3⊗ x ⊕ (E ⊕ A ⊕A^⊗2) ⊗ b.

Substitusi ke-q :

x = A^⊗q+1 ⊗ x ⊕ (E ⊕ A ⊕L ⊕A^⊗q) ⊗ b. Mengingat graf di atas taksiklik maka A^⊗q = ε , untuk semua q > p, sehingga diperoleh

x = (E ⊕ A ⊕L⊕A^⊗p ) ⊗ b = (E ⊕ A)^p ⊗ b.

Dari proses mencari penentuan penyelesaian di atas nampak bahwa penyelesaian tersebut tunggal. ■

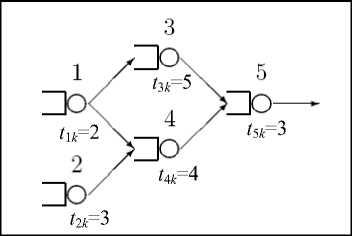
3. MODEL JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK

Dengan notasi aljabar max-plus persamaan (1) dan

(2) dapat dituliskan sebagai berikut

di(k) = tik ⊗ ai(k) ⊕ tik ⊗ di(k-1)

ai(k) =

© d j (k), jika P (i) ≠ φ, ^j P(i)

ε,        ,jika P (i) = φ.

Pengertian tentang jaringan antrian fork-joint berikut mengikuti dalam Krivulin (2000). Diperhatikan suatu jaringan dengan n titik pelayan tunggal (single-server) dan pelanggan kelas tunggal (single-class). Struktur jaringan antrian ini dapat dinyatakan dengan graf berarah taksiklik G = (N, A) dengan busur yang ditentukan oleh rute transisi pelanggan. Untuk setiap titik i ∈ N, didefinisikan himpunan pendahulu (predecessors) dan penerus (successors) titik i berturut-turut dengan P(i) = { j | (j, i) ∈ A ) dan S(i) = { j | (j, i) ∈ A ).

Untuk setiap titik i ∈ N terdiri dari sebuah pelayan dan penyangga dengan kapasitas takhingga yang bekerja dengan prinsip First-In First-Out (FIFO). Pada waktu-awal jaringan bekerja diasumsikan bahwa pelayan bebas pelanggan, penyangga untuk semua titik i dengan P(i) ≠ ∅ dalam keadaan kosong, sedangkan penyangga titik yang tidak mempunyai pendahulu (P(i) = ∅) mempunyai takhingga banyak pelanggan.

Operasi fork pada titik i diawali setiap kali layanan sebuah pelanggan selesai dan diperoleh beberapa pelanggan baru untuk antrian berikutnya. Banyaknya pelanggan baru yang muncul pada titik i sebanyak titik dalam S(i). Pelanggan-pelanggan baru ini secara serentak meninggalkan titik i dan menuju titik-titik j ∈ S(i) secara terpisah. Operasi join pada titik i terjadi saat pelanggan-pelanggan datang ke titik i , tidak hanya di menunggu di penyangga, tetapi juga menunggu sedikitnya satu pelanggan dari setiap titik j ∈ P(i) datang. Segera setelah pelanggan datang, bersama satu pelanggan dari setiap titik pendahulunya, mereka bersatu menjadi satu pelanggan dan masuk dalam penyangga dalam pelayan berikutnya. Dalam pengoperasian jaringan ini diasumsikan bahwa perpindahan pelanggan antar titik tidak memerlukan waktu.

Misalkan d(k) = [ d1(k) , d2(k), ... , dn(k)]^T , a1(k) , a2(k), ... , an(k)]^T dan

(3)

(4)

a(k) = [

Tk =

t1k

ε

ε

t

nk _

Persamaan (3) dan (4) di atas

menjadi

dapat dituliskan

d(k) = Tk ⊗ a(k) ⊕ Tk ⊗ d(k -1).

a(k) = G ⊗ d(k),

dengan matriks G yang unsur-unsur adalah

Gij = ^,

0, jika j∈ P(i) ; ε, untuk yang lain.

(5)

(6)

Perhatikan bahwa G merupakan matriks

kedampingan dari graf stuktur jaringan antrian. Dari persamaan (5) dan (6) dapat dituliskan persamaan

d(k) = Tk ⊗ G ⊗ d(k) ⊕ Tk ⊗ d(k -1).       (7)

Teorema 6. Diberikan jaringan antrian fork-join tak siklik dengan graf struktur jaringannya yang mempunyai panjang lintasan terpanjang p dan matriks kedampingan G. Persamaan keadaan eksplisit jaringan tersebut adalah

d(k) = A(k) ⊗ d(k -1), (8) dengan A(k) = (E ⊕ (Tk ⊗ G))^p ⊗ Tk .

Misalkan a_i(k) menyatakan waktu kedatangan pelanggan ke-k pada titik i, di(k) menyatakan waktu keberangkatan pelanggan ke-k pada titik i, dan tik menyatakan lama waktu layanan untuk pelanggan ke-k pada pelayan i. Diasumsikan jaringan mulai beroperasi pada nol waktu, yaitu bahwa di(0) = 0 dan

Bukti:

Dari hasil pada persamaan (7) dapat dituliskan d(k) = (Tk ⊗ G) ⊗ d(k) ⊕ (Tk ⊗ d(k -1)). Karena G adalah matriks kedampingan graf taksiklik dengan panjang lintasan p, maka menurut Lema 4, G^⊗q = ε untuk semua q > p. Akibatnya (T_k ⊗ G))^q = ε untuk semua q > p. Selanjutnya menurut Lema 5, persamaan ini mempunyai penyelesaian

d(k) = (E ⊕ (Tk ⊗ G))^p ⊗ (Tk ⊗ d(k -1))

= ((E ⊕ (Tk ⊗ G))^p ⊗ Tk ) ⊗ d(k -1)).

■

Contoh 1.

Jaringan antrian fork-join taksiklik dengan n = 5 diperlihatkan dalam Gambar 1 berikut.

di(k) = ε untuk semua k < 0, i = 1, ..., n. Dinamika

antrian pada titik i dapat dinyatakan dengan

di(k) = max(tik + ai(k), tik + di(k- 1)) ,

ai(k) =

max (d _j (k)), jika P(i) ≠ φ, < j ∈ P (i) j

ε,           jika P (i) = φ.

(1)

(2)

Gambar 1.

' d 1(2)'		' 2	ε	ε	ε	ε'		' 2'		' 4'
d 2(2)		ε	3	ε	ε	ε		3		6
d 3(2)	=	7	ε	5	ε	ε	®	7	=	12
d 4(2)		6	7	ε	4	ε		7		11
. d 5(2).		.10	10	8	7	3.		.10.		15

Dengan menggunakan program Matlab, diperoleh perhitungan hingga k = 30, seperti dalam Tabel 1 berikut.

Matriks kedampingan dari graf pada jaringan di atas adalah

	ε	ε	ε	ε	ε
	ε	ε	ε	ε	ε
G =	0	ε	ε	ε	ε
	0	0	ε	ε	ε
	.ε	ε	0	0	ε.

Nampak bahwa panjang lintasan terpanjangnya adalah p = 2. Dari persamaan (8) diperoleh persamaan keadaan

d(k) = A(k) ⊗ d(k -1) , dengan

A(k) = (E ⊕ (Tk ⊗ G))² ⊗ Tk

= (E ⊕ (Tk ⊗ G) ⊕ (Tk ⊗ G)²) ⊗ Tk

t1k	ε	ε	ε	ε
ε	t2k	ε	ε	ε
t1k ⊗t3k	ε	t3k	ε	ε
t1k ⊗t4k	t2k ⊗t4k	ε	t4k	ε
t1k⊗(t3k⊕t4k)⊗t5k	t2k ⊗t4k ⊗t5k	t3k ⊗t5k	t4k ⊗t5k	t5k.

Misalkan lama waktu layanan untuk pelanggan ke-k pada pelayan i adalah sebagai berikut: t_1k = 2, t_2k = 3, t3k = 5, t4k = 4 dan t5k = 3, maka diperoleh

	’ 2	ε	ε	ε	ε
	ε	3	ε	ε	ε
A(k) =	7	ε	5	ε	ε
	6	7	ε	4	ε
	.10	10	8	7	3

Sehingga untuk k = 1, 2 diperoleh

’ d 1(1)'		’ 2	ε	ε	ε	ε ’		'0'		' 2'
d 2(1)		ε	3	ε	ε	ε		0		3
d 3(1)	=	7	ε	5	ε	ε	®	0	=	7
d 4(1)		6	7	ε	4	ε		0		7
. d 5(1).		.10	10	8	7	3.		.0.		.10.

• 4.    EVALUASI KINERJA JARINGAN ANTRIAN

Diperhatikan waktu penuntasan siklus layanan jaringan sebagai barisan siklus layanan: siklus kepertama mulai saat waktu awal, dan berakhir segera setelah semua pelayan dalam jaringan menuntaskan layanan kepertamanya, siklus kedua berakhir segera setelah semua pelayan dalam jaringan menuntaskan layanan keduanya, dan seterusnya. Dengan demikan waktu penuntasan siklus ke-k pada titik i adalah d_i (k) , sehingga waktu penuntasan siklus ke-k pada jaringan dapat dinyatakan sebagai

maxd_i (k)

i

dengan d_i(0) = 0, i = 1, ..., n dan k = 0, 1, 2, ....

Selanjutnya waktu siklus layanan jaringan dapat dinyatakan dengan:

γ = lim max(d_i (k)) .

k→∞ k i

Contoh 2:

Dari hasil dalam Contoh 1 pada Tabel 1 nampak bahwa waktu penuntasan siklus ke-k dari jaringan tersebut adalah d₅(k). Perhitungan secara numerik mengenai γ dari Contoh 1, diperoleh hasil seperti dalam Tabel 2 berikut.

Nampak dalam contoh ini bahwa nilai

γ = lim max(d_i (k)) k→∞ k i

= lim ¹(d₅(k)) = 5. k→∞ k

Dengan menggunakan program Matlab dapat ditentukan bahwa eigennilai aljabar max-plus maksimum matriks A adalah λmax(A) = 5 dan eigenvektor yang bersesuaian adalah [ε ε 0 ε 3]^T .

Secara umum sifat yang muncul pada contoh-contoh di atas diberikan dalam teorema berikut ini.

Teorema 7. Jaringan antrian fork-join taksiklik kapasitas penyangga takhingga, dengan persamaan keadaan eksplisit jaringan tersebut adalah d(k) =

A(k) ⊗ d(k -1), k = 1, 2, ..., mempunyai waktu penuntasan siklus layanan

γ = lim 1 max(d_i (k)) = λmax(A(k)), k→∞ k i

yaitu eigennilai max-plus maksimum matriks A(k) tersebut.

Bukti:

Perhatikan bahwa

d(k) = A(k) ⊗ d(k -1)

= (A(k) ⊗ A(k-1)⊗ … ⊗A(2) ⊗ A(1)) ⊗ d(0).

Karena dalam tulisan ini diasumsikan bahwa

A(1) = A(2) = ... = A(k)

dan d(0) = 0, maka d(k) = A^⊗k ⊗ 0 , sehingga di(k) = ma_jx [(A^⊗k)_ij]

dan

maxd_i (k) = max { max [( A^⊗k_ij )]}. i     ij

Bobot rata-rata maksimum sirkuit elementer dalam graf presede_nn matriks A tersebut λmax(A) = ⊕((1/k) trace(A^⊗k) ) , k=1

Selanjutnya diperoleh bahwa

di(k) =max [(A^⊗k) ] = max (λ (A))^⊗k _j                      ij _j

sehingga

maxd_i (k) = max (max ( (λ_max (A))^⊗k ) i     ij

=(λmax(A))^⊗k .

Dengan demikian diperoleh bahwa

γ = lim max(d_i(k)) k→∞ k i

= lim ¹ (λmax (A))^⊗k k→∞ k

= lim¹ (kλmax(A)) = λmax(A). k→∞ k

■

yang merupakan eigennilai aljabar max-plus maksimum matriks A. Oleh karena itu berlaku

A^⊗k⊗ v^*= (λmax(A))^⊗k⊗ v^* ,

untuk suatu eigenvektor v^*. Hal ini berakibat ma_jx((A^⊗k)_ij⊗ vj^*) = (λ_max(A))^⊗k ⊗ma_jx(v^*_j) , dengan max (v^* ) ≠ ε . Vektor - max (v^* ) ⊗ v^* juga j^j                                    j^j

merupakan eigenvektor yang berkaitan dengan eigenvektor λmax(A) di atas, dengan

- max (v^* ) ⊗ max (v^* ) = 0.

j^j j^j

Tabel 1. Hasil Perhitungan d(k)

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d1	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
d2	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
d3	7	12	17	22	27	32	37	42	47	52	57	62	67	72	77
d4	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
k	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
d1	32	34	36	38	40	42	44	46	48	50	52	54	56	58	60
d2	48	51	54	57	60	63	66	69	72	75	78	81	84	87	90
d3	82	87	92	97	102	107	112	117	122	127	132	142	147	152	157
d4	67	71	75	79	83	87	91	95	99	103	107	111	115	119	123
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155

Tabel 2. Hasil Perhitungan γ

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
d5/k	10	7,5	6,67	6,25	6,00	5,83	5,71	5,63	5,56	5,50	5,45	5,42	5,38	5,36	5,33
k	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155
d5/k	5,11	5,11	5,11	5,10	5,10	5,10	5,10	5,10	5,09	5,09	5,09	5,09	5,09	5,09	5,08

DAFTAR PUSTAKA

Bacelli, F., et al. 1992. Synchronization and Linearity. New York: John Wiley & Sons.

Krivulin, N.K., 1994. Using Max-Algebra Linear Models in the Representation of Queueing Systems. Proc. 5^th SIAM Conf. on Applied Linear Algebra, Snowbird, AT. June 15-18, 1994. 155—160.

Krivulin, N.K., 1995. A Max-Algebra Approach to Modeling and Simulation of Tandem Queueing Systems. Mathematical and Computer Modelling. 22(3):25—31.

Krivulin, N.K., 1996a. The Max-Plus Algebra Approach in Modelling of Queueing Networks Proc. 1996 SCS Summer Computer Simulation Conference (SCSC-96). July 2125. The Society for Computer Simulation, 485—490.

Krivulin, N.K., 1996b. Max-Plus Algebra Models of Queueing Networks. Proc. Intern. Workshop WODES’96 Univ. of Edinburgh, UK. Aug. 19-21, 1996. IEEE: London. 76—81.

Krivulin, N.K., 2000. Algebraic Modelling and Performance Evaluation, of Acyclic ForkJoin Queueing Networks. Advances in Stochastic Simulation Methods. Birkhauser. Boston. 63—81 .

Rudhito, Andy. 2003. Sistem Linear Max-Plus Waktu-Invariant. Tesis Magister Matematika Program Pascasarjana Universitas Gadjah Mada. Yogyakarta.