BY MEANS OF LINDEBERG’S CENTRAL LIMIT THEOREM

Written by WAYAN SOMAYASA
on November 09, 2021

Jurnal Matematika, Vol. 1, No. 1, 2010, 1—7

CONSTRUCTION OF A h -GENERALIZED STANDARD BROWNIAN SHEET BY MEANS OF LINDEBERG’S CENTRAL LIMIT THEOREM

WAYAN SOMAYASA

Jurusan Matematika, FMIPA, Universitas Haluoleo Kendari 93232 Email: [email protected]

ABSTRACT

We study the construction of a version of standard Brownian sheet called h -generalized standard Brownian sheet. It is shown by means of Lindeberg’s theorem that it is a limit process of a sequence of partial sums processes of independent random variables in the sense of weak convergence in the metric space of continuous functions on the compact region [0,1]×[0,1]. Based on this convergence we approximate by simulation the quantiles of Kolmogorov, Kolmogorov-Smirnov and Cramér-von Mises type statistics which are defined as continuous functionals of the process.

Keywords: h -generalized standard Brownian sheet, weak convergence, model-check, tightness.

1. INTRODUCTION

Let (Ω,Γ,Ρ) be a probability space, C(I) be the set of continuous functions on the compact set I := [θ,1]× [θ,1]⊂ ^² and B_c(I) be the Borel-σ algebra over C(I) with respect to the uniform topology, i.e., a topology generated by the supremum ^norm HL^{, where for}^f ∈ ^c⁽I) II^fIL := sup I f (t, s )∣. For any (t, s) ∈ I, the mapping (t, S )∈ I

^π(t,s)^: C⁽ⁱ) →^ defined by ^π(t,s)⁽^f ):= ^f⁽t^, s)^,f ∈ C(I) is called a natural projection.

Definition 1. Let h : I →¾>₀ be a function which has bounded variation in the sense of Vitali. A Gaussian process {B_h (t, s) : (t, s) ∈ I} induced by a random function B_h : Ω → C(I) in the sense of B_h(t,s;ω) = (∏_ts) °B_h)(ω) for every ω∈ Ω and (t, s) ∈ I, is called a h -generalized standard Brownian sheet if it satisfies the following conditions:

1. B_h (t, s) = 0 almost surely (a.s.) if t = 0 or s = 0 .
2. For every (t, s) ∈ I, E(B_h (t, s)) = 0 .
3. For any (t₁,s₁), (1₂,s₂) ∈ I,

E (Bh (11, si ) B_h (12, s 2)) = ∫ h (x, y )λ₁ (dx, dy ),

[0,11 ∧12 ]×[0,s 1 ∧s2 ]

where λI is the Lebesgue measure on I and x ∧ y is the minimum between x and y. Furthermore, let

U :=[t1,1₂ ]×[s₁, s₂ ]⊂ I, t₁ < 1₂ and s₁ < s₂ be a rectangle in I , the increment of this process over U is defined by

^δ U^Bh

:= ^Bh ⁽¹2 , s2 ) ^-^Bh ⁽¹2, ^s1) ^-^Bh ⁽^t1, s2) ⁺^Bh ⁽^t1, s1) ^.

We note that in the case of h is a constant function, we get standard Brownian Sheet whose existence was studied extensively by Kuelbs (1968) and Park (1971).

Remark 1. Under condition 1, conditions 2 and 3 are equivalent to the following two conditions. For any U := [t ₁,1₂ ]×[s₁, s₂ ]⊂ I, t₁ < 1₂ and s₁ < s₂,

^δ U^Bh

~

Ν 0, ∫ h(x, y)λ₁ (dx, dy)

k u )

For any family of rectangles

Uj := [t/-1,t_i]× Isj-1,s_j ^]:1 ≤ i ≤ m, 1 ≤ j ≤ q^}

in I, where 0 ≤ 10 < ^ < t_m ≤ 1 and

0 ≤ s0 < l < sq ≤ 1, it holds:

P ^

ω∈ Ω: ∆

U_ij

mq

∏ ∏ P

i=1j=1

Bh (ω) ≤ αij, 1 ≤ i ≤ m, 1 ≤ j ≤ q * =

ω∈

Ω : ∆_τ. B. (ω) ≤ α .>

Uij h i ∫

, αij ∈ ^.

In addition, let

{U^λ — [ti-1 + β,t + β]×[s j-i + Λs_j + λ] :1 ≤ i ≤ m, 1 ≤ j ≤ q} , where β and λ are any positive numbers such that t_m + β ≤ 1 and s_a + λ ≤ 1.

mq

Then the vectors (∆U 11 Bh,...,∆U Bh 'T and (∆ _fβλ Bh, k , ∆ _fβλ Bh T have mq - variate normal

U₁₁ U_mq

distribution with zero mean vector and variance-

covariance matrices are given by

diag ∫ h dλI,κ, ∫h dλI

V U11 Umq J

and

diag ∫ h dλι,κ, ∫h dλι ,

V U■■ ^!m J

respectively. Consequently, in contrast to the standard Brownian sheet, the process {Bh (t, s ): (t, s )∈ I} does not constitute a process

with stationary increments having sample paths in C(I).

In the future the continuous functional of the h -generalized standard Brownian sheet such as

K := sup B_h (t, s), 0≤t, s ≤1 ^h

KS := sup ∣B. (t, s)∣, 0≤t, s≤1^l^{h 1}

or

CR := ∫ B2(x, y)λ (dx,dy)

_Ih I

take important role in establishing asymptotic modelcheck or change-point problems for heteroscedastic spatial linear model, see MacNeill et al. (1994) and Somayasa (2007).

For a fixed natural number n , let ¾ⁿ×ⁿ be the space of n × n real matrices. The linear operator T_n : ¾ⁿ×ⁿ — C(I), such that for every matrix

ⁿ, ⁿ Wⁿ×ⁿ

An × n = ⁽a lk ⅞=1, k=1 ∈^λ^,

[ns] [nt]

^Tn⁽An×n⁾⁽^t,^s) ^:= ∑ ∑ an⁺k = 1 £ = 1 ^l k

( ^[^ns^] ∕ Γ ^nt^]

(^nt^{- [}^nt J) ∑ a[nt_]+i,k + (^ns^{- [}^nsJ) ∑ aL,[ns_]+i

k1 L 1

⁺ (nt^{- [}nt^])(ns ^{- [}ns^]⁾a[nt_h,[n+1,⁽t, s) ∈ I is called the partial-sums operator, where [x] := max{n ∈ Z : n ≤ x}. In this case we set T_n (A_n × _n)(t, s) = 0, if t = 0 or s = 0. Let En×_n = (^Lk )n=n k=1 ∈ ^n×n be a random matrix defined on the space (Ω,Γ,Ρ) whose components are mutually independent with E(ε_t_k ) = 0 and var(ε_k) = h(L / n, k / n), 1 ≤ L, k ≤ n. By means of

T_n , MacNeill et al. (1994) and Somayasa (2007) embedded the sequence (E_n × _n) _n ≥₁ into a sequence of stochastic processes { T_n (E_n×_n)(t, s): (t, s) ∈ I}_n≥1 defined on (Ω, Γ, Ρ). Thus, for every n ≥ 1, { T_n (E_n×_n)(t, s): (t, s) ∈ I} is induced by the random function T_n (E_n×_n): Ω — C(I). It was stated (without proof) in MacNeill et al. (1994) that for n →∞,

^{ Tfi⁽^En×n⁾⁽^t,^s)^{: (t},^s) ∈ ⁱ^} →

n m ≥1

{Bh (t, s): (t, s) ∈ I}.

Here, the notation —DD—→ stands for the convergence in distribution in the sense of Billingsley (1999), p. 20—22. The object of this paper is to show this convergence result.

2. TIGHTNESS IN C(I)

Let Ξ be a metric space and B_ξ be the Borel σ-algebra over Ξ . A sequence of probability measures (P_n) _n ≥₁ on a measurable space (Ξ, B_ξ ) is said to be tight, if and only if for every η> 0 there exists a compact subset K ⊂ Ξ , such that P_n(K) ≥ 1 -η, ∀ n ≥ 1. Correspondingly, a sequence of random functions (X_n) _n ≥₁ : Ω —Ξ is tight, if and only if the sequence of their distributions is tight.

We refer the reader to Park (1971) for the proof of the following result.

Theorem 1. Let {X_n(t,s): (t,s)∈ T c¾²}_n≥₁ be a sequence of stochastic processes induced by a sequence of random functions (X_n) _n ≥₁ : Ω — Ξ and {X (t, s ): (t,s)∈ T c¾²} be a stochastic process induced by a random function X : Ω — Ξ. Then

{Xn(t,s): (t,s)∈ T c¾²}n≥1 ———

{X(t,s) : (t,s)∈ T ⊂ ^²} for n — ∞, if ( Xn) n ≥1 is tight and if the sequence of finite

dimensional distributions of ( X_n )_n_≥₁ converges weakly to those of X, for n — ∞.

The modulus of continuity of a function f ∈ C(I) is defined as a function

Wf : (0,1) — ^≥₀, such that for every δ ∈ (0,1), Wf (^δ):= sup ∣^f (t 1^,^s1) ^-^f (t 2^, s 2)∣, where Il (t1,s1)-( 12, s 2)∣∣≤δ

U∙∣∣ is the Euclidean norm. For a fixed δ ∈ (0,1), Wf (δ) can be regarded as a continuous function of

f ∈ C(I) denoted by W(f, δ) . Hence, it is measurable on C(I) .

The following theorem reduces the tightness condition of Theorem 2.1 into a more simple one. The proof is presented in Somayasa (2007), p. 123— 124, in which a generalization of the result due to Theorem 3.1 in Billingsley (1999) was made from one to higher dimensional situation.

Theorem 2. Let {Xn (t, s): (t,s) ∈ I}_n≥₁ be a sequence of stochastic processes induced by a sequence of random functions (X_n) _n≥₁ : Ω → C(I) and {X (t, s): (t, s) ∈ I} be a stochastic process induced by a random function X : Ω→ C(I). jffor finitely many distinct points (t₁,s₁),l,(t_p,sq) ∈ I, p, q ∈ Ν,

(^x, ⁽11^,^si),^l, ^x, ⁽tp, s, ))T≥₁

—→(X (t1, s1),l, X (tp, sq ))^t

as n → ∞, and for every ε > 0, lim limsup P{ω∈ Ω : W(X_n (ω), δ) ≥ ε}= 0, then ^δ→⁰ n →∞

for n →∞, {Xn(t,s):(t,s)∈ T c¾²}n≥₁ —-→ {X(t, s): (t,s) ∈ T c¾²}.

3. MAIN RESULT

In what follows we present and proof the theorem stated in MacNeill et al. (1994) by means of the Lindeberg’s central limit theorem.

Theorem 3. Let E_n×_n = (ε^k )n=n k=1 ∈ ^ⁿ×ⁿ be a random matrix defined on the space (Ω, Γ, Ρ) whose components are mutually independent with E (εt k ) = 0 and var(ε_t_k ) = h (t / n, k / n),

1 ≤ t, k ≤ n, where h: I → ¾>₀ is a function which

has bounded variation in the sense of Vitali on I.

Then, for n → ∞,

^{¹ Tn⁽En×n⁾⁽^t^,^s^{): (}^t,s) ∈ I^}^—→

n m ≥1

{B_h (t, s): (t, s) ∈ I}.

Proof:

We shall proof this theorem by showing that ^{ nTn⁽En×n⁾⁽^t^,^s)^: (^{t, s}) ∈ ⁱ^}n≥1 satisfies the

sufficient conditions of Theorem 2.2, i.e., for any

choice of distinct points (t₁,s₁),l,(t_p,s_q) ∈ I,

(1 T, (En × n)(t1, s1), l , t Tn (En × n Xtp, s, ))^t ——→

⁽^Bh⁽t1^,^s1⅛^,^l^, B₁ (tp^,^s, ))^r,

and

lLm^limsuP P{^ω∈ ^ω^: W(nT⁽En×n (ω))^,δ) ≥ ^ε}= ⁰

^δ→⁰ n →∞

, for every ε > 0 . For the first condition, let us

consider a single point (t, s) ∈ I, by the definition,

we have n Tn (En × n)(t^, s)=n S _t nt ][ ns ]+n ψn, _t, s^, where ^ψn_jjs ^:= ⁽^nt-[n^tDk∑1'^ε[nt +1,k ⁺

[nt]

⁽ns ^-[nsJ)∑1^εL,[n]+1 ⁺

⁽nt ^-[ nt^]⁾⁽ns ^-[ns ∣>^ε n+1,[ns ]+1

[ns ] [nt]

^and S[nt][ns ] := ∑ ∑ ^εtk. By ^{the stro}ng ^{law of} large k=1 t=1

number, it holds 1ψ,,_t, ———→ 0, for n → ∞ . n n,t,s

Furthermore, let

[ns] [nt]

Bn^{2 :}= ^var⁽S[ nt ][ ns ])= Σ Σ ^h⁽^t / ⁿ^,^k / ⁿ ).

k=1 t=1

Since lim B_n = ∞, then for every ε > 0,

n →∞

lim L (ε) = 0 , where n →∞

[ ns ] [ nt ]

L(ε):= -it∑ ∑ ∫∣^²P^ε∙(dx)

n^k=¹^t=¹ {x∣≥B }

and P^ε^t^k is the distribution of ε_t_k on ¾ . Hence, by the Lindeberg’s central limit theorem and Slutsky’s theorem, we get

t

¹

n ^j[nt][ns]

D

÷ Ν 0, ∫ h d^ , I [0, t M0, s ]

for n → ∞ . This together with the preceding results imply

iT_n (En × n)(t, s ) —-

(^

÷ Ν 0, ∫ h dλ₁

L [0,t]×[0,s]

which is the distribution of B_h(t, s) .

Consider now any two distinct points (t₁, s₁) and (1₂, s₂) in I. Suppose first that t₁ < 1₂ and s₁ < s₂. We are to prove that for n → ∞,

⁽¹^Tn ⁽^En×n ⁾⁽^t1^,^s1), I ^Tn ⁽^En×n ⁾⁽¹2^, s2) ⁾^T

——→⁽B_h (t1, s1), B_h (12, s 2)⁾^Twhich follow by the analogous argument to the single point case, if for n → ∞,

p, q ∈ Ν, it holds

(n S[nt 1 ][ns 1 ]^, n ^S[nt2 ][ns2 ]

D

(

÷ Ν 0,

I I

∖ (

∫ h dλ , Ν 0, [0,11 ]×[0, s 1 ] J [

∫ h dλ

^[0,¹2 ]×[⁰,^s2 ^] JJ

Since

⁽ n ^S [ nt i ][ ns ₁ ]^, n ^S[ nt 2 ][ ns 2 ]f =

(n ^S[nt ₁ ][ns₁ ]^, n ^S[nt2 ][ns2 ] n ^S[nt ₁ ][ns₁ ] ⁺ n ^S[nt ₁ ][ns ₁ ]) ^,

where nS[nt 1 ][ns 1 ] ^and nS[nt2 ][ns2 ]^- nS[ ₁₁11 ][ns 1 ] are mutually independent, then by the Cramér-Wald technique (Billingsley, 1995, p. 382), for n →∞

11 1^T

∖n ^j[nt][nsj^, n ^j[nt₂][ns₂] n ^a[nt₁][ns₁↑)

r /

∖

∕

—— Ν 0, ∫ h cL⅜ , Ν 0, ∫ h dλI - ∫ h dλ .

Pw(1 T. (En×,),δ2) ≥ 3ε}

qp

≤∑ ∑Pl sup∣nTn(E×)(t■s)-.T(e..)(t«>sk-1)≥ε∖

k=1 H [(^t^,^s )Utk J

whenever min (t_e -1_t_-₁) ≥ δ, min (s_k - s_k_-₁) ≥ δ, 1<t<p 1<k<q

for δ > 0 . Let us chose for 0 ≤ £ ≤ p and

0 ≤ k ≤ q, 1₁ := m_e / n and s_k := m_k∕ n, where m_e

'

and m_k are integers that satisfy the conditions

0 = m_r. < m. < l < _m < _m < . < _m = n, 0 1 £ -1 ^t p

'' ' ' '

0 = m „ < m, < l < m„ , < m„ < ... < m = n .

0 1 L -1 L q

Then by the definition of partial sums, we get

p ¹W (.Tn (E,×. ),δ2) ≥ 3ε}

V

V [0,t⅛, sj J

V [o, 12 Mo, s 2 ] [0,t⅛, sj

Hence, by applying by the Cramér-Wald technique once again to the right hand side of the last equality, for n → ∞ we get

⁽n ^S[nt ₁ ][ns ₁ ]^, n ^S[nt₂ ][ns₂ ] n ^S[nt ₁ ][ns ₁ ] ⁺ n ^S[nt ₁ ][ns ₁ ] Z --DD→

qp

≤ ∑∑ ^P∖

k=1 t=1

max

^mt-1≤ ⁱ1≤ ^m t mt-1≤ i₂≤ mt

Si1i2

- S

mt-1mk-1

^,≥ ε n >

r r

∖

Ν 0, ∫ h dλI , Ν 0, ∫ h dλ - ∫ h dλ_ι + ∫ h dλI

_v V ∣^0,^t1M⁰^s1] J

V [0,t2⅛ s 2]

[0, t⅛ sj [0t1]×0,sj

= Ν 0, ∫ h dλ , Ν 0, ∫ h dλ .

_v V [0,t1M0, sj J

The result follows since

V ^[^o,¹2 W⁰,^s 2 ]

whenever m_e / n - m_t_-₁ / n ≥ δ and

m_l /n - m_l_-₁ /n ≥ δ, for 1 < t < p and 1 < k < q , kl

where S_t_k := . ∑ ∑ εi_j . But by the independence j=1 i=1

of {fj :1 ≤ i, j ≤ n}, we further get

pW (.T, (E×, ),δ2) ≥ 3ε}

q p ...

≤V VP^ max S₁₁ ≥εn∖

⅛ I=T 0≤ⁱ1≤(^mt^-^mt-1) ¹2^l

C

∕

Ν 0, ∫ h dλI , Ν 0, ∫ h dλI

V

has the

V [0,t1]×[0, sj j

V

same distribution

[0,12 ]×[0, s 2 ] J_j

with the

(B_h(t1,s1),B_h(1₂,s₂))T . The other cases handled analogously. Thus the assertion

vector can be for two

points follows. The set of three or more points can be treated in the same way, and hence the finite dimensional distributions of

^{¹ Tn⁽En×n⁾⁽^t^,^s^{): (t,s)} ∈ I} n ^jn ≥1

converges properly.

To prove the second condition we apply the following auxiliary result. For any family of rectangles

For further simplification we chose m_e := tm and m_k := km' for some integers m and m' that satisfy m_t - m_t_-₁ = m ≥ nδ and m_k - m_k_-₁ = m'≥ nδ, for 0 ≤ t < p and 0 ≤ k < q . Since the indexes p and q must satisfy ( p - 1)m < n ≤ pm and (q -1)m' < n ≤ pm', we chose

p := Pn / m ∖ —ⁿ— — 1/ δ < 2 / δ and q := Pn / m'∖ ———→ 1/ δ < 2 / δ. Moreover, since

n/m ———→1/δ > 1∕2δ

and n∕m' ————— 1/δ > 1∕2δ, then for every ε > 0 and large n, we have

Uj := [t-1, t_i ]× Isj-1, sj^] :1 ≤ i ≤ p, 1 ≤ j ≤ q^} in

I

and ε > 0 ,

where 0 = 10 < ^ < tp = 1,

0 = s0 < L < _Sq = 1, it holds:

P{W(¹nTn(En×n),δ 2) ≥3ε}

≤ P maxS δ2 0≤l≤m ^lk

0≤ k ≤ m'

max P{ S ≥ ^λ^mm^' } is

0≤l≤m ^lk 3

0≤k ≤m'

dominated

by

max<

∫ 9 h dλ

[0,t]×[0,s]

λ² n²

9M λ²

. 10λ _D\ . r—I

≤ P max S ≥ λ mm'

2 0≤l≤m ^lk

[θ≤k≤ m'

≤ 48^λ² max P{ S ≥ ^λ^mm^' }

ε2 0≤l≤m ^lk 3

0≤k≤m'

which directly implies that

lim lim sup ⁴⁸ max P{ S ≥ ^λⁿ }

λ→∞ n_→∞ ε2 0≤l≤n ^lk 3

0≤k≤n

where λ:= ε/ 2δ. The last inequality follows from Etemadi’s inequality (Billingsley, 1995, Theorem 22.5). Thus the second condition will follow if we can show that

limlimsup max P{ S ≥ ^λ^mm^'}=0,

λ→∞ ε2 0≤l≤m ^lk 3

^m^,^m^→ 0≤k ≤m'

which is the same with the condition

limlimsup max P{ S ≥ ^λⁿ } = 0 .

^λ^→∞ m,m'→∞ ε^{2 0}^≤^l^≤^m^l^k³

^m^,^m^→ 0≤k ≤m'

By the Lindeberg’s central limit theorem and Chebyshev’s inequality, if l_λ and k_λ are large enough such that l_λ ≤ l ≤ n and k_λ ≤ k ≤ n , then we have

[ ∫9hdλ

≤ lim limsup max ^[^0,^t^]×[^0,^s^]

ε²λ→∞ n→∞ λ n²

9M λ²

=0 This complete the proof of the theorem. ■

Corollary 1. Let (Ξ, d) be a metric space with metric d , and let B be the Borel σ -algebra over

B . If g : C(I) → Ξ is continuous on C(I) , then

g fa (e En × n)) ——→ g (b Bh),

as n → ∞ .

p { Ss, k∣ ≥ ■}≤ p •

kl

∑ ∑εj_l

j =1 i =1

= P. ∣Ν(0,1)∣ ≥

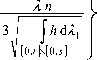
λn

≥₃

However the continuity assumption on g can be

weakened as follows. Let D ∈ B be the set of ^g C(I)

discontinuity points of g and let W be the

probability measure of B_h on (C(I), B_C₍_I₎) . If g is

∫ 9 h dλ

[0,t]×[0,s]

≤ ₂₂ ,

λ n

measurable and W(D_g ) = 0, then

g(fa⁽^En×n)) ^——→g⁽^B_h)^{, as}ⁿ → ∞ .

for ^l^-¹ < t < ^l and ^k^-¹ < s < ^k , whereas for small n n n n,

l_λ and k_λ, where l_λ ≤ l ≤ n and k_λ ≤ k ≤ n , Chebyshev’s inequality gives the inequality

4. SIMULATION

Based on Theorem 3.1 we can approximate the sample paths of {B_h(t,s) : (t, s) ∈ I} with those of

p {∖s,k∣ ≥ ■ }=p.

kl

∑ ∑ε_j

j=1 i=1

λn²

≥₃

the sequence of partial

{ ¹T_n(E_n_×_n)(t,s): (t, s) ∈ I}

n n≥1

sums processes see Figure 1.

kl

9∑ ∑ h(i /ⁿ, j /ⁿ)

j =1 i=1

^≤ 42

nλ

_≤ 9M λ^{2 ,}

where M is the bound of the function h .

Consequently,

N=30, e_ij~N(0,ij/n^2)

N=40, e_ij~N(0,ij/n^2)

variance given by the function h(t, s) = ts , for (t, s) ∈ I.

Begin algorithm

Figure 1. Approximated sample paths of

{Bh(t,s):(t,s)∈ I}

The simulation is developed by using the software package S-PLUS for several sample sizes, i.e., n = 20, 25, 30 and 40 in which the components of En×_n are generated from normal distribution with mean zero and variance given by the function h (t, s) = ts , for (t, s) ∈ I. The figure shows that the sample paths of {B_h(t,s):(t,s)∈ I} are typically unbounded in variation as well as not differentiable on I.

By Corollary 1, we can also approximate the quantiles of the statistics K , KS , and CR defined in Section 1 by using Monte Carlo simulation by the fact that for n → ∞,

Step 1: Fixed nin N

Step 2: Generate M i.i.d. pseudo random matrices

En×n whose components in the kt h row and l th column are generated from

N(o, h (^l ,^k)), 1 ≤ j ≤ M . nn

Step 3: Calculate

Kn^^:=,^max ^-Tn⁽En×n⁾⁽n’n)' 1≤L,k≤n n

Step 4: Calculate the simulated (1 — α) -quantiles of

K: Sort all M values of K_n⁽^j⁾ in ascending order. Let K_n⁽^M^:^j⁾ be the j’th smallest value, (M:1) (M:M )

i.e. Kn ' ≤ L ≤ κn s , the simulated (1 — α) of K is given by

^c1—α ^:= 1

v(M∙M(1—α))

KA ^v " ,if M(1 — α)∈ N;

„ (M : [M(1 — α)])+1 ₁

KA ' , otherwise.

max ¹T (E )(^L,^k) >

(1 ≤L,k≤nn ^{n n}×^{n nn}

<

and

n≥1

max T (E )(^l,^k)

1≤L,k≤nn ^{n n}×^{n nn}

-1 ∑ ∑ (¹ T (E )(^L,^k))² >

^_n²k=0L=0nn ^{n n} n n'n≥

-D→ sup B (t,s), 0≤ t, s≤1 h

sup B (t, s) 0≤ t, s≤1 h

-D→∫b2 (t, s)λj (dt, ds).

The following algorithm is applied to approximate (1 — α) ×100% quantiles of the Kolmogorov type statistic (K), for preassigned values of α ∈ (0,1) . The simulation results developed by using the software package S-PLUS for the statistics K , KS and CR under several choices of sample sizes and αare presented in Table 1. For the simulation we generate the components of E_n_×_nfrom normal distribution with mean zero and

End algorithm

We note that the algorithm is given for the Kolmogorov type statistic only since the algorithm for other statistics can be constructed analogously. The constants c^~ , q^~ , and ^~t presented in

tα tα tα

Table 1 are real numbers that satisfy the conditions

P{K ≥ ~ J = α, P{KS ≥ ~₁^} = α and

tα tα

P{CR ≥ t₁_—_α} = α.

Table1 1. Approximated quantiles of K, KS , and C R

M = 500	(1-α)
M = 500	0.500	0.650	0.750	0.800	0.850	0.900	0.950	0.975	0.990
~ c1-α	0.3726	0.4573	0.5171	0.5594	0.6044	0.6716	0.7326	0.7761	0.8482
n = ²⁰ ~1-α	0.5356	0.5867	0.6318	0.6712	0.7095	0.7552	0.8125	0.8675	0.9373
~ ^t1-α	0.0216	0.0268	0.0335	0.0376	0.0427	0.0526	0.0725	0.0954	0.1246
c1-α	0.3984	0.4801	0.5362	0.5731	0.6139	0.6647	0.7578	0.8433	0.9537
n = 30 ~1-α	0.5384	0.6010	0.6511	0.6659	0.7060	0.7398	0.8121	0.8505	0.9062
~ ^t1-α	0.0212	0.0268	0.0341	0.0383	0.0451	0.0566	0.0702	0.0951	0.1189
~ c1-α	0.4400	0.5193	0.5732	0.5993	0.6504	0.7008	0.7690	0.8048	0.8824
n = 40 ~1-α	0.5429	0.6133	0.6612	0.6857	0.7185	0.7674	0.8325	0.8734	1.0074
~ ^t1-α	0.0211	0.0272	0.0336	0.0399	0.0463	0.0543	0.0723	0.0829	0.1076

5. CONCLUSION

The stochastic process {Bh(t,s):(t,s)∈ I} can be constructed as the limit process of the sequence

1¹T₁ (En×„«t ∙ s^): (t ■ s) ∈ ¹ }

[ n n n × nn≥ι

by applying the Lindeberg’s central limit theorem and the notion of weak convergence of a sequence of probability measures on a metric space. It is also shown by this result that the h -generalized standard Brownian sheet exists. As by products the quantiles of the Kolmogorov, Kolmogorov-Smirnov and Cramér-von Mises type statistics which are very important in change-point as well as in model-check problems can be approximated by simulation.

REFERENCES

MacNeill, B., Mao, Y. and Xie, L. 1994. Modelling Heteroscedastic Age-period-cohort Cancer Data. The Canadian Journal of Statistics. 22 (4): 529—539.

Park, W.J. 1971. Weak convergence of probability measures on the function space C[θ,1]2. J. of Multivariate Analysis. 1: 433—444.

Kuelbs, J. 1968. The Invariance Principle for a Lattice of Random Variables. The Annals of Mathematical Statistics. 39(2): 382—389.

Billingsley, P. 1995. Probability and Measure (third edition). John Wiley & Sons, Inc. New York.

Billingsley, P. 1999. Convergence of Probability Measures (2nd. edition). John Wiley & Sons, Inc. New York.

Jurnal Matematika, Vol. 1, No. 1, 2010, 8—15

PEMODELAN ALJABAR MAX-PLUS DAN EVALUASI KINERJA JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK DENGAN KAPASITAS PENYANGGA TAKHINGGA

¹M. ANDY RUDHITO, ²SRI WAHYUNI, ³ARI SUPARWANTO, DAN ⁴F. SUSILO ¹Mahasiswa S3 Matematika FMIPA UGM dan Staff Pengajar FKIP Universitas Sanata Dharma, Yogyakarta

^2,3 Jurusan Matematika, FMIPA Universitas Gadjah Mada, Yogyakarta ⁴Jurusan Matematika, FST Universitas Sanata Dharma,Yogyakarta

Email : ¹[email protected], ²[email protected], ³[email protected], ⁴[email protected]

INTISARI

Makalah ini membahas tentang pemodelan dan penentuan waktu penyelesaian siklus (cycle) layanan jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga, dengan menggunakan aljabar max-plus. Hasil pembahasan menunjukkan bahwa dinamika jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga dapat dimodelkan ke dalam suatu persamaan matriks atas aljabar max-plus. Dapat ditunjukkan pula bahwa waktu siklus layanan jaringan antrian merupakan eigennilai max-plus dari matriks pada persamaan tersebut.dsfsdlkslkflskfslkflkflsdkfjlskflskjflsdlkjlklkl

Kata kunci: aljabar max-plus, eigennilai max-plus, jaringan antrian fork-join, waktu penyelesaian siklus layanan.

MAX-PLUS ALGEBRA MODELLING AND PERFORMANCE EVALUATION OF QUEUEING NONCYCLIC FORK-JOIN NETWORK WITH INFITE BUFFER CAPACITY

¹M. ANDY RUDHITO, ²SRI WAHYUNI, ³ARI SUPARWANTO, DAN ⁴F. SUSILO

¹PhD Students at Mathematics Department,FMIPA, UGM and Lecturer at FKIP, Sanata Dharma University, Yogyakarta

^2,3 Mathematics Department, FMIPA, Gadjah Mada University, Yogyakarta

⁴Mathematics Department, FST, Sanata Dharma University,Yogyakarta

Email : ¹[email protected], ²[email protected], ³[email protected], ⁴[email protected]

ABSTRACT

This paper aims to model and determine the service cycle completion time of noncyclic fork-join queueing networks with infinite buffer capacity, using max-plus algebra. The finding show that the dynamics of the noncyclic fork-join queuing networks with infinite buffer capacity can be modeled into a matrix equation over max-plus algebra. We can also show that the service cycle completion time of queuing networks is a max-plus eigenvalues of the matrix in the equation.slklsklslsllsllllllllllllllllllllll

Keywords: max-plus algebra, max-plus eigenvalues, fork-join queueing networks, service cycle completion time.

1. PENDAHULUAN

Jaringan fork-join merupakan salah satu sistem antrian yang memungkinkan pelanggan (customer) terpecah menjadi beberapa bagian, dan digabung kembali menjadi satu setelah pelanggan melalui sistem tersebut. Sistem seperti ini banyak dijumpai pada proses produksi dalam industri, pengiriman pesan dalam jaringan komunikasi, dan pemrosesan data dalam sistem komputer multiprosesor. Sebagai gambaran dalam jaringan komunikasi, pesan terpecah menjadi paket-paket yang disampaikan melalui jalur

terpisah, kemudian digabungkan kembali di titik tujuan jaringan tersebut hingga diperoleh pesan seperti semula.

Dalam pembahasan jaringan antrian dapat diasumsikan bahwa kapasitas penyangga (buffer) takhingga atau berhingga. Pemodelan dinamika jaringan dengan menggunakan aljabar max-plus dapat memberikan deskripsi yang lebih kompak dan terpadu (Baccelli et al., 1992). Di samping itu pemodelan ini juga memudahkan dalam hal komputasi numeriknya. Pemodelan jaringan antrian dengan menggunakan aljabar max-plus telah mulai

dibahas dalam Krivulin (1994, 1995, 1996a, 1996b). Dalam Krivulin (1994) telah dibahas pemodelan untuk antrian jenis G/G/1. Pemodelan dan evaluasi kinerja, yang meliputi waktu sistem pelanggan dan waktu tunggu pelanggan, untuk sistem antrian tandem telah dibahas dalam Krivulin (1995). Dalam literatur tersebut pembahasan secara eksplisit baru dibahas untuk sistem antrian tandem dengan kapasitas penyangga takhingga. Dalam Krivulin (1996a) untuk jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga telah diberikan persamaan dinamika keadaan (state dynamic equation) secara eksplisit, dan sistem antrian tandem dipandang sebagai kejadian khususnya. Persamaan keadaan dinamik secara eksplisit untuk jaringan antrian fork-join taksiklik dengan kapasitas penyangga berhingga telah diberikan dalam Krivulin (1996b). Pemodelan yang dilakukan dalam Krivulin (1996a, 1996b), diasumsikan bahwa pada waktu awal jaringan beroperasi, penyangga tidak selalu kosong.

Makalah ini akan membahas pemodelan dan kinerja (performance) jaringan antrian fork-join taksiklik dengan kapasitas penyangga takhingga, dengan kondisi pada awal jaringan beroperasi, penyangga dalam keadaan kosong. Pemodelan dilakukan dengan pendekatan aljabar max-plus. Kinerja jaringan yang dibahas adalah analisis waktu penyelesaian siklus layanan jaringan antrian dikaitkan dengan eigennilaialjabar max-plus.

2. ALJABAR MAX-PLUS DAN TEORI GRAF

Dalam bagian ini dibahas konsep dasar aljabar max-plus dan kaitannya dengan teori graf yang akan digunakan dalam pembahasan untuk bagian-bagian selanjutnya. Materi lebih lengkap dapat dilihat pada Baccelli et al. (1992), Krivulin (1996b), dan Rudhito (2003).

Diberikan Rε : = R ∪{ε } dengan R adalah himpunan semua bilangan real dan ε : = -∞. Pada R _ε didefinisikan operasi berikut: ∀a,b ∈ R_ε , a ⊕ b := max(a, b) dan a ⊗ b : = a + b. (Rε, ⊕, ⊗) merupakan semigelanggang komutatif idempoten dengan elemen netral ε = -∞ dan elemen satuan e = 0, yaitu bahwa ∀a,b ∈ R_ε berlaku:

i) a ⊕ b = b ⊕ a, (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c), a ⊕ ε = a.
ii) (a ⊗ b) ⊗ c = a ⊗ (b ⊗ c) , a ⊗ e = a + 0 = a = 0 + a = e ⊗ a.
iii) a ⊗ ε = ε ⊗ a .
iv) (a ⊕ b) ⊗ c = (a ⊗ c) ⊕ (b ⊗ c), a ⊗ (b ⊕ c) = (a ⊗ b) ⊕ (a ⊗ c).
v) a ⊗ b = b ⊗ a dan a ⊕ a = a.

Lebih lanjut (R_ε, ⊕, ⊗) merupakan semilapangan (semifield), yaitu bahwa (Rε, ⊕, ⊗) merupakan semigelanggang (semigelanggang) komutatif dengan kondisi untuk setiap a ∈ R terdapat -a sehingga berlaku a ⊗ (-a) = 0. Rmax : = (Rε, ⊕, ⊗) disebut dengan aljabar max-plus, yang selanjutnya cukup dituliskan dengan Rmax. Dalam hal urutan pengoperasian (jika tanda kurang tidak dituliskan), operasi ⊗ mempunyai prioritas yang lebih tinggi dari pada operasi ⊕. Pangkat k dari elemen x ∈ R dinotasikan dengan x^⊗ didefinisikan sebagai berikut:

0

x^⊗ : = 0

dan

_⊗k _⊗k-1

x : = x ⊗ x ,

dan didefinisikan pula

0

ε^⊗ : = 0

dan

⊗^k

ε : = ε , untuk k = 1, 2, ....

Operasi ⊕ dan ⊗ pada Rmax di atas dapat

diperluas untuk operasi-operasi matriks dalam

R^m^×ⁿ . Khususnya untuk matriks dalam Rⁿ^×ⁿmax max

didefinisikan

(A ⊕ B)ij = Aij ⊕ Bij dan

n

(A ⊗ B)ij = ⊕Aik⊗Bkj.

k=1

Didefinisikan matriks E ∈ Rⁿ^×ⁿ , max

(E )ij

dan matriks

0 , jika i = j ε , jika i ≠ j

ε ∈ R^mma^×xⁿ , (ε )ij := ε

untuk setiap i dan j . (Rⁿ_m^×_aⁿ_x , ⊕, ⊗) merupakan semigelanggang (semiring) idempoten dengan

elemen netral matriks ε dan elemen satuan matriks E. Pangkat k dari matriks A ∈ Rⁿ_m^x_aⁿ_x dalam aljabar max-plus didefinisikan dengan A^⊗⁰ = En dan A^⊗^k = A ⊗ A^⊗^k^-¹ untuk k = 1, 2, .... Selanjutnya akibat sifat idempoten operasi ⊕, untuk setiap A ∈ R^nxn berlaku (E⊕A)^q = E ⊕ A ⊕ ... ⊕ A^q. max

Suatu graf berarah G didefinisikan sebagai suatu pasangan G = (V, A) dengan V adalah suatu himpunan berhingga takkosong yang anggotanya disebut titik dan A adalah suatu himpunan pasangan terurut titik-titik. Anggota A disebut busur. Suatu lintasan dalam graf berarah G adalah suatu barisan berhingga busur (i1, i2), (i2, i3), ... , (il-1, il) dengan (ik,

i_k+₁) ∈ A untuk suatu l ∈ Ν (= himpunan semua bilangan asli), dan k = 1, 2, ... , l - 1. Untuk suatu lintasan ρ, panjang lintasan ρ didefinisikan sebagai banyak busur yang menyusun ρ dan dinotasikan dengan ρ_l . Suatu lintasan disebut sirkuit jika titik awal dan titik akhirnya sama. Sirkuit elementer adalah sirkuit yang titik-titiknya muncul tidak lebih dari sekali, kecuali titik awal yang muncul tepat dua kali. Suatu graf berarah G = (V, A) dengan V = {1, 2, , ... , n} dikatakan terhubung kuat jika untuk setiap i, j ∈ V , i ≠ j , terdapat suatu lintasan dari i ke j . Suatu graf yang memuat sirkuit disebut graf siklik, sedangkan suatu graf yang tidak memuat sirkuit disebut graf taksiklik.

Untuk setiap graf berarah G = (V, A) dengan n titik, didefinisikan suatu matriks G ∈ Rⁿ_m^×_aⁿ_x , yang disebut dengan matriks kedampingan dari graf berarah G , dengan unsur-unsurnya adalah

0, jika ( j,i) ∈ A;

.

ε, jika (j,i) ∉ A.

Gj = i

Diberikan graf berarah G = (V, A) dengan V = {1, 2, ... , p}. Graf berarah G dikatakan berbobot jika setiap busur (j, i) ∈ A dikawankan dengan suatu bilangan real A_ij. Bilangan real A_ij disebut bobot busur (j, i), dinotasikan dengan w(j, i). Dalam penyajiannya dengan gambar untuk graf berarah berbobot, busur diberi label dengan bobotnya. Didefinisikan graf preseden dari matriks A ∈ Rⁿ_m^×_aⁿ_xadalah graf berarah berbobot G(A) = (V, A) dengan V = {1, 2, ... , n}, A = {(j, i) | w(i, j) = Aij ≠ ε }. Perhatikan sebaliknya bahwa untuk setiap graf berarah berbobot G = (V, A) selalu dapat didefinisikan suatu matriks A ∈ Rⁿ_m^×_aⁿ_x , dengan

W j, i), jika (j, i) ∈ A ε, jika (j, i) ∉ A.

Aj = ‘

Jelas bahwa graf berarah berbobot tersebut merupakan graf preseden dari A.

Diberikan graf berarah berbobot G = (V, A) dengan V = {1, 2, ... , n}. Bobot suatu lintasan ρ = i1 → i₂ → ... → i_l didefinisikan sebagai jumlahan bobot busur-busur yang menyusun ρ . Bobot lintasan ρ dinotasikan dengan ρ_w . Untuk matriks A ∈ Rⁿ^×ⁿ , bobot suatu lintasan lintasan ρ = i → i → max

L → i_l dalam graf preseden G(A) adalah ρ_w =

A +A + L +A . Bobot rata-rata lintasan i 2 ^, i1 i 3 ^, i 2 il^, il-1

ρ, dinotasikan dengan ρ , didefinisikan sebagai

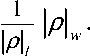
Berikut diberikan suatu interpretasi dalam teori graf untuk pangkat k matriks A ∈ Rⁿ_m^×_aⁿ_x dalam aljabar max-plus. Diberikan A∈ Rⁿ_m^×_aⁿ_x . Jika k ∈ Ν ,

maka unsur ke-st dari matriks A^⊗^k adalah (A^⊗^k )_st

= max (A + L +A +A ) = s ’ ik-1 ¹2 ’ i1 i1 ’ t'

¹≤^k1^,^k2 Lik-1 ≤ n

max ( A +A +

₁ , i1, t i 2, i1

¹≤^k1^,^k2 Lik-1 ≤n

L +A ) untuk

s, ik-1 ⁷

setiap s^, t. Karena ( A₁t + Ai2, i₁+ ^l + ^Asi_k-₁) adalah bobot lintasan dengan panjang k dengan t sebagai titik awal dan s sebagai titik akhirnya dalam G(A), maka (A^⊗^k )_st adalah bobot maksimum semua lintasan dalam G(A) dengan panjang k, dengan t sebagai titik awal dan s sebagai titik akhirnya. Jika tidak ada lintasan dengan panjang k dari t ke s, maka bobot maksimum didefinisikan sama dengan ε.

Sekarang diperhatikan bobot rata-rata maksimum sirkuit elementer, dengan maksimum diambil atas semua sirkuit elementer dalam graf. Diberikan A ∈ Rⁿ_m^×_aⁿ_x dengan graf presedennya G (A) = (V, E ). Bobot maksimum dari semua sirkuit dengan panjang k dengan titik i sebagai titik awal dan titik akhir dalam G(A) dituliskan sebagai (A^⊗^k )_ii . Maksimum dari bobot maksimum semua sirkuit dengan panjang k dengan titik i sebagai titik awal dan titik akhir n_kdalam G(A) atas seluruh titik i adalah ⊕ (A^⊗ )_iii=1

yang dapat dituliskan sebagai trace(A^⊗^k ) dan rata-ratanya adalah (1/k) trace(A^⊗^k) . Kemudian

diambil maksimum atas sirkuit dengan panjang k ≤ n, yaitu atas semua sirkuit elementer, diperoleh suatu rumus untuk bobot rata-rata maksimum sirkuit elementer dalam G(A) (dinotasikan dengan λ_max(A)), n

sebagai berikut: λ_max(A) = ⊕_k₌₁ [(1/k) trace(A^⊗^k ) ]_.

Suatu sirkuit dalam graf G disebut sirkuit kritis jika bobot rata-ratanya sama dengan bobot rata-rata maksimum sirkuit elementer dalam G. Suatu graf yang terdiri dari semua sirkuit kritis dari graf G disebut graf kritis dari G dan dinotasikan dengan G^c.

Berikut diberikan definisi dan teorema yang pembuktiannya dapat dilihat dalam Rudhito (2003).

Teorema 1. (Baccelli, et al., 2001). Diberikan A ∈ Rⁿ_m^×_aⁿ_x. Jika semua sirkuit dalam G(A) mempunyai bobot nonpositif, maka

∀p ≥ n , A^⊗^p pm E ⊕ A ⊕L⊕ A^⊗ⁿ^-¹ .

Bukti : lihat Baccelli et al. (2001) atau Rudhito (2003). ■

Berdasarkan Teorema 1 di atas didefinisikan operasi bintang (∗) untuk matriks berikut ini.

Definisi 1. (Baccelli, et.al., 2001) Diberikan A ∈ Rⁿ_m^×_aⁿ_x dengan semua sirkuit dalam G(A) mempunyai bobot nonpositif . Didefinisikan n n+1

A^* : = E ⊕ A ⊕ L ⊕ A ^⊗ ⊕ A ^⊗ ⊕ L dan

A⁺ : = A ⊗ A^*.

Definisi 2. (Eigennilai dan eigenvektor aljabar maxplus). Diberikan A ∈ Rⁿ_m^×_aⁿ_x . Skalar λ ∈ R_max disebut eigennilai aljabar max-plus matriks A jika terdapat suatu vektor v ∈ Rⁿ_max dengan v ≠ ε_n_×₁ sehingga A ⊗ v = λ ⊗ v. Vektor v tersebut disebut eigenvektor aljabar max-plus matriks A yang bersesuaian dengan λ.

Berikut teorema yang memberikan eksistensi eigennilai aljabar max-plus untuk setiap A ∈ Rⁿ_m^×_aⁿ_x .

Teorema 2. (Baccelli, et al., 2001). Diberikan A ∈Rⁿ_m^×_aⁿ_x . Skalar λmax(A), yaitu bobot rata-rata maksimum sirkuit elementer dalam G(A), merupakan suatu eigennilai aljabar max-plus matriks A.

Bukti:

lihat Baccelli, et al., (2001) atau Rudhito (2003).

■

Dalam Rudhito (2003) dijelaskan bahwa jika titik i menyusun busur dalam sirkuit kritis ρ0 dalam G(A) *

, maka kolom ke-i matriks B merupakan eigenvektor yang bersesuaian dengan eigennilai λmax(A), dengan B = -λmax(A) ⊗ A, dan B^* = E ⊕ B n -1

⊕ L ⊕ B^⊗ .

Berikut diberikan suatu teorema yang memberikan syarat perlu eigennilaialjabar max-plus suatu matriks.

Teorema 3. ( Baccelli, et.al., 2001) Diberikan A ∈Rⁿ_m^×_aⁿ_x . Jika skalar λ ∈ R, merupakan eigennilai aljabar max-plus matriks A, maka λ merupakan bobot rata-rata suatu sirkuit dalam G(A).

Bukti:

lihat Baccelli, et al. (2001) atau Rudhito (2003).

■

Dari Teorema 2 dan 3 dapat disimpulkan bahwa untuk A ∈ Rⁿ_m^×_aⁿ_x , λ_max(A) merupakan eigennilai aljabar max-plus maksimum matriks A. Berikut diberikan lema-lema yang akan melandasi pembahasan selanjutnya.

Lema 4. Jika A ∈ R ⁿ^×ⁿ adalah matriks max

kedampingan graf berarah taksiklik G, maka A^⊗^q = ε , untuk semua q > p, dengan p adalah panjang lintasan terpanjang dari G.

Bukti:

Perhatikan bahwa untuk matriks kedampingan di atas, unsur ke-st dari matriks A^⊗^k adalah

^⊗^k = max (A +A + L +A ), _st i₁ , t i₂ , i₁ s, i_k_-₁

1≤i₁ ,i₂ ,Li_k_-₁≤n

untuk setiap s, t. Perhatikan bahwa (A^⊗^k )_st ≠ ε jika dan hanya jika ada sedikitnya satu lintasan dengan panjang k, dengan s sebagai titik awal dan t sebagai titik akhirnya. Andaikan graf berarah di atas siklik, maka selalu dapat dibuat lintasan pada suatu sirkuitnya dengan panjang berapa pun. Hal ini berakibat bahwa A^⊗^q ≠ ε , untuk semua q = 1, 2, .... Jadi jika graf berarah G di atas taksiklik, maka A^⊗^q = ε , untuk semua q > p, dengan p adalah panjang lintasan terpanjangnya. ■

Lema 5. Diberikan A ∈ Rⁿ^×ⁿ dan b ∈Rⁿ dengan max max

unsur-unsurnya positif atau sama dengan ε . Jika graf, dengan matriks A merupakan matriks kedampingannya, taksiklik, maka persamaan x = A ⊗ x ⊕ b mempunyai penyelesaian tunggal. Lebih lanjut penyelesaian diberikan oleh x = (E ⊕ A)^p ⊗ b, dengan p adalah panjang lintasan terpanjang dalam graf tersebut.

Bukti:

Dengan mensubstitusikan x pada persamaan di atas sebanyak q kali (q > p) diperoleh

Substitusi ke-1 :

x = A ⊗ (A ⊗ x ⊕ b ) ⊕ b

2

= A^⊗ ⊗ x ⊕ A ⊗ b ⊕ b

2

= A^⊗ ⊗ x ⊕ (E ⊕ A) ⊗ b.

Substitusi ke-2 :

x = A^⊗³⊗ x ⊕ (E ⊕ A ⊕A^⊗²) ⊗ b.

Substitusi ke-q :

x = A^⊗^q⁺¹ ⊗ x ⊕ (E ⊕ A ⊕L ⊕A^⊗^q) ⊗ b. Mengingat graf di atas taksiklik maka A^⊗^q = ε , untuk semua q > p, sehingga diperoleh

x = (E ⊕ A ⊕L⊕A^⊗^p ) ⊗ b = (E ⊕ A)^p ⊗ b.

Dari proses mencari penentuan penyelesaian di atas nampak bahwa penyelesaian tersebut tunggal. ■

3. MODEL JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK

Dengan notasi aljabar max-plus persamaan (1) dan

(2) dapat dituliskan sebagai berikut

di(k) = tik ⊗ ai(k) ⊕ tik ⊗ di(k-1)

ai(k) =

ε, ,jika P (i) = φ.

Pengertian tentang jaringan antrian fork-joint berikut mengikuti dalam Krivulin (2000). Diperhatikan suatu jaringan dengan n titik pelayan tunggal (single-server) dan pelanggan kelas tunggal (single-class). Struktur jaringan antrian ini dapat dinyatakan dengan graf berarah taksiklik G = (N, A) dengan busur yang ditentukan oleh rute transisi pelanggan. Untuk setiap titik i ∈ N, didefinisikan himpunan pendahulu (predecessors) dan penerus (successors) titik i berturut-turut dengan P(i) = { j | (j, i) ∈ A ) dan S(i) = { j | (j, i) ∈ A ).

Untuk setiap titik i ∈ N terdiri dari sebuah pelayan dan penyangga dengan kapasitas takhingga yang bekerja dengan prinsip First-In First-Out (FIFO). Pada waktu-awal jaringan bekerja diasumsikan bahwa pelayan bebas pelanggan, penyangga untuk semua titik i dengan P(i) ≠ ∅ dalam keadaan kosong, sedangkan penyangga titik yang tidak mempunyai pendahulu (P(i) = ∅) mempunyai takhingga banyak pelanggan.

Operasi fork pada titik i diawali setiap kali layanan sebuah pelanggan selesai dan diperoleh beberapa pelanggan baru untuk antrian berikutnya. Banyaknya pelanggan baru yang muncul pada titik i sebanyak titik dalam S(i). Pelanggan-pelanggan baru ini secara serentak meninggalkan titik i dan menuju titik-titik j ∈ S(i) secara terpisah. Operasi join pada titik i terjadi saat pelanggan-pelanggan datang ke titik i , tidak hanya di menunggu di penyangga, tetapi juga menunggu sedikitnya satu pelanggan dari setiap titik j ∈ P(i) datang. Segera setelah pelanggan datang, bersama satu pelanggan dari setiap titik pendahulunya, mereka bersatu menjadi satu pelanggan dan masuk dalam penyangga dalam pelayan berikutnya. Dalam pengoperasian jaringan ini diasumsikan bahwa perpindahan pelanggan antar titik tidak memerlukan waktu.

Misalkan d(k) = [ d1(k) , d2(k), ... , dn(k)]^T , a1(k) , a2(k), ... , an(k)]^T dan

(3)

(4)

a(k) = [

Tk =

t1k

ε

t

nk _

Persamaan (3) dan (4) di atas

menjadi

dapat dituliskan

d(k) = Tk ⊗ a(k) ⊕ Tk ⊗ d(k -1).

a(k) = G ⊗ d(k),

dengan matriks G yang unsur-unsur adalah

Gij = ^,

0, jika j∈ P(i) ; ε, untuk yang lain.

(5)

(6)

Perhatikan bahwa G merupakan matriks

kedampingan dari graf stuktur jaringan antrian. Dari persamaan (5) dan (6) dapat dituliskan persamaan

d(k) = Tk ⊗ G ⊗ d(k) ⊕ Tk ⊗ d(k -1). (7)

Teorema 6. Diberikan jaringan antrian fork-join tak siklik dengan graf struktur jaringannya yang mempunyai panjang lintasan terpanjang p dan matriks kedampingan G. Persamaan keadaan eksplisit jaringan tersebut adalah

d(k) = A(k) ⊗ d(k -1), (8) dengan A(k) = (E ⊕ (Tk ⊗ G))^p ⊗ Tk .

Misalkan a_i(k) menyatakan waktu kedatangan pelanggan ke-k pada titik i, di(k) menyatakan waktu keberangkatan pelanggan ke-k pada titik i, dan tik menyatakan lama waktu layanan untuk pelanggan ke-k pada pelayan i. Diasumsikan jaringan mulai beroperasi pada nol waktu, yaitu bahwa di(0) = 0 dan

Bukti:

Dari hasil pada persamaan (7) dapat dituliskan d(k) = (Tk ⊗ G) ⊗ d(k) ⊕ (Tk ⊗ d(k -1)). Karena G adalah matriks kedampingan graf taksiklik dengan panjang lintasan p, maka menurut Lema 4, G^⊗^q = ε untuk semua q > p. Akibatnya (T_k ⊗ G))^q = ε untuk semua q > p. Selanjutnya menurut Lema 5, persamaan ini mempunyai penyelesaian

d(k) = (E ⊕ (Tk ⊗ G))^p ⊗ (Tk ⊗ d(k -1))

= ((E ⊕ (Tk ⊗ G))^p ⊗ Tk ) ⊗ d(k -1)).

■

Contoh 1.

Jaringan antrian fork-join taksiklik dengan n = 5 diperlihatkan dalam Gambar 1 berikut.

di(k) = ε untuk semua k < 0, i = 1, ..., n. Dinamika

antrian pada titik i dapat dinyatakan dengan

di(k) = max(tik + ai(k), tik + di(k- 1)) ,

ai(k) =

max (d _j (k)), jika P(i) ≠ φ, < j ∈ P (i) j

ε, jika P (i) = φ.

(1)

(2)

Gambar 1.

' d 1(2)'		' 2	ε	ε	ε	ε'		' 2'		' 4'
d 2(2)		ε	3	ε	ε	ε		3		6
d 3(2)	=	7	ε	5	ε	ε	®	7	=	12
d 4(2)		⁶	7	ε	4	ε		⁷		¹¹
. d 5(2).		.¹⁰	10	8	7	3_.		.10.		15

Dengan menggunakan program Matlab, diperoleh perhitungan hingga k = 30, seperti dalam Tabel 1 berikut.

Matriks kedampingan dari graf pada jaringan di atas adalah

	ε	ε	ε	ε	ε
	ε	ε	ε	ε	ε
G =	0	ε	ε	ε	ε
	⁰	0	ε	ε	^ε
	.^ε	ε	0	0	^ε.

Nampak bahwa panjang lintasan terpanjangnya adalah p = 2. Dari persamaan (8) diperoleh persamaan keadaan

d(k) = A(k) ⊗ d(k -1) , dengan

A(k) = (E ⊕ (Tk ⊗ G))² ⊗ Tk

= (E ⊕ (Tk ⊗ G) ⊕ (Tk ⊗ G)²) ⊗ Tk

t1k	ε	ε	ε	ε
ε	t2k	ε	ε	^ε
t1k ^⊗t3k	ε	t3k	ε	ε
t1k ^⊗t4k	t2k ^⊗t4k	ε	t4k	^ε
t1k⊗(t3k⊕t4k)⊗t5k	t₂_k ⊗t₄_k ⊗t₅_k	t₃_k ⊗t₅_k	t₄_k ⊗t₅_k	t5k.

Misalkan lama waktu layanan untuk pelanggan ke-k pada pelayan i adalah sebagai berikut: t₁_k = 2, t₂_k = 3, t3k = 5, t4k = 4 dan t5k = 3, maka diperoleh

	’ 2	ε	ε	ε	ε
	ε	3	ε	ε	ε
A(k) =	7	ε	5	ε	ε
	⁶	7	ε	4	ε
	.10	10	8	7	3

Sehingga untuk k = 1, 2 diperoleh

’ d 1(1)'		’ 2	ε	ε	ε	ε ’		'0'		' 2'
d 2(1)		ε	3	ε	ε	ε		0		3
d 3(1)	=	7	ε	5	ε	ε	®	⁰	=	⁷
d 4(1)		⁶	7	ε	4	ε		⁰		⁷
. d 5(1).		.10	10	8	7	3.		.0.		.10.

4. EVALUASI KINERJA JARINGAN ANTRIAN

Diperhatikan waktu penuntasan siklus layanan jaringan sebagai barisan siklus layanan: siklus kepertama mulai saat waktu awal, dan berakhir segera setelah semua pelayan dalam jaringan menuntaskan layanan kepertamanya, siklus kedua berakhir segera setelah semua pelayan dalam jaringan menuntaskan layanan keduanya, dan seterusnya. Dengan demikan waktu penuntasan siklus ke-k pada titik i adalah d_i (k) , sehingga waktu penuntasan siklus ke-k pada jaringan dapat dinyatakan sebagai

maxd_i (k)

i

dengan d_i(0) = 0, i = 1, ..., n dan k = 0, 1, 2, ....

Selanjutnya waktu siklus layanan jaringan dapat dinyatakan dengan:

γ = lim max(d_i (k)) .

k→∞ k i

Contoh 2:

Dari hasil dalam Contoh 1 pada Tabel 1 nampak bahwa waktu penuntasan siklus ke-k dari jaringan tersebut adalah d₅(k). Perhitungan secara numerik mengenai γ dari Contoh 1, diperoleh hasil seperti dalam Tabel 2 berikut.

Nampak dalam contoh ini bahwa nilai

γ = lim max(d_i (k)) k→∞ k i

= lim ¹(d₅(k)) = 5. k→∞ k

Dengan menggunakan program Matlab dapat ditentukan bahwa eigennilai aljabar max-plus maksimum matriks A adalah λmax(A) = 5 dan eigenvektor yang bersesuaian adalah [ε ε 0 ε 3]^T .

Secara umum sifat yang muncul pada contoh-contoh di atas diberikan dalam teorema berikut ini.

Teorema 7. Jaringan antrian fork-join taksiklik kapasitas penyangga takhingga, dengan persamaan keadaan eksplisit jaringan tersebut adalah d(k) =

A(k) ⊗ d(k -1), k = 1, 2, ..., mempunyai waktu penuntasan siklus layanan

γ = lim 1 max(d_i (k)) = λmax(A(k)), k→∞ k i

yaitu eigennilai max-plus maksimum matriks A(k) tersebut.

Bukti:

Perhatikan bahwa

d(k) = A(k) ⊗ d(k -1)

= (A(k) ⊗ A(k-1)⊗ … ⊗A(2) ⊗ A(1)) ⊗ d(0).

Karena dalam tulisan ini diasumsikan bahwa

A(1) = A(2) = ... = A(k)

dan d(0) = 0, maka d(k) = A^⊗^k ⊗ 0 , sehingga di(k) = ma_jx [(A^⊗^k)_ij]

dan

maxd_i (k) = max { max [( A^⊗^k_ij )]}. i ij

Bobot rata-rata maksimum sirkuit elementer dalam graf presede_nn matriks A tersebut λmax(A) = ⊕((1/k) trace(A^⊗^k) ) , k=1

Selanjutnya diperoleh bahwa

di(k) =max [(A^⊗^k) ] = max (λ (A))^⊗^k_j ij _j

sehingga

maxd_i (k) = max (max ( (λ_max (A))^⊗^k ) i ij

=(λmax(A))^⊗^k .

Dengan demikian diperoleh bahwa

γ = lim max(d_i(k)) k→∞ k i

= lim ¹ (λmax (A))^⊗^kk→∞ k

= lim¹ (kλmax(A)) = λmax(A). k→∞ k

■

yang merupakan eigennilai aljabar max-plus maksimum matriks A. Oleh karena itu berlaku

A^⊗^k⊗ v^*= (λmax(A))^⊗^k⊗ v^* ,

untuk suatu eigenvektor v^*. Hal ini berakibat ma_jx((A^⊗^k)_ij⊗ vj^*) = (λ_max(A))^⊗^k ⊗ma_jx(v^*_j) , dengan max (v^* ) ≠ ε . Vektor - max (v^* ) ⊗ v^* juga j^j j^j

merupakan eigenvektor yang berkaitan dengan eigenvektor λmax(A) di atas, dengan

- max (v^* ) ⊗ max (v^* ) = 0.

j^j j^j

Tabel 1. Hasil Perhitungan d(k)

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d1	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
d2	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
d3	7	12	17	22	27	32	37	42	47	52	57	62	67	72	77
d4	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
k	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
d1	32	34	36	38	40	42	44	46	48	50	52	54	56	58	60
d2	48	51	54	57	60	63	66	69	72	75	78	81	84	87	90
d3	82	87	92	97	102	107	112	117	122	127	132	142	147	152	157
d4	67	71	75	79	83	87	91	95	99	103	107	111	115	119	123
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155

Tabel 2. Hasil Perhitungan γ

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
d₅/k	10	7,5	6,67	6,25	6,00	5,83	5,71	5,63	5,56	5,50	5,45	5,42	5,38	5,36	5,33
k	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59
d₅	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155
d₅/k	5,11	5,11	5,11	5,10	5,10	5,10	5,10	5,10	5,09	5,09	5,09	5,09	5,09	5,09	5,08

DAFTAR PUSTAKA

Bacelli, F., et al. 1992. Synchronization and Linearity. New York: John Wiley & Sons.

Krivulin, N.K., 1994. Using Max-Algebra Linear Models in the Representation of Queueing Systems. Proc. 5^th SIAM Conf. on Applied Linear Algebra, Snowbird, AT. June 15-18, 1994. 155—160.

Krivulin, N.K., 1995. A Max-Algebra Approach to Modeling and Simulation of Tandem Queueing Systems. Mathematical and Computer Modelling. 22(3):25—31.

Krivulin, N.K., 1996a. The Max-Plus Algebra Approach in Modelling of Queueing Networks Proc. 1996 SCS Summer Computer Simulation Conference (SCSC-96). July 2125. The Society for Computer Simulation, 485—490.

Krivulin, N.K., 1996b. Max-Plus Algebra Models of Queueing Networks. Proc. Intern. Workshop WODES’96 Univ. of Edinburgh, UK. Aug. 19-21, 1996. IEEE: London. 76—81.

Krivulin, N.K., 2000. Algebraic Modelling and Performance Evaluation, of Acyclic ForkJoin Queueing Networks. Advances in Stochastic Simulation Methods. Birkhauser. Boston. 63—81 .

Rudhito, Andy. 2003. Sistem Linear Max-Plus Waktu-Invariant. Tesis Magister Matematika Program Pascasarjana Universitas Gadjah Mada. Yogyakarta.

BEBERAPA SIFAT IDEAL GELANGGANG POLINOM MIRING: SUATU KAJIAN PUSTAKA

AMIR KAMAL AMIR

Jurusan Matematika, FMIPA, Universitas Hasanuddin 90245 Email : [email protected]

INTISARI

Misalkan R adalah suatu gelanggang dengan elemen satuan 1, σ adalah suatu endomorfisme, dan δ adalah suatu σ — derivatif. Gelanggang polinom miring (skew polynomial) atas R dengan variabel x adalah gelanggang: R[x;σ,δ] = {f (x) = a_nxⁿ + —+ a0 | ai ∈ R} dengan aturan perkalian xa = σ(a)x + δ(a) . Penelitian ini akan mengidentifikasi ideal-ideal dari gelanggang polinom miring dalam hal δ = 0. Lebih jelasnya, akan didentifikasi hal-hal berikut: (1) ideal dari gelanggang polinom miring D[x; σ]; (2) ideal prim dari gelanggang polinom miring K[x; σ]; dan ideal σ — prim dari gelanggang polinom miring D[x; σ].

Kata kunci: automorfisme, daerah integral, σ — prim.

SOME IDEAL PROPERTIES OF

SKEW POLYNOMIAL RING: A LITERATURE STUDY

AMIR KAMAL AMIR

Mathematics Department, FMIPA, Hasanuddin University 90245 Email : [email protected]

ABSTRACT

Let R be a ring with identity 1 and σ be an endomorphism of R and δ be a left σ — derivation. The skew polynomial ring over R in an indeterminate x is: R[x; σ, δ] = {f (x) = a_nxⁿ +-----+ a0 | ai ∈ R} with xa = σ(a)x + δ(a) The aim of this research is to investigate the ideals in the above skew polynomial ring in case of δ = 0 . Precisely, we will investigate the following: (1) the ideal of skew polynomial ring D[x;σ]; (2) the ideal prim of skew polynomial ring K[x;σ]; and (3) the σ — prim ideal of skew polynomial ring D[x; σ].

Keywords: automorphism, integral area, σ — prim.

1. PENDAHULUAN

Definisi dari gelanggang polinom miring (gelanggang takkomutatif) ini pertama kali diperkenalkan oleh Ore (1993) yang mengombinasikan ide awal dari Hilbert (kasus δ=0) dan Schlessinger (kasus σ = 1). Sejak kemunculan artikel dari Ore ini, gelanggang polinom miring telah memerankan peran yang penting dalam teori gelanggang takkomutatif dan telah banyak peneliti yang bergelut dalam teori gelanggang takkomutatif menginvestigasi bentuk gelanggang tersebut dari berbagai sudut pandang, seperti teori ideal, teori order, teori Galois, dan aljabar homologi.

Berikut diberikan definisi lengkap dari gelanggang polinom miring.

Definisi 1. Misalkan R adalah suatu gelanggang dengan identitas 1, σ adalah suatu endomorfisme dari R, dan δ adalah suatu σ — derivatif, yaitu:

(i) . δ adalah suatu endomorfisme pada R, dengan R sebagai grup penjumlahan
(ii) . δ(ab) = σ(a) δ(b) + δ(a)b untuk setiap

a, b ∈ R.

Gelanggang polinom miring atas R dengan variabel x adalah gelanggang:

R[x;σ, δ] = {f (x)=a_nxⁿ + -L + a0 | ai ∈ R } dengan xa = σ( a ) x + δ( a ), V a ∈ R .

Suatu elemen p dari gelanggang polinom miring R[x; σ, δ] mempunyai bentuk kanonik

r

p = ∑ aixⁱ, r∈Z₊={0,1,l}, ai ∈ R, i= 1,l,r. i=0

Apabila σ=1 atau σ adalah suatu endomorfisme identitas, maka gelanggang polinom miring cukup ditulis R[x; δ]. Untuk hal δ=O, gelanggang polinom miring cukup ditulis R[x; σ]. Sedangkan untuk kasus σ = 1 dan δ=O gelanggang polinom miring cukup ditulis R[x] , yang merupakan gelanggang polinom biasa. Dalam tulisan ini gelanggang R yang digunakan adalah gelanggang yang merupakan daerah integral komutatif dengan elemen satuan yang selanjutnya disimbolkan dengan D.

Contoh 1. Misalkan C adalah himpunan bilangan kompleks. σ suatu endomorfisme pada C yang didefinisikan sebagai σ( a + bi ) = a—bi, untuk setiap a + bi∈C , dan δ=O. Akan ditunjukkan ketidak komutatifan dalam gelanggang polinom miring C [ x ;σ].

[ (2 + 3i) x ][ (4+5i) x ]= (2 + 3i) [ x (4+5i)] x

=(2+3i)[σ(4+5i) x ] x

=(2 + 3i)(4—5i) x² = (23 + 2i) x²

[ (4+5i) x ] [ (2+3i) x ]=(4+5i) [ x (2+3i)] x

=(4+5i) [ σ(2+3i) x ] x

=(4+5i)(2—3i) x² = (23—2i) x ²

2. MASALAH DAN PEMBAHASAN

Masalah yang akan dibahas dalam bagian ini adalah mengidentifikasi bentuk-bentuk ideal dari berbagai bentuk gelanggang polinom miring. Secara mendetail, bentuk-bentuk ideal yang akan diidentifikasi adalah sebagai berikut:

1.i deal dari gelanggang polinom miring D[ x; σ];
2.i deal prim dari gelanggang polinom miring K [ x; σ];
3.i deal σ — prim dari gelanggang polinom miring D[ x; σ ].

Sekadar mengingat kembali, berikut ini disajikan definisi dari ideal dan ideal prim.

Definisi 2. Misalkan R adalah suatu gelanggang. Suatu himpunan bagian I dari R dikatakan suatu ideal kanan dari R jika :

1. (I,+) adalah suatu grup bagian dari (R,+),
2. xr berada dalam I untuk setiap x dalam I dan setiap r dalam R.

Suatu ideal kiri dari R didefinisikan serupa dengan ideal kanan. I dikatakan ideal dari R jika I merupakan ideal kanan dan sekaligus ideal kiri dari R. Selanjutnya suatu ideal P dari R dikatakan ideal prim jika dan hanya jika untuk setiap ideal-ideal A, B dari R implikasi berikut bernilai benar: Jika AB ⊂ P , maka A ⊂ P atau B ⊂ P . Pernyataan terakhir ini ekuivalen dengan: jika ab ∈ P, maka a ∈ P atau b ∈ P.

2.1 Ideal dari Gelanggang Polinom Miring R [ x; σ, δ]

Teorema 1. Misalkan D adalah suatu daerah integral komutatif yang bukan merupakan lapangan. Jika σⁿ ≠ 1, untuk semua bilangan asli n dan f (x)D[x;σ] adalah suatu ideal dari D[x;σ], maka f(x) = x.

Bukti:

Misalkan f (x) = fj + flx + l + f_nxⁿ, dengan fi ≠ O untuk suatu i ∈ {1,2, l,n}.

(i) . Akan tunjukkan bahwa f j = O .

Karena f (x) ∈ f (x)D[x;σ], diperoleh

af (x) ∈ f (x) D [ x ;σ], V a ∈ D. Oleh karena itu terdapat b ∈ D sedemikian sehingga af ( x ) = f ( x ) b atau

^a (^fj⁺^f1^x⁺^l⁺^fn^xn) = (^fj⁺^f1^x⁺^l⁺^fn^xn) b.

Dari persamaan ini diperoleh afj = fj b dan afi = fi σ (b). Karena fi ≠ O diperoleh

a = σⁱ (b), yang mengakibatkan a ≠ b sehingga fj = o.

(ii) . Sebagai kosekwensi dari (i), diperoleh f (x)=flx + L + fnxⁿ, (i .e. f j = O) .

Selanjutnya akan tunjukkan bahwa fi ≠ O.

Andaikan bahwa fi = O, maka

f (x)=f2x² + l + fnxⁿ ∈ f (x)d[x;σ].

Dari sini diperoleh,

^f x)=^fx ⁺ L ⁺fnxn =x ^σ^1f)X⁺L ⁺^σ fx

∈^fx)D[^χ^σ

dengan x ∉ f (x)D[xσ] dan

σ^¹(f2)x + ∙∙∙ +σ"¹(f_n)xⁿ^-¹ ∉ f(x)D[x;σ].

Hal ini kontradiksi dengan asumsi bahwa f (x)D[x; σ] adalah ideal prim.

(iii) . Akan tunjukkan bahwa fi = 0, ∀i >1.

Andaikan terdapat suatu k >1 sedemikian sehingga f k ≠ 0. Misalkan t > 1 adalah bilangan terkecil sedemikian sehingga ft ≠ 0.

Dari persamaan

a (^f1^x⁺ L ⁺^fn^xn) = (^f1^x⁺ L ⁺^fn^xn )^b^,pada bagian (i) diperoleh af = fσ( b) dan

af_t = f_t σ (b) . Karena f ≠ 0 dan f_t ≠ 0 , maka

a = σ^t¹ (a). Hal ini kontradiksi dengan σⁿ ≠ 1 untuk semua bilangan asli n.

(iv) . Sekarang dipunyai f (x) = fx . Akan

ditunjukkan bahwa f1 = 1.

Andaikan f1 ≠ 1. Karena D adalah bukan sautu lapangan, maka dapat dipilih suatu b ∈ D sedemikian sehingga

bx ∉ f1 xD[x; σ]=f (x)D[x; σ].

Jelas bahwa

f1 ∉ f (x)D[x;σ]

dan

bx ∉ f (x)D[x; σ]

tetapi f1.bx = fx.σ^-1(b) ∈ f (x)D[xσ].

Hal ini kontradiksi dengan asumsi bahwa f (x)D[ x; σ] adalah suatu ideal prim. Bagian (i) sampai (iv) melengkapi bukti teorema. ■

Lema 1. Misalkan Λ=D[xσ] adalah suatu gelanggang polinom miring dan A adalah ideal dari Λ. A ∩ D = {0} j'ika dan hanya j'ika AK[x;^]0 K[xσ], dalam hal ini K adalah

lapangan pembagian dari D.

Bukti:

(i) . Pada bagian ini akan ditunjukkan bahwa: jika A ∩ D = {0} , maka AK[x; σ] 0 K[x; σ].

Sudah jelas bahwa AK[xσ] ⊆ K[x;d], jadi tinggal ditunjukkan bahwa AK[xσ] ≠ K[x;d], yaitu terdapat g(x) ∈ K[xσ] sedemikian sehingga g(x) ∉ AK[x; σ]. Pilih g(x) = d ∈ D, d ≠ 0 .

Karena A ∩ D = {0} , maka d ∉ AK[x; σ]

sehingga g(x) ∉ AK[x; σ].

(ii) . Pada bagian ini akan ditunjukkan bahwa: jika AK[x; σ] 0 K[x; σ], maka A ∩ D = {0} .

Andaikan A ∩ D ≠ {0} berarti terdapat d ∈ D, d ≠ 0. Ini berarti 1 = dd^¹ ∈ AK[x;σ] yang mengakibatkan AK[x; σ] = K[x; σ] karena AK[x; σ] adalah suatu ideal dalam K[x; σ]. Hal ini kontradiksi dengan AK[x;σ] 0 K[x;ff].«

Teorema 2. Misalkan P adalah ideal prim minimal dari Λ=D[x; σ] dan K adalah lapangan hasil bagi dari D, maka PK[xσ] adalah ideal prim dari K [ x; σ].

Bukti:

(i) . Akan ditunjukkan bahwa PK [ x σ] ideal.

Misalkan g(x) ∈ PK[x; σ] dan h(x) ∈ K[x; σ]. Untuk membuktikan bahwa PK[x; σ] adalah ideal , maka akan ditunjukkan bahwa h (x) g (x) ∈ PK [ x; σ] dan g (x) h (x) ∈ PK [ x; σ]. Karena g(x) ∈ PK[x; σ] berarti

n

g (x) = ∑ ai (x)bi (x) dengan ai (x) ∈ P dan

i=1

bi (x) ∈ K[x;^]. Karena h (x) ∈ K[x;^] dan K adalah lapangan hasil bagi dari D, maka dapat ditemukan d ∈ D, d ≠ 0 sedemikian sehingga dh(x) ∈ D[xσ]. Selanjutnya, dengan alasan yang sama dapat ditemukan juga e ∈ D, e ≠ 0 sedemikian sehingga

dh (x) ai (x) e^-1 bi (x) = h (x) ai (x) bi (x), sehingga diperoleh

nn

h(x) g (x) = h(x )∑ ai (x)b_i (x) = ∑ dh (x) ai (x) e^-1 b_i (x)

i=1 i=1

Karena dh(x) ∈ D[x; σ], ai (x) ∈ P, P adalah ideal

dari D[x; σ], dan e ¹ bi (x) ∈ K[x; σ], maka dapat disimpulkan bahwa:

n

h (x)g (x) = ∑ dh (x)ai (x) e^-1 bi (x) ∈ PK[x; σ |.

i=1

Pada sisi lain,

g(x)h(x) =

n

∑^a⁽)^b⁽..^hx)=∑a⁽..) ⁽h^x)∈ PK

, karena ai (x) ∈ P dan bi (x)h (x) ∈ K[xσ].

(ii) . Akan ditunjukkan bahwa PK[x; σ] prim

Untuk menunjukkan hal ini, akan ditunjukkan bahwa jika g(x)h(x) ∈ PK[x;σ] , maka

g(x)∈ PK[x;σ] atau h(x)∈ PK[x;σ] .

Karena g(x)h(x) ∈ PK[x;σ] , maka dapat

n

dimisalkan g(x)h(x) = ∑ Pi (x)ki (x) , dengan

i=1

p_i(x) ∈ P dan k_i (x) ∈ K[x; σ] untuk suatu n bilangan asli. Karena K adalah lapangan hasil bagi dari D, maka untuk setiap i terdapat d_i ∈ D sedemikian sehingga d_ik_i(x) ∈ D[x;σ] . Oleh karena itu, p_i (x)d_ik_i (x) ∈ P karena P adalah ideal prim dari D[x; σ] . Dari sini sudah dapat disimpulkan bahwa terdapat 0 ≠ d ∈ D sedemikian sehingga

d

n

∑ Pt⁽^x) ^ki⁽^x)

i=1

∈P.

Sehingga

dg(x)h(x) = d

n

∑ Pi⁽^x ) ki⁽^x)

i=1

∈ P.

Selanjutnya, andaikan g(x) ∉ PK[x;σ] dan

h(x) ∉ PK[x;σ] , maka g(x)∉ P dan h(x) ∉ P . Dengan demikian g(x)h(x) ∉ P , karena P ideal prim. Mengingat P ideal prim, dg(x)h(x) ∈ P , dan g(x)h(x) ∉ P , maka d ∈ P yang berarti bahwa P ∩ D = {0} . Hal ini kontradiksi dengan Lema 1. ■

2.2 Ideal σ- prim dari Gelanggang Polinom Miring R[x; σ , δ]

Definisi 3. Misalkan R[x;σ,δ] adalah suatu gelangang polinom miring. Suatu σ- ideal dari R adalah suatu ideal I dari R sedemikian sehingga σ(I) ⊆ I . Suatu σ- ideal prim (atau σ- prim ) adalah suatu σ- ideal murni I dari R sedemikian sehingga jika J, K adalah σ- ideal yang memenuhi JK ⊆ I , maka J ⊆ I atau K ⊆ I . Dalam kasus 0 adalah suatu σ- prim ideal dari R, dikatakan R adalah suatu gelanggang σ- prim .

Teorema 3. Misalkan σ adalah suatu automorfisme dari gelanggang R, dan misalkan I adalah suatu ideal murni dari R sedemikian sehingga σ(I) = I. I

adalah σ- prime jika dan hanya jika untuk sembarang a,c ∈ R - I, terdapat b ∈ R dan t ∈ Z sedemikain sehingga abσⁿ (c) ∉ I .

Bukti:

⇐

Misalkan A, C adalah σ- ideal yang tidak berada dalam ideal I. Pilih elemen-elemen a ∈ A - I dan c ∈ C - I , maka terdapat b ∈ R dan t ∈ Z sedemikian sehingga abσ^t (c) ∉ I .

Kasus 1. Jika t ≥ 0, maka σ^t (c) ∈ C sehingga dari abσ^t (c) ∉ I diperoleh AC ⊄ I .

Kasus 2. Jika t < 0, maka dari abσ^t (c) ∉ I diperoleh σ^-^t (a)σ^-^t (b)c ∉ σ^-^t(I) = I. Dalam kasus ini, σ^-^t (a) ∈ A sehingga AC ⊄ I .

Dari kasus 1 dan 2 disimpulkan bahwa I adalah suatu ideal σ- prime .

⇒

Misalkan I adalah σ- prime dan a,c ∈ R - I. Himpunan-himpunan

∞

A = ∑ R_σⁱ (a) r

i=0

dan

∞

C = ∑ Rσj (c)R

j=0

adalah σ- ideal yang tidak berada dalam ideal I, sehingga AC ⊄ I .

Konsekuensinya, σⁱ (a)bσ^j (c) ∉ I untuk suatu i, j ≥ 0, sehingga aσ^-ⁱ (b)σ^t^-ⁱ (c) ∉ I.

Teorema 4. Misalkan M adalah suatu idel maksimal dari D[x; σ] dengan M ∩ D ≠ {0} .

Jika x ∉ M , maka M ∩ D adalah suatu ideal σ- prime.

Bukti:

(i) . Jelas bahwa M ∩ D adalah suatu ideal
(ii) . Akan ditunjukkan bahwa M ∩ D adalah σ- ideal dengan jalan menunjukkan bahwa σ(M ∩D) ⊆ M ∩D . Ambil a∈ M ∩D dan andaikan σ(a) ∉ M ∩ D , maka σ(a) ∉ M , karena σ(a) ∈ D . Dengan demikian σ(a) x ∉ M yang berarti xa ∉ M . Kontradiksi dengan M adalah suatu ideal.
(iii) . Akan ditunjukkan bahwa M ∩ D adalah σ- prime.

Misalkan J dan,K adalah σ- ideal dari D dan JK ⊆ M ∩ D , maka akan ditunjukkan bahwa J ⊆ M ∩ D atau K ⊆ M ∩ D atau sama dengan menunjukkan bahwa jika J ⊄ M ∩ D , maka K ⊆ M ∩ D . Ambil k ∈ K dan pilih j ∈ J tetapi j ∉ M ∩ D . Ini berarti j ∉ M . jk ∈ JK ⊆ M ∩ D , maka jk ∈ M . Karena j ∉ M dan M adalah ideal prim (ideal maksimal pasti merupakan ideal prim), maka k ∈ M . Sehingga diperoleh k ∈ M ∩ D . Hal ini membuktikan bahwa K ⊆ M ∩ D . ■

3. SIMPULAN

Dari paparan di atas dapat ditarik simpulan bahwa:

1. dalam kondisi σⁿ ≠ 1, ideal dari D[x;σ] berbentuk xD[x;σ] ;
2. salah satu bentuk ideal prim dari gelanggang polinom miring K[x; σ] adalah PK[x;σ] , dengan P adalah ideal prim minimal;
3. salah satu bentuk ideal σ- prime dari gelanggang polinom miring D[x; σ] adalah berbentuk M ∩ D dengan M adalah maksimal ideal dari D[x; σ] yang tidak memuat x.

UCAPAN TERIMA KASIH

Terima kasih kepada Prof. Hidetoshi Marubayashi, Tokushima Bunry University, Japan atas masuk-masukan yang telah diberikan.

DAFTAR PUSTAKA

Ore, O. 1933.Theory of Non-Commutative Polynomials. Annals of Mathematics. 34: 480—508.

UJI KENORMALAN UNIVARIAT: SUATU KAJIAN PUSTAKA

I WAYAN SUMARJAYA

Jurusan Matematika, FMIPA, Universitas Udayana Email: [email protected]

INTISARI

Sebagian besar prosedur statistika terutama inferensi statistika mengasumsikan distribusi sampel adalah normal. Asumsi kenormalan ini harus diuji untuk menjamin penggunaan statistik uji yang benar dan sesuai, sehingga nantinya diperoleh simpulan yang sahih. Penelitian ini membahas perkembangan uji-uji kenormalan univariat: uji berdasarkan fungsi distribusi empiris, uji berdasarkan momen, uji berdasarkan korelasi atau regresi, uji berdasarkan entropi sampel, uji berdasarkan metode kernel, uji berdasarkan karakteristik Polya, dan uji berdasarkan metode nonparametrik. Penelitian ini juga membahas uji kenormalan yang mampu mendeteksi pencilan dan uji omnibus yang mampu memberikan informasi tambahan tentang ketidaknormalan. sdfsdllflsdflskdflsklfkslfksdllskflskflsllsdfs

Kata kunci: uji kenormalan univariat, uji kenormalan omnibus.

UNIVARIATE NORMALITY TEST: A LITERATURE STUDY

I WAYAN SUMARJAYA

Mathematics Department, FMIPA, Udayana University Email: [email protected]

ABSTRACT

Almost all statistical procedures, especially statistical inference, assumed that the sample distribution is normally distributed. This normality assumption must be tested to ensure the correct use of the test statistic, hence resulting a correct conclusion. This research discusses some univariate normality tests: test based on empirical distribution function, test based on moments, test based on correlation or regression, test based on sample entropy, test based on kernel method, test based on Polya characteristics, and test based on nonparametric method. This research also discuss normality test that capable of detecting outliers and discuss omnibus test that can give additional information about nonnormality.

Keywords: univariate normality test, omnibus normality test.

1. PENDAHULUAN

Sebagian besar prosedur statistika terutama inferensi statistika mengasumsikan distribusi sampel adalah normal. Asumsi kenormalan ini perlu diuji untuk menjamin penggunaan statistik uji yang benar dan sesuai, sehingga nantinya diperoleh simpulan yang sahih, misalnya pada bidang kesehatan (lihat Lumley, 2002)

Secara umum, uji kenormalan dapat dikelompokkan ke dalam beberapa kategori: uji berdasarkan fungsi distribusi empiris, uji berdasarkan momen, uji berdasarkan korelasi atau regresi, uji berdasarkan entropi, uji berdasarkan karakteristik Polya, uji berdasarkan metode kernel, dan uji berdasarkan metode nonparametrik.

Studi komprehensif perbandingan uji-uji kenormalan telah dilakukan antara lain oleh Stephens (1972), Koziol (1986), Dufour et al.(1998), Seier (2002), Coin dan Corradetti (2006), Farrell dan Rogers-Stewart (2006), Yazici dan Yolacan (2007), Tanweer-ul-Islam (2008), Breton et al. (2008), dan Tanweer-ul-Islam dan Zaman (2008).

Penelitian ini juga membahas uji kenormalan yang mampu mendeteksi pencilan dan uji omnibus yang mampu memberikan informasi tambahan tentang ketidaknormalan distribusi alternatif.

2. METODE-METODE UJI KENORMALAN

UNIVARIAT

Uji tentang kenormalan dimulai pada awal 1900 oleh Karl Pearson (lihat Yazici dan Yolacan, 2007). Selanjutnya beberapa dekade setelah itu banyak peneliti mengembangkan statistik uji untuk uji kenormalan.

2.1 Uji Kenormalan Berdasarkan Fungsi Distribusi Empiris

Uji fungsi distribusi empiris, disebut pula uji jarak (distance test), berdasarkan perbandingan antara fungsi distribusi empiris Fn (xi) = i / n dan

distribusi hipotesis di bawah kenormalan Z_i yang biasanya didefinisikan sebagai

Z₁ =φ{ x x ^ (1)

k s )

dengan x dan s masing-masing menyatakan rata-rata sampel dan simpangan baku sampel (lihat Dufour, et al. 1998; Lee, 1998). Secara umum uji fungsi distribusi empiris terbagi atas dua kelompok (Lee, 1998). Pertama, uji yang melibatkan supremum seperti uji Kolmogorov-Smirnov. Kedua, uji yang menghitung kuadrat perbedaan seperti uji Cramér-von Mises. Berikut akan diberikan uji-uji yang termasuk ke dalam kedua kelompok tersebut beserta modifikasinya.

Cramér (1928) mengusulkan statistik uji

VM = ∑n=i [z‘ - (2i — 1)/2n]² +¹ /(¹2n), (2)

dengan z_i = Φ(e;_in / s), i = 1, k , n; e:_in adalah statistik terurut sisaan dan s = [(n - k)~¹∑"=_ι e² ] ^1/2. Statistik uji (2) disebut pula statistik uji Cramér-von Mises. Selanjutnya, Watson (lihat Stephens, 1972) memodifikasi statistik Cramér-von Mises pada persamaan (2) dan mengusulkan statistik

W = VM² - n(z -1/2)², (3)

dengan z = (1/ n)∑"=₁ zi.

Uji fungsi distribusi empiris selanjutnya diusulkan oleh Kolmogorov (1933) dengan statistik uji berikut:

D⁺ = max[(i / n) - z i ], 1 ≤ i ≤ n;

D^- = max[ z i - (i -1)/ n ], 1 ≤ i ≤ n; ⁽⁴⁾

D = max( D⁺, D^- );

dengan zˆ_i menyatakan distribusi normal standar dan n menyatakan jumlah sampel. Nilai-nilai kritis untuk uji Kolmogorov-Smirnov dapat dilihat pada Kolmogorov (1933).

Kemudian Anderson dan Darling (1952, 1954) mengusulkan statistik uji

AD = - n^-1 ∑i=₁(2 i-1)[ln zi+ ln(1 - z n ^)] - n, (5) dengan z_i menyatakan peluang normal standar (lihat juga Yacizi dan Yolacan, 2007; Stephens, 1972; dan

Dufour et al. ,1998). Hipotesis nul akan ditolak apabila statistik uji (5) lebih dari 2,492 (lihat Yazici dan Yolacan, 2007).

Ajne (1968) mengusulkan statistik uji

AJ=(n /4)^- (²/ n )∑n=₂ ∑j=1 m _ιj (⁶)

dengan nilai m_j = xj -xi, jika χ_j -xi ≤ 1/2;

m_j = 1 -(x_j -xi) jika χ_j -xi > 1/2 .

Selanjutnya akan dibahas beberapa modifikasi terhadap statistik Kolmogorov-Smirnov.

2.1.1 Beberapa modifikasi terhadap statistik Kolmogorov-Smirnov dan Lilliefors

Kuiper (1962) memodifikasi statistik Kolmogorov-Smirnov pada persamaan (4), dengan statistik

V = D⁺ + D^-. (7)

Selanjutnya modifikasi terhadap statistik Kuiper pada persamaan (7) dilakukan oleh Stephens (1970) dengan mengusulkan statistik

V* = V( n^1/2 + 0,155 + 0,24n "^1/2). (8)

Untuk menolak hipotesis nol, statistik uji pada persamaan (8) dibandingkan dengan 1,747 (lihat Yazici dan Yolacan, 2007).

Lilliefors (1967) mengamati bahwa jika satu atau lebih parameter harus diestimasi maka uji tabel standar Kolmogorov-Smirnov tidak lagi berlaku. Selanjutnya Lilliefors (1967) mengusulkan statistik uji

D* = max| F*(x) - Sn(x) |, (9)

x

dengan F^* (x) menyatakan fungsi distribusi normal kumulatif dengan nilai tengah μ = x serta varians σ² = s² dan S_n (x) menyatakan fungsi distribusi kumulatif sampel. Secara paralel van Soest juga memodifikasi statistik Kolmogorov-Smirnov (lihat Molin dan Abdi, 1998; Abdi dan Molin, 2007). Modifikasi lain statistik uji Kolmogorov-Smirnov dilakukan oleh Stephens (1970) dengan statistik

V* = D( n^1/2 + 0,12 + 0,11 n "^1/2), (10)

dengan D menyatakan statistik Kolmogorov-Smirnov. Untuk menolak hipotesis nol nilai pada persamaan (10) dibandingkan dengan 1,358 (lihat Yazici dan Yolacan, 2007).

Drezner et al. (2008) juga memodifikasi statistik Kolmogorov-Smirnov dan mengusulkan statistik D(μ,σ) dengan vektor (μ, σ) adalah solusi yang meminimunkan masalah

min[ D (μ ,σ)], (11)

μ,σ

dengan

D (μ ^,σ) = max[n-^{- φ}('F J ^φ('F)^-^k^-¹1 i ≤ k ≤ n

Nilai-nilai kritis untuk statistik (11) dapat dilihat pada Drezner et al. (2008).

Arcones dan Wang (2005) mengusulkan perbaikan terhadap statistik uji Lilliefors dengan mengenalkan dua uji berdasarkan proses-U, yaitu ~

statistik D_n_,_m dan statistik D_n_,_m . Statistik D_n_,_mdidefinisikan sebagai

= E(X - μ)⁴ = E(X - μ)⁴= [E(X-μ2)²]² = σ⁴

D

n,m

= sup

t ∈ R

(n - m)!

n!

∑I(d∙ ≤ t)-Φ(t)

, (12)

⁽i 1, K,ⁱm )∈ Im

dengan nilai d * = σ_n^mm^l12 ∑ m=₁(X_ij^- Xn ) ^,

dari distribusi N(0,1) adalah 0 dan 3. Konsep momen ini dimunculkan pertama kali oleh Karl Pearson. Selanjutnya, momen ketiga disebut kepencongan (skewness) dan momen keempat disebut kurtosis. Dengan demikian penyimpangan dari kenormalan dapat diketahui dari nilai momen-momen yang diduga menggunakan sampel, yakni koefisien kepencongan b₁ dan koefisien kurtosis

b₂ yang dihitung sebagai

¹"m = ^{(i1K; im ) ∈ Nm ^:1 ≤ ij≤ ⁿ^,ⁱj≠ ik } ^jika

j ≠ k

dan

m₃(m2)^3/2

‘" m^)! Σ m^- (∑' (X, ~ X, )f.

=Λ ⁱj n

n! (<.., im )∈ Im

^b2 =

m₄(m₂)²

(18)

(19)

Menurut Arcones dan Wang (2005) hipotesis nol akan ditolak apabila untuk 0 < α < 1, nilai statistik

U^ji Dn,m > bn,m,α dengan

dengan m j = (1/ n )∑ in (x_i - x )^j . Kepencongan

bnmα = ιnf{Λ≥ 0: ∣Φ{Dnm < λ} ≥ 1 - α}.

~

Selanjutnya statistik D_n_,_m didefinisikan sebagai

_~

D

n,m

= sup

t ∈ R

∑I(d** ≤ t)-d*** ≤ t, (13)

(i_1, K,i_m )∈I_m

dengan nilai d = m ^1/2 ∑,=₁( Xj — X_n) dan nilai

d ** = n ¹∑ n=₁1 (Xj — X_n). Untuk statistik uji

dan kurtosis dapat diukur dengan lebih dari satu cara. Salah satu ukuran kurtosis diusulkan oleh Geary (1947). Untuk pembahasan lebih lanjut tentang kepencongan dan kurtosis lihat DeCarlo (1997) dan Doric et al. (2009).

Uji-uji berdasarkan momen biasanya bersifat omnibus, artinya mampu memberikan informasi tambahan tentang ketidaknormalan distribusi alternatif melalui nilai kepencongan dan kurtosis (lihat Poitras, 2006).

Uji berdasarkan momen pertama kali diusulkan oleh Geary (1947) dengan statistik uji

persamaan (13), hipotesis nol akan ditolak apabila

~

D_n >C ^c_ntna dengan n , im n , im,

c.rn,„ = ιnf{λ ≥ 0: Pφ{D,,,m < λ} ≥ 1 - α}. (14)

a (c ) =

n-¹∑/,∣

1 i=1

x_i

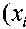
- x |

/2 ,

(20)

2.1.2 Beberapa Modifikasi Terhadap Statistik Ajne

Stephens (1970) memodifikasi statistik yang diusulkan Ajne dengan statistik

AJ* = [AJ - (0,7/ n) + (0,9 / n ²)][1 + (1,23 / n)]. (15) Selanjutnya untuk menolak hipotesis nol statistik uji ini dibandingkan dengan 0,656 (lihat Yazici dan Yolacan, 2007).

dengan x menyatakan rata-rata sampel dan c adalah bilangan real taknegatif.

D’Agostino dan Pearson mengusulkan statistik uji menggunakan momen Pearson (lihat D’Agostino et al., 1990)

K² = Z² (√bT)+ Z² (b2), (21)

yang berdistribusi χ ²(2). Pada persamaan (21) nilai Z² ("Jb) dan Z² (b ₂) adalah pendekatan-pendekatan

normal terhadap b₁ dan b₂ .

2.2 Uji Kenormalan Berdasarkan Momen

Konsep uji berdasarkan momen adalah bahwa momen ketiga dan momen keempat yang diberikan oleh

Pendekatan pengujian menggunakan kepencongan b₁ dan kurtosis b₂ juga diusulkan

oleh Jarque dan Bera (1980, 1987) dan Bera dan

Jarque (1981) dengan statistik uji

E(X - μ)³ _ E(X - μ)²

[E(X -^2)²]^3/2 = σ³

(16)

JB = n

W ₊ (b2 - 3)²

6 24

(22)

Statistik JB secara asimtotis berdistribusi χ² (2). Hipotesis nol akan ditolak apabila statistik JB lebih besar daripada nilai χ² (2).

Hosking (1990) mengusulkan statistik uji berdasarkan momen-L. Misalkan X_i_:_n menyatakan statistik terurut tingkat ke-i dari suatu sampel berukuran n. Definisikan

Statistik pertama yang diusulkan Desmoulins-Lebeault (2004) untuk alternatif kepencongan positif adalah

∆1 = (d 1²/ σss) + (d 2²/ σsk). (28)

Untuk alternatif kepencongan negatif, statistik yang diusulkan adalah

λ = (1/2)E(X2:2 - X₁J, λ₃ = (1/3)E(X_3:3 - 2X_2:3 + X_1:3).

(23)

Kepencongan-L didefinisikan sebagai T₃ = λ₃/ λ₂. Menurut Hosking (1990) statistik

[(0,1866n ¹ + 0,8n ²)'2∣τ (24)

berdistribusi normal.

Bontemps dan Meddahi (2002) mengusulkan model berdasarkan momen rampat (generalized method of moments). Misalkan suatu sampel x₁ ,K, x_n dari peubah acak X . Amatan ini bisa bebas atau tidak bebas. Diasumsikan distribusi

^A2 = ⁽^d3 / ^σss ) ⁺⁽^d42/ ^σsk ).

Selanjutnya statistik ketiga

A3 = ^(max^(| m+ |,| m |) ^- d5⁾² (^σss ) 1 ⁺^(max(|^m4 |,| ^m^- |) ^- d6)2(^σskΓ1.

(29)

(30)

Menurut Desmoulins-Lebeault (2004) distribusi pengambilan sampel pasti dari distribusi semimomen tersebut belumlah diketahui. Oleh karena itu

Desmoulins-Lebeault (2004) menyediakan tabel nilai kritis untuk masing-masing ukuran sampel.

Lobato dan Velasco (2004) mengusulkan statistik kepencongan dan kurtosis rampat untuk data berkorelasi yakni

marjinal X adalah N(0,1) . Misalkan f₁,K, f_padalah fungsi terdiferensialkan sedemikian hingga f_i terdeferensialkan. Untuk setiap bilangan real x ∈ Rp dengan komponen (f_i (x) - xf (x)) untuk i = 1, k , p . Didefinisikan matriks

∑ = ∑+LE [ g (x) g (x-h) T ]• (25) dan misalkan pula

a = n~^1l2∑n=₁g(x) → N(0,∑). (26) Bontemps dan Meddahi (2002) mendefinisikan statistik uji

a^τΣ^-¹ a ~ χ²(p). (27)

Desmoulins-Lebeault (2004) mengusulkan tiga statistik uji berdasarkan metode semi-momen. Misalkan m- menyatakan penduga semi-

_c= nμ3 n(/Z4 - 3∕z₂)²

6 F<³ 24 F⁽⁴⁾

(31)

^dengaⁿ F⁽^k) = ∑ ”J__n ^γ( J)^k^dan

^Y⁽k) = n ¹ ∑^1j^{l (}^xt ^-^x)(xt+∣j∣ ^-^x) .

Rana et al. (2009) mengusulkan uji momen diskala ulang tangguh (robust rescaled moment test) dengan statistik uji

3

RRM = — B1 l

²

Jn J

4 Λ \

+ ⁿcΓ T -³

B 2 l Jn J

(32)

kepencongan kiri, m4 menyatakan penduga semikurtosis kanan, dan n adalah banyaknya amatan sampel yang diuji dan definisikan:

d ₁ = m3 + [ n /(n +1)](2/π)¹2,

∑n

_i=₁∣ x_i -med(xi)|, A = (π/2)^1/2, m₃ adalah momen sampel tingkat ketiga, mˆ ₄ adalah momen sampel tingkat keempat, med(x_i) adalah median sampel, nilai B₁ dan B₂diperoleh dari simulasi Monte Carlo. Untuk tingkat signifikansi α = 0,05, Rana et al. (2009) merekomendasikan B₁ = 6 dan B ₂ = 64.

2.2.1 Beberapa modifikasi uji statistik Geary

d₂ = m₄⁺- [(n -1)/(n +1)](3∕2),

d ₃ = m₃⁺- [ n /(n +1)](2/π)¹/²,

d₄ = m^₄^-- [(n -1)/(n +1)](3/2),

d ₅ = [ n /(n +1)](2/π)¹/²,

d₆ = [(n -1)/(n +1)](3/2), σ_ss = 1,743795n^-¹ -10,062152n “², σ_sk = 21,558373n ¹ - 209,049576n .

Bonnet dan Seier (2002) mengusulkan dua uji omnibus menggunakan ukuran momen Geary, yaitu

G. = [z (JbJf + (z. )2 (33)

dan

G. = a (Jb )f + (-z J² (34)

dengan a = n /[(n -2)^6/(n +1)],

^τ = ⁿ∑n=1^l^xi^-^x^l^,^σ = ⁿ∑n=₁(^xi^-^x)²^,

ω = 13,29(lnσ - lnτ), dan

Zw = (n + 2)¹'²(ω - 3)∕3,54. (35) Hipotesis nol akan ditolak jika statistik uji I zw l> zα/2 .

Cho dan Im (2002) memodifikasi statistik uji Geary dengan mengambil dua momen sampel pertama sm_j , yakni

smj = (1 / n)∑n=₁1 sgn(x - x)(x - x)^j ∣, (36) untuk j = 1,2,3, κ.; selanjutnya jika dimisalkan aj = smj / σ^j, j = 1,2, k akan diperoleh statistik

G = n

(α₁ - (2/^)¹'²)² a 2

. (1 - (3/ π)) ⁺ (3 - (8/π)) _

. (37)

Dalam kondisi kenormalan, statistik G mendekati distribusi χ 2(2) seiring dengan membesarnya

ukuran sampel.

Urzúa (2007) mengusulkan dua uji omnibus untuk kenormalan menggunakan ukuran kepencongan Pearson dan kurtosis Geary, yakni statistik

U1 =

de

dan

U2

f

= max k

bb↑ (w - 3)

d ’ Te J

(38)

(39)

dengan d = 6(n - 2) /[(n +1)(n + 3)],

1^ = (w₁, k , Iwk) adalah penduga dari nilai tengah asimtotik w = (w₁, k , w_k ). Statistik

BHS = n(ι^ - w)T Σ_k¹ (ι^ - w)~ χ²(k), (41) dengan Σ_k adalah matriks kovarians dari distribusi bersama ukuran kepencongan dan kurtosis.

Chen dan Kuan (2003) mengusulkan versi uji JB rampat untuk normalitas bersyarat, yakni fungsi nilai tengah bersyarat berisi intersep tetapi tidak bergantung kepada galat masa lalu dan galat bersyarat bersifat heteroskedastik. Statistik yang diusulkan Chen dan Kuan (2003) adalah

CH = n[Sn Kn - 3]Σn¹[Sn Kn - 3]T, (42) dengan n menyatakan banyak sampel, Sn = n ¹ ∑^ , Kn = n^-¹ ∑^, dan ∑n¹adalah penduga konsisten matriks varians-kovarians asimtotik.

Bai dan Ng (2005) mengembangkan uji JB untuk deret waktu atau data tidak bebas. Statistik yang diusulkan Bai dan Ng (2005) adalah

π₃₄ = π₃ + π₄. (43) Pada persamaan (43) nilai π₃ = (n^1l2∕^₃)/s(/Z₃), π₄ = π₄(3) = (n ^1/2(k- κ))/s(κ), dan s (^ = (βΩΩβ/σ²)¹/².

Stfelec dan Stehlik (2009) mengusulkan kelas statistik tangguh JB yang didefinisikan oleh

e = 3,54/(n + 2), w = -6ln( a )'ln(π /2), dan

₂ 1/2

^a = ∑i=i^l^xi^-^x^{l /[}ⁿ∑”=i⁽^xi ^-^x) ^]

RT = ⅛) (M^j

Ci m α²/, ¹ k i 2,j2 J

+ W f Mij

C2 k Mh.

^-³

J

2.2.2 Beberapa modifikasi statistik uji JB

dengan M_i,j. =⁽¹ ∕ n)∑" =1 φ_j ⁽X_m ^-^m(_i))^,

Urzúa (1996) mengusulkan modifikasi uji Jarque-Bera dengan statistik

JBU =

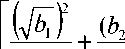
v1)²

v₂ v₃

(40)

i ∈ {0,1} menyatakan rata-rata aritmetika M₀ = X atau median M₁ = M_n, j ∈ {0,1,2,3,4} , dan φ₀ = (π/2)¹'²∣ x |. Selanjutnya φ₁ = x, φ₂ = x², φ₃ = x³, dan φ₄ = x⁴ . Nilai C₁ dan C₂ diperoleh dengan simulasi Monte Carlo (lihat Stfelec dan Stehlík,2009).

Pada persamaan (40) nilai V₁ = 3(n -1)/(n +1), v₂ = 6(n - 2) /[(n +1)(n + 3)], dan

v₃ = 24n(n - 2)(n - 3)/[(n +1)²(n + 3)(n + 5)].

Statistik JBU secara asimtotis juga berdistribusi χ ²(2).

Brys et al. (2004, 2008) mengamati bahwa uji berdasarkan momen memiliki kelemahan apabila data mengandung pencilan. Selanjutnya Brys et al. (2004) mengusulkan bentuk statistik uji JB rampat yang mampu menangai pencilan. Misalkan

2.3. Uji Kenormalan Berdasarkan Korelasi atau Regresi

Konsep dasar uji ini adalah plot peluang normal, yaitu teknik grafik untuk menentukan kenormalan data dengan melihat kelinearan dalam suatu plot dari amatan terurut melawan nilai harapan dari statistik terurut normal standar (Lee, 1998). Selanjutnya untuk menentukan kelinearan dapat digunakan teknik regresi atau teknik korelasi. Jika data normal maka kemiringan akan memberikan nilai simpangan baku

data dan intersep akan memberikan nilai tengah data

(Lee,1998).

melihat kelemahan statistik SW dan mengusulkan statistik

Shapiro dan Wilk (1965) mengusulkan statistik

SW -

⅛ n-₁ ^aiX^ ∑( y- y )²

(44)

∑'-,[i -(n +1)/2]yi n2s

(49)

dengan y_i menyatakan amatan terurut dan s

dengan

T / a mTV^-1

a -(^α,^,K^,an) - (mTv—1v^-1m)_l/²^, (45) mT - (m₁,., m_n) menyatakan vektor nilai harapan

normal standar statistik terurut, V - (v _j) adalah

matriks kovarians n × n , dan y^T — (y₁,κ, U_n)

menyatakan varians sampel.

Modifikasi selanjutnya dilakukan oleh Shapiro dan Francia (1972) yang menyarankan untuk mengabaikan suku kovarians dalam formula untuk mendapatkan berat, yakni memperlakukan amatan terurut seperti halnya saling bebas (lihat juga Dufour et al., 1998; Lee, 1998). Statistik yang diusulkan berbentuk

menyatakan vektor amatan acak terurut. Jika data normal maka statistik SW akan mendekati 1. Namun,

SF -

( n - k) s

(50)

jika data tidak normal maka SW akan lebih kecil daripada 1.

Tiku (1974) mengusulkan statistik yang membandingkan simpangan baku sampel dan

dengan b^T - (b₁,...,b_n) - c^T/(c^Tc)^l/2. Statistik SF

simpangan baku statistik tersensor. Statistik ini dinyatakan sebagai

TI _- (1 - n~ⁱ)σ_c

(1 - (nA )^-¹)σ

(46)

dengan A — 1 — q₁ — q₂, σ adalah simpangan baku

sampel, dan σ_c adalah simpangan baku yang dihitung dari sampel tersensor (lihat Tiku ,1974)

De Wet dan Venter (1972) mengusulkan statistik uji DW berdasarkan koefisien korelasi sampel antara data dan kuantil distribusi normal standar

DW - r²(x, h) (47) dengan r(x,h) adalah koefisien korelasi sampel antar x dan h . Vektor h pada persamaan (47) adalah vektor berdimensi n dengan elemen ke-sama dengan i /(n +1) kuantil distribusi normal standar.

Filliben (1975) mengusulkan statistik uji FI yang dihitung berdasarkan korelasi antar data dan median statistik terurut ke-i, yakni med(x_i )

∑n

FI _- i_-₁ (x_i -x)(med(x_i) -med(x_f))

n

V∑i_-1 (X -x)(med(Xi) -med(Xi))

(48)

2.3.1 Beberapa modifikasi terhadap statistik SW

Bobot yang diusulkan oleh Shapiro dan Wilk (1965) pada statistik uji (44) adalah berat optimal pendugaan kuadrat terkecil rampat dan sulit dihitung (lihat Dufour, et al. 1998). Shapiro dan Wilk (1965) memberikan tabel bobot dan titik-titik signifikan untuk ukuran sampel n ≤ 50. D’Agostino (1971)

mengganti V dengan I pada persamaan (50). Selanjutnya Weisberg dan Bingham (1975) memodifikasi statistik SF dengan mengganti nilai c dengan

ci - Φ

1

i - (3/8) n + (1/4)

i -1,...,n;

(51)

dengan Φ^-¹ menyatakan inversi dari fungsi distribusi kumulatif normal (lihat Dufour et al., 1998; Lee, 1998). Pendekatan ini telah ditunjukkan sesuai untuk sampel kecil.

Sarkadi (1980) mengusulkan untuk melakukan transformasi sebelum menerapkan statistik SW. Lebih lanjut Sarkadi (1980) mengusulkan statistik uji untuk kasus multisampel. Misalkan untuk i -1,., r dan j - 1,k, n_i peubah X_j menyatakan peubah-peubah acak bebas dengan fungsi distribusi F[(X -μ_i)/σ_i] dengan μ_i dan σ_i tidak diketahui.

Untuk kasus homoskedastik, yakni σ₁ - ... - σ_r - σ

dengan ukuran sampel n_i ≥ 2, Sarkadi (1980)

mengusulkan statistik dengan transformasi dua tahap, yakni

Yj- Xj- U₁, dengan

∑ n^-¹ χ_i X

u. - ■ '—-+—in-

‘ ni+ (n)¹/² (ni)^1/2

untuk i -1, k , r dan j -1,., n_i - 2.

melakukan

(52)

(53)

Untuk kasus heteroskedastik dengan ukuran sampel n_i ≥ 3 , Sarkadi (1980) mengusulkan statistik

Y -(X₁- U_i) SY^ ij ij i S

(54)

dengan

U =

y ⁿi^-² x.

Δ-∣ i=1 j

n + (2 n)

+

in_i

-1

in_i

(2ni)^1/2

^,

V_m_,_n(x₁,

, x_n)

S₁= ]∑n=1( Xj- U)² ,

= n 1∑ n=1^log[( n/2 m⁾⁽x (t+m)

, (60) x( i - m)^)]

SYi = Ψ

V

in_i

Si

\

1

m adalah bilangan bulat positif (lihat Baklizi dan Eidous, 2008).

Arizono, et al. (1989) mengusulkan uji entropi berdasarkan entropi Renyi. Entropi Renyi didefinisikan oleh

dengan ψ_n (x) adalah fungsi naik tegas sedemikian

hingga SY ~ (Si /σi)

Chen dan Shapiro (1995) dan Chen (2003) memodifikasi statistik SW dan mengusulkan statistik QH berdasarkan spacing yang dinormalkan, yakni

QH =

¹ yⁿ^-¹^y+ι ^- y t

(n -1) s ∑^t=¹ H_m - Hi’

(55)

dengan H_i =Φ ¹[(i — 3/8)/(n +1/4)], Φ ¹ adalah

inversi distribusi normal standar, s adalah

simpangan baku, dan y_i adalah statistik terurut. Menurut Seier (2002) uji SW memiliki kelemahan apabila terjadi pembulatan terhadap data. Seier (2002) juga menemukan hal yang sama pada statistik QH dan mengusulkan modifikasi dengan bentuk

QH* = (1 - QH) n^1/2. (56)

Coin (2008) memodifikasi statistik SW agar mampu menangani pencilan dengan menggunakan pencarian maju (forward search). Statistik yang diusulkan Coin (2008) adalah

WF= (w_s ,κ,W_s ,κ,W_s ), (57) v S [(n+1)/2] ’ Sk S^n> ^{v 7}

dengan S_k adalah subsampel dari x_LMS yakni penduga regresi kuadrat terkecil dari k amatan pertama.

2.4 Uji Kenormalan Berdasarkan Entropi Sampel

Entropi Shannon dari suatu fungsi distribusi F dengan fungsi densitas peluang f didefinisikan sebagai

f∞

f(x)lnf(x) dx (58)

"

(lihat Arizono et al., 1998; Park dan Park, 2003; Baklizi dan Eidous, 2008; Choi, 2008). Entropi dari 2

distribusi normal dengan varians σ adalah (2πeσ ²)^1/2.

Vasicek (1975) mengusulkan uji entropi sampel dengan statistik uji exp[V (x , K,x )] m,n 1, , n

m,n ,

^σ( x1^,K^, xn )

berdasarkan

(59)

H, (.f) = (1 - /l' ln f_[ f (x)]^γ d■ (61)

dengan / > 0 dan / ≠ 1. Entropi ini disebut entropi tingkat / dari fungsi densitas peluang f. Apabila γ → 0, entropi Renyi akan tereduksi menjadi entropi Shannon. Selanjutnya Arizono, et al. (1989) mengusulkan statistik uji berdasarkan entropi Renyi

1

H,(f) = (1 - /) ln∫_n[- F (P H¹^y dp. (62) 0 dp

Arizono et al. (1989) memperoleh nilai dugaan untuk (62)

//(/-1)

Hmn = ln n^ Σn=₁(x+ m - X₁-m t ^ ] ^1/(1—^^)

Choi (2008) mengusulkan statistik uji untuk entropi sampel yang didefinisikan oleh

H'.- = R h ‘.Z X(t+m) - X(t-m))] '^,!. (64)

Sn-1

dengan

R_m, _n = exp[-(1 - 2 m / n )ψ(2 m) + ψ( n +1)

- 2/n∑m=₁ψ(k + m -1)] ( )

dan Sn-1 = [n/(n -1)]^1/2Sn.

2.5 Uji Kenormalan Berdasarkan Karakterisik Polya

Muliere dan Nikitin (2002) dan Litnova dan

Nikitin (2006) mengusulkan dua statistik uji kenormalan berdasarkan karakteristik Polya. Misalkan fungsi distribusi empiris dinyatakan oleh

Gn (t) = n^- ∑n=₁1{Xt < t}, t ∈ R¹, (66)

dan fungsi distribusi statistik-V dinyatakan oleh Rm, n (t) =

ⁿ^-^m⁽^m^!)^-1 Σ (∑σI^{aσ(⅜)X1 ⁺ L ⁺ aσ(m)^Xm < ^t^}) ^.¹'1 ^,^k^,¹'m=1

Selanjutnya statistik uji yang diusulkan Litnova dan Nikitin (2006) berbentuk

B2,n =∫" [R2,n(t)-Gn(t)]dGn(t) (67)

"

dan

Cm, n =∫"[ Rmn (t) - Gn (t)] d Gn (t )■ m > 2. (68) "

untuk t ∈ R¹.

2.6 Uji Kenormalan Berdasarkan Metode Kernel

wv* *

ii jj

= w⁽²⁾

( v. .* ii

_-

v* jj

l

b

Λ

/

(75)

Ahmad dan Mugdadi (2003) mengusulkan metode kernel untuk menguji kenormalan. Misalkan x₁, K ,x_n adalah sampel acak dari suatu fungsi distribusi F dengan densitas f. Misalkan u_ii* = x_i + x_i* dengan fungsi densitas peluang h₁ dan

2.7 SIMPULAN

v_ii_* = x_i - x_i* dengan fungsi densitas peluang h₂ . Misalkan pula h(u, v) menyatakan densitas bersama *

u dan v untuk semua i ≠ i = 1, K ,n . ii ⁱⁱ^*

Selanjutnya penduga kernel h₁ , h₂ , dan h diberikan

oleh

h₁(u) =

1

n(n -1)b

y..

i≠i

*

( u — u * ii

l b

dan

h^ˆ₂(v) =

1

n(n -1)b

∑

i≠i

*

( v

w

l

h(u, v) =

¹n(n-1)b²ⁱ^≠ⁱ

*

w

-v

ii

-u

ii

b

\

b

√

w

(69)

(70)

v-v ii

√ l

b

√

(71)

dengan b = b_n adalah konstanta positif yang disebut

bandwidth dan w(.) adalah densitas terbatas simetrik yang disebut kernel. Diasumsikan w memiliki nilai tengah 0 dan varians tertentu µ₂ (w) dan b → 0 sebagaimana n → ∞ . Selanjutnya apabila ingin 2

menguji H0 : f adalah N(µ,σ ) melawan

H_a : f bukan N(µ,σ²) maka ukuran δ yang

didefinisikan oleh

i∞ r∞

[h(u,v) - h₁(u)h₂(v)]² du dv, (72)

-∞ -∞

dapat digunakan untuk mengukur kenormalan. Menurut Ahmad dan Mugdadi (2003) δ ≥ 0 dan δ= 0 jika dan hanya jika hipotesis nol benar. Lebih lanjut Ahmad dan Mugdadi (2003) memperoleh dugaan untuk (72)

ˆ¹

n⁴(n - 1)⁴b²

wu_{* *}

i≠i^* j≠ j^* l≠l^* r≠r^* ii jj

[w^v + w^v - 2w^v ]

ii^* jj^* ll^*rr^* ii^*ll^*

dengan

w^u

ii jj

= w⁽²⁾

( u... ii

-u

jj

l

b

√

dan

(73)

(74)

Masing-masing statistik uji kenormalan memiliki keunggulan dan kelemahan masing-masing. Studi komprehensif menunjukkan bahwa uji yang berdasarkan fungsi distribusi empiris secara umum tidak mampu memberikan informasi lain tentang ketidaknormalan. Sebaliknya uji yang berdasarkan momen bersifat omnibus, tetapi tidak terlalu bagus untuk sampel berukuran kecil dan data yang berisi pencilan (lihat Poitras, 2006; Urzúa, 1996; Urzúa, 2007). Uji yang berdasarkan regresi atau korelasi biasanya memerlukan komputasi yang itensif pada saat menentukan bobot. Demikian pula dengan uji-uji yang berdasarkan entropi sampel, kernel, dan karakteristik Polya cenderung memberikan statistik uji yang memerlukan komputasi intensif, terutama simulasi Monte Carlo. Uji kenormalan akan senantiasa berkembang sesuai dengan cara pandang terhadap kenormalan. Sebagai contoh uji kenormalan berdasarkan transformasi proses empiris (Cabaña dan Cabaña, 2003), uji berdasarkan informasi Fisher (Lee, 1998), uji menggunakan statistik Q (Zhang, 1999), dan uji berdasarkan jarak L₂ - Wasserstein (Del Barrio, et al. 1999).

DAFTAR PUSTAKA

Abdi, H. and Molin, P. 2007. Lilliefors/Van Soest’s Test of Normality. In Neil Salkind (Ed.) Encyclopedia of Measurements and Statistics. Thousand Oaks (CA); Sage

Ahmad, I. A. and Mugdadi, A. R. 2003. Testing for Normality Using Kernel Methods. Nonparametric Statistics. 58(3): 273—288.

Ajne, B. 1968. A Simple Test for Uniformity of a Circular Distribution. Biometrika. 55: 343—354.

Anderson, T. W. and Darling, D. A. 1952. Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Process. The Annals of Mathematical Statistics. 23: 193–212.

Anderson, T. W. and Darling, D.A. 1954. A Test of Goodness-of-fit. Journal of American Statistical Association. 49:765—769.

Arcones, M. A. and Wang, Y. 2006. Some New Tests for Normality Based on U-process. Statistics and Probability Letters. 76:69—82.

Arizono, I., Kittaka, A., and Ota, H. 1989. A Test of Normality Based on Generalized Entropy. Bulletin of University of Osaka Prefecture. Series A. Engineering and Natural Sciences. 37(2): 153—160.

Bai, J. and Ng, S. 2005. Tests for Skewness, Kurtosis, and Normality for Time Series Data. Journal of Business and Economic Statistics. 23(1): 49—60.

Baklizi, A. and Eidous, O. 2008. Goodness of Fit Tests for Normality Based on Kernel Entropy Estimators. Bulletin of Statistics and Economics. 2(A08): 19—25.

Bera, A. K. and Jarque, C. M. 1981. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals: Monte Carlo Evidence. Economics Letters. 7: 313—318.

Bonett, D. G. and Seier, E. 2002. A Test of Normality with High Uniform Power. Computational Statistics and Data Analysis. 40: 435—445.

Bontemps, C. and Meddahi, N. 2002. Testing Normality: A GMM Approach. Cahier 2002-14. Alamat https://papyrus.bib.umontreal.ca:8443/dspace/bits tream/1866/485/1/2002-14.pdf diakses tanggal 30 April 2010.

Breton, M. D., Devore, M. D., and Brown, D. E. 2008. A Tool for Systematically Comparing the Power of Tests for Normality. Journal of Statistical Computation and Simulation. 78(7): 623—638.

Brys, G., Hubert, M., and Struyf, A. 2004. A Robustification of the Jarque-Bera Test of Normality. In COMPSTAT’ 2004 Symposium. 753—760.

Brys, G., Hubert, M., and Struyf, A. 2008. Goodness-of-fit Tests Based on a Robust Measure of Skewness. Computational Statistics. 23:429—442.

Cabaña, A. and Cabaña, E. M. 2003. Tests of Normality Based on Transformed Empirical Process. Methodology and Computing in Applied Probability. 5: 309—335.

Chen, L. 2003. C470. Normality Tests Based on Weighted Order Statistics. In Comments, Conjectures, and Conclusion. Section Editor: I. J. Good. Journal of Statistical Computation and Simulation. 73(8): 603—617.

Chen, L. and Shapiro, S. S. 1995. An Alternative Test for Normality Based on Normalized Spacings. Journal of Statistical Computation and Simulation. 53: 269—288.

Chen, Y-T. and Kuan, C-M. 2003. A Generalized Jarque-Bera Test of Conditional Normality. IEAS Working Paper IEAS Institute of Economics, Academia Sinica, Taipei, Taiwan. Alamat http://idv.sinica.edu.tw/ckuan/pdf/jb01.pdf diakses tanggal 30 April 2010, 1—11.

Cho, D. W. and Im, K. S. 2002. A Test of Normality Using Geary’s Skewness and Kurtosis Statistics. Alamat http://www.bus.ucf.edu/wp/content/archives/nor malit.PDF diakses tanggal 30 April 2010.

Choi, B. 2008. Improvement of Goodness-of-fit Test for Normal Distribution Based on Entropy and Power Comparison. Journal of Statistical Computation and Simulation. 78(9):781—788.

Coin, D. 2008. Testing Normality in the Presence of Outliers. Statistical Methods and Applications. 17: 3—12.

Coin, D. and Corradetti, R. 2006 Tests for Normality: Comparison of Powers (Test di Normalità: Confronto delle Potenze). Alamat http://sis-statistica.it/files/pdf/atti/Spontanee2006_177-

180.pdf diakses tanggal 30 April 2010. 177— 180.

Cramér, H. 1928. On the Composition of Elementary Errors. Skandinavsk Aktuarietidskrift. 11: 141— 180.

D’Agostino, R. B. 1971. An Omnibus Test of Normality for Moderate and Large Size Samples. Biometrika. 58(2): 341—348.

D’Agostino, R. B., Belanger, A. and D’Agostino Jr., R. B. 1990. A Suggestion for Using Powerful and Informative Tests of Normality. The American Statistician. 44 (4): 316—321.

De Wet, T. and Venter, J. H. 1972. Asymptotic Distribution of Certain Test Criteria of Normality. South African Statistics Journal. 6: 135—149.

DeCarlo, L. T. 1997. On the Meaning and Use of Kurtosis. Psychological Methods. 2(3): 292—307.

Del Barrio, E. Cuesta-Albertos, J. A., Matrán, C. and Rodríguez- Rodríguez, J. M. 1999. Tests of Goodness of Fit Based on the L2 Distance. The Annals of Statistics. 27(4): 1230—1239.

Desmoulins-Lebeault, F. 2004. Semi-moments Based Tests of Normality and the Evolution of Stock Returns Towards Normality. French Finance Association Meeting 16—17 December 2004. BNP—PARIBAS. Paris. Alamat http://www.en.affi.asso.fr/uploads/Externe/36/CT R_FICHIER_108_1226315203.pdf diakses tanggal 30 April 2010.

Doric, D., Nikolic-Doric, E., Jevremovic, V., and Malisic. 2009. On Measuring Skewness and Kurtosis. Qual. Quant. 43: 481—493.

Drezner, Z., Turel, O., and Zerom, D. 2008. A Modified Kolmogorov-Smirnov Test for Normality. Munich Personal RePEc Archive (MPRA) Paper No. 14385. Alamat http://mpra.ub.uni-muenchen.de/14385 diakses tanggal 30 April 2010.

Dufour, J-M., Farhat, A., Gardiol, L. and Khalaf, L. 1998. Simulation-based Finite Sample Normality Tests in Linear Regressions. Econometrics Journal. 1: 154—173.

Farrell, P. J. and Rogers-Stewart, K. 2006. Comprehensive Study of Tests for Normality and Symmetry: Extending the Spiegelhalter Test. Journal of Statistical Computation and Simulation. 76(9): 803—816.

Filliben, J. J. 1975. The Probability Plot Correlation Coefficient Test for Normality. Technometrics. 17(1): 111—117.

Geary, R. C. 1947. Testing for Normality. Biometrika. 34(3/4):209—242.

Hosking, J. R. M. 1990. L-moments: Analysis and Estimation of Distributions using Linear Combination of Order Statistics. Journal of the Royal Statistical Society, Series B. 52: 105—124.

Jarque, C. M. and Bera, A. K. 1980. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals. Economics Letters. 6. 255—259.

Jarque, C. M. and Bera, A. K. 1987. A Test for Normality of Observations and Regression Residuals. International Statistical Review. 55(2):163—172.

Kolmogorov, A. N. 1933. Sulla Determinazione Empirica di Une Legge di Distribuzione. Giornale dell’Intituo Italiano degli Attuari. 4: 83—91.

Koziol, J. A. 1986. Relative Efficiencies of Goodness of Fit Procedures for Assessing Univariate Normality. Annals of the Institute of Statistical Mathematics. 38(Part A): 485—493.

Kuiper, N. H. 1962. Test Concerning Random Points on a Circle. Proceedings of the Koninklijks Nederlandse Akademie van Wetenschappen, Series A. 63. 38—47.

Lee, Y-H. 1998. Fisher Information Test of Normality. PhD Thesis. Virginia Polytechnic Institute and State University.

Litvinova, V. V. and Nikitin, Y. Y. 2006. Two Families of Normality Tests Based on Polya-Type Characterization and Their Efficiencies. Journal of Mathematical Sciences. 139(3): 6582—6588.

Lilliefors, H. W. 1967. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. Journal of the American Statistical Association. 62(318): 399—402.

Lobato, I. N. and Velasco, C. 2004. A Simple Test of Normality for Time Series. Econometric Theory. 20. 671—689.

Lumley, T., Diehr, P., Emerson, S., and Chen, L. 2002. The Importance of the Normality Assumption in Large Public Health Data Sets. Annual Review of Public Health. 23: 151—169.

Molin, P., and Abdi, H. 1998. New Tables and Numerical Approximation for the Kolmogorov-Smirnov/Lilliefors/Van Soest Test of Normality. Technical Report University of Bourgogne. Alamat

http://www.utd.edu/~herve/MolinAbdi1998-LillieforsTechReport.pdf diakses tanggal 30 April 2010.

Muliere, P. and Nikitin, Y. 2002. Scale-invariant Test of Normality Based on Polya’s Characterization. Metron. 60 (1-2): 21—33.

Park, S. and Park, D. 2003. Correcting Moments for Goodness of Fit Tests Based on Two Entropy Estimates. Journal of Statistical Computation and Simulation. 73(9): 685—694.

Poitras, G. 2006. More on the Correct Use of Omnibus Tests for Normality. Economic Letters. 90:304— 309.

Rana, M. S., Midi, H., and Rahamtullah, A.H.M. 2009. A Robust Rescaled Moment Test for Normality in Regression. Journal of Mathematics and Statistics. 5(1): 54—62.

Sarkadi, K. 1980. Testing for Normality. Mathematical Statistics Banach Center Publications. 6: 281— 287.

Seier, E. 2002. Comparison of Tests for Univariate Normality. InterStat. Alamat http://interstat.statjournals.net/YEAR/2002/article s/0201001.pdf diakses tanggal 30 April 2010.

Shapiro, S. S. and Francia, R. S. 1972. An Approximate Analysis of Variance Test for Normality. Journal of the American Statistical Association. 67:215— 217.

Shapiro, S. S. and Wilk, M.B. 1965. An Analysis of Variance Test for Normality (Complete Samples). Biometrika. 52(3/4): 591—611.

Stephens, M. A. 1970. Use of Kolmogorov-Smirnov, Cramér-von Mises and Related Statistics without Extensive Tables. Journal of Royal Statistical Society, Series B. 32(1): 115—122.

Stephens, M. A. 1972. EDF Statistics for Goodness-of-Fit: Part I. Technical Report No. 186. Stanford University California.

Strelec, L. and Stehlik, M. 2009. On Robust Testing for Normality. Proceedings of the Sixth St. Petersburg Workshop on Simulation. 755—759.

Tanweer-ul-Islam. 2008. Normality Testing—A New Direction. Munich Personal RePEc Archive (MPRA) Paper No. 16452. Alamat http://mpra.ub.uni-muenchen.de/16452 diakses tanggal 30 April 2010.

Tanweer-ul-Islam and Zaman A. 2008. Normality Testing—A New Direction. Alamat http://www.economics.smu.edu.sg/femes/2008/C S_info/papers/418.pdf diakses tanggal 30 April 2010.

Thadewald, T. and Büning, H. 2007. Jarque-Bera Test and Its Competitors for Testing Normality—A Power Comparison. Journal of Applied Statistics. 34(1): 87—105.

Tiku, M. L. 1974. Testing Normality and Exponentiality in Multi-sample Situations. Communications in Statistics. 3(8): 777—794.

Urzúa, C. M. 1996. On the Correct use of Omnibus Tests for Normality.Econometric Letters.53: 247—251.

Urzúa, C. M. 2007. Portable and Powerful Tests for Normality. Latin American Meeting of the Econometric Society. Universidad de los Andes. Bogotá. Colombia. Octubre. Internacional. Alamat http://www.webmeets.com/files/papers/LACEA-LAMES/2007/591/Portable.pdf diakses tanggal 30 April 2010.

Vasicek, O. 1975. A Test for Normality Based on Sample Entropy. Journal of the Royal Statistical Society, Series B, 38: 54—59.

Weisberg, S. and Bingham, C. 1975. An Approximate Analysis of Variance Test for Non-normality Suitable for Machine Calculation. Technometrics. 17: 133—134.

Yazici, B. and Yolacan, S. 2007. A Comparison of Various Tests of Normality. Journal of Statistical Computation and Simulation. 77(2): 175—183.

Zhang, P. 1999. Omnibus Test of Normality Using the Q Statistic. Journal of Applied Statistics. 26(4): 519—528

MODEL PENYERAPAN OBAT UNTUK INTERVAL DAN DOSIS BERBEDA

I NYOMAN WIDANA

Jurusan Matematika, FMIPA, Universitas Udayana Email: [email protected]

INTISARI

Pada artikel ini akan dibahas akumulasi jumlah obat dalam aliran darah untuk dua metode pemberian obat. Metode pertama obat diberikan setiap 12 jam dengan dosis 12,5 mg, sedangkan metode kedua obat diberikan setiap 24 jam dengan dosis 25 mg. Hasil perhitungan menunjukkan bahwa metode kedua menghasilkan akumulasi jumlah obat dalam aliran darah yang lebih banyak daripada metode pertama.

Kata kunci: penyerapan obat, dosis obat, akumulasi jumlah obat.

DRUG ABSORPTION MODEL FOR DIFFERENT INTERVALS AND DOSES

I NYOMAN WIDANA

Mathematics Department, FMIPA, Udayana University Email: [email protected]

ABSTRACT

This article will discuss the accumulated quantity of the drug in the bloodstream of the two administered methods of the drug. The first method the drug is administered every 12 hours with a dose of 12.5 mg, whereas for the second method the drug is administered every 24 hours with a dose of 25 mg. The calculations show that the second method accumulates more drugs in the bloodstream than the first method. SDFLSDKFLSDFSLKFLSKJFSKFLSKFKSDFLKJSLFSLKFSLKFLSKFSLKFLS

Keywords: drug absorption, drug dose, drug accumulation.

1. PENDAHULUAN Misalkan y = y(t) menyatakan jumlah obat

Dokter kadang-kadang memberi pilihan kepada pasien untuk meminum obat dua kali sehari dengan dosis tertentu atau satu kali sehari dengan dosis dua kalinya. Untuk itu dalam tulisan ini akan dibahas jumlah obat dalam aliran darah untuk kedua pilihan tersebut.

Tujuan penulisan makalah ini adalah untuk mengetahui akumulasi jumlah obat dalam aliran darah untuk pemberian obat dengan jangka waktu yang lama, khususnya, untuk dua metode pemberian obat. Metode pertama obat diberikan setiap 12 jam dengan dosis 12,5 mg. Sedangkan untuk metode kedua, obat diberikan setiap 24 jam dengan dosis 25 mg. Selain itu akan dibandingkan akumulasi jumlah obat untuk berbagai kecepatan penyerapannya.

2. TINJAUAN PUSTAKA

Studi tentang penurunan konsentrasi obat dalam darah merupakan hal yang vital bagi pasien. Respon dari pasien terhadap dosis obat yang diberikan sangat menentukan dosis yang diperlukan dan interval waktu pemberian obat.

dalam aliran darah pada saat t . Asumsikan laju perubahannya sebanding dengan konsentrasi obat dalam aliran darah. Hal ini dapat dimodelkan sebagai persamaan diferensial berikut (lihat Burghes dan Borrie,1981; William, 1983)

dy = - ky (1)

dt

dengan k adalah konstanta positif yang nilainya dapat ditentukan berdasarkan hasil eksperimen terhadap obat yang diteliti.

Misalkan pasien diberikan dosis awal sebesar y₀dan diasumsikan langsung diserap oleh darah pada t = 0, maka hal ini mengakibatkan y = y₀ pada saat t = 0. Waktu sebenarnya yang diperlukan untuk penyerapan obat biasanya sangat singkat dibandingkan dengan waktu untuk pemberian dosis berikutnya. Solusi umum dari persamaan (1) adalah y = y 0e^-^kt. (2)

Setelah waktu yang ditentukan, misalkan T, dosis kedua sebesar y₀ diberikan kepada pasien.

Sesaat sebelum dosis ini diberikan, yaitu pada saat t = T-, jumlah obat dalam darah adalah

y (T- ) = yoe-^kT.

Sesaat setelah dosis kedua ini diberikan, pada waktu T = T₊ maka

y (T+) = y o + y oe^-kT = y 0(1+e^-^kT).

Jumlah obat ini menyusut sesuai dengan persamaan (1) dengan kondisi awal y = y₀(1 + e^-^kT) pada saat t = T. Sehingga untuk t ≥ T dengan mengingat persamaan (1), diperoleh

y (t) = y 0(1 + e^-^kT )e^-^k⁽^t^- T). (3)

Sehingga, untuk t → 2T

y (2T- ) = y 0(1 + e^-^kT )e^-^kT.

Selanjutnya setelah memberikan pasien dosis y₀pada waktu t = 2T diperoleh

y (2T+ ) = y 0(1 + e^-^kT + e^-2^kT )

dan sekali lagi dengan menggunakan persamaan (1) dengan y = y₀(1 + e“^kT + e^-2^kT ) pada saat t = 2T, diperoleh

y(t) = y₀(1 + e^-^kT + e^-2^kT )e^-^k⁽^t^-2^T), untuk t ≥ 2T.

Dengan jalan yang sama,

y (3T- ) = y 0(1 + e^-^kT + e^-2^kT )e^-^kT,

dan setelah diberi dosis y = y₀ pada t = 3T ,

y (3T₊ ) = y ₀(1 + e^-^kT + e^-2^kT + e^-3^kT ).

Selanjutnya, diperoleh

y (nT₊ ) = y ₀(1 + e^-^kT + e^-2^kT + e^-3^kT + l + e^-^nkT ), untuk n = 1,2, k .

Kemudian menggunakan deret geometri diperoleh

y⁽ⁿT+) =

y 0(1 - e⁽ⁿ^-¹⁾^kT) 1-e^-kT

dan untuk n yang makin besar, diperoleh

y (nT+) → ₁^y

Dari model ini diperoleh bahwa jumlah obat dalam darah akan mencapai tingkat kejenuhan, y_j dengan

y =

y₀1-e^-kT

(4)

3. PENYERAPAN OBAT

Misalkan pasien diberikan obat dengan dosis 12,5 mg setiap 12 jam (1/2 hari) maka, dari persamaan (2), diperoleh jumlah obat dalam darah adalah

y = 12,5e^-^kt, 0 ≤ t ≤ ⅜.

Berdasarkan persamaan (3), diperoleh y1(t) = y01(1 + e^-^kT )e^-^k⁽^t^-T), ⅜ ≤ t < 1.

Sedangkan untuk pengobatan dengan dosis 25 mg setiap 24 jam (1 hari) diperoleh

y ₂ = 25e^-^kt, 0 ≤ t ≤ 1.

Untuk k = 1, jumlah obat dalam darah untuk dosis

12,5 mg dan 25 mg diilustrasikan oleh grafik berikut

Gambar 1. Jumlah obat dalam aliran darah untuk k = 1.

Sedangkan untuk k = 5 , jumlah obat dalam darah dapat dilihat pada grafik berikut

Gambar 2. Jumlah obat dalam aliran darah untuk k = 5.

Selanjutnya akan dibahas jumlah obat dalam aliran darah dalam jangka waktu yang lama untuk kedua metode diatas. Metode 1, pasien diberikan obat dengan dosis 12,5 mg setiap 12 jam (1/2 hari), maka jumlah obat dalam darah dalam jangka waktu yang lama, dengan menggunkan persamaan (4), akan mencapai

12,5

^yj¹ 1 p-k/2 . (⁵)

1 e

Untuk metode 2, pengobatan dilakukan dengan dosis 25 mg setiap 24 jam (1 hari), sehingga dengan jalan yang sama diperoleh

yj2 =

25

1 - e^-^k^.

(6)

Jumlah obat dalam darah untuk kedua metode tersebut, untuk 1 ≤ k ≤ 5, diilustrasikan oleh grafik berikut

---------- Metode 1

^a Metode 2

Gambar 3. Jumlah obat dalam aliran darah untuk 1 ≤ k ≤ 5.

Selanjutnya, dapat ditunjukkan bahwa

12,5 25

y,i =-----■ <-----r = y i 2, untuk k > 0.

j¹ 1 - e^-^k/2 1 - e^-^k j ²

Hal ini berarti bahwa dalam jangka waktu yang lama, jumlah obat dalam aliran darah, untuk metode 1, lebih sedikit dari jumlah obat dalam aliran darah untuk metode 2.

4. SIMPULAN

Pemberian obat setiap 24 jam dengan dosis 25 mg menghasilkan akumulasi jumlah obat dalam aliran darah yang lebih banyak daripada pemberian obat setiap 12 jam dengan dosis 12,5 mg, untuk pemberian obat dengan jangka waktu yang lama.

DAFTAR PUSTAKA

Burghes, D. N. and Borrie, M. S. 1981. Modelling with Differential Equation. Ellis Horwood Limited. London.

William, F. L. 1983. Differential Equation Models. Springer-Verlag. New York.

IMPLEMENTASI BEBERAPA UJI KENORMALAN OMNIBUS DENGAN PERANGKAT LUNAK R

I WAYAN SUMARJAYA

Jurusan Matematika, FMIPA, Universitas Udayana Email: [email protected]

INTISARI

Uji kenormalan omnibus adalah ujian kenormalan yang mampu memberikan informasi tambahan tentang ketidaknormalan data atau penyimpangannya melalui koefisien kepencongan dan kurtosis. Penelitian ini bertujuan untuk mengimplementasikan penghitungan statistik uji kenormalan omnibus D’Agostino-Pearson K² dan statistik uji modifikasi Jarque-Bera menggunakan perangkat lunak R.sfdsdfsfsfsdfs sdfdsfsfssfsfsdfsd dfsdllflsdflskdflsklfkslfksdllskflskflsllsdfs

Kata kunci: uji kenormalan omnibus, uji D’Agostino-Pearson, uji Jarque-Bera termodifikasi.

IMPLEMENTATION OF SOME OMNIBUS NORMALITY TEST USING R SOFTWARE

I WAYAN SUMARJAYA

Mathematics Department, FMIPA, Udayana University Email: [email protected]

ABSTRACT

An omnibus normality test is a normality test that can give additional information about nonnormality or other deviation from normality through the skewness and the kurtosis coefficients. The aim of this research is to implement the omnibus D’Agostino-Pearson K² test and modified Jarque-Bera test statistic using R software. ssdkflsfjlskdflskjflskflskflskflskfksflksjfkslfksfksfslkfslkfslfsfsfssss.sdflsfl

Keywords: omnibus normality test, D’Agostino-Pearson test, modified Jarque-Bera.

1. PENDAHULUAN

Uji kenormalan telah menarik banyak perhatian para peneliti. Telah ratusan tulisan ilmiah tentang uji kenormalan dipublikasikan. Secara umum uji kenormalan dapat dikelompokkan ke dalam beberapa jenis: uji berdasarkan fungsi distribusi empiris, uji berdasarkan momen, uji berdasarkan korelasi atau regresi, uji berdasarkan entropi sampel, uji berdasarkan karakteristik Polya, uji berdasarkan metode kernel, dan uji berdasarkan metode nonparametrik.

Studi komprehensif yang dilakukan Stephens (1972), Koziol (1986), Dufour et al.(1998), Seier (2002), Coin dan Corradetti (2006), Farrell dan Rogers-Stewart (2006), Breton et al. (2008) Yazici and Yolacan (2007), Tanweer-ul-Islam (2008), Tanweer-ul-Islam dan Zaman (2008) menunjukkan bahwa masing-masing statistik uji memiliki keunggulan dan kelemahan. Sebagai contoh uji yang berdasarkan fungsi distribusi empiris atau uji jarak umumnya tidak mampu memberikan informasi tambahan tentang ketidaknormalan distribusi alternatif. Uji yang berdasarkan regresi atau korelasi

biasanya memerlukan komputasi yang itensif pada saat menentukan bobot. Demikian pula dengan uji-uji yang berdasarkan entropi sampel, kernel, dan karakteristik Polya cenderung memberikan statistik uji yang memerlukan komputasi intensif, terutama simulasi Monte Carlo.

Statistik uji yang mampu memberikan informasi tambahan tentang ketidaknormalan atau penyimpangan dari kenormalan disebut uji omnibus. Uji ini biasanya melaporkan koefisien kepencongan dan kurtosis sebagai ukuran untuk mengetahui normal atau tidaknya data.

Penelitian ini membahas implementasi statistik uji kenormalan omnibus D’Agostino-Pearson K²(lihat D’Agostino, et al. 1990) dan modifikasi uji Jarque-Bera yang diusulkan oleh Urzúa (1996, 2007)

2. METODE-METODE UJI KENORMALAN OMNIBUS

Konsep uji berdasarkan momen adalah bahwa momen ketiga dan momen keempat yang diberikan oleh

_β _ E(X - μ)³ _ E(X - μ)² (1)

'^j1 [E(X -μ2)T² σ^{3 U}

dan

_β _ E(X - μ)4 _ E(X - μ)4

^P2 [ E (X - μ2)²]² σ⁴ °

dari distribusi N(0,1) adalah 0 dan 3. Konsep momen ini dimunculkan pertama kali oleh Karl Pearson. Selanjutnya, momen ketiga disebut kepencongan (skewness) dan momen keempat disebut kurtosis. Dengan demikian penyimpangan dari kenormalan dapat diketahui dari nilai momen-momen yang diduga menggunakan sampel, yakni koefisien kepencongan b₁ dan koefisien kurtosis

b₂ yang dihitung sebagai

b^h = (m') 3/2 ⁽³⁾

(m₂ ) dan

^b2 = (4)

(m₂)²

dengan m_j = (1/ n)∑” (x_i - x)^j.

Kepencongan dan kurtosis dapat diukur dengan lebih dari satu cara. Fisher (lihat D’Agostino et al., 1990) mendefinisikan kepencongan g₁ dan kurtosis g₂ sebagai

g = ⁿ ∑'1(xi^-^x >³ (5)

^S1 (n -1)( n - 2) s³’

dan

= ⁿ(ⁿ +¹)∑"=₁(^xi^-^x⁾⁴ _- 3(n -1)² ₍₆₎

^g² (n -1)(n - 2)(n - 3)s⁴ (n - 2)(n - 3), ⁽ ) dengan

_ yⁿ _ι(x-x)²

s 2 = ∑⅛A----l. (7)

(n -1)

Geary (lihat Bonnet dan Seier, 2002) mendefinisikan kurtosis sebagai τ / σ dengan τ = E(| X - μ |) . Lebih lanjut, menurut Bonnet dan Seier (2002) pada kondisi kenormalan dapat ditunjukkan bahwa τ / σ = (2/^)^1/2= 0,7979. Pembahasan lebih lanjut tentang kepencongan dan

yang berdistribusi χ ²(2) apabila populasi berdistribusi normal. Pada persamaan (8) nilai Z² (∙∖b) dan Z² (b ₂) adalah pendekatan-pendekatan normal terhadap b₁ dan b₂ . Hipotesis dan langkah-langkah pengujian terhadap kepencongan, kurtosis, dan statistik K ² dapat dilihat pada D’Agostino et al. (1990).

2.2 Uji Omnibus Jarque-Bera

Pendekatan pengujian menggunakan kepencongan b₁ dan kurtosis b₂ juga diusulkan oleh Jarque dan Bera (1980, 1987) dan Bera dan Jarque (1981) dengan statistik uji

J^B = n [⁽⁾⁺⁽^b2243) j (9)

Statistik JB secara asimtotis berdistribusi χ2(2). Hipotesis nol akan ditolak apabila statistik JB lebih besar daripada nilai χ² (2).

Urzúa (1996) melihat kelemahan uji Jarque-Bera untuk sampel berukuran kecil sampai menengah dan mengusulkan modifikasi uji Jarque-Bera dengan statistik

JBU =LbI + ⁽^b²^- ^² . (10)

v 2 v3

Pada persamaan (10) nilai

v₁ = 3(n -1)/(n +1),

v₂ = 6(n - 2) /[(n +1)(n + 3)], dan

v₃ = 24n(n - 2)(n - 3)/[(n +1)²(n + 3)(n + 5)].

Statistik JBU secara asimtotis juga berdistribusi X²(2).

Urzúa (2007) mengusulkan dua uji omnibus untuk kenormalan menggunakan ukuran kepencongan Pearson dan kurtosis Geary, yakni statistik

U1 = UbL + C^-³² (11)

de

dan

kurtosis dapat dilihat pada DeCarlo (1997).

2.1 Uji Omnibus D’Agostino-Pearson K²

U2 = max _r ) . (12)

I d ee )

Pada persamaan (11) dan (12) nilai

D’Agostino dan Pearson mengusulkan statistik uji menggunakan momen Pearson (lihat D’Agostino et al., 1990)

K² = Z² (√b)+ Z² (b2), (8)

d = ⁶ⁿ 2) ,

(n +1)( n + 3)

3 54

e = —---, (14)

(n + 2) ¹ ’

- 6 ln( a) w =-------,

ln(^ /2)

(15)

dan

₂ 1/2

a = ∑ "1 Xi- X ∣∕[ n ∑n=1( Xi— x) ] . (16)

IMPLEMENTASI UJI KENORMALN OMNIBUS

Berikut ini implementasi uji omnibus D’Agostino-Pearson K ² berdasarkan D’Agostino et al. (1990).

# fungsi DAP menghitung kepencongan,
# kurtosis
# dan statistik K^2

DAP.omnibus <- function(x,alpha){ n <- length(x) m2 <- sum((x - mean(x))^2)/n

m3 <- sum((x - mean(x))^3)/n

m4 <- sum((x - mean(x))^4)/n

# # prosedur pengujian kepencongan sqrt.b1 <- m3/(m2^1.5) cat("Kepencongan sampel:",sqrt.b1,"\n") a1 <- (n + 1)*(n + 3) a2 <- 6*(n - 2)

Y <- sqrt.b1*sqrt(a1/a2)

a3 <- 3*(n^2 + 27*n - 70)*(n + 1)*(n + 3)

a4 <- (n - 2)*(n + 5)*(n + 7)*(n + 9) betatwo.sqrt.b1 <- a3/a4

sqr.W <- -1 + sqrt(2*betatwo.sqrt.b1 -

1)

W <- sqrt(sqr.W)

delta <- 1/sqrt(log(W))

alpha <- sqrt(2/(sqr.W - 1))

Z.sqrt.b1 <- delta*log(Y/alpha + sqrt((Y/alpha)^2 + 1))

cat("Statistik uji

kepencongan:",Z.sqrt.b1,"\n")

# # prosedur pengujian kurtosis

b2 <- m4/(m2^2)

cat("Kurtosis sampel:",b2,"\n") a5 <- 3*(n - 1) a6 <- (n + 1)

E.b2 <- a5/a6

a7 <- 24*n*(n-2)*(n - 3)

a8 <- ((n + 1)^2)*(n + 3)*(n + 5) var.b2 <- a7/a8

x <- (b2 - E.b2)/(sqrt(var.b2)) a9 <- 6*(n^2 - 5*n + 2) a10 <- (n + 7)*(n + 9) a11 <- 6*(n + 3)*(n + 5) a12 <- n*(n - 2)*(n - 3) sqrt.betaone.b2 <-

(a9/a10)*sqrt(a11/a12)

a13 <- 8/sqrt.betaone.b2

a14 <- 2/sqrt.betaone.b2

a15	<- 1	+ (4/sqrt.betaone.b2)
A <-	6 +	a13*(a14 + sqrt(a15))
a16	<- 1	- (2/(9*A))
a17	<- 1	- 2/A
a18	<- 1	+ x*sqrt(2/(A - 4))
a19	<- s	qrt(2/(9*A))

Z.b2 <- (a16 - (a17/a18)^(1/3))/(a19) cat("Statistik uji

kurtosis:",Z.b2,"\n")

# # prosedur pengujian omnibus K^2 sqr.K <- (Z.sqrt.b1)^2 + (Z.b2)^2 cat("Statistik uji Agostino-Pearson K

kuadrat:",sqr.K,"\n")

if (sqr.K >= qchisq(1-alpha,2)) { cat("Hipotesis nol ditolak.","\n")

} else {

cat("Hipotesis nol tidak ditolak.", "\n")

}

Implementasi statistik uji modifikasi Jarque-Bera oleh Urzúa (1996).

# fungsi JBU omnibus mengimplementasikan
# modifikasi Jarque-Bera oleh Urzua

JBU.omnibus <- function(x,alpha){

n <- length(x)

m2 <- sum((x - mean(x))^2)/n

m3 <- sum((x - mean(x))^3)/n

m4 <- sum((x - mean(x))^4)/n sqrt.b1 <- m3/(m2^1.5) v1 <- 3*(n - 1)/(n + 1)

v2 <- 6*(n - 2)/((n + 1)*(n + 3))

v3 <- 24*n*(n - 2)*(n - 3)/

((n + 1)^2*(n + 3)*(n + 5))

b2 <- m4/(m2^2)

JBU <- (sqrt.b1)^2/(v2) + (b2-v1)/(v3) cat("Nilai statistik JBU:",JBU,"\n") if (JBU >= qchisq(1-alpha,2)) {

cat("Hipotesis nol ditolak.","\n")

} else {

cat("Hipotesis nol tidak ditolak.", "\n")

}

# Statistik Urzua (2007)

U.omnibus <- function(x,alpha){

n <- length(x)

m2 <- sum((x - mean(x))^2)/n

m3 <- sum((x - mean(x))^3)/n

m4 <- sum((x - mean(x))^4)/n sqrt.b1 <- m3/(m2^1.5)

d <- 6*(n-2)/((n + 1)*(n + 3))

e <- 3.54/(n + 2)

a <- sum(abs(x - mean(x)))/n*sum((x-mean(x)))

w <- -6*log(a)/log(pi/2)

U1 <- (sqrt.b1/d) + (w - 3)^2/e

U2 <- max(sqrt.b1/d,(w - 3)/sqrt(e)) cat("Nilai statistik U1:",U1,"\n") cat("Nilai statistik U2:",U2,"\n") if (U1 >= qchisq(1-alpha,2)) {

cat("Hipotesis nol ditolak.","\n")

} else {

cat("Hipotesis nol tidak ditolak.", "\n")

}

if (U2 >= 2.236) { %% alfa 5% cat("Hipotesis nol ditolak.","\n") } else {

cat("Hipotesis nol tidak ditolak.", "\n")

}

SIMPULAN

Implementasi uji omnibus di atas perlu disempuranakan lagi untuk menghitung p-value dan antisipasi terhadap data yang mengandung nol (0).

DAFTAR PUSTAKA

Bera, A. K. and Jarque, C. M. 1981. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals: Monte Carlo Evidence. Economics Letters. 7: 313—318.

Bonett, D. G. and Seier, E. 2002. A Test of Normality with High Uniform Power. Computational Statistics and Data Analysis. 40: 435—445.

Breton, M. D., Devore, M. D., and Brown, D. E. 2008. A Tool for Systematically Comparing the Power of Tests for Normality. Journal of Statistical Computation and Simulation. 78(7): 623—638.

Coin, D. and Corradetti, R. 2006 Tests for Normality: Comparison of Powers (Test di Normalità: Confronto delle Potenze). Alamat http://sis-statistica.it/files/pdf/atti/Spontanee2006_177-180.pdf accessed on 30 April 2010. 177—180.

D’Agostino, R. B., Belanger, A. and D’Agostino Jr., R. B. 1990. A Suggestion for Using Powerful and Informative Tests of Normality. The American Statistician. 44 (4): 316—321.

DeCarlo, L. T. 1997. On the Meaning and Use of Kurtosis. Psychological Methods. 2(3): 292—307.

Dufour, J-M., Farhat, A., Gardiol, L. and Khalaf, L. 1998. Simulation-based Finite Sample Normality Tests in Linear Regressions. Econometrics Journal. 1: 154—173.

Farrell, P. J. and Rogers-Stewart, K. 2006. Comprehensive Study of Tests for Normality and Symmetry: Extending the Spiegelhalter Test. Journal of Statistical Computation and Simulation. 76(9): 803—816.

Jarque, C. M. and Bera, A. K. 1980. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals. Economics Letters. 6. 255—259.

Jarque, C. M. and Bera, A. K. 1987. A Test for Normality of Observations and Regression Residuals. International Statistical Review. 55(2):163—172.

Koziol, J. A. 1986. Relative Efficiencies of Goodness of Fit Procedures for Assessing Univariate Normality. Annals of the Institute of Statistical Mathematics. 38(Part A): 485—493.

Seier, E. 2002. Comparison of Tests for Univariate Normality. InterStat.

Alamathttp://interstat.statjournals.net/YEAR/200 2/articles/0201001.pdf accessed on 30 April 2010.

Stephens, M. A. 1972. EDF Statistics for Goodness-of-Fit: Part I. Technical Report No. 186. Stanford University California.

Tanweer-ul-Islam. 2008. Normality Testing—A New Direction. Munich Personal RePEc Archive (MPRA) Paper No. 16452. Alamat

http://mpra.ub.uni-muenchen.de/16452 accessed on 30 April 2010.

Tanweer-ul-Islam and Zaman A. 2008. Normality Testing—A New Direction. Alamat http://www.economics.smu.edu.sg/femes/2008/C S_info/papers/418.pdf accessed on 30 April 2010.

Urzúa, C. M. 1996. On the Correct use of Omnibus Tests for Normality.Econometric Letters.53: 247—251.

Urzúa, C. M. 2007. Portable and Powerful Tests for Normality. Latin American Meeting of the Econometric Society. Universidad de los Andes. Bogotá. Colombia. Octubre. Internacional. Alamat http://www.webmeets.com/files/papers/LACEA-LAMES/2007/591/Portable.pdf accessed on 30 April 2010.

Yazici, B. and Yolacan, S. 2007. A Comparison of Various Tests of Normality. Journal of Statistical Computation and Simulation. 77(2): 175—183.

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d1	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
d2	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
d3	7	12	17	22	27	32	37	42	47	52	57	62	67	72	77
d4	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
k	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
d1	32	34	36	38	40	42	44	46	48	50	52	54	56	58	60
d2	48	51	54	57	60	63	66	69	72	75	78	81	84	87	90
d3	82	87	92	97	102	107	112	117	122	127	132	142	147	152	157
d4	67	71	75	79	83	87	91	95	99	103	107	111	115	119	123
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d1	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
d2	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
d3	7	12	17	22	27	32	37	42	47	52	57	62	67	72	77
d4	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
k	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
d1	32	34	36	38	40	42	44	46	48	50	52	54	56	58	60
d2	48	51	54	57	60	63	66	69	72	75	78	81	84	87	90
d3	82	87	92	97	102	107	112	117	122	127	132	142	147	152	157
d4	67	71	75	79	83	87	91	95	99	103	107	111	115	119	123
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155

BY MEANS OF LINDEBERG’S CENTRAL LIMIT THEOREM

CONSTRUCTION OF A h -GENERALIZED STANDARD BROWNIAN SHEET BY MEANS OF LINDEBERG’S CENTRAL LIMIT THEOREM

ABSTRACT

1. INTRODUCTION

k u )

P ^

[ns] [nt]

2. TIGHTNESS IN C(I)

3. MAIN RESULT

∖ (

4. SIMULATION

p {∖s,k∣ ≥ ■ }=p.

≤ 42

nλ

c1—α := 1

tα tα tα

P{K ≥ ~ J = α, P{KS ≥ ~1^} = α and

tα tα

5. CONCLUSION

REFERENCES

INTISARI

MAX-PLUS ALGEBRA MODELLING AND PERFORMANCE EVALUATION OF QUEUEING NONCYCLIC FORK-JOIN NETWORK WITH INFITE BUFFER CAPACITY

ABSTRACT

1. PENDAHULUAN

2. ALJABAR MAX-PLUS DAN TEORI GRAF

A* : = E ⊕ A ⊕ L ⊕ A ⊗ ⊕ A ⊗ ⊕ L dan

Bukti:

⊕ L ⊕ B⊗ .

Bukti:

Bukti:

Bukti:

= A⊗ ⊗ x ⊕ A ⊗ b ⊕ b

= A⊗ ⊗ x ⊕ (E ⊕ A) ⊗ b.

x = A⊗3⊗ x ⊕ (E ⊕ A ⊕A⊗2) ⊗ b.

3. MODEL JARINGAN ANTRIAN FORK-JOIN TAKSIKLIK

Bukti:

Contoh 1.

4. EVALUASI KINERJA JARINGAN ANTRIAN

Contoh 2:

Bukti:

DAFTAR PUSTAKA

BEBERAPA SIFAT IDEAL GELANGGANG POLINOM MIRING: SUATU KAJIAN PUSTAKA

INTISARI

SOME IDEAL PROPERTIES OFSKEW POLYNOMIAL RING: A LITERATURE STUDY

ABSTRACT

1. PENDAHULUAN

p = ∑ aixi, r∈Z+={0,1,l}, ai ∈ R, i= 1,l,r. i=0

2. MASALAH DAN PEMBAHASAN

2.1 Ideal dari Gelanggang Polinom Miring R [ x; σ, δ]

Bukti:

a (fj+ f1x + l + fnxn) = (fj+ f1x + l + fnxn) b.

Bukti:

Bukti:

2.2 Ideal σ- prim dari Gelanggang Polinom Miring R[x; σ , δ]

Bukti:

⇐

⇒

Bukti:

3. SIMPULAN

UCAPAN TERIMA KASIH

DAFTAR PUSTAKA

INTISARI

UNIVARIATE NORMALITY TEST: A LITERATURE STUDY

ABSTRACT

1. PENDAHULUAN

2.1 Uji Kenormalan Berdasarkan Fungsi Distribusi Empiris

G = n

U1 =

f

= max k

+ W f Mij

- 3

J

2.3. Uji Kenormalan Berdasarkan Korelasi atau Regresi

SW -

SF -

ci - Φ

U =

+

SYi = Ψ

^≤ 42

^c1—α ^:= 1

P{K ≥ ~ J = α, P{KS ≥ ~₁^} = α and

A^* : = E ⊕ A ⊕ L ⊕ A ^⊗ ⊕ A ^⊗ ⊕ L dan

⊕ L ⊕ B^⊗ .

= A^⊗ ⊗ x ⊕ A ⊗ b ⊕ b

= A^⊗ ⊗ x ⊕ (E ⊕ A) ⊗ b.

x = A^⊗³⊗ x ⊕ (E ⊕ A ⊕A^⊗²) ⊗ b.

SOME IDEAL PROPERTIES OF

SKEW POLYNOMIAL RING: A LITERATURE STUDY

p = ∑ aixⁱ, r∈Z₊={0,1,l}, ai ∈ R, i= 1,l,r. i=0

^a (^fj⁺^f1^x⁺^l⁺^fn^xn) = (^fj⁺^f1^x⁺^l⁺^fn^xn) b.

^-³

_-

MODEL PENYERAPAN OBAT UNTUK INTERVAL DAN DOSIS BERBEDA

I NYOMAN WIDANA

DRUG ABSORPTION MODEL FOR DIFFERENT INTERVALS AND DOSES

I NYOMAN WIDANA

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
d1	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
d2	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
d3	7	12	17	22	27	32	37	42	47	52	57	62	67	72	77
d4	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
d5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80
k	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
d1	32	34	36	38	40	42	44	46	48	50	52	54	56	58	60
d2	48	51	54	57	60	63	66	69	72	75	78	81	84	87	90
d3	82	87	92	97	102	107	112	117	122	127	132	142	147	152	157
d4	67	71	75	79	83	87	91	95	99	103	107	111	115	119	123
d5	85	90	95	100	105	110	115	120	125	130	135	140	145	150	155