Implementasi Metode Hybrid Particle Swarm Optimization dan Genetic Algorithm Pada Penjadwalan Job Shop Scheduling

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 11, No 3. February 2023

Implementasi Metode Hybrid Particle Swarm Optimization dan Genetic Algorithm Pada Penjadwalan Job Shop Scheduling

Anak Agung Putra Adnyana ¹, I Made Widiartha ², Agus Muliantara ³, Luh Gede Astuti ⁴, Made Agung Raharja ⁵, I Dewa Made Bayu Atmaja Darmawan ⁶

Program Studi Informatika Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana Jl. Raya Kampus Unud, Indonesia Bukit Jimbaran, Badung, Bali

Kode Pos: 80364 Indonesia

• ¹    [email protected], ² [email protected], ³ [email protected], ⁴ [email protected], ⁵ [email protected], ⁶ [email protected]

Abstract

Job shop problem is one of the non-deterministic combinatorial optimization problems with polynomial time (NP-complete). Genetic Algorithm optimization will be applied to solve Job Shop problems. hybrid particle swarm optimization. In this study.This Study is an attempt to solve Job Shop Scheduling problem using hybrid particle swarm optimization and genetic algorithm method, to find minimum Makespan. 5 parameters, C1, C2, inertia weight, crossover rate and mutation rate, will be compared with a range from 0.1 to 1 with difference 0.2, the test will look for combination parameter that get the minimum Makespan, The results of the implementation of the hybrid particle swarm optimization method and genetic algorithm are makespan of 29 days is obtained with an objective function value of 0.0043, with optimal parameters (C1) = 0.7, (C2) = 0.3, (w) = 0.3, (Cr) = 0.5, and (Mr) = 0.7.

Keywords: Job shop scheduling, Particle swarm optimization, Genetic algorithm, Makespan, Parameter

• 1.   Pendahuluan

Dalam dunia industri, proses produksi merupakan proses pembuatan barang atau jasa. Sebelum proses produksi dimulai atau konversi input menjadi produk perusahaan, perlu untuk mengembangkan jadwal produksi yang komprehensif. Diharapkan dengan dilakukannya penjadwalan produksi proses produksi dapat berjalan dengan lancar dan efisien [1]. Dengan waktu yang efisien tersebut diharapkan industri dapat mengurangi pengeluaran biaya produksi serta dapat memenuhi kebutuhaan konsumen tepat waktu, oleh karena itu pemahaman mengenai konsep penjadwalan sangat penting, sehingga para pekerja mengetahui kapan waktu harus memulai suatu pekerjaan dan kapan waktu mengakhirinya. Penjadwalan disusun dengan mempertimbangkan berbagai batasan yang ada. Penjadwalan yang baik akan memberikan dampak positif, yaitu rendahnya biaya operasi dan waktu pengiriman, yang akhirnya dapat meningkatkan kepuasan pelanggan.

Penjadwalan produksi merupakan bagian integral dari sistem perusahaan manufaktur. Permasalahan penjadwalan adalah menugaskan mesin produksi untuk melakukan serangkaian kegiatan melakukan pekerjaan dalam waktu tertentu sampai mencapai tujuan tertentu [2]. Konsep penjadwalan produksi merupakan salah satu contoh dari permasalahan dunia nyata dari Scheduling Problem (SP), SP adalah masalah yang berkaitan dengan pengurutan pemrosesan sejumlah pekerjaan pada sejumlah mesin. SP merupakan permasalahan yang memiliki karakteristik terdiri dari m mesin dan n pekerjaan. Setiap pekerjaan harus diproses pada setiap mesin. Masing-masing mesin dapat memroses paling banyak satu pekerjaan pada suatu waktu. Setiap pekerjaan harus diproses pada suatu mesin selarna suatu periode waktu tertentu tanpa interupsi. Setiap pekerjaan hanya dapat diproses oleh satu mesin dalam satu waktu. perusahaan manufaktur bekerja dengan berbagai sistem produksi, antara lain flow shop dan job shop. Sistem produksi job shop merupakan penjadwalan yg mempunyai hambatan urutan pemrosesan pekerjaan, dan setiap pekerjaan wajib melalui setiap mesin tepat satu kali. Penjadwalan job shop bisa dikelompokkan menurut waktu kedatangannya. job shop statis adalah jika seluruh pekerjaan diterima dalam waktu yg sama. Job shop dinamis yaitu jika ketika kedatangan pekerjaan diterima dalam waktu yg bervariasi. Job shop deterministik apabila variasi waktu kedatangannya diketahui sebelumnya. Tetapi apabila waktu kedatangan yang bervariasi tidak diketahui sebelumnya maka dianggap penjadwalan job shop non deterministik atau stokastik [3]. Dalam penelitian ini tujuan

Adnyana, Widiartha, Muliantara, Astuti, Raharja, Darmawan

Implementasi Metode Hybrid Particle Swarm Optimization dan Genetic Algorithm Pada Penjadwalan

Job Shop Scheduling yang akan dicapai adalah menghasilkan jadwal dengan makespan yang pendek,dimana makespan merupakan waktu penyelesaian paling akhir dari seluruh pekerjaan pada seluruh mesin [4].

Pada penelitian ini metode hybrid particle swarm optimization dan genetic algorithm digunakan untuk mencari solusi optimal dari masalah penjadwalan job shop. Tujuan dari penelitian ini adalah untuk meminimalkan total waktu produksi untuk menyelesaikan semua pekerjaan. Untuk mencapai rencana produksi yang optimal (biaya produksi minimal)

• 2.    Metodelogi Penelitian

  • 2.1   Job Shop Scheduling

Job Shop Scheduling Problem (JSSP) merupakan masalah penjadwalan yang banyak digunakan pada industri dengan tipikal pesanan adalah made to order, barang Pesanan akan diproduksi apabila hanya terdapat pesanan dari pelanggan. Penjadwalan JSSP adalah jenis penjadwalan yang rumit, salah satu penyebabnya adalah jenis produk atau variasi produk yang ditangani sangat bervariasi. Banyaknya variasi berdasarkan pesanan mengakibatkan timbul banyak jenis pekerjaan dan kebutuhan penggunaan alat yang berbeda. JSSP dapat dijelaskan sebagai berikut:

Terdapat n pekerjaan yang harus diselesaikan selama rentang waktu [T1, T2]. Pekerjaan ini akan diproses pada m mesin dengan prosedur pemesinan yang diberikan. Setiap pekerjaan dapat diproses pada satu dan hanya satu mesin pada satu waktu dan setiap mesin dapat memproses satu dan hanya satu pekerjaan pada satu waktu. Waktu pemrosesan setiap pekerjaan pada setiap mesin adalah tetap dan diasumsikan telah diketahui sebelumnya [5]. Adapun komponen-komponen pembentuk permasalah JSSP adalah sebagai berikut:

• 1.    Rentang waktu pengerjaan [T1, T2], biasanya dalam satuan hari, minggu, atau bulan. (T1 adalah waktu pekerjaan di terima, T2 adalah batas waktu pengerjaan)

• 2.    Pekerjaan J = {J₁,}₂,}₃, -,}_n}, n adalah jumlah dari seluruh pekerjaan.

• 3.    MesinM = {M₁,M₂,M₃, ...,M_m}, m adalah dari seluruh mesin.

• 4.    Matriks urutan pengerjaan SJM untuk setiap pekerjaan J, dapat digambarkan sebagai berikut:

_ Γ$11   $12 ..   S_itI

$^JM = ^[$21  $22.   $k\

Dimana Sik adalah urutan pengerjan dari job ke-i di mesin ke-k

• 5.    Matriks waktu pengerjaan TJM untuk setiap pekerjaan J, dapat digambarkabn sebagai berikut:

_τ       rT11    T12....    T_ikI

^l^    [T21   T₂₂....   Tiki

Dimana Tik adalah urutan pengerjan dari job ke-i di mesin ke-k

• 2.2    Metode Hybrid Particle Swarm Optimization dan Genetic Algorithm

Seperti Namanya metode yang diusulkan dalam penelitian ini menggabungkan dua buah algoritma yaitu Genetic Algorithm yang diusulkan oleh Golberg sebagai metode pencarian heuristic yang menyalin seleksi alam [6]. Dan Particle Swarm Optimization atau yang biasa disingkat PSO dimana merupakan salah satu metode heuristic yang biasa digunakan dalam optimasi. Particle Swarm Optimization terinspirasi oleh pola berkelompok (swarm) burung atau ikan [7]. Proses penerapan metode kedalam permasalahan secara tidak langsung di bagi menjadi dua tahap yaitu tahap GA dan juga Tahap PSO, yang nantinya akan di gabungkan menjadi metode hybrid. Berikut merupakan langkah langkahnya:

• 1.    Menginputkan data yang akan di proses dalam algoritma, yaitu:

• a.    Seq_machine adalah matriks urutan pengerjaan.

• b.    pcs_time adalah matriks waktu pengerjaan.

• 2.    Menginputkan parameter yang akan digunakan yaitu:

• a.    W adalah faktor inertia.

• b.  c₁ adalah koefisien percepatan partikel.

• c.  c₂ adalah koefisien percepatan populasi.

• d.  Penum adalah ukuran populasi.

• e.  rmax adalah penghitung iterasi maks.

• f.   Pc adalah probabilitas crossover partikel.

• g.  Pm adalah probabilitas mutasi.

• h.  V_j adalah kecepatan partikel

• i.   X_tJ(t) adalah Partikel saat ini

• j.    R₁ & R₂ adalah bilangan random (0-1)

• 3.    Inisialisasi populasi partikel dengan posisi dan kecepatan acak pada dimensi-D, setiap partikel mewakili posisi kandidat pekerjaan. Sebuah partikel dianggap sebagai titik dalam ruang dimensi-D.

• 4.    Hitung nilai fungsi objektif untuk setiap partikel populasi pada iterasi r.

• 5.    Perulangan iterasi terjadi selama r < rmax dan nilai selisih Gbest [r] – Gbest [r -1] < 0.00001, selisih terjadi lebih dari 20 kali, jika tidak terpenuhi, hentikan algoritma dan Gbest terakhir menjadi solusi optimal.

• 6.    Elitism. Masukan partikel dari populasi dengan nilai fitness terbaik ke generasi berikutnya.

• 7.    Operasi Crossover. Dua partikel dalam populasi dipilih dengan probabilitas Pc sebagai partikel induk untuk operasi crossover. Silangkan induk dengan partikel dalam populasi.

• 8.    Operasi Mutation. Hasilkan partikel baru dengan menukar gen dari partikel terbaik. Operator ini dapat secara signifikan meningkatkan keragaman populasi dan menghindari masalah lokal optima.

• 9.    Operasi Repair. Operator ini digunakan untuk memeriksa kelayakan partikel di populasi. Operator Repair digunakan untuk memperbaiki gen yang tidak layak dari partikel menjadi layak. Ide tentang operator ini adalah untuk memisahkan gen yang layak dalam suatu partikel dari yang tidak layak, dan mengembangkan bersama gen yang tidak layak sampai mereka menjadi layak. Cara spesifik untuk melakukan langkah ini adalah menemukan gen yang hilang dari gen partikel, dan kemudian menempelkan gen yang hilang di akhir gen yang baru dihasilkan.

• 10.    Update nilai fittnes dari setiap partikel. Pbest adalah nilai terbaik untuk partikel i selama proses iterasi, dan P_r¹ Adalah fitness partikel i saat ini. Jika P_r^l < Pbest ditetapkan, lalu set Pbest = P_r¹, jika tidak, Pbest tetap.

• 11.    Update nilai fittnes dari populasi. Petakan posisi setiap partikel ke dalam ruang solusi dan mengevaluasi nilai kesesuaiannya sesuai dengan fungsi objektif. Tentukan Gbest sebagai nilai terbaik dari populasi partikel, Gbest = min (Pbest), (nilai i = 1, ..., Penum).

• 12.    Update kecepatan dan posisi, hal tersebut diperbarui sesuai dengan persamaan (1) dan persamaan (2). Kembali ke Langkah 3 setelah memperbarui kecepatan dan posisi dan memulai iterasi baru.

V_ij(t+1) = W × V_ij(t) + c₁×R₁× (Pbest- X_ij(t)) + c₂×R₂× (Gbest- X_ij(t))         (1)

^x_j(t ⁺ 1) = ^xij(t) ^{+ V}ij^(t + 1)                                                                 (2)

• 2.3    Data

Data yang digunakan untuk penelitian ini adalah data mesin, data order/pekerjaan, data urutan pengerjaan, data waktu pengerjaan. Jenis data yang dipakai pada penelitian ini merupakan data sekunder. Data sekunder yang di gunakan dalam penelitian kali ini bersumber dari penelitian Purwaningsih dan Fitriana (2016) [8]. Jumlah keseluruhan data yang digunakan terdiri dari 27 buah pesanan barang yang berbentuk furniture.

• 3.    Hasil dan pengujian

Fungsi objektif merupakan tujuan dari penjadwalan yang dilakukan. Dalam permasalahan penelitian ini fungsi objektif merupakan meminimasi makespan.

makespan = PT_x(mS) +  PT_x(mS)+_n                                                 (3)

Lantaran tujuan penjadwalan merupakan meminimalkan sedangkan prinsip algoritma genetika merupakan memaksimasia, maka nilai fungsi fitness dalam masalah ini menjadi:

F(X) = —¹--- (4)

makespan

• 3.1.    Pengujian

Pada penelitian ini akan dilakukan pengujian menentukan solusi optimal dengan beberapa parameter antara lain koefisien percepatan partikel (C1), koefisien percepatan populasi (C2), Inertia weight (w), probabilitas crossover, probabilitas mutation. Data akan diuji parameternya untuk melihat pengaruh nilai parameter terhadap makespan atau waktu pengerjaan dari jadwal yang dihasilkan. Keseluruhan Parameter yang akan diuji memiliki rentang uji dari 0.1 sampai 1 dengan selisih 0,2, dan dengan nilai parameter tetap seperti jumlah populasi sama dengan 100 jumlah iterasi sama dengan 1000.

• 3.2.    Hasil Penelitian

Berikut merupakan hasil terbaik dari pengujian parameter yang direncanakan sebelumnya, nantinya hasil ini akan dibandingkan dengan hasil dari penelitian sebelumnya [8].

Koefisien kecepatan (C1)

Keofisien kecepatan (C2)

0.0044

0.0043

!o' 0.0042

O 0.0041

S) 0.004

§ 0.0039

0.0038

= 0.0037

0.0044 0.0043

!o' 0.0042

O 0.0041

S) 0.004 § 0.0039 0.0038 = 0.0037

0.1    0.3    0.5    0.7    0.9

0.1    0.3    0.5    0.7    0.9

Axis Title

Axis Title

—•—Koefisien kecepatan (C1)

—•— Keofisien kecepatan (C2)

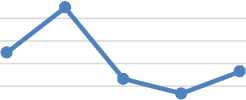
Gambar 1. Hasil pengujian parameter koefisien Gambar 2. Hasil pengujian parameter koefisien kecepatan (C1) PSO-GA kecepatan (C2) PSO-GA

Pada Gambar 1 menunjukan perubahan dari parameter koefisien C1 dimana fungsi objektif memiliki puncak/ nilai terbaik pada nilai 0.7 yang mana pada nilai parameter sebelumnya memiliki nilai fungsi objektif yang hampir sama, ini menyebabkan nilai 0.7 menjadi nilai parameter optimal untuk koefisien percepatan C1. Sedangkan pada gambar 2 menunjukan perubahan dari parameter koefisien C2 dimana fungsi objektif memiliki puncak/ nilai terbaik pada nilai 0.3 dan nilai setelahnya mengalami penurunan, ini menyebabkan nilai 0.3 menjadi nilai parameter optimal untuk koefisien percepatan C2.

Inertia Weight (w)

0.0044

0.0043

S' 0.0042

S 0.0041

0.004

0.0039

= 0.0038

Crossover Rate

0.0044

0.0043

S' 0.0042

S 0.0041 ⊂?  0.004

0.0039 = 0.0038

0.1    0.3    0.5    0.7    0.9

0.1    0.3    0.5    0.7    0.9

Axis Title

Axis Title

—•—Inertia Weight (w)

—•— Crossover Rate

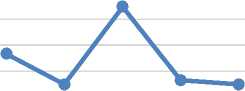
Gambar 3. Hasil pengujian parameter inertia Gambar 4. Hasil pengujian parameter ^weight (^w) ^PSO-GA crossover rate (Cr) PSO-GA

Pada Gambar 3 menunjukan perubahan dari parameter inertia weight (w) dimana fungsi objektif memiliki puncak/ nilai terbaik pada nilai 0.3 yang mana pada nilai parameter selanjutnya mengalami penurunan lalu mendatar, ini menyebabkan nilai 0.3 menjadi nilai parameter optimal untuk inertia weight (w). Pada Gambar 4 menunjukan perubahan dari parameter crossover rate (Cr) dimana fungsi objektif memiliki puncak/ nilai terbaik pada nilai 0.5 dimana nilai sebelumnya mengalami penurunan dan setelahnya mendatar, ini menyebabkan nilai 0.5 menjadi nilai parameter optimal untuk crossover rate (Cr).

Mutation Rate

0.0044

0.0043

OJ

0.0042

O

0.0041

0.004

Z3

0.0039

0.0038

0.1    0.3    0.5    0.7    0.9

Axis Title

Mutation Rate

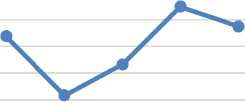
Gambar 5. Hasil pengujian parameter mutation rate (Mr) PSO-GA

Pada Gambar 5 menunjukan perubahan dari parameter mutation rate (Mr) dimana fungsi objektif memiliki puncak/ nilai terbaik pada nilai 0.7 dimana nilai sebelumnya mengalami penurunan lalu perlahan naik ke titik optimal dan setelahnya nilai menurun, ini menyebabkan nilai 0.7 menjadi nilai parameter optimal untuk mutation rate (Mr).

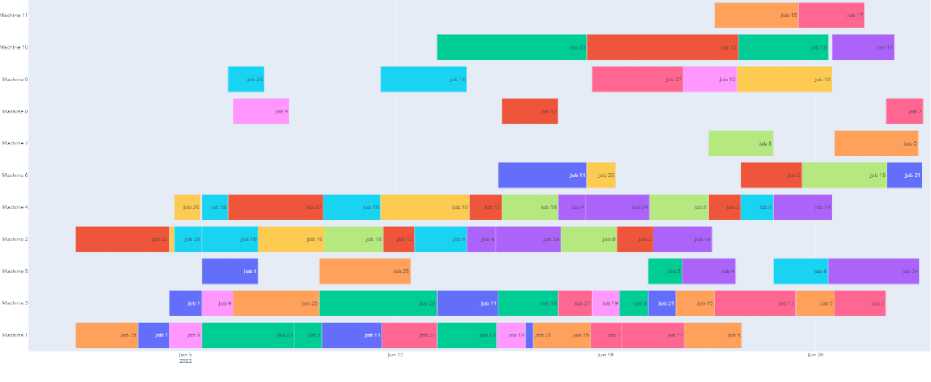
Gambar 6. Gant chart solusi optimal

Dapat dilihat seperti gambar 6 setiap warna dalam jadwal merepresentasikan sebuah pekerjaan yang dikerjakan, dan setiap baris merepresentasikan mesin yang berbeda. Panjang dari setiap bar merepresentasikan waktu dari pengerjaan sebuah pekerjaan, dan dari pengujian sebelumnya didapatkan hasil nilai fungsi objektif optimal sebesar 3.7 × 10^-3, dan gantt chart dari jadwal yang di generate dengan parameter optimal dapat dilihat di gambar 6, makespan dari hasil yang didapat adalah sebesar 29 hari.

Perbandingan metode hybrid particle swarm optimization dan genetic algorithm, Software WinQSB, dan penjadwalan manual

60

29

48

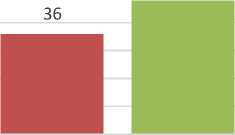
Makespan

PSO-GA WinQSB Manual

50

40

30

20

10

0

Gambar 7. Hasil Perbandingan metode hybrid, Software WinQSB, dan penjadwalan manual

Perbandingan hasil dari metode hybrid dengan penelitian sebelumnya dapat dilihat pada grafik yang terdapat pada gambar 7, jika dibandingkan dengan hasil dari penelitian sebelumnya [8] metode metode hybrid particle swarm optimization dan genetic algorithm mampu mengungguli dari hasil software WinQSB dan penjadwalan manual pada penelitian sebelumnya. Dari perbandingan tersebut dapat dikatakan metode hybrid particle swarm optimization dan genetic algorithm dapat menyelesaikan permasalahan Job shop scheduling dengan baik.

• 4.    Kesimpulan

Penelitian ini sudah berhasil mengimplementasikan metode hybrid particle swarm optimization dan genetic algorithm untuk mendapatkan jadwal pekerjaan optimal. adapun nilai parameter yang optimal untuk mendapatkan nilai fungsi objektif terbaik adalah parameter (C1) = 0.7, (C2) = 0.3, (w) = 0.3, (Cr) = 0.5, dan (Mr) = 0.7, dan variabel tetap jumlah populasi = 100, jumlah generasi = 1000 yang memiliki nilai fungsi objektif 0.0043, waktu pengerjaan atau makespan 29 hari dan biaya operasional sebesar Rp 21.085.198.

References

• [1]    I. Raharja, “Analisa Penjadwalan Proyek Dengan Metode Pert Di PT. Hasana Damai Putra

YOGYAKARTA Pada Proyek Perumahan Tirta Sani,” Bentang, vol. 2, no. 1, 2014.

• [2]    Y. Muharni dan D. A. Utami, “Menggunakan Metode Nawaz Enscore Ham Dan Genetic

Algorithm,” vol. V, no. 2, hal. 29–39, 2019.

• [3]    M. Saidah, Nafiuna Hidayatus, “Implementasi algoritma optimasi bee colony untuk

penjadwalan job shop,” J. Tek. ITS Vol. 1, no. October 2016, 2013.

• [4]    N. Azmi, I. Jamaran, Y. Arkeman, dan D. Mangunwidjaja, “Penjadwalan Pesanan

Menggunakan Algoritma Genetika untuk Tipe Produksi Hybrid and Flexible Flowshop pada Industri Kemasan Karton,” J. Tek. Ind., hal. 176–188.

• [5]    L. L. Liu, R. S. Hu, X. P. Hu, G. P. Zhao, dan S. Wang, “A hybrid PSO-GA algorithm for job

shop scheduling in machine tool production,” Int. J. Prod. Res., vol. 53, no. 19, hal. 5755– 5781, 2015, doi: 10.1080/00207543.2014.994714.

• [6]     M. O. Okwu dan L. K. Tartibu, “Genetic Algorithm,” Stud. Comput. Intell., vol. 927, hal. 125–

• 132,    2021, doi: 10.1007/978-3-030-61111-8_13.

• [7]    T. Mahardhika, “Hybrid Algorithm as alternative method for optimization, a combination

Genetic Algorithm and Particle Swarm Optimization,” J. Phys. Conf. Ser., vol. 1764, no. 1, 2021, doi: 10.1088/1742-6596/1764/1/012040.

• [8]    R. Purwaningsih dan I. C. Fitriana, “Analisis Penjadwalan Produk PT Eksotika Logam Bali (

DECO BALI ) dengan Minimasi Makespan,” hal. 124–131, 2016.

544