Fuzzy Inference System as a Method of Determining Drug Demand in Pharmacy Systems
on
p-ISSN: 2301-5373
e-ISSN: 2654-5101
Jurnal Elektronik Ilmu Komputer Udayana
Volume 11, No 3. February 2023
Fuzzy Inference System as a Method of Determining Drug Demand in Pharmacy Systems
Ni Made Rai Nirmala Santhia1, Ida Bagus Made Mahendra a2, Ngurah Agus Sanjaya ER a3, I Putu Gede Hendra Suputra a4, I Komang Ari Mogi a5, Agus Muliantaraa6
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana Badung, Bali, Indonesia
Abstract
In providing health services, puskesmas cannot be separated from the need for pharmaceutical preparations. Given the large influence of pharmaceutical preparations on the smoothness and performance of services at the puskesmas, it is necessary to pay special attention to managing them. However, prediction of demand is often difficult for officers, because it cannot be done by just anyone. Therefore, this study was conducted to provide consideration for the demand for pharmaceutical preparations in order to minimize the lack of pharmaceutical preparations. In the process, a demand analysis is carried out based on the number of uses and remaining inventory from the previous time period, to produce a prediction of the number of requests for pharmaceutical preparations. The method that will be used in this research is the Mamdani model fuzzy inference system, with interval determination based on the quartile method and the decile method. Which results obtained that the evaluation of predictive competence using both methods is sufficient. Namely, the Mean Absolute Percentage Error (MAPE) of the two methods is 26.43% for the decile method and 28.77% for the quartile method.
Keywords: Fuzzy Inference System, Prediction, Demand, Pharmaceutical inventory, Mamdani Method
Pusat kesehatan masyarakat yang seterusnya disebut puskesmas merupakan pelaksana fasilitas pelayanan dasar dalam upaya mewujudkan derajat kesehatan yang optimal bagi masyarakat [1]. Dalam memberikan pelayanan kesehatan, puskesmas tidak terlepas dari komidi utamanya yakni sediaan farmasi yang berupa obat, bahan obat, maupun kosmetika. Mengingat besarnya pengaruh sediaan farmasi untuk kelancaran pelayanan di puskesmas, maka perlu adanya perhatian khusus untuk mengelolanya. Pengelolaan sediaan farmasi, sangat penting dilakukan untuk menjaga ketersediaannya dalam membantu peningkatan kualitas pelayanan fasilitas kesehatan kepada masyarakat [2].
Kegiatan pengelolaan sediaan farmasi berupa perencanaan memiliki peran penting untuk menjaga persediaan farmasi. Perencanaan tersebut meliputi proses peramalan jumlah permintaan yang diperlukan dalam pemenuhan persediaan puskesmas. Prediksi jumlah permintaan sering menjadi kesulitan bagi petugas akibat tidak dapat dilakukan oleh sembarang orang karena perlunya pengalaman yang cukup lama untuk memberikan peramalan yang tepat agar tidak terjadinya kekurangan persediaan. Persediaan dilakukan untuk menjamin adanya kepastian bahwa pada saat dibutuhkan produk-produk tersebut tersedia. Untuk itu perlu adanya perencanaan persediaan yang berdasar dalam menyikapi pola permintaan yang pada dasarnya tidak beraturan [3].
Maka dari itu, untuk memberikan pertimbangan permintaan sediaan farmasi guna meminimalisir kurangnya, diperlukan analisis permintaan yang berdasar pada banyaknya penggunaan dan sisa persediaan dari periode waktu sebelumnya[4]. Dari data tersebut kemudian menghasilkan prediksi jumlah permintaan sediaan farmasi. Adapun metode yang akan digunakan dalam penelitian ini yaitu fuzzy inference system model mamdani, dengan penentuan interval dari himpunan fuzzy menggunakan metode kuartil maupun metode desil. Dengan dilakukannya prediksi permintaan sediaan farmasi menggunakan metode fuzzy inference system model mamdani, diharapkan dapat dijadikan bahan pertimbangan yang berdasar guna memberikan perancanaan yang baik dalam pengelolaan sediaan farmasi.
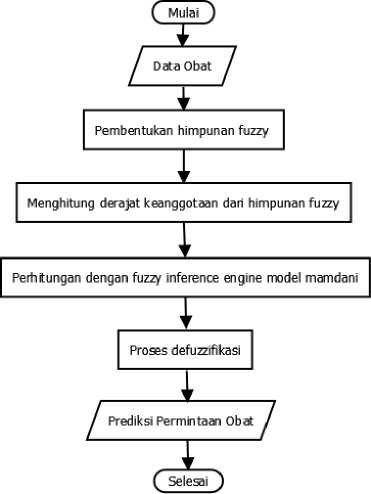
Terdapat beberapa tahapan dalam penerapan fuzzy inference sistem model mamdani, yaitu dengan alur sebagaimana pada gambar 1.
-
Gambar 1. Alur Umum Penelitian
Sebelum dilakukannya proses penerapan fuzzy inference system, terlebih dahulu dilakukan proses mempersiapkan data. Adapun proses mempersiapkan data meliputi pengambilan data, pembersihan data yang sesuai, serta melakukan proses input ke dalam system. Kemudian baru dapat dilakukan pengiolahan data sebagaimana alur penerapan fuzzy inference system. Adapun alur tersebut lebih jelasnya seperti berikut.
-
1. Pembentukan himpunan fuzzy menggunakan metode kuartile dan metode desil.
-
2. Menghitung fungsi keanggotaan dari himpunan fuzzy. Adapun fungsi keanggotaan yang
digunakan yaitu triangular membership function.
-
3. Perhitungan dengan fuzzy inference engine model mamdani.
-
4. Proses konversi hasil dari inference engine yang diekspresikan dalam bentuk fuzzy set ke suatu bilangan riil, proses ini disebut juga proses defuzzifikasi.
Pembentukan himpunan fuzzy yakni menentukan semua variabel yang terkait seperti jumlah sisa persediaan dan penggunaan sebagai fungsi input, yang menghasilkan permintaan sediaan farmasi sebagai fungsi output[5]. Adapun dalam penelitian ini dalam menentukan interval setiap himpunan menggunakan metode kuartil dan metode desil, dengan hasil sepert pada tabel 1.
Tabel 1. Interval dari Himpunan Fuzzy
|
Nama Variabel |
Semesta Pembicara |
Himpunan Fuzzy |
Interval Metode Kuartil |
Interval Metode Desil | |||
|
Jumlah Sisa Persediaan |
[0 |
Xs] |
Sedikit Sedang |
[0 [Q1 |
Q2] Q3] |
[0 [D1 |
D5] D9] |
|
Banyak |
[Q2 |
Xs] |
[ D5 |
Xs] | |||
|
Sedikit |
[0 |
Q2] |
[0 |
D5] | |||
|
Penggunaan |
[0 |
Xp] |
Sedang Banyak |
[Q1 [Q2 |
Q3] Xp] |
[ D1 [ D5 |
D9] Xp] |
|
Sedikit |
[0 |
Q2] |
[0 |
D5] | |||
|
Jumlah Permintaan |
[0 |
Xr] |
Sedang |
[Q1 |
Q3] |
[ D1 |
D9] |
|
Banyak |
[Q2 |
Xr] |
[ D5 |
Xr] | |||
Keterangan :
Xs : Nilai terbesar sisa persediaan.
Xp : Nilai terbesar sisa penggunaan.
Xr : Nilai terbesar sisa permintaan.
Dn : Desil ke-n dari variabel.
Qn : Kuartil ke-n dari variabel.
Fungsi keanggotaan divisualisasikan sebagai kurva yang memetakan nilai derajat dari keanggotaan input yang diberikan. Derajat keanggotaan tersebut merupakan representasi dari titik input dengan nilai keanggotaannya. Adapun interval nilai derajat keanggotaan suatu input antara 0 sampai dengan 1[5]. Adapun fungsi keanggotaan yang digunakan pada penelitian ini yaitu linear-triangular membership function, dengan batas bawah dari membership function ini yang akan ditentukan menggunakan metode kuartil dan metode desil. Yang selanjutnya masing – masing hasil perhitungan membership function akan melalui tahap selanjutnya untuk menghasilkan hasil prediksi dari kedua metode tersebut. Adapun contoh visualisasi membership function seperti berikut.
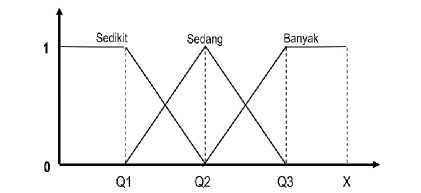
Gambar 2. Visualisasi Membership Function
Dari visualisasi tersebut, maka untuk perhitungan derajat keanggotaan seperti persamaan berikut.
|
μ Sedikit = { |
1 Q2 - Xi Q2 — Qi 0 |
; Xi ≤ Qi ; Qi ≤ Xi≤Q2 |
(1) | |
|
; Xi |
■ ≥ Q2 | |||
|
μSedang = |
0 Xj - Qi Q2 - Qi |
; Xi ≤ ; Qi ≤ χ |
Q1 atau xi ≥ Q3 i ≤ Q2 |
(2) |
|
μBanyak = { |
Q2--Ji- Q3 - Q2 0 Xj - Q2 Q3 - Q2 |
; Q2 ≤Xi ; Xi ; Q2 |
≤ Q3 ≤ Q2 ≤ Xi ≤Q3 |
(3) |
|
1 |
; Xi |
≥ Q3 | ||
-
2.3 Fuzzy Inference Engine Model Mamdani
Fuzzy inference engine Model Mamdani atau sering disebut juga dengan metode min-max. Pada tahap ini diawali dengan menetapkan aturan dengan betuk fungsi implikasi. Adapun aturan tersebut yaitu sabagaimana tabel 2. Setelah ditetapkan aturan implikasi, kemudian dilakukan proses implementasi fungsi implikasi dengan menggunakan min function atau disebut juga fungsi minimum berdasarkan aturan implikasi yang telah dibuat, untuk mendapatkan α-predikat setiap aturan[6]. Adapun fungsi minimum diekspresikan sebagai persamaan berikut.
Ham = min (Ha(S) ,μβ(P)) (4)
Keterangan:
Hang : Nilai hasil operator AND derajat keanggotaan atau a-precikat aturan ke-i.
Ha(S) : Derajat keanggotaan dari variabel sisa persediaan.
μg(P) : Derajat keanggotaan dari variabel pemakaian.
Selanjutnya yaitu mencari solusi fuzzy set dengan proses menghitung nilai maksimum tiap daerah himpunan fuzzy. Yang mana proses ini direpresentasikan dengan persamaan berikut.
μ(xi) = max ( μaf(xi) , μbf(xi), μcf (xi) ) (5)
Keterangan:
μ(xl) : Solusi fuzzy set himpunan fuzzy ke-i.
-
μaf(xt) : a-precukat aturan ke-a anggota himpunan fuzzy ke-i.
-
μbf(xi) : a-prectkat aturan ke-b anggota himpunan fuzzy ke-i.
-
μcf(xi) : a-vrecikat aturan ke-c anggota himpunan fuzzy ke-i.
Tabel 2. Fungsi Implikasi
|
Jumlah Sisa Persediaan |
Jumlah Penggunaan |
Jumlah Permintaan |
|
Sedikit |
Sedikit | |
|
Sedikit |
Sedang |
Sedang |
|
Banyak |
Banyak | |
|
Sedikit |
Sedikit | |
|
Sedang |
Sedang |
Sedang |
|
Banyak |
Sedang | |
|
Sedikit |
Sedikit | |
|
Banyak |
Sedang |
Sedikit |
|
Banyak |
Sedang |
Defuzzifikasi merupakan proses mengkonversi setiap hasil dari inference engine yang diekspresikan dalam bentuk fuzzy set ke suatu bilangan real. Adapun disini menggunakan metode centroid atau disebut juga center of area (center of gravity) yang mana mencari hasil prediksi dengan melakukan perhitungan untuk mencari titik pusat daerah fuzzy[5]. Dalam menghitung titik tengah dilakukan dengan mengitung nilai moments dan luas setiap daerah.
Mi = ∫aμ zi d( Zi) (6)
Ai = (a - b) × μ (7)
Ai
(a - b) × (na + μb) 2
(8)
Z =
∑K iMl
∑
n
Al
(9)
Keterangan:
Mi : Moment daerah ke-i.
Ai Zi a
d( Zi)
: Luas daerah ke-i.
: Diintegralkan terhadap nilai daerah ke-i.
: Batas atas/akhir (daerah solusi).
b : Batas bawah/awal (daerah solusi).
Z : Nilai titik tengah (output)
-
2.5 Mean Absolute Percentage Error (MAPE)
Mean Absolute Percentage Error (MAPE) merupakan nilai rata – rata perbedaan absolut diantara nilai prediksi dan nilai realisasi yang dikalikan dengan seratus persen[7]. MAPE disebut juga sebagai hasil persenan dari nilai realisasi. Penggunaan MAPE yaitu untuk evaluasi hasil peramalan berupa tingkat akurasi angka peramalan terhadap angka realisasi[8]. Dengan kemudian hasil perhitungan MAPE kemudian dievaluasi berdasarkan pada tabel 3.
MAPE = ⅛-1 |^^| × 100%
(10)
n t=1 Qt
keterangan:
|
Qt |
: nilai actual |
|
Pt |
: nilai prediksi |
|
n |
: jumlah data |
Tabel 3. Indikator evaluasi
|
MAPE Range |
Keterangan |
|
< 10% 10% - 20% 21% - 50% >50% |
Kompetensi model prediksi sangat baik. Kompetensi Model Prediksi Baik. Kompetensi model prediksi cukup. Kompetensi model prediksi buruk. |
Adapun implementasi prediksi menggunakan fuzzy inference system model mamdani ke dalam visualisasi website dapat dilihat seperti pada gambar berikut.
Gambar 3. Halaman Login
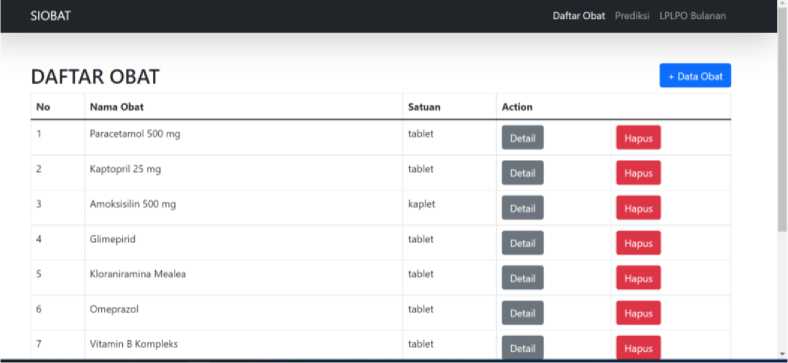
Gambar 4. Halaman Daftar Obat
Gambar 5. Halaman Tambah Data Obat
Gambar 6. Halaman Detail Obat
Adapun website akan digunakan oleh petugas kefarmasian. Dengan petugas terlebih dahulu login menggunakan username dan password pada kolom yang disediakan, seperti pada gambar 3 alaman login website. Selanjutnya petugas akan diarahkan pada tampilan daftar obat seperti pada gambar 4.
Petugas dapat melakukan penambahan data dengan tombol tambah data obat melakukan update data serta melihat prediksi dengan tombol detail, dan menghapus data dengan tombol hapus. Adapun tampilan untuk menambah obat seperti pada gambar 5. Pada gambar 6 menampilkan detail dari suatu obat, dengan detail tampilan terdapat input data dan menampilkan hasil prediksi. Petugas terlebih dahulu melakukan input tahun dan bulan dari satu obat. Kemudian dilakukan proses input dari pemakaian dan sisa stok, yang selanjutnya menghasilkan nilai prediksi permintaan obat. Selanjutnya petugas dapat memasukan nilai dari permintaan yang sebenarnya. Jika data sebelumnya sudah ada, maka akan menampilkan data sebelumnya yang telah tersimpan.
Pada penelitian ini dilakukan menggunakan data sisa persediaan dan penggunaan obat untuk menentukan jumlah permintaan obat yang dibutuhkan untuk memenuhi kebutuhan bulan selanjutnya. Adapun prediksi permintaan obat dilakukan menggunakan fuzzy inference system model mamdani, dengan penentuan interval himpunan fuzzy dilakukan dengan metode kuartil serta metode desil. Berikut pada tabel 3 merupakan contoh dari penentuan himpunan fuzzy.
|
Tabel 4. Penentuan Himpunan Fuzzy | |
|
Variable |
Semesta Interval Metode Interval Pembicara Himpunan Fuzzy Kuartil Metode Desil |
|
Jumlah Sisa Persediaan |
Sedikit [0 652] [0 652] [0 1304] Sedang [326 978] [131 1174] Banyak [652 1304] [652 1304] |
|
Jumlah Penggunaan |
Sedikit [0 1188] [0 1188] [0 2375] Sedang [594 1782] [238 2138] Banyak [1188 2375] [1188 2375] |
|
Jumlah Permintaan |
Sedikit [0 1500] [0 1500] [0 3000] Sedang [750 2250] [300 2700] Banyak [1500 3000] [1500 3000] |
Setelah ditentukannya interval dari setiap himpunan, selanjutnya dilakukan proses menghitung derajat keanggotaan. Adapun nilai dari derajat keanggotaan berkisar antara 0 hingga 1. Pada tabel 4 berikut merupakan contoh menghitung derajat keanggotaan dari variabel jumlah sisa persediaan dengan interval menggunakan metode kuartil.
Tabel 5. Menghitung Derajat Keanggotaan
|
Himpunan Fuzzy |
Interval |
Perhitungan |
Pemenuhan Kondisi |
Derajat Keanggotaan |
|
(phi) S sedikit |
x1 <= 326 |
1 |
no |
0,9447 |
|
326 <= x1 <= 652 |
(652 - x1) : 326 |
yes | ||
|
x1 >= 652 |
0 |
no | ||
|
(phi) S sedang |
x1 <= 326 or X1 >= 978 |
0 |
no | |
|
326 <= x1 <= 652 |
(X1 - 326) : 326 |
yes |
0,0552 | |
|
652 <= x1 <= 978 |
(978 - x1) : 326 |
no | ||
|
(phi) S banyak |
x<=652 652 <= x1 <= 978 x1 >=978 |
0 (X1 - 652) : 326 1 |
yes no no |
0 |
Selanjutnya dilakukan proses implementasi fungsi implikasi, dengan penerapan fungsi minimum dan maksimum. Pada tabel 5 merupakan contoh penerapan fungsi minimum, dan dilanjutkan dengan penerapan fungsi maksimum dengan hasil seperti tabel 6. Adapun hasil tersebut berdasar dari hasil
perhitungan derajat keanggotaan sebelumnya, yang kemudian menghasilkan daerah penyelesaian fuzzy. Adapun visualisasi daerah penyelesaian fuzzy untuk variabel jumlah sisa persediaan seperti pada gambar 7.
Tabel 6. Penerapan Fungsi Minimum
|
Jumlah Sisa Persediaan |
Jumlah Penggunaan |
Jumlah Permintaan |
Himpunan Fungsi Rule |
|
0,9447 |
0 |
0 |
Sedikit |
|
0,9447 |
0 |
0 |
Sedang |
|
0,9447 |
1 |
0,9447 |
Banyak |
|
0,0552 |
0 |
0 |
Sedikit |
|
0,0552 |
0 |
0 |
Sedang |
|
0,0552 |
1 |
0,0552 |
Banyak |
|
0 |
0 |
0 |
Sedikit |
|
0 |
0 |
0 |
Sedang |
|
0 |
1 |
0 |
Banyak |
Tabel 7. Penerapan Fungsi Maksimum
|
Himpunan Fuzzy |
Alpha Predicate |
|
Sedikit |
0 |
|
Sedang |
0 |
|
Banyak |
0,9447 |
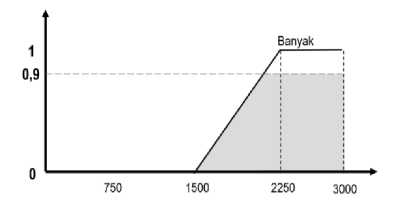
Gambar 7. Visualisasi Daerah Penyelesaian Fuzzy
Setelah dilakukan perhitungan dari setiap variabel sehingga menghasilkan daerah penyelesaian fuzzy, kemudian dilakukan proses defuzzifikasi untuk mengubah bentuk fuzzy set ke suatu bilangan riil. Adapun proses defuzzifikasi diawali dengan menghitung momen dan luas daerah penyelesaian fuzzy seperti pada persamaan (6), (7), dan (8). Lalu dilakukan proses menghitung titik tengah sebagaimana persamaan (9). Berikut merupakan contoh hasil prediksi permintaan obat.
|
Tabel 8. Penerapan Fungsi Maksimum | |||||
|
Nama Obat |
Sisa Persediaan |
Pemakaian |
Prediksi Kuartil |
Prediksi Desil |
Permintaan Sebenarnya |
|
Amoksisilin kaplet 500 mg |
631 |
1990 |
2431 |
2193 |
1500 |
|
Glimepirid tablet 1mg |
837 |
1747 |
1559 |
1363 |
1000 |
|
Kaptopril tablet 25 mg |
416 |
3140 |
3665 |
3191 |
3000 |
|
Ctm tablet 4 mg |
147 |
1279 |
1612 |
1673 |
1500 |
|
Omeprazol |
0 |
600 |
385 |
308 |
300 |
|
Parasetamol tablet 500mg |
313 |
3865 |
2981 |
3180 |
3700 |
|
Vitamin b kompleks tablet |
683 |
5794 |
6318 |
5015 |
5500 |
Dari hasil prediksi permintaan obat menggunakan fuzzy inference system dengan penentuan interval dengan metode kuartil dan desil, dilakukan evaluasi berdasarkan pada mean absolute percentage error sebagaimana persamaan (10) menghasilkan hasil prediksi seperti pada tabel 8. Berdasarkan
hasil perolehan tersebut, prediksi menggunakan fuzzy inference system dengan penentuan interval dengan metode kuartil dan desil memperoleh evaluasi cukup.
Tabel 9. Hasil Prediksi
Nama Metode Metode Desil Metode Kuartil
MAPE
26.43 %
28.77 %
Prediksi permintaan dengan fuzzy inference system diawali dengan proses penentuan himpunan fuzzy, dan dilanjutkan dengan proses pembentukan interval untuk setiap himppunan fuzzy. Dalam penentuan interval dilakukan dengan metode kuartil serta metode desil. Setelah ditentukann interval, dilakukan proses perhitungan fuzzy inference engine model mamdani terhadap 84 data histori. Berdasarkan perhitungan tersebut diperoleh hasil prediksi dengan mean absolute percentage error sebesar 26.43 % untuk metode desil, serta 28.77 % untuk metode kuartil. Evaluasi hasil penerapan fuzzy inference system model mamdani dengan penentuan interval himpunan menggunakan metode kuartil maupun metode desil dalam prediksi permintaan sediaan farmasi di puskesmas diperoleh hasil kompetensi prediksi cukup. Yang mana berdasarkan hasil penelitian diketahui bahwa interval dari himpunan fuzzy memberikan pengaruh terhadap kompetensi prediksi yang dihasilkan. Untuk penelitian selajutnya diharapkan dapat meneliti pengaruh instrumen penelitian seperti bentuk representasi jumlah himpunan fuzzy, maupun pengaruh desil yang digunakan terhadap hasil prediksi yang diperoleh.
Daftar Pustaka
-
[1] Kementrian Kesehatan Republik Indonesia, Standar Pelayanan Kefarmasian Di Puskesmas,
Peraturan. Jakarta: Berita Negara Republik Indonesia Tahun 2017 Nomor 206, 2017.
-
[2] N. Febriany, “Implementatiton of fuzzy time series methods,” J. Math., pp. 29–49, 2016.
-
[3] A. Sukoco and R. Yuli Endra, “Penerapan Fuzzy Inference System Metode Mamdani Untuk
Pemilihan Jurusan,” J. Manaj. Sist. Inf. dan Teknol., pp. 89–99, 2016.
-
[4] C. P. P. Maibang and A. M. Husein, “Prediksi Jumlah Produksi Palm Oil Menggunakan Fuzzy
Inference System Mamdani,” J. Teknol. dan Ilmu Komput. Prima, vol. 2, no. 2, p. 19, 2019, doi: 10.34012/jutikomp.v2i2.528.
-
[5] A. A. I. D. Fibriayora, G. K. Gandhiadi, N. K. T. Tastrawati, and E. N. Kencana,
“APPLICATION OF MAMDANI FUZZY METHOD TO DETERMINE ROUND BREAD PRODUCTION AT PT VANESSA BAKERY,” vol. 8, no. 3, pp. 204–210, 2019.
-
[6] K. Harefa, “Penerapan Fuzzy Inference System untuk Menentukan Jumlah Pembelian Produk
Berdasarkan Data Persediaan dan Penjualan,” J. Inform. Univ. Pamulang, vol. 2, no. 4, p. 205, 2017, doi: 10.32493/informatika.v2i4.1487.
-
[7] M. B. S. Junianto, “Fuzzy Inference System Mamdani dan the Mean Absolute Percentage
Error (MAPE) untuk Prediksi Permintaan Dompet Pulsa pada XL Axiata Depok,” J. Inform. Univ. Pamulang, vol. 2, no. 2, p. 97, 2017, doi: 10.32493/informatika.v2i2.1511.
-
[8] J. G. Nayak, L. G. Patil, and V. K. Patki, “Groundwater for Sustainable Development
Development of water quality index for Godavari River ( India ) based on fuzzy inference system,” Groundw. Sustain. Dev., vol. 10, no. December 2019, p. 100350, 2020, doi:
10.1016/j.gsd.2020.100350.
This page is intentionally left blank.
488
Discussion and feedback