Design Of Hybrid Cryptography With Vigenere Cipher And RSA Algorithm On IOT Data Security

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 8, No 4. May 2020

Design of Hybrid Cryptography With Vigenere Cipher and RSA Algorithm On IOT Data Security

Maria Okta Safira^a1, I Komang Ari Mogi ^a2

^aInformatics Engineering,Faculty of Math and Science, University of Udayana South Kuta, Badung, Bali, Indonesia

• ¹    [email protected]

• ²    [email protected]

Abstract

In this paper two methods are used, namely the vigenere cipher method and the RSA method. The vigenere cipher method is an example of a symmetric algorithm, while RSA is an example of an asymmetric algorithm. The combination of these two methods is called hybrid cryptography which has the advantage in terms of speed during the encryption process. Each process, which is encryption and decryption, is carried out twice, so that security can be ensured. In the process of forming the key used the RSA method. In the encryption process using public keys that have been generated before when the key is formed. This public key is used in sending data to the recipient of a secret message where this key is used for the data encryption process. The Secret key is kept and will be used during the decryption process. There is a system architecture that describes how clients and servers communicate with each other over the internet using the TCP protocol where the client here is an IoT device and the server is a server.

Keywords: RSA method, Vigenere Cipher Method, Hybrid Cryptography, IoT, Data Security.

• 1.    Introduction

The development of technology every year continues to grow, many emerging new innovations related to technology. This can be proven in our daily activities where we can easily find any technology that is around us, such as the use of electronic goods, digital goods and the latest technology, namely IoT (internet of things) by utilizing sensors and the internet as a connecting each device. This technology was created to simplify work, save time and save energy. Besides the positive impact of this technology is created is easier to communicate so that they can exchange information or data with each other without worrying about long distances. In this modern era different cities, countries and even different continents is not the biggest obstacle in communication, information exchange and data exchange. But there are also concerns about data security during the data exchange process because there are private data that cannot be spread widely. Examples of such personal data are personal information such as health information, information related to a country's defense and security, and other personal information. If this information or personal data is widespread, it can be detrimental to an individual or group. One way that can protect data security so that it remains safe is to secure existing data using cryptography.

In cryptography there are two important things that must be done including the encryption process and the decryption process. The encryption process is a process in which the information or data sent is converted into an unknown form by applying certain algorithms. Data that can be understood is usually called a plaintext and data that is in a

different and incomprehensible form is called a ciphertext. While the decryption process is a process in which data or information that has been previously changed into an unknown form is changed back to the initial data or information submitted. Many cryptographic algorithms can be used in implementing data security. Cryptographic algorithms are divided into two types based on the type of key used, namely the symmetric algorithm and the asymmetric algorithm. Asymmetric algorithms use different keys during the encryption process and the decryption process. In the symmetric algorithm there are two types of keys namely public keys and secret keys. The symmetric algorithm is inversely proportional to the asymmetric algorithm, which uses the same key for the encryption process and the decryption process.

There are several studies related to data security on IoT, one of which is the title "Data Security on Internet Devices of Things Using the Public Key Cryptography Method" which uses the Public Key Cryptography method with the RSA algorithm as an algorithm used for key generation, encryption, and decryption of data which exists. From the conclusion of the study it was found that the test results from the use of the RSA algorithm can run well even though it takes a lot of time and memory and the authors suggest going forward to use hybrid encryption methods in order to ensure data security on Internet of Things devices (Sembiring).

In another research on hybrid cryptography with the title "Hybrid Cryptographic Design Combination of Vigenere Cipher and Elgamal Methods in Securing Secret Messages" it is said that hybrid cryptography is often used because it utilizes the superior speed of data processing by symmetric algorithms and the ease of key transfers using asymmetric algorithms. This results in increased speed without reducing comfort and safety (Bella Ariska, 2018).

In research related to the RSA method with the title "Encryption and Description Using the RSA Algorithm" it is said that RSA is one of the strongest encryption algorithms where RSA has two keys namely private key and public key. In the process of making public and private keys, there are several factors to consider, namely the size of the key, the determination of the p and q values so they are difficult to break into, and the possible weaknesses that can be identified when the data is encrypted (Shodiq, 2016).

• 2.    Research Method

In matters regarding data security, the author will increase data security by using hybrid cryptography where in this cryptography will combine several algorithms including symmetry and asymmetrical algorithm which will increase security so that it becomes safer. The methods that will be used for this research are Vigenere Cipher and RSA. The Vigenere Cipher method is symmetrical and RSA is asymmetric. This research was conducted in accordance with the stages in the flowchart diagram for this paper. Problem identification is the stage of observation in the process of exchanging information on IoT. The focus of this research observation is the security issue of the exchange of information itself. The purpose of this observation is to identify problems according to existing problems.

Literature study is the stage of collecting material from various references and journals that are in accordance with the topic of the problem, namely the use of hybrid cryptography using the Vigenere Cipher and RSA method in securing IoT data. Problem analysis is the stage of analysis of security problems when the data exchange process occurs. In this analysis it is assumed that the sender and recipient are unaware of whether the data sent is safe and whether confidential or not is kept confidential. The solution to this problem is to do the encryption and description process using hybrid cryptography techniques with a combination of two methods namely Vigenere Cipher and RSA.

identification of problems

study of literature

problem analysis

the process of forming public keys and secret keys with the RSA method

Encryption process (public key) with the

Vigenere cipher and

RSA methods

Decryption process (secret key) with RSA method and Vigenere _v cipher,

Figure 1. research flowchart

• 2.1    Cryptography

Cryptography is a secret writing. Cryptography is the study of how to secure and protect data. There are terms commonly used in cryptography, namely plaintext (M) is the message to be sent (in the form of original data), ciphertext (C) is the encrypted message and the result of encryption. Encryption is the process of converting plaintext into ciphertext and decryption is a process that converts ciphertext into plaintext which is initially in the form of different data from initial data to original / original data, and key is a number that is kept secret and used in the encryption and decryption process.

Cryptographic algorithms can be divided into two types based on the type of key used, the symmetric algorithm and the asymmetric algorithm. Asymmetric algorithms use different keys during the encryption process and the decryption process. In the symmetric algorithm there are two types of keys namely public keys and secret keys. The symmetric algorithm uses the same key for the encryption process and the decryption process. In cryptography itself there are two important things namely the encryption process and the decryption process. The encryption process is a process in

which the information or data sent is converted into an unknown form by applying certain algorithms. Data that can be understood is usually called a plaintext. Data that has a different and incomprehensible form is called a ciphertext. The decryption process is the process by which data or information that was previously transformed into an unknown form is converted back into the initial data or information submitted.

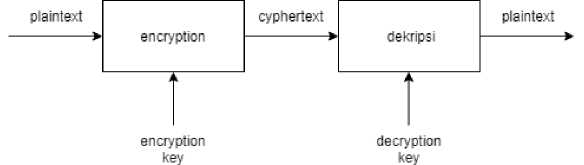
Figure 2. Diagram of the encryption and decryption process

• 2.2    Symmetric Algorithm and The Asymmetric Algorithm

Symmetric algorithm is an algorithm where the encryption key used is the same as the decryption key. Before sending data, the sender and recipient must choose a certain key that is the same to be shared and this key must be secret so that this algorithm is commonly called the secret key algorithm.

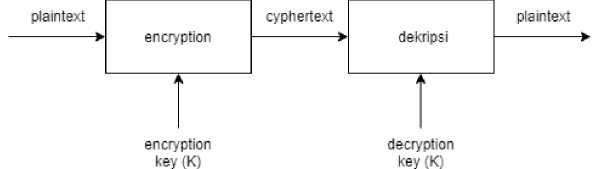
Figure 3. Diagram of the encryption and decryption process on a symmetric algorithm

Asymmetric algorithm is an algorithm where the encryption key used is not the same as the decryption key. In this algorithm uses two keys namely public key and private key. The public key is shared publicly while the private key is kept secret by the user. The public key is used as an encryption key while the private key is used as the decryption key.

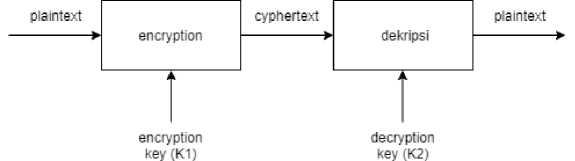
Figure 4. Diagram of the encryption and decryption process on a asymmetric algorithm

• 2.3    RSA Method
  
  2.3.1    Key Formation Process

The RSA method was created by 3 researchers from the Massachusetts Institute of Technology (MIT) namely Ron Rivest, Adi Shamir and Leonard Adleman in 1977. The quantities used in the RSA algorithm include

1.	p and q prime numbers	(secret)
2.	n = p x q	(not secret)
3.	φ W = ⅛ - 1) × ( <7 - 1)	(secret)
4.	e (encryption key)	(not secret)
5.	d (decryption key)	(secret)
6.	m (plaintext)	(secret)
7.	c (cyphertext)	(not secret)

The RSA algorithm's key generation process has two different keys for the encryption and decryption process. As for the steps related to the calculation of key determination, encryption, decryption are as follows:

• 1.    Determine 2 prime numbers, with names p and q

• 2.    Calculate the modulus value (n) with the formula n = p × q.

• 3.    calculate the total value or phi (φ) of n.

• 4.    Determine the value of e where the value of e is a prime number and the value of e must be in accordance with the terms 1 <e <φ (n). To prove the value of e can be calculated using the formula gcd (e, φ (n)) = 1.

• 5.    Finding the deciphering exponent value (d) with the formula d = (1 + (k × φ (n)) / e

• 6.    After finding the values of n, e, and d, the key pairs are public key pairs and secret key pairs. Public key pairs (n, e) and secret key pairs (n, d).

• 2.3.2    Encryption Process

In this process, a message is converted from plaintext into ASCII code using the ASCII table to see the code in accordance with existing plaintext. Next is to find the value of C using the formula c = m_l^e mod n. The key used in this process is the public key (n, e). From the calculation formula, we will find the value of c (cyphertext). The following is a picture from the ASCII table.

ASCII table

Char	Dec	Oct	Hex	I Char	Dec	Oct	Hex I	Char	Dec	Oct	Hex I	Char	Dec	Oct	Hex
(∏ul)	0	0000	0x00	I (=pl	32	0040	0x20 I	@	64	0100	0x4 0 I		96	0140	0x60
(soh)	1	0001	0x01	I	33	0041	0x21 j	A	65	0101	0x41 j	a	97	0141	0x61
(StX)	2	00 02	0x02	,l	34	0042	0x22 j	B	66	0102	0x42 I	b	98	0142	0x62
(etx)	3	00 03	0x03	I #	35	0043	0x23 j	C	67	0103	0x4 3 I	c	99	0143	0x63
(eot)	4	00 04	0x04	I $	36	0044	0x24 j	D	68	0104	0x44 j	d	100	0144	0x64
(eng)	5	0005	0x05	*	37	0045	0x25 j	E	69	0105	0x4 5 j	e	101	0145	0x65
(ack)	6	00 06	0x06	I &	38	0046	0x26 j	F	70	0106	0x46 I	f	102	0146	0x66
(bel)	7	0007	0x07		39	0047	0x27 j	G	71	0107	0x47 j	g	103	0147	0x67
(bs)	θ	0010	0x08	I (	40	0050	0x28 j	H	72	OllO	0x4 Q I	h	104	0150	0x68
(ht}	9	0011	0x09	I )	41	0051	0x29 j	Z	73	0111	0x4 9 j		105	0151	0x69
(∏1)	10	0012	OxOa		42	0052	0x2a j	J	74	0112	0x4 a I	j	106	0152	0x6a
(Vt)	11	0013	OxOb	+	43	0053	0x2b I	K	75	0113	0x4b I	k	107	0153	0x6b
(np)	12	0014	OxOc		44	0054	0x2 c j	L	76	0114	0x4 c j	1	108	0154	0x6c
(cr}	13	0015	OxOd	-	45	0055	0x2d I	M	77	0115	0x4 d I	πι	109	0155	0x6d
(so)	14	0016	OxOe		46	0056	0x2 e I	N	78	0116	0x4 e j	n.	110	0156	0x6e
(si)	15	0017	OxOf	I ∕	47	0057	0x2 f j	O	79	0117	0x4 f j	O	111	0157	0x6E
(die)	16	0020	OxlO	I 0	48	0060	0x30 j	P	80	0120	0x50 j	P	112	0160	0x70
(del)	17	0021	Oxll		49	0061	0x31 j	Q	81	0121	0x51 j	q	113	0161	0x71
(dc2)	lθ	0022	0X12	I 2	50	0062	0x32 j	R	82	0122	0x52 j	r	114	0162	0x72
(dc3)	19	0023	0X13	I 3	51	0063	0x33 j	S	83	0123	0x53 j	s	115	0163	0x73
(dc4)	20	0024	0x14	I 4	52	0064	0x34 j	T	84	0124	0x54 j		116	0164	0x74
(πak)	21	0025	0X15	5	53	0065	0x35 j	U	85	0125	0x55 j	U	117	0165	0x75
(syn)	22	0026	0x16	I 6	54	0066	0x36 j	V	86	0126	0x56 I	V	118	0166	0x76
(etb)	23	0027	0X17	I 7	55	0067	0x37 j	W	87	0127	0x57 j	W	119	0167	0x77
(can)	24	0030	0x18	8	56	0070	0x38 j	X	88	0130	0x58 j	X	120	0170	0x78
(eπι)	25	0031	0x19	I 9	57	0071	0x39 j	Y	89	0131	0x59 j	y	121	0171	0x79
(sub)	26	0032	Oxla		58	0072	0x3a j	Z	90	0132	0x5a j	Ξ	122	0172	0x7a
(esc)	27	0033	Oxlb		59	0073	0x3b I		91	0133	0x5b I		123	0173	0x7b
(fs}	28	0034	Oxlc		60	0074	0x3c j	∖	92	0134	0x5c j	I	124	0174	0x7c
(gs)	29	0035	Oxld	=	61	0075	0x3d I	]	93	0135	0x5d I		125	0175	0x7d
(rs)	30	0036	Oxle	⅛	62	0076	0x3 e I		94	0136	0x5e I		126	0176	0x7e
(us)	31	0037	Oxlf	I ’	63	0077	0x3 f j		95	0137	0x5f j	(del)	127	0177	0x7 f

Figure 5. The ASCII table

• 2.3.3    Decryption Process

In this process will change the ciphertext that has been obtained previously into the initial data in the form of plaintext. The decryption process is done by using a formula C=           . After finding the value of m by using

the calculation formula for decryption, it will also find the text of the message sent.

• 2.4    Vigenere Cipher Method

Vigenere cipher uses a substitution technique invented by Giovan Battista Bellaso in 1553. This Vigenere Cipher is a method designed to correct the weaknesses of a single substitution algorithm. Vigenere cipher is a technique of simpler cryptography that is safer. This method uses letter characters as the encryption key. Following are the letter characters used in the vigenere cipher method.

a	b	C	d	e	f		h	I		k	L	m	N
∣J	1	2	3	4	5	6	7	8	9	10	11	12	13
0	F		I	S		U	V	W	X	V	Z	A	B
14	15	16	17	18	19	20	21	22	23	24	25	26	27
C	D	E	F	G	H	I	J	K		M	N	O	P
28	29	30	31	32	33	34	35	36	37	38	39	40	41
Q	R	S	T	U	V	W	X	Y	Z	0	1	2	3
42	43	44	45	46	47	48	49	50	51	52	53	54	55
4	5	6	7	8	9	i	⅛	1		A	S	%	A
56	57	58	59	60	61	62	63	64	65	66	67	68	69
&	*	(	)			=	-I-	{	}		1
70	71	72	73	74	75	76	77	78	79	80	81	82	83
		<	>			7	∕
84	85	86	87	SS	89	90	91	92

Figure 6. The character table of the vigenere cipher method

The encryption process can be calculated using a formula

E_i =   + K_i mod 93.

Explanation:

Ei = Encryption caracter i

P_i = Characters in the message

Et =Key characters i

While the decryption process can be calculated using the formula

D₁ =   + K₁ mod 93.

Explanation:

Dt = Decryption caracter i

Ei =Key characters

Ei = Character in ciphertext

• 3.    Result and Discussion
  
  3.1    Hybrid Cryptography Implementation

Hybrid cryptography is a combination of several algorithms including symmetry and asymmetric algorithms which will increase the security of data. The methods to be used are Vigenere Cipher and RSA. The Vigenere Cipher method is symmetrical and RSA is asymmetric. Suppose that the message to be sent is "keuangan" where this message is a secret message that must not be spread. This message can only be read by the sender and recipient

• 3.1.1    Key Formation Process

In the process of forming this key using the RSA method to obtain public keys and secret keys where the secret key will only be stored by the sender of the message and the public key is sent to the recipient. Following are the key formation generated by the RSA method

• 1.    The first step that must be done is to determine two prime numbers with the names p and q with the condition p > q where p is 61 and q is 5.

• 2.    Next calculate the modulus or n value with the formula n = p × q where the values of p and q have been determined in the previous step n = p × q n = 61 × 5 n = 305

• 3.    Then calculate the total value or phi value of the modulus or value using the formula φ (n) = (p - 1) × (q - 1) φ (n) = (p - 1) × (q -1)

φ (n) = (61-1) ×(5-1)

φ (n) = 60 × 4

φ (n) =240

• 4.    The next step is to determine the value of e where the value of e is a prime number and 1 <e <φ (n) with the terms gcd (e, φ (n)) = 1. the value of e to be used is 17. To prove that 17 matches the condition existing evidence will be carried out as follows (17, 240) = 1 240 mod 17 = 2 17 mod 2 = 1 2 mod 1 = 0

• 5.    Then look for the deciphering exponent value (d) with the formula d = (1 + (k × φ (n)) / e, where k is any number until it produces an integer value by trying k = 1,2,3, ... After trying all numbers of 1, it was found that the value k = 8 because it produces an integer value.

d = (1 + (k × φ (n)) /e

d = (1 + (8 × 240) /17

d = (1 + 1920) / 17

d = 1921/17

d =113

• 6.    After finding the values of n, e, and d, the key pairs are found namely public key pairs and secret key pairs.

Public key pairs (n, e) = (305, 17)

Secret key pair (n, d) = (305, 113)

• 3.1.2    Encryption Process

In this encryption process, there are two stages: the first stage using the vigenere cipher method and the second stage using the RSA method. It was previously known that the message to be delivered was "keuangan" and the key to be used was the public key is (305, 17).

• 1.    Encryption by the Vigenere Cipher Method

plaintext = keuangan

public key = (305, 17)

Plaintext (P)	k	e	u	a	n	g	a	n
Index	10	4	20	0	13	6	0	13
Key (K)	3	0	5	,	1	7	3	0
Index	55	52	57	88	53	59	55	52
(P + K) mod 93	65	56	77	88	66	65	55	65
Ciphertext	@	4	+	,	#	@	3	@

Figure 7. Table of results of the ciphertext of the Vigenere Cipher

• 2.    Encryption by the RSA Method

The ciphertext results of the Vigenere Cipher method are encrypted again using the RSA method by using messages that have been encrypted by Vigenere Cipher namely @4+,#@3@. Then it will be translated in ASCII code. Following is a table of message conversions

i	character	Ciphertext (Mi)	ASCII
1	@	M1	64
2	4	M2	52
3	+	M3	43
4	,	M4	44
5	#	M5	35
6	@	M6	64
7	3	M7	51
8	@	M8	64

Figure 8. Table of message conversions into ASCII code

Then, the encryption process uses the RSA method. For this process, we must find the value of C, which is the ciphertext value generated from RSA encryption using the formula C= as in the table below.

i	Mi	Value C = Mie mod n
1	M1	174
2	M2	102
3	M3	218
4	M4	129
5	M5	250
6	M6	174

7	M7	246
8	M8	174

Figure 9. The encryption process uses RSA

• 3.1.3    Decryption Process

The decryption process is carried out in 2 stages, namely the first stage using the RSA method and the second stage using the vigenere cipher method. 1. Decryption process uses the RSA method

In this process the recipient of the message receives a message that has been previously encrypted by the sender and then must decrypt the ciphertext so that it can be read. The decryption process is done using a key that has been sought before. In this process the character results will be obtained namely @4+,#@3@. The following table is a calculation for the decryption process using the RSA method.

i	Ci	Value M = cid mod n	character
1	174	64	@
2	102	52	4
3	218	43	+
4	129	44	,
5	250	35	#
6	174	64	@
7	246	51	3
8	174	64	@

Figure 10. The decryption process uses RSA method

• 2.    Decryption process uses Vigenere Cipher

Previously obtained characters using the RSA method are @4+,#@3@. Next do the second stage decryption process using the vigenere cipher like the table below which will later get a hidden secret message that is "keuangan".

Cipherteks (P)	@	4	+	,	#	@	3	@
Indeks	65	56	77	88	66	65	55	65
Kunci (K)	3	0	5	,	1	7	3	0
Indeks	55	52	57	88	53	59	55	52
(C - K) mod 93	10	4	20	0	13	6	0	13
Plainteks	k	e	u	a	n	g	a	n

Figure 11. The decryption process uses Vigenere Cipher Method

• 3.2    System Architecture

The challenge in using RSA and Vigenere Cipher encryption lies in the efficiency of memory usage and the speed of the encryption process. The system architecture below illustrates how the client and server communicate through the

internet using the TCP protocol where the client here is an IoT device and the server is a server.

Figure 12. IoT server communication architecture

The stages of the encryption process in the system architecture include:

• 1.    The client opens a connection to the Server to receive public keys (n, e)

• 2.    The server sent a public key

• 3.    The client receives a public key

• 4.  The client does the plaintext encryption with the public key

• 5.  The client sends the encrypted ciphertext to the server

• 6.    The server accepts ciphertext and decrypts it using the private key

Figure 13. System Design

Data security is needed to keep the message confidential and can only be understood by the recipient and sender. This study uses the IoT tool as a client. The IoT device used is in the form of a sensor where this sensor will later capture information and data from the sender and will send it to the recipient of the message. After the sensor captures information, the sensor will send raw data to the CPU and the CPU will process the received data. The data will be encrypted to ensure its safety. This encryption process will produce ciphertext data and will be accepted by the server.

• 4.    Conclusion

In this study using hybrid cryptography by combining two methods, namely the RSA method and the vigenere cipher method. The RSA method plays a role in the formation of a key that is a public key and a secret key where both of these keys are used for encryption and decryption. Whereas the vigenere cipher method plays a role in the encryption and decryption of existing data. The combination of these two methods is able to overcome the problem of key distribution. Hybrid cryptography is considered safe because the encryption and decryption process is carried out twice. Hybrid cryptography is often used because it has advantages in terms of data processing speed and ease of transferring existing keys so that the combination of these two methods can be used for data security. However, there are challenges in the use of RSA and Vigenere Cipher encryption which lie in the memory usage efficiency and speed of the encryption process. By encrypting, data or messages sent can be guaranteed data security of IoT devices.

References

• [1] . Ariska, B., Suroso, S., & Endri, J. (2018). Rancangan Kriptografi Hybrid Kombinasi Metode Vigenere Cipher Dan Elgamal Pada Pengamanan Pesan Rahasia. Prosiding SENIATI, 4(2), 328-336.

• [2] . Marsel, S. A., & Irwan S. Keamanan data pada perangkat internet of things menggunakan metode public-key cryptography.

• [3] . Muhammad Shodiq. Enkripsi dan deskripsi menggunakan algoritma rsa. Jurnal Fakultas Teknik, 2016.

• [5] . Ardelia Nidya Agustina, A. & N. (2015). Pengamanan Dokumen Menggunakan Metode Rsa (Rivest Shamir Adleman ) Berbasis Web. 14–19.

• [6] . Prabowo, H. E., & Hangga, A. (2015). Enkripsi Data Berupa Teks Menggunakan Metode Modifikasi Vigenere Cipher. Seminar Nasional Aplikasi Teknologi Informasi (SNATi), 1–4.

485