Memodelkan Indeks Pembangunan Manusia Provinsi Bali dengan Regresi Data Panel

pISSN : 2301 - 8968

eISSN : 2303 - 0186

JEKT ♦ 12 [2] : 241-247

Memodelkan Indeks Pembangunan Manusia Provinsi Bali dengan Regresi Data Panel

Eka N. Kencana

Jurusan Matematika - FMIPA

Universitas Udayana

ABSTRAK

Tulisan ini ditujukan untuk memodelkan Indeks Pembangunan Manusia (IPM) dari 9 kabupaten/kota di Provinsi Bali menggunakan data IPM masing-masing kabupaten/ kota pada periode 2009-2014. Secara khusus tulisan ini diarahkan untuk (1) mengetahui kelayakan dari Common Effect dan Fixed Effect dalam memodelkan IPM, dan (2) mengidentifikasi variabel yang berpengaruh nyata terhadap besaran IPM. Hasil analisis membuktikan Fixed Effect memiliki kinerja yang lebih baik dibandingkan Common Effect dalam memodelkan IPM Provinsi Bali. Temuan lainnya, rata-rata lama bersekolah dan angka harapan hidup merupakan dua dari 17 variabel yang terbukti mempengaruhi IPM secara signifikan.

Kata kunci: harapan hidup, IPM, lama bersekolah, regresi data panel.

Klasifikasi JEL: O150, C510, C520.

Model the Bali Province Human Development Index with Panel Data Regression

ABSTRACT

This study is aimed to model Human Development Index (HDI) of Bali Province by applying panel data regression (PDR). HDI’s data of nine cities in Province of Bali for period 2009–2014 were used to demonstrate the ability of PDR to model. This research is directed to (1) determine which panel data regression model – Common Effect Model (CEM) vs Fixed Effect Model (FEM) – is more accurate to model the HDI’s data; and (2) to determine variable(s) that significantly affect the HDI’s. By utilizing 17 variables that are obtained from Statistics Office (BPS) of Bali, best model is developed. We concluded that FEM is more accurate than CEM in modelling HDI’s of Bali Province with coefficient of determination as much as 94.7 percent. In addition, two out of 17 variables i.e. the average length of time schooling and life expectancy proved significantly affect the HDI’s for all of cities in the Province of Bali.

Keywords: HDI, life expectancy, panel data, time schooling.

JEL classification: O150, C510, C520.

PENDAHULUAN

Gujarati & Porter (2009) mendefinisikan analisis regresi sebagai kajian terhadap hubungan sebuah variabel terjelaskan (variabel respon) dengan satu atau lebih variabel penjelas (variabel bebas) dengan maksud untuk menaksir dan/atau memprediksi nilai rata-rata hitung (mean) atau rata-rata populasi variabel respon menggunakan nilai-nilai pada variabel bebas yang telah diketahui/ ditetapkan.

Umumnya analisis regresi diaplikasikan pada matriks data cross-section, data yang diamati dengan mengabaikan dimensi waktu. Jika waktu dipertimbangkan sebagai salah satu sumber

keragaman matriks data, maka analisis regresi yang digunakan disebut Panel Data Regression (PDR) atau model Re-gresi Data Panel (RDP). Diperhitungkannya keragaman data karena pengaruh waktu membuat RDP diyakini mampu menghasilkan inferensia lebih informatif saat hubungan antarvariabel pada matriks data panel (panel data), gabungan antara data cross-section dengan data time series, dikaji.

Terdapat tiga bentuk RDP yang dapat dipilih dalam mengkaji hubungan antara variabel respon dengan variabel-variabel penjelasnya, yaitu Common Effect Model (CEM), Fixed Effect Model (FEM), dan Random Effect Model (REM). CEM

dan REM tidak membedakan intersep pada model antarindividu (cross-section) dan antarwaktu (timesection) amatan memperhatikan CEM menganggap intersep bernilai konstan, sedangkan REM lebih menitikberatkan pada dekomposisi error model. Pada FEM, perbedaan intersep antarindividu dan antarwaktu dihitung melalui penggunaan variabel dummy dan metode pendugaan parameter menggunakan teknik Least Square Dummy Variable (LSDV). Hal ini menyebabkan dari ketiga bentuk RDP, FEM dianggap memiliki kelebihan bila dibandingkan dengan CEM dan REM (Gujarati & Porter, 2009, p. 462).

RDP pada umumnya diaplikasikan untuk membangun model-model ekonometrika pada ranah ilmu ekonomi dan atau ilmu manajemen menggunakan pendekatan kuantitatif. Sebagai misal, untuk membedakan motivasi kerja karyawan yang berstatus tetap dengan karyawan yang berstatus outsourcing, Ratnasari et al. (2014) menggunakan RDP dengan FEM sebagai teknik analisisnya. Sebagai teknik statistika yang tergolong ke dalam kelompok dependency technique (Hair, Anderson, Tatham, & Black, 1995), RDP memiliki karakter analisis yang sama dengan analisis regresi, membedakan variabel-variabel model ke dalam kelompok variabel penjelas (dependent variable) dan variabel bebas (independent variables). Secara umum, bila i obyek diamati pada kurun waktu t, i = 1··· N dan t = 1··· T; model RDP dari y_i sebagai fungsi linier dari K variabel bebas x_k dapat dinyatakan dalam formulasi berikut (Hsiao, 2003, p. 12):

K

Sit ^{- α}it + ^^^ βkit ■ ^xkit ^^^ flit ...................(1)

k=l

Pada persamaan (1), y⅛ dan ^air masing-masing menyatakan nilai variabel terikat dan

konstanta model dari amatan ke-i pada waktu ke-t; β_ki_tadalah koefisien dari variabel bebas ke-k; x_kit adalah nilai variabel bebas ke-k dari amatan ke-i

pada waktu ke-t; dan μ_it menyatakan galat amatan pada individu ke-i di waktu ke-t.

Bila dicermati, pada dasarnya persamaan (1) menganggap seluruh koefisien regresi (α dan β) berbeda antarindividu dan antarwaktu amatan. Menurut Hsiao (2003), analisis data panel lebih sering dilakukan dengan mengasumsikan koefisien atau intersep bersifat konstan, melalui dua persamaan berikut yang diderivasi dari persamaan (1):

Yit — ^ai + ∑k=l Pk -Xkit + hit ...................(2)

Yu — ^ait ^+^ ∑k=l βk ■ ^xkit ^∣^ bit...................(3)

Persamaan (2) mengasumsikan nilai intersep bervariasi dengan koefisien dari x_k bernilai konstan antarindividu amatan, dan pada persamaan (3) nilai intersep bervariasi antarindividu dan antarwaktu amatan dengan koefisien dari x_k bernilai konstan.

Saat diasumsikan kedua parameter (intersep dan koefisien peubah bebas model) bernilai konstan antarindividu dan antarwaktu amatan, persamaan (1) akan berbentuk y_it = α + ∑*=₁β_lc -X_wr + μ_it; tidak berbeda dengan model persamaan regresi linier berganda. Model ini merupakan model tersederhana pada model RDP dan sering disebut dengan nama Common Effect Model (CEM). Pada CEM, parameter- parameter α dan β_k; k = 1 … K diduga menggunakan metode ordinary least square (OLS) seperti pada model regresi linier (Hsiao, 2003; Gujarati & Porter, 2009).

Ketika nilai intersep dari masing-masing individu diasumsikan berbeda dengan koefisien dari variabel-variabel bebas diasumsikan konstan di seluruh waktu amatan (time-section), persamaan (1) berbentuky_it = a_iΛ-∑^₁β_k .χ_tit + μ_it. Model RDP yang mengasumsikan intersep berbeda tetapi koefisien tetap disebut sebagai Fixed Effect Model (FEM). Menurut Gujarati & Porter (2009, p. 596), istilah ‘fixed-effect’ terkait dengan fakta bahwa meskipun intersep antarindividu berbeda, tetapi tetap bersifat konstan pada seluruh waktu amatan (time invariant).

Untuk menduga parameter α_i pada FEM, penggunaan dummy variable diintroduksi. Menggunakan dummy, FEM dengan slope tetap dapat dinyatakan sebagai:

y_it = «1 + ^.₌₂ ¾ D_ji + 2^β_kit χ_kit + μ_it>

• ₁        „ ∏; bilai = i.            _zjλ

dengan Dji ^o j IciiTiTiycL ................(4)

Sebagai contoh, FEM untuk RDP yang melibatkan 3 individu amatan (i = 1,2,3) dengan asumsi slope tetap tetapi intersep berbeda adalah:

K

y_it = «1 + α₂¾i + a₃D_3i + ∑ β_kit x_kit + μ_it.

k=l

Riset ini diarahkan untuk mengetahui model RDP yang paling cocok diterapkan untuk

Tabel 1. Daftar Variabel Penelitian

Kode Deskripsi
Y	Indeks Pembangunan Manusia
X1	Kepadatan penduduk per km2
X2	Angka melek huruf
X3	Rata-rata lama sekolah
X4	Angka harapan hidup
X5	Pengeluaran rata-rata per kapita per bulan
X6	Persentase rata-rata pengeluaran untuk konsumsi
X7	Persentase rumah tangga yang memiliki fasilitas air minum
X8	Persentase rumah tangga dengan jenis lantai bukan tanah
X9	Persentase rumah tangga dengan luas lantai < 20 m2
X10	Persentase rumah tangga dengan dinding tembok
X11	Persentase rumah tangga dengan sumber penerangan dari PLN
X12	Persentase rumah tangga dengan fasilitas BAB sendiri
X13	Persentase penduduk miskin
X14	Tingkat pengangguran terbuka
X15	Persentase penduduk dengan keluhan kesehatan sebulan sebelumnya
X16	Persentase penduduk dengan keluhan kesehatan dan kegiatannya terganggu
X17	Jumlah penduduk bekerja

Sumber: Analisis Data (2017)

memodelkan Indeks Pembangunan Manusia (IPM) Provinsi Bali. Sebagai salah satu provinsi di Indonesia, pada periode tahun 2010–2016 IPM Provinsi Bali senantiasa di atas IPM Indonesia. Pada periode tersebut, di tingkat nasional IPM Bali berada pada peringkat kelima setelah DKI Jakarta, DI Yogyakarta, Kalimantan Timur, dan Kepulauan Riau. BPS Indonesia mencatat IPM Bali pada tahun 2016 – menggunakan metode baru dalam penghitungan IPM – sebesar 73.65 sementara IPM Indonesia sebesar 70.18 (BPS Indonesia, 2017). Sebagai salah satu indikator makroekonomi, IPM lazim digunakan untuk ‘mengukur’ keberhasilan pembangunan di suatu wilayah. IPM juga merupakan proksi untuk menilai tingkat kesejahteraan masyarakat.

METODE PENELITIAN

Model RDP terbaik tentang IPM Provinsi Bali dibuat menggunakan data sekunder IPM dari 9 kabupaten/kota di Provinsi Bali periode 2009–2014 yang diperoleh dari Badan Pusat Statistik (BPS) Bali. Skor IPM dari 9 kabupaten/ kota (i = 1, …, 9) pada 6 tahun periode amatan (t = 1, …, 6) merupakan variabel terikat (y_it) dengan variabel bebas pada model berjumlah 17 (K = 17). Daftar variabel pada model RDP penelitian ini diperlihatkan pada Tabel 1.

Pengembangan dan pemilihan model RDP terbaik dalam memodelkan IPM Provinsi Bali menggunakan 17 variabel bebas pada Tabel 1 dilakukan melalui serangkaian tahapan analisis

berikut:

• 1.    membangun CEM dengan asumsi intersep model dari kabupaten/ kota di Provinsi Bali bernilai konstan di seluruh periode waktu pengamatan;

• 2.    melakukan Uji Chow untuk memeriksa asumsi bahwa intersep konstan antarwaktu amatan bisa diterima;^

• 3.    jika hasil Uji Chow menunjukkan sekurang-kurangnya terdapat satu kabupaten/kota dengan intersep berbeda, FEM dibentuk dengan mengasumsikan intersep antarkabupaten/kota berbeda, tetapi memiliki koefisien (slope) konstan pada setiap variabel bebas dalam model;

• 4.    memeriksa signifikansi koefisien dari masing-masing variabel bebas pada model yang terpilih; ⅛

• 5.    membangun ulang (re-modeling) model dengan melibatkan variabel yang terbukti signifikan sebagai model terbaik; dan ⅛

• 6.    mengintepretasikan model RDP terbaik yang diperoleh.

HASIL ANALISIS DAN DISKUSI

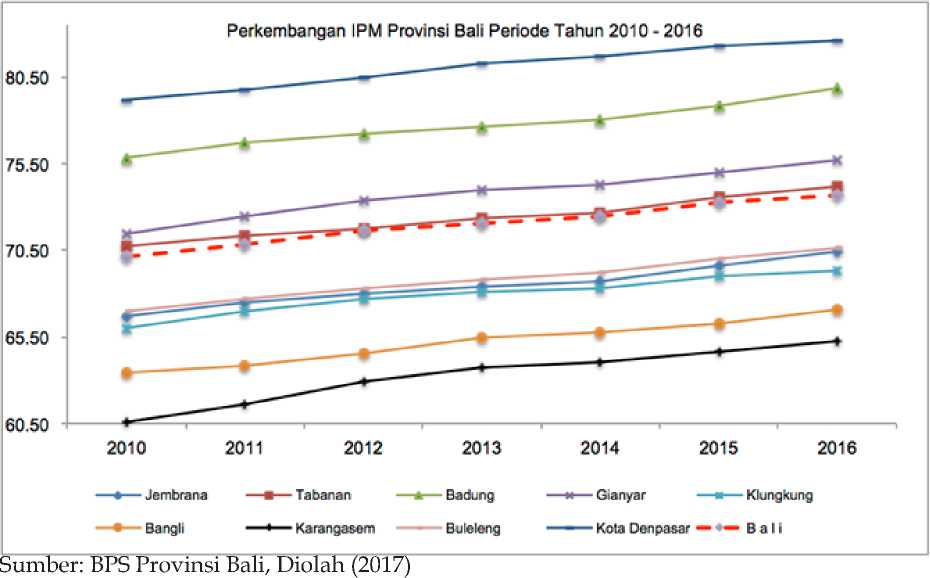
Gambar 1 menunjukkan perkembangan IPM dari 9 kabupaten/kota di Provinsi Bali pada periode 2010–2016:

Pada gambar 1 terlihat Kawasan Sarbagita (Denpasar, Badung, Gianyar, dan Tabanan) menduduki peringkat 1 hingga 4 dari 9 kabupaten/ kota di Provinsi Bali serta melebihi nilai IPM Bali pada periode tahun 2010-2016. Lima kabupaten lainnya memiliki nilai IPM di bawah nilai IPM Bali serta terindikasi membentuk dua kelompok:

Gambar 1. Perkembangan IPM Kabupaten/Kota di Provinsi Bali

• (a) kelompok I: Kabupaten Karangasem dan Bangli merupakan dua kabupaten dengan peringkat terbawah; (b) kelompok II: Kabupaten Klungkung, Jembrana, Buleleng memiliki kemiripan pada perkembangan nilai IPM.

Tahapan pertama dalam memilih model RDP terbaik adalah membangun CEM, yang bisa dinyatakan dalam persamaan berikut:

IPM₁= a + ∑^₁β_k.x_ki+ ε_i. (5)

Pada persamaan (5), nilai i = 1, …, 9 masing-masing menyatakan Kabupaten Jembrana, Tabanan, Badung, Gianyar, Klungkung, Bangli, Karangasem, Buleleng, dan Kota Denpasar. Melalui metode penduga OLS, hasil analisis CEM yang dilakukan menggunakan program EViews memberikan hasil seperti ditunjukkan pada Tabel 2.

Model RDP dengan pendekatan CEM pada Tabel 2 diperoleh dengan terlebih dahulu membakukan seluruh variabel bebas X k mempertimbangkan adanya perbedaan satuan pengukuran pada variabel model. Pemeriksaan terhadap koefisien-koefisien penduga menunjukkan hanya 5 variabel bebas (X2, X3, X4, X7, dan X12) yang memiliki nilai p < 0.05, 13 penduga lainnya tidak. Selain itu, nilai R²tinggi meski hanya 5 variabel bebas dengan koefisien penduga yang nyata, mengindikasikan adanya permasalahan multikolinearitas antarvariabel bebas.

Sebelum dilakukan tindakan remedial

terkait dugaan multikolinearitas variabel bebas, akan dilakukan Uji Chow untuk mengetahui kelayakan asumsi intersep tidak berbeda antarkabupaten/ kota.

Pada hakekatnya, Uji Chow digunakan untuk memeriksa kestabilan parameter-parameter sebuah model regresi (Hsiao, 2003; Gujarati & Porter, 2009). Menurut Gujarati & Porter (2009), saat sebuah model regresi yang melibatkan data deret waktu dibangun, ada peluang terjadinya perubahan struktural (structural change) pada hubungan kausal antara variabel terikat dengan variabel-variabel bebas. Perubahan struktural

ini bisa dimaknai sebagai akibat perubahan (ketakstabilan) parameter-parameter penduga model pada rentang waktu pengamatan, atau pada antarindividu bila matriks data merupakan data panel.

Untuk mengetahui kelayakan asumsi bahwa intersep model tidak berbeda antarkabupaten/kota, maka pasangan hipotesis yang diperiksa pada Uji Chow dapat dinyatakan sebagai:

H0

H1

oleh

a_i = a,-. V,_

• 3 α_j = α_j∙; V_j

  9

  9

  
  

Pada Uji Chow, penolakan H₀ ditentukan statistik F_{Cross-section} atau statistik χ²_{Cross-section}.

Hasil analisis memberikan nilai F

Cross-section (8,28) sebesar 1.871 dengan nilai p = 0.105 dan χ²_{Cross-section(8)} = 23.125 dengan nilai p = 0.003. Mencermati kedua nilai peluang ini, khususnya peluang dari

Tabel 2. Hasil Analisis (Pendekatan CEM)

Variabel	Koefisien	Simp. Baku	Statistik t	Nilai p
Konstan	72.634	0.124	583.812	0.000
X1	-0.640	0.362	-1.771	0.085
X2	-1.050	0.416	-2.250	0.016
X3	5.072	0.666	7.614	0.000
X4	1.014	0.260	3.902	0.000
X5	0.584	0.391	1.494	0.144
X6	0.472	0.363	1.303	0.201
X7	0.881	0.264	3.338	0.002
X8	0.440	0.437	1.006	0.321
X9	-0.506	0.459	-1.102	0.278
X10	-0.400	0.333	-1.202	0.237
X11	0.095	0.338	0.282	0.779
X12	-1.068	0.472	-2.264	0.030
X13	-0.070	0.327	-0.213	0.832
X14	-0.287	0.234	-1.228	0.228
X15	0.048	0.415	0.113	0.911
X16	0.262	0.453	0.557	0.567
X17	0.163	0.184	0.886	0.381
R2	0.959		Adjusted R2	0.939
Fhit	49.183		Durbin Watson	2.270
ung Nilai p	0.000		Nilai AIC	2.920

Sumber: Hasil Analisis (2017)

statistik χ², maka H₀ tidak dapat diterima yang berimplikasi setidak-tidaknya ada satu kabupaten/ kota yang intersepnya berbeda dengan kabupaten/ kota lainnya. Mempertimbangkan hal ini, maka model RDP dengan pendekatan CEM kurang layak diaplikasikan dan pendekatan FEM layak dipertimbangkan. Hasil analisis model RDP dengan pendekatan FEM menggunakan metode Least Square Dummy Variables (LSDV) diringkas pada Tabel 3.

Bila dibandingkan dengan pendekatan CEM, pendekatan FEM memberikan nilai koefisien determinasi (R²) yang lebih baik sebesar 97.2 persen, sedikit lebih besar dari R² pada CEM sebesar 95.9 persen. Meskipun demikian, juga terdeteksi adanya multikolinearitas mencermati nilai R² hanya disertai oleh dua variabel bebas dengan nilai p yang signifikan. Kondisi ini membutuhkan tindakan remedial, salah satunya mengeliminasi variabel bebas yang tidak signifikan dan model dianalisis ulang.

Mencermati nilai F_Hitung = 40.516 dengan nilai p = 0.000, model RDP melalui pendekatan FEM memiliki setidak- tidaknya satu penduga parameter model yang signifikan. Dibandingkan dengan pendekatan CEM, FEM memiliki nilai

Akaike Information Criterion (AIC) lebih kecil yang mengindikasikan FEM lebih layak (AIC_FEM = 2.789 < AIC_CEM = 2.920).

Menggunakan dua variabel bebas yang terbukti signifikan pada uji parsial model, X3 dan X4, maka pemodelan ulang RDP dengan pendekatan FEM dilakukan. Hasil analisis dengan hanya menyertakan X3 dan X4 pada model ditunjukkan pada Tabel 4.

Tabel 4 menunjukkan terjadi peningkatan nilai F_Hitung saat hanya dua variabel bebas disertakan dalam model. Meskipun nilai koefisien determinasi menurun menjadi 95.8 persen dari nilai sebelumnya sebesar 97.2 persen, nilai AIC menunjukkan model terakhir (AIC_FEM2 = 2.690) terbukti lebih baik dibandingkan dengan full model (AIC_FEM17 = 2.789). Merujuk Wagenmakers & Farrel (2004), model dengan nilai AIC yang lebih kecil lebih layak dibandingkan dengan model yang memiliki AIC lebih besar. Tabel 5 memberikan hasil komparasi kelayakan ketiga model RDP yang dibangun untuk memodelkan IPM Provinsi Bali.

Hasil komparasi model pada Tabel 5 menunjukkan nilai statistik Durbin-Watson (statistik d) pada model FEM₂ telah lebih kecil dari 2, sebagai nilai ambang atas yang mengindikasikan

Tabel 3. Hasil Analisis (Pendekatan FEM)

Variabel Koefisien		Simp. Statistik Baku        t	Nilai p
Konstan	72.634	0.114  637.810	0.000
X1	-0.364	0.840    -0.433	0.668
X2	-1.276	0.752    -1.698	0.101
X3	5.477	0.927     5.906	0.000
X4	1.802	0.534     3.374	0.002
X5	0.439	0.465     0.943	0.354
X6	0.262	0.405     0.647	0.523
X7	0.589	0.374     1.557	0.126
X8	0.303	0.492     0.616	0.543
X9	-0.395	0.817    -0.484	0.632
X10	-0.295	0.512    -0.576	0.569
X11	0.117	0.443     0.263	0.794
X12	-1.026	0.574    -1.789	0.085
X13	0.157	0.425     0.370	0.714
X14	-0.132	0.247    -0.535	0.597
X15	-0.521	0.467    -1.114	0.275
X16	0.065	0.488     0.133	0.895
X17	0.197	0.206     0.960	0.346
Efek Tetap pada Unit Cross-section
Jembrana	-0.437	Bangli	0.733
Tabanan	-0.908	Karangasem	1.583
Badung	-1.422	Buleleng	3.036
Gianyar	-1.209	Denpasar	-2.638
Klungkung	1.260
R2	0.973	Adjusted R2	0.949
F hitung Nilai p	40.516	Durbin Watson	2.319
	0.000	Nilai AIC	2.789
Sumber: Hasil Analisis (2017)
Tabel 4. Model Ulang (Pendekatan FEM)
Variabel Koefisien		Simp. Statistik Baku        t	Nilai p
Konstan	72.634	0.115  628.858	0.000
X3	5.684	0.743     7.649	0.000
X4	2.172	0.393     5.522	0.000
Efek Tetap pada Unit		Cross-section
Jembrana	0.050	Bangli	2.784
Tabanan	-2.000	Karangasem	6.050
Badung	-3.588	Buleleng	2.787
Gianyar	-2.079	Denpasar	-6.970
Klungkung	2.968
R2	0.958	Adjusted R2	0.948
F hitung Nilai p	96.889	Durbin Watson	1.863
	0.000	Nilai AIC	2.690

Sumber: Hasil Analisis (2017)

tidak terjadi autokorelasi derajat satu (first-order autocorrelation) pada galat model (Gujarati & Porter, 2009, pp. 467-468). Hasil komparasi juga menunjukkan adanya penurunan nilai AIC secara konsisten pada pendekatan CEM hingga FEM dengan hanya menyertakan variabel bebas yang signifikan pada full model dari FEM. Fakta lainnya, Kawasan SARBAGITA yang secara

Tabel 5. Komparasi Model RDP dari IPM

Variabel	Koefisien
	CEM	FEM17	FEM2
Konstan	72.634	72.634	72.634
X1	-0.640	-0.364	–
X2	-1.050	-1.276	–
X3	5.072	5.477	5.684
X4	1.014	1.802	2.172
X5	0.584	0.439	–
X6	0.472	0.262	–
X7	0.881	0.589	–
X8	0.440	0.303	–
X9	-0.506	-0.395	–
X10	-0.400	-0.295	–
X11	0.095	0.117	–
X12	-1.068	-1.026	–
X13	-0.070	0.157	–
X14	-0.287	-0.132	–
X15	0.048	-0.521	–
X16	0.262	0.065	–
X17	0.163	0.197	–
Efek Tetap pada Unit Cross-section
Jembrana	–	-0.437	0.050
Tabanan	–	-0.908	-2.000
Badung	–	-1.422	-3.588
Gianyar	–	-1.209	-2.079
Klungkung	–	1.260	2.968
Bangli	–	0.733	2.784
Karangasem	–	1.583	6.050
Buleleng	–	3.036	2.787
Denpasar	–	-2.638	-6.970
R2	0.959	0.973	0.958
Adjusted R2	0.939	0.949	0.948
Nilai F Hitung	49.183	40.516	96.889
Nilai p	0.000	0.000	0.000
Nilai AIC	2.920	2.786	2.690
Durbin Watson	2.270	2.319	1.863

Sumber: Hasil Analisis (2017)

relatif memiliki pertumbuhan ekonomi yang lebih baik dibandingkan dengan lima kabupaten lainnya, memiliki nilai efek tetap absolut yang lebih tinggi, berturut-turut tertinggi pada Kota Denpasar diikuti Kabupaten Badung, Gianyar, dan Tabanan.

Bila koefisien variabel-variabel bebasnya diperiksa, terlihat pengaruh rata-rata lama sekolah (X3) lebih dominan dibandingkan pengaruh angka harapan hidup (X4) terhadap IPM dari masing-masing kabupaten/kota di Provinsi Bali. Kedua variabel mampu menjelaskan keragaman IPM sebesar 95.8 persen. Terjadinya peningkatan 1 satuan (dalam bentuk terstandarisasi) dari X3 atau 1 satuan X4 menyebabkan meningkatnya IPM masing-masing kabupaten/kota sebesar slope dari setiap variabel ini.

Signifikannya dua variabel bebas di atas dalam menentukan IPM kabupaten/kota di Provinsi Bali sesuai dengan metode penghitungan IPM yang dilakukan BPS Indonesia. BPS Indonesia (2017) telah menyesuaikan metode penghitungan IPM Indonesia mulai tahun 2014 dengan menggunakan 3 indikator utama: (a) Angka Harapan Hidup Saat Lahir; (b) Harapan Lama Sekolah dan Rata-rata Lama Sekolah; serta (c) Pengeluaran per Kapita Disesuaikan. Peneliti menduga lebih dominannya rata-rata lama sekolah disebabkan penghitungan agregasi untuk indikator ini telah menggunakan rataan aritmatika dari rataan geometrik yang digunakan sebelum tahun 2014.

SIMPULAN DAN REKOMENDASI

Simpulan

Penelitian ini menyimpulkan, terkait dengan penerapan analisis regresi data panel untuk memodelkan IPM dari kabupaten/kota di Provinsi Bali, pen- dekatan FEM lebih layak digunakan dengan mengeliminasi sejumlah variabel bebas untuk menghilangkan pengaruh multikolinearitas antarvariabel. Dari dua variabel bebas yang berpengaruh signifikan terhadap IPM, angka rata-rata lama sekolah memiliki pengaruh lebih dominan dibandingkan pengaruh dari angka harapan hidup.

Rekomendasi

Studi ini hanya mengelaborasi dua dari empat jenis pendekatan yang tersedia pada analisis regresi data panel. Disarankan penelitian lainnya diarahkan untuk mengetahui kinerja 2 pendekatan lainnya, intersep dan slope yang tidak bersifat time invariant serta tidak konstan antarindividu amatan.

REFERENSI

Hair, J., Anderson, R., Tatham, R., & Black, W.

(1995). Multivariate Data Analysis with Readings (fourth ed.). New Jersey: Prentice-Hall, Inc.

Ratnasari, N. M., Kencana, E. N., & Gandhiadi, G. K. (2014). Aplikasi Regresi Data Panel dengan Pendekatan Fixed Effect Model (Studi Kasus: PT. PLN Gianyar). e-Jurnal Matematika , 3 (1), 1-7.

Wagenmakers, E., & Farrel, S. (2004). AIC model selection using Akaike weights. Psychonomic Bulletin & Review , 11 (1), 192-196.

Hsiao, C. (2003). Analysis of Panel Data (2nd Ed. ed.). Cambridge: Cambridge University Press.

Gujarati, D. N., & Porter, D. J. (2009). Basic Econometrics (5th Ed. ed.). New York: The McGraw-Hill/ Irwin.

BPS Indonesia. (2017). Indeks Pembangun an Manusia Menurut Provinsi, 2010 - 2016.

247