Pemodelan Regresi Panel pada Data Pendapatan Asli Daerah (PAD) Terhadap Dana Alokasi Umum (DAU)

Written by Rezzy Eko Caraka
on February 04, 2019

pISSN : 2301 - 8968

eISSN : 2303 - 0186

JEKT ♦ 12 [1] : 55-61

Pemodelan Regresi Panel Pada Data Pendapatan Asli Daerah (PAD) Terhadap Dana Alokasi Umum (DAU)

Rezzy Eko Caraka

ABSTRAK

Data panel adalah gabungan dari data time series (antar waktu) dan data cross section (antar individu/ ruang). Untuk menggambarkan panel data secara singkat, misalkan pada data cross section, nilai dari satu variabel atau lebih dikumpulkan untuk beberapa unit sampel pada suatu waktu waktu. Dalam panel data, unit cross section yang sama di-survey dalam beberapa waktu.Regresi data panel digunakan untuk menentukan model regresi yang paling sesuai digunakan untuk memodelkan pendapatan asli daerah (PAD) terhadap dana alokasi umum (DAU) untuk tujuh kabupaten/kota provinsi Jawa Tengah anggaran 2008-2010. Model yang dihasilkan dengan REM didapat nilai R² sebesar 43,8893% Pendapatan Asli Daerah (PAD) dipengaruhi oleh Dana Alokasi Umum (DAU), sedangkan sisanya dipengaruhi oleh faktor lain.

Kata kunci: Fixed Effect; Common Effect Model; Random Effect Model; PAD; DAU

Panel Regression Modeling on Regional Original Revenue Data (PAD) Against General Allocation Funds (DAU)

ABSTRACT

Data panel is a composite of the data time series (over time) and cross section (between individuals / space). To describe briefly the data panel,egg in cross section,and the value of one or more variables were collected for the sample unit at a time of time. In panel data, the same cross section units surveyed in some time. Panel data regression was used to determine the most appropriate regression model is used to model local revenue (PAD) of the general allocation fund (DAU) for seven districts / cities in Central Java province from 2008 to 2010 budgets. Models produced by REM obtained R² values of 43.8893 % revenue (PAD) is influenced by the General Allocation Fund (DAU), while the rest influenced by other factors.

Keywords: Fixed Effect; Common Effect Model; Random Effect Model; PAD; DAU

1. PENDAHULUAN

Pemerintah daerah dalam melaksanakan rumah tangganya memerlukan sumber pendapatan yang berasal dari PAD. Tanpa adanya dana yang cukup, maka ciri pokok dari otonomi daerah menjadi hilang. Meskipun daerah juga mendapatkan sumber-sumber dari PAD, namun PAD mempunyai peranan yang strategis di dalam keuangan daerah karena bagi suatu daerah sumber pendapatan daerah merupakan tiang utama penyangga kehidupan daerah. Oleh karena itu para ahli sering memakai PAD sebagai alat analisis dalam menilai tingkat otonomi suatu daerah. Dalam kegiatan untuk memajukan daerah oleh pemerintah pusat menyiapkan alokasi dana untuk membiayai progran dan kegiatan pemerintah daerah secara berkesinambungan. Pembiayaan yang berkesinambungan tersebut dialokasikan

dalam kelompok pendanaan rutin yang terdapat dalam APBD (Anggaran Pendapatan dan Belaja Daerah), maka pendanaan tersebut merupakan salah satu anggaran dalam APBD untuk melaksanakan kegiatan pembangunan untuk kesejahteraan rakyat. Apabila suatu daerah baik secara finansial, oleh pemerintah pusat dana tersebut dialokasikan ke daerah lain yang masih tertinggal. Jika penerimaan PAD telah mencapai 20% dari pengeluaran daerah, maka sumber keuangan daerah sudah dapat dikatakan cukup, sehingga ketergantungan pemerintah daerah terhadap pemerintah pusat kecil. Jadi semakain besar persentase PAD terhadap pengeluaran daerah, maka otonomi daerah dapat dikatakan semakin baik.Agar daerah dapat mengurus rumah tangganya sendiri dengan sebaik-baiknya, maka kepadanya perlu diberikan sumber-sumber pembiayaan yang cukup.

e-mail: rezzyekocaraka@gmail.com

55

Namun mengingat tidak semua sumber-sumber pembiayaan dapat diberikan kepada daerah maka kepada daerah diwajibkan untuk menggali segala sumber keuangannya sendiri berdasarkan peraturan perundangan-undangan yang berlaku (Machfud Sidik dan Soewondo, 2001).

Dalam Undang-Undang Nomor 33 Tahun 2004 disebutkan bahwa sumber penerimaan daerah dalam pelaksanaan desentralisasi, diklasifikasikan dalam 3 sumber, yaitu: PAD (Pendapatan Asli Daerah); Dana Perimbangan; dan Lain-lain Penerimaan yang sah. Khusus mengenai PAD dapat dikatakan bahwa peranannya/ sumbangannya terhadap keseluruhan APBD masih relatif kecil. Potensi PAD masing-masing daerah sangat jauh berbeda, sehingga menimbulkan terjadinya fiscal gap. Fiscal gab terjadi karena karakteristik daerah di Indonesia sangat beraneka ragam, ada darah yang memiliki kekayaan alam yang sangat melimpah, ada juga daerah yang tidak memiliki kekayaan alam yang besar tetapi karena struktur ekonomi yang telah tertata dengan baik, maka potensi pajak dapat dioptimalkan sehingga daerah tersebut menjadi kaya, dalam artian PAD tinggi. Di sisi lain ada juga daerah yang secara alamiah maupun struktur ekonomi masih sangat tertinggal.

2. TINJAUAN PUSTAKA
- 2.1. Dana Alokasi Umum

Dalam Undang-Undang Nomor 33 Tahun 2004 tentang Perimbangan Keuangan Antara Pusat dan Pemerintahan Daerah, Dana Alokasi Umum (DAU) didefinisikan sebagai dana yang bersumber dari pendapatan APBN yang dialokasikan dengan tujuan pemerataan kemampuan keuangan antarDaerah untuk mendanai kebutuhan Daerah dalam rangka pelaksanaan Desentralisasi. DAU dimaksudkan untuk mengurangi ketimpangan kemampuan keuangan antar daerah melalui penerapan formula dengan mempertimbangkan kebutuhan dan potensi daerah.

2.2. Pendapatan Asli Daerah

Pendapatan Asli Daerah (PAD) adalah pendapatan yang diperoleh Daerah yang dipungut berdasarkan Peraturan Daerah sesuai dengan peraturan perundang- undangan. Pendapatan Asli Daerah (PAD) bersumber dari Pajak Daerah;Retribusi Daerah; hasil pengelolaan kekayaan Daerah yang dipisahkan; dan lain-lain PAD yang sah (meliputi hasil penjualan kekayaan Daerah yang tidak dipisahkan;jasa giro;pendapatan 56

bunga;keuntungan selisih nilai tukar rupiah terhadap mata uang asing; dan komisi, potongan, ataupun bentuk lain sebagai akibat dari penjualan dan/atau pengadaan barang dan/atau jasa oleh Daerah)

2.3. Data Panel

Data panel atau panel data adalah gabungan dari data time series (antar waktu) dan data cross section (antar individu/ ruang). Untuk menggambarkan panel data secara singkat, misalkan pada data cross section, nilai dari satu variabel atau lebih dikumpulkan untuk beberapa unit sampel pada suatu waktu waktu. Dalam panel data, unit cross section yang sama di-survey dalam beberapa waktu (Gujarati, 2003).Regresi dengan menggunakan panel data, memberikan beberapa keunggulan dibandingkan dengan pendekatan standar cross section dan time series.

1. Keunggulan dan Permasalahan Regresi dengan Data Panel, Hsiao (1986) mencatat bahwa penggunaan panel data dalam penelitian ekonomi memiliki beberapa keuntungan utama dibandingkan data jenis cross section maupun time series; dapat memberikan peneliti jumlah pengamatan yang besar, meningkatkan degree of freedom (derajat kebebasan), data memiliki variabilitas yang besar dan mengurangi kolinieritas antara variabel penjelas, di mana dapat menghasilkan estimasi ekonometri yang efisien.
2. Panel data dapat memberikan informasi lebih banyak yang tidak dapat diberikan hanya oleh data cross section atau time series saja.
3. Panel data dapat memberikan penyelesaian yang lebih baik dalam inferensi perubahan dinamis dibandingkan data cross section.

Di samping berbagai keunggulan dimiliki model panel data tersebut, ada beberapa permasalahan yang muncul dalam pemanfaatan data jenis panel, yaitu permasalahan autokorelasi dan heterokedastisitas. Sementara itu ada permasalahan baru yang muncul seperti korelasi silang (cross-correlation) antar unit individu pada periode yang sama.

2.3.1 Common Effect Model

Pendekatan pertama ini merupakan pendekatan paling sederhana yang disebt estimasi CEM atau pooled least square. Menurut Sukendar dan Zainal (2007), pada pendekatan ini diasumsikan bahwa nilai intersep masing-masing variabel adalah sama, begitu pula slope koefisien untuk semua unit cross-section dan time

series. Berdasarkan asumsi ini, maka model CEM dinyatakan sebagai berikut (Widarjono,2007)

yit = α + β’ xit + uit i=1,2,…,N; t=1,2…T (1)

Asumsi ini menawarkan kemudahan, namun model mungkin mendistorsi gambaran yang sebenarnya dari hubungan antara Y dan X antar unit cross-section.

2.3.2 Fixed Effect Model

Model dikenal sebagai model fixed effect karena meskipun intersep berbeda untuk setiap unit cross-section tapi masih mengasumsikan slope koefisien tetap. Model FEM dapat dinyatakan yit = α + β’ xit + uit i=1,2,…,N; t=1,2… (2)

2.3.3 Random Effect Model

Pada model REM, diasumsikan α_imerupakan variabel random dengan mean α_o. Sehingga intersep dapat dinayatak sebagai α_i = α₀ + ε_i dengan ε_i merupakan error random yang mempunyai mean 0 dan varians σ_ε2, ε_i tidak secara langsung diobservasi, atau disebut juga variabel laten. Jadi, persamaan model REM adalah sebagai berikut:

yit = α + β’ xit + wit i=1,2,…,N; t=1,2…T (3)

Dengan w_it = ε_it + u_it. Suku error gabungan w_it memuat dua komponen error yaitu ε_i komponen error cross-section danu_ityang merupakan kombinasi komponen error cross-section dan time series. Karena inilah, REM juga disebut Error Components Model (ECM). Beberapa asumsi yang berlaku pada REM adalah:

ε_i~N(0,σo),u_it^N(0,σo),E(ε_i,u_it) = O,E(ε_i,ε_j) = O (i ≠ j),

E(u_it,u_is) = E(U_itlU_jt) = E(U_itjU_js)U_it = O (i ≠ j),

Yaitu bahwa komponen error individu tidak saling berkorelasi dan tidak berautokorelasi antar unit cross-section dan time series.

2.4. Pemilihan Model

Untuk mengetahui metode yang paling sesuai dapat dilakukan dengan Uji Hausmann, Uji Lagrange Multiplier (LM), dan Uji Chow.Uji Haussman digunakan untuk memilih antara Fixed effect Model(FEM) atau Random Effect Model (REM). Hipotesis dari uji Haussman adalah:

H0 : estimator random konsisten

H1 : estimator random tidak konsisten

Di mana Ho diterima artinya REM lebih baik digunakan daripada FEM, dan sebaliknya. Maka Ho diterima/ ditolak jika:

X²_tab>X²_hit Ho diterima atau

X²_tab<X²_hit Ho ditolak

Untuk mendapatkan nilai X²_hit diambil dari

perbedaan nilai beta dan covarian setiap metode. Uji statistik Haussman yang dapat dilakukan adalah (Haussman, 1978):

I_{w =} (ThEM-PremY /4) (v(βFEM)~^v(βREM)}

dan untuk multivariate,

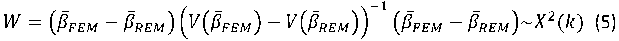
Uji statistik Haussman ini mengikuti

distribusi chi-square (X²) dengan degrees of freedom sebanyak k di mana k adalah jumlah variabel independen. Jika nilai statistik Haussman lebih besar dari nilai kritisnya maka model yang tepat adalah FEM, sedangkan sebaliknya bila nilai statistik Haussman lebih kecil dari nilai kritisnya maka model yang tepat adalah REM. Menurut Judge (1985), ada beberapa hal yang harus diperhatikan untuk menentukan pendekatan mana yang dipilih (FEM atau REM) dalam estimasi panel data, yaitu:

- Jika ε dan X berkorelasi, maka lebih baik menggunakan FEM, dan jika ε dan X tidak berkorelasi, maka lebih baik digunakan REM
- Jika T (jumlah time series) besar dan n (jumlah individu/ unit) kecil, perbedaan keduanya relatif kecil, maka lebih baik menggunakan FEM
- Jika n besar dan T kecil, digunakan FEM apabila unit tidak random dari sampel yang besar dan digunakan REM apabila unit diambil secara random
- Jika n besar dan T kecil dan apabila asumsi REM terpenuhi, estimator REM lebih efisien dibandingkan FEM

Uji chow digunakan untuk memilih model antara common effect dengan fixed effect.

- Jika Ho diterima, maka model pool (common).
- Jika Ho ditolak, maka model fixed effect

Uji Lagrange Multiplier (LM) digunakan untuk memilih antara OLS tanpa variabel dummy atau memilih random effect. Uji Lagrange Multiplier (LM) yang dapat dilakukan adalah (Breusch dan Pagan, 1980):

LM = ^- (⅜⅛⅛ -

2(τ-i)∖∑p=₁∑JL₁⅛ /

(6)

dengan:

n : jumlah individu

T : jumlah periode waktu

e : residual metode OLS

Jika perhitungan LM>X2 dengan satu derajat kebebasan, maka Ho ditolak, artinya REM bisa digunakan untuk mengestimasi persamaan regresi.

Uji statistik F digunakan untuk memilih

antara metode PLS tanpa variabel dummy atau

memilih fixed effect. Uji statistik F yang dapat

dilakukan adalah sebagai berikut:

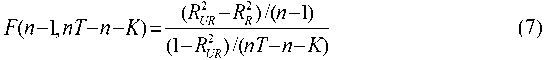
dengan:

R²ur : mengacu pada unrestricted model

R²r : mengacu pada restricted model

n : jumlah unit cross section

T : jumlah unit waktu

K : jumlah parameter yang akan diestimasi Jika ternyata hasil perhitungan F stat ≥ F

(n-1,nT-n-K), berarti Ho ditolak, artinya intersep untuk semua cross section tidak sama. Dalam hal

ini, FEM digunakan untuk mengestimasi persamaan regresi. Sementara itu, hal-hal yang harus diperhatikan jika menggunakan FEM (Kumastuti, 2008). Pertama, penggunaan variabel dummy akan menimbulkan masalah degrees of freedom. Kedua, kemungkinan terjadi multikolienaritas. Ketiga, FEM tidak bisa digunakan untuk mengetahui dampak variabel yang invariant. Keempat, error term harus diperhatikan sehingga asumsi klasik error term harus dimodifikasi.

R² adalah perbandingan antara; variabel dependen yang dijelaskan oleh variabel-variabel independen. Selain variabel-variabel indepanden tersebut yang juga berpengaruh terhadap DPK dimasukkan dalam variabel E, atau yang sering disebut dengan standar eror. R² akan bernilai 1 jika dijumlahkan dengan E. Semakin besar nilai R², maka model tersebut dikatakan tepat atau dapat dipercaya Hasil ini dapat diterima jika uji F menunjukkan nilai yang besar/ signifikan. Jadi, keputusan untuk menerima dan menggangap suatu model sebagai model yang benar dan dapat dipercaya harus dilihat bersama-sama antara besarnya nilai F dan R². R² dirumuskan dengan

Di mana Y adalah Y estimasi atau estimasi garis regresi dan Y adalah nilai Y rata-rata, yang diperoleh dengan memasukkan nilai parameter vaiabel independen, dan harga variabel independen tersebut.

3. METODE PENELITIAN

Data yang digunakan dalam membangun model adalah data time series sejak tahun 2008

– 2012, dan data cross section yang terdiri dari 7 kabupaten di provinsi Jawa Tengah meliputi Cilacap, Banyumas, Purbalingga, Banjarnegara, Kebumen, Purworejo, dan Wonosobo. Dianalisis menggunakan data panel dengan software E-views.

4. HASIL DAN PEMBAHASAN
- 4.1 Common Effect Model (CEM)

Common Effect Model merupakan metode yang paling sederhana. Hasil analisis regresi dianggap berlaku untuk semua objek pada semua waktu. Berdasarkan output diperoleh nilai koefisien parameter constan -60332559 sedangkan koefisien parameter DAU 0,244456. Sehingga diperoleh model CEM sebagai berikut :