Peramalan Produk Domestik Regional Bruto (PDRB) Provinsi Bali Triwulanan (Q-to-Q) Tahun Dasar 2010 dengan Model Arima
on
pISSN : 2301 - 8968
eISSN : 2303 - 0186
JEKT ♦ 11 [1] : 63-72
Peramalan Produk Domestik Regional Bruto (PDRB) Provinsi Bali Triwulanan (Q-To-Q) Tahun Dasar 2010 Dengan Model Arima
Briliana Wellyanti
ABSTRAK
Produk Domestik Bruto Regional (PDRB) merupakan salah satu indikator kemajuan suatu wilayah/ daerah. Pertumbuhan ekonomi merupakan perbandingan PDRB di periode saat ini terhadap periode sebelumnya. Dalam perencanaan daerahnya (RPJMD), pemerintah daerah membutuhkan ramalan pertumbuhan ekonomi dalam kurun waktu 5 tahun ke depan. Dalam hal ini ramalan PDRB dapat diperoleh dengan berbagai metode, salah satu metode yang akan dibahas dalam penelitian ini adalah ramalan PDRB Bali dengan menggunakan metode ARIMA. Data yang digunakan adalah data PDRB Bali Triwulan I tahun 2007 sampai dengan triwulan II tahun 2016. Adapun metode analisis yang digunakan adalah analisis data time series yakni model ARIMA. Hasil penelitian menunjukkan bahwa model ARIMA mampu meramalkan PDRB Bali sampai dengan triwulan IV 2018. Adapun model ARIMA terbaik adalah model ARIMA (3,1,0).
Kata kunci: PDRB, Peramalan PDRB, ARIMA, Time series Analysis
Forecasting Bali Province Gross Regional Domestic Product (GRDP) Quarterly (Q-To-Q) 2010 with Arima Model
ABSTRACT
Gross Regional Domestic Product (GDRP) is one indikator of the progress of an area / region. Economic growth is a comparison of the GDRP in the current period against the previous period. In the planning area (RPJMD), local governments need economic growth forecast in the next 5 years. In this case the GDRP forecast may be obtained by various methods, one of the methods that will be addressed in this study is the GDRP forecast Bali using ARIMA. Bali’s GDRP on First Quarter of 2007 to the second quarter of 2016 is obtained from Statistik Bali. The analytical method used is the analysis of time series data that ARIMA models. The results showed that the ARIMA model is able to predict the GDP Bali until the fourth quarter 2018. The best ARIMA model is ARIMA (3,1,0).
Keywords: GDRP, Forecast, ARIMA, Time series Analysis
PENDAHULUAN
Perencanaan pembangunan ekonomi, memerlukan bermacam data statistik sebagai dasar berpijak dalam menentukan strategi kebijakan, agar sasaran pembangunan dapat dicapai dengan tepat. Strategi dan kebijakan yang telah diambil pada masa masa lalu perlu dimonitor dan dievaluasi hasil hasilnya. Berbagai data statistik yang bersifat kuantitatif diperlukan untuk memberikan gambaran tentang keadaan pada masa yang lalu dan masa kini, serta sasaran sasaran yang akan dicapai pada masa yang akan datang. Salah satu data statistik yang penting dibutuhkan dalam rangka perencanaan pembangunan ekonomi adalah data PDRB (Produk Domestik Bruto). Dari besaran PDRB dapat diturunkan indikator lain seperti pertumbuhan ekonomi.
Pertumbuhan Ekonomi dapat diartikan sebagai suatu ukuran kuantitatif yang menggambarkan perkembangan suatu perekonomian dalam suatu tahun tertentu dibandingkan dengan tahun sebelumnya (Sudono Sukirno, 2006 : 9). Suatu perekonomian dikatakan mengalami pertumbuhan jika jumlah produksi barang dan jasa yang dihasilkan meningkat. Tingkat pertumbuhan ekonomi yang tinggi dan berkesinambungan merupakan kondisi yang diinginkan setiap negara dan daerah. Angka pertumbuhan yang tinggi menunjukkan adanya peningkatan ketersediaan lapangan kerja dan pendapatan yang pada akhirnya diharapkan akan meningkatkan kesejahteraan dan kemakmuran masyarakat secara keseluruhan.
Pemerintah daerah dalam hal ini selalu
e-mail: briliana@bps.go.id
63
dituntut untuk membuat suatu Rancangan Pembangunan Jangka Menengah (RPJMD) daerah. PDRB dan pertumbuhan ekonomi menjadi salah satu indikator yang wajib ada dalam RPJMD tersebut. Dalam hal ini Pemerintah Daerah wajib membuat ramalan angka PDRB dan pertumbuhan ekonomi untuk kurun waktu 5 tahun yang akan datang.
Sehubungan dengan latar belakang diatas, maka tujuan dalam penelitian ini adalah untuk membuat model estimasi PDRB Provinsi Bali dari triwulan I tahun 2007 sampai dengan triwulan II tahun 2016, dengan model ARIMA, dan membuat ramalan PDRB Provinsi Bali triwulan III tahun 2016 sampai dengan triwulan IV tahun 2018.
KAJIAN PUSTAKA
PDRB (Produk Domestik Bruto)
Produk Domestik Regional Bruto (PDRB) merupakan nilai tambah bruto seluruh barang dan jasa yang tercipta atau dihasilkan di wilayah domestik suatu negara yang timbul akibat berbagai aktivitas ekonomi dalam suatu periode tertentu tanpa memperhatikan apakah faktor produksi yang dimiliki residen atau non-residen. Penyusunan PDRB dapat dilakukan melalui 3 (tiga) pendekatan yaitu pendekatan produksi, pengeluaran, dan pendapatan yang disajikan atas dasar harga berlaku dan harga konstan.
PDRB atas dasar harga berlaku atau dikenal dengan PDRB nominal disusun berdasarkan harga yang berlaku pada periode penghitungan, dan bertujuan untuk melihat struktur perekonomian. Sedangkan PDRB atas dasar harga konstan disusun berdasarkan harga pada tahun dasar dan bertujuan untuk mengukur pertumbuhan ekonomi.
Metode Penghitungan PDRB
Penghitungan PDRB dilakukan dengan 3 pendekatan yakni : 1) Pendekatan produksi (production approach), 2) Pendekatan pengeluaran (expenditure approach) dan 3) Pendekatan pendapatan (income approach).
Pendekatan dari segi produksi adalah menghitung nilai tambah dari barang dan jasa yang diproduksi oleh seluruh kegiatan ekonomi dengan cara mengurangi output dari masing-masing sektor atau sub sektor dengan biaya antaranya. Pendekatan ini bisa juga disebut pendekatan nilai tambah. Nilai tambah merupakan nilai yang ditambahkan pada barang dan jasa yang dihasilkan oleh unit produksi 64
dalam proses produksi dari input antara yang dikeluarkan untuk menghasilkan barang dan jasa tersebut. Nilai yang ditambahkan ini sama dengan balas jasa faktor produksi atas ikut sertanya dalam proses produksi.
Dalam pendekatan pendapatan ini, nilai tambah dari setiap kegiatan ekonomi dihitung dengan jalan menjumlahkan semua balas jasa faktor produksi yaitu upah dan gaji, surplus usaha, penyusutan dan pajak tidak langsung neto. Untuk sektor pemerintahan dan usaha-usaha yang sifatnya tidak mencari untung, surplus usaha tidak diperhitungkan. Yang termasuk dalam surplus usaha adalah bunga, sewa tanah dan keuntungan. Metode pendekatan pendapatan ini banyak dipakai pada sektor yang produksinya berupa jasa seperti sektor pemerintahan.
Pendekatan dari segi pengeluaran bertitik tolak pada penggunaan akhir barang dan jasa di wilayah domestik. Jadi Produk Domestik Regional dihitung dengan cara menghitung berbagai komponen pengeluaran akhir yang membentuk Produk Domestik Regional Bruto tersebut.
PDRB Tahun Dasar 2010
Perubahan tahun dasar Produk Domestik Bruto (PDB) merupakan suatu proses yang lazim dilakukan oleh kantor statistik suatu negara untuk menggambarkan kondisi perekonomian terkini. BPS telah melakukan perubahan tahun dasar PDB sebanyak 5 (lima) kali yaitu pada tahun 1960, 1973, 1983, 1993, dan 2000. Saat ini, BPS sedang melakukan proses penyusunan perubahan tahun dasar PDB dari tahun 2000 menjadi 2010. Sejalan dengan PDB, PDRB pun memerlukan penyesuaian ke tahun dasar yang baru yakni 2010.
Adapun tahun 2010 dipilih sebagai tahun dasar baru menggantikan tahun dasar 2000 karena beberapa alasan diantaranya Perekonomian Indonesia maupun wilayah lain di Indonesia relatif stabil di tahun 2010; Telah terjadi perubahan struktur ekonomi selama 10 (sepuluh) tahun terakhir terutama dibidang informasi dan teknologi serta transportasi yang berpengaruh terhadap pola distribusi dan munculnya produk-produk baru; Rekomendasi PBB tentang pergantian tahun dasar dilakukan setiap 5 (lima) atau 10 (sepuluh) tahun dan Adanya pembaharuan konsep, definisi, klasifikasi, cakupan, sumber data dan metodologi sesuai rekomendasi dalam SNA 2008.
Kerangka Konsep Penelitian METODE PENELITIAN
Data Penelitian
Penelitian ini menggunakan data sekunder yakni data PDRB Konstan Provinsi Bali Tahun Dasar 2010 dari Triwulan I 2007 sampai Triwulan II 2016. Adapun data sekunder tersebut diperoleh dari website BPS Provinsi Bali.
Teknik Analisis Data
Analisis yang digunakan dalam penelitian ini adalah analisis data time series yakni menggunakan model ARIMA atau metode Box dan Jenkins. Box dan Jenkins mempopulerkan metode peramalan data time series yang terdiri dari 3 tahapan yakni identifikasi model, estimasi parameter dan peramalan. Peramalan (forecasting) dengan menggunakan data time series (time series) secara sederhana sering dilakukan dengan analisis regresi linier. Namun agar hasil peramalan lebih akurat, terutama untuk data time series yang cukup panjang, maka data time series dapat dianalisis dengan mempertimbangkan berbagai perilaku data melalui berbagai model antara lain model autoregressive (AR), moving average (MA) dan autoregressive moving average (ARIMA) (Ghozali, 2007), yang dijelaskan sebagai berikut.
Autoregresive (AR)
Misalkan Yt adalah PDRB pada waktu t. Jika kita membuat model Yt sebagai:
(Yt - δ) = α1(Yt-1 - δ) + µ1 ...................................(1)
Dimana δ adalah mean dari Y dan µt adalah error term yang tidak berkorelasi dengan mean = nol dan variance (σ2) konstan ( white noise), maka kita dapat mengatakan Yt mengikuti pola stochastic first order autoregressive atau AR(1). Disini nilai Y pada waktu t tergantung dari nilai periode waktu sebelumnya ditambah dengan error term. Dengan kata lain nilai peramalan Y pada waktu t merupakan proporsi (α1) dari nilai Y pada waktu (t-1) ditambah random shock atau residual pada waktu t. Hal ini dapat diperlihatkan model: (Yt - δ) = α1(Yt-1 - δ) + α2(Yt-2 - δ) + µ1 ..................(2)
Model dengan nilai Y pada waktu t tergantung dari nilai Y pada waktu dua periode masa lalu disebut juga second order autoregressive process atau AR(2). Dalam hal ini nilai Y dinyatakan disekitar nilai mean δ. Secara umum model autoregressive dapat dituliskan:
(Yt - δ) = α1(Yt-1 - δ) + α2(Yt-2 - δ) + αp(Yt-p - δ) + µ1 ..................(3)
Dimana adalah pola autoregresif order
ke-p (pth-order autoregressive process atau AR(p).
Moving Average (MA)
Selain melalui proses model autoregresif (AR), memprediksi nilai Y juga dapat dilakukan melalui proses model moving average (MA). Model ini memanfaatkan u yang merupakan white noise stochastic error. Contoh model MA ditunjukkan sebagai berikut:
Yt = u + β0ut + β1ut-1 .............................................(4)
Dalam hal ini u adalah konstanta, dan Y pada waktu t sama dengan konstanta ditambah moving average dari error sekarang dan error masa lalu. Model seperti ini disebut Y mengikuti first order moving average process atau MA(1), dan untuk second order moving average process atau MA(2) ditunjukkan dengan model:
Yt = u + β0ut + β1ut-1+ β2ut-2.................................(5)
Secara umum model moving average (MA) pada order ke-p ditunjukkan dengan model:
Yt = u + β0ut + β1ut-1+ β2ut-2+ βput-p......................(6)
Pola Autoregresive dan Moving Average (ARMA)
Memprediksi nilai Y juga dapat dilakukan melalui proses Autoregresive dan Moving average (ARMA). Hal ini dimungkinkan karena Y juga memiliki karakteristik AR dan MA. Untuk model ARMA(1,1), maka proses peramalan atau prediksi terhadap Yt dapat dinotasikan sebagai berikut: Yt = θ + αYt-1 + | β0ut + β1ut-1 ...............................(7)
Nilai θ merupakan konstanta, dan model 2.7 merupakan model ARMA dengan satu autoregressive dan satu moving average. Peramalan secara umum dapat dilakukan dengan p autoregressive dan q moving average yang diringkas menjadi ARMA(p,q).
Pola Autoregresive Integreting Moving Average (ARIMA)
Seperti telah dijelaskan sebelumnya, bahwa model dengan menggunakan data time series (time series) diasumsikan dalam kondisi stationer, yang mana mean dan variance adalah konstan, serta covariance adalah time-invariant. Namun harus dimaklumi bahwa banyak data ekonomi time series tidak bersifat stationer atau integrated. Demikian juga telah dipahami bahwa jika data time series intergrated pada order 1 atau 1(1), maka nilai difference pertama atau 1(0) adalah stationer. Dengan cara yang sama jika data time series adalah 1(2), maka nilai difference kedua adalah 1(0). Secara umum dapat dikatakan bahwa jika data time series I(d), setelah di difference
sebanyak d kali akan didapatkan 1(0) seri.
Oleh karena itu jika data time series didifference sebanyak d kali untuk mendapatkan data stationer kemudian diaplikasikan pada model ARMA(p,q), maka model ini disebut Autoregresive Integrated Moving average atau ARIMA (p,d,q). Dalam hal ini p adalah jumlah autoregressive, d jumlah (berapa kali) data harus didifference agar data menjadi stationer, dan q adalah jumlah moving average. Dengan demikian ARIMA(2,1,2) berarti data time series yang didifference sekali (d= 1), memiliki dua autoregressive dan dua moving average. ARIMA(p,d=0,q) merupakan ARMA(p,q), ARIMA(p,0,0) sama dengan AR(p) dan ARIMA(0,0,q) sama dengan MA(q).
Tahapan Motode Box-Jenkins (BJ)
Suatu data time series perlu dilacak apakah data ini mengikuti pola AR (jika ya, berapa nilai p) atau mengikuti pola MA (dan jika ya, harus diketahui berapa nilai q) atau mengikuti pola ARMA (jika ya, harus diketahui berapa nilai p dan q), atau mengikuti pola ARIMA (jika ya, harus diketahui berapa nilai p, d, dan q. Oleh karena itu, untuk menjawab pertanyaan ini dapat dilakukan dengan metode Box-Jenkins. Metode ini terdiri dari empat langkah, yaitu:
Identifikasi: yaitu menentukan nilai yang tepat p, d, dan q dengan cara mengamati correlogram dan partial correlogram. Identifikasi ARIMA untuk PDRB dapat dilakukan dengan melihat correlogram dan partial correlogram data yang stationer. Untuk melihat kestasioneran data yang dapat dilakukan dengan melihat nilai autocorrelation (AC). Untuk pola yang white noise, maka nilai autocorrelation pada berbagai lag akan mempunyai nilai yang mendekati nol. Pengujian dilakukan dengan joint hypothesis bahwa semua koefisien autokorelasi sampai lag tertentu secara simultan sama dengan nol. Hal ini dapat dilakukan dengan menggunakan Q statistik yang dikembangkan oleh Box dan Pierce yang didefinisikan sebagai berikut
Q = n∑p2k..................................(8)
A-=I
Dimana n = sample size dan m = panjang lag. Q statistik sering digunakan untuk menguji apakah data time series dalam kondisi white noise atau tidak. Dengan menggunakan sample besar, distribusi Q statistik mendekati distribusi chi-square dengan degree of freedom sebesar m. Varians dari Box-
Pierce Q statistik diperbaiki oleh Ljung-Box yang dikenal dengan (LB) statistik yang didefinsikan:
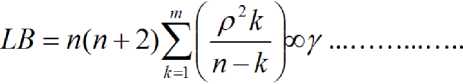
Nilai Q dan LB statistik pada sample besar mengikuti distribusi Chi-square dengan derajat bebas m, tetapi LB statistik lebih baik dari pada Q statistik untuk sample kecil. Untuk mendeteksi distribusi suatu data yang stasioner ataukah tidak, dapat juga dilihat dari grafik autocorrelation function (ACF) apakah melewati batas interval konfidensi. Konsep terkini yang banyak dipakai untuk menguji kestasioneran data time series adalah uji akar unit (unit root test) atau dikenal juga dengan uji Augmented Dickey Fuller (ADF). Seperti telah dijelaskan sebelumnya, bahwa data bersifat stasioner adalah data dengan perilaku data yang memiliki varians yang tidak terlalu besar dan mempunyai kecenderungan untuk mendekati nilai rata-ratanya. Dalam hal ini persamaan yang
digunakan adalah:
Yt - Yt-1 = ρYt-1Yt-1 + µt ...........................(10)
= (ρ-1)Yt-1 + µt
Atau dapat ditulis:
ΔYt = ρYt + µt ...................................................(11)
Dimana: δ = (ρ-1) adalah first difference
Analisis dilakukan dengan membuat regresi antara (first different) dan sehingga akan didapat koefisien regresinya, yaitu . Regresi metode yang sama secara parsial juga akan dilakukan terhadap semua variabel independen yang digunakan. Jika tidak signifikan berarti, maka data tidak stationer.
Selanjutnya untuk mendeteksi apakah pola AR atau MA atau ARIMA dapat digunakan pedoman Tabel 1.
Estimasi Model Tentatif: setelah menentukan nilai p dan q yang sesuai, langkah berikutnya adalah mengestimasi parameter autoregressive dan moving average yang dimasukkan dalam model.
Diagnostic Checking: setelah memilih model ARIMA dan setelah mengestimasi parameter, langkah selanjutnya adalah menguji apakah model ARIMA yang telah dipilih fit (cocok atau sesuai) karena mungkin ada model ARIMA lainnya yang lebih fit dengan data yang ada. Jadi Model ARIMA Box-Jenkins lebih condong pada seni daripada science. Keahlian diperlukan dalam memilih model ARIMA tepat. Salah satu cara menguji model yang terpilih adalah dengan
Tabel 1. Jenis Model Peramalan dengan Melihat Pola AC dan PAC
|
Jenis Model |
PolaAC |
Pola PAC |
|
AR(p) |
Menurun secara exponential |
Menurun drastis pada lag tertentu |
|
MA(q) |
Menurun drastis pada lag tertentu |
Menurun secara exponential |
|
ARMA(p,q) |
Menurun secara exponential |
Menurun secara exponential |
Sumber: Widarjono, 2013
melihat nilai residual yang diestimasi dari model adalah white noise. Jika jawabannya ya, maka kita menerima model yang fit, tetapi jika jawaban tidak, harus memulai lagi dari awal. Sehingga metode BJ merupakan proses iterasi.
Memilih Model ARIMA. Pada suatu saat peneliti dihadapkan pada dilema, misalnya dua model ARIMA yang dibuat sama baiknya berdasarkan metode sebelumnya. Untuk memilih model yang terbaik dari beberapa model yang baik, perkenalkan Akaike Information Criterion (AIC) yang dikembangkan oleh Prof. Harotugu Akaike, dan juga Bayesian Information Criteria (BIC) yang dikembangkan oleh Schwarz. Oleh karena dikembangkan oleh Schwarz, maka model BIC juga disebut model SIC. Semakin kecil nilai AIC, BIC atau SIC semakin baik model yang dibuat.
Peramalan: salah satu alasan penting popularitas dari model ARIMA adalah keberhasilannya didalam peramalan. Pada banyak kasus peramalan yang didapat dari metode ARIMA lebih reliabel atau handal daripada peramalan yang didapat dari mode tradisional, khususnya untuk peramalan jangka pendek.
HASIL DAN PEMBAHASAN
PDRB Bali Triwulanan
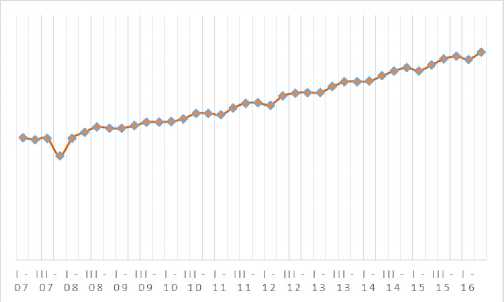
Selama hampir 10 tahun terakhir kondisi ekonomi Bali selalu tumbuh ke arah positif. Hal ini terbukti dari tren PDRB Konstan nya yang memiliki kecenderungan meningkat. Hal tersebut terlihat dari grafik I di bawah ini.
Total ekonomi Bali yang tercipta di Bali di triwulan II 2016 adalah Rp.33.992.354,02 juta. Nilai ini meningkat hampir 70 persen jika dibandingkan dengan PDRB Bali pada triwulan I 2007 yakni yang hanya sebesar Rp. 19.997.688,04 juta.
Jika dilihat tren pertumbuhan nya, maka pertumbuhan ekonomi Bali (y-on-y) selama hampir 10 tahun terakhir ini berada di kisaran 3-8
persen. Adapun pertumbuhan tertinggi adalah pada triwulan I tahun 2009 yakni mencapai 8,25 persen. Sedangkan pertumbuhan ekonomi Bali pada triwulan II tahun 2016 tercatat sebesar 6,53 persen.
PDRB Konstan Provinsi Bali (juta Rp) Triwulan I 2007 – Triwulan II 2016
Uji Kestasioneran Data
Data time series yang akan dianalisis haruslah bersifat stasioner. Suatu data dikatakan bersifat stasioner jika data tersebut memiliki varian yang tidak terlalu besar dan memiliki kecenderungan untuk mendekati nilai rata-ratanya. Ada beberapa cara yang digunakan untuk menguji kestasioneran data diantaranya adalah: 1) metode grafik, 2) correlogram, dan metode akar unit (unit root test).
Metode Grafik
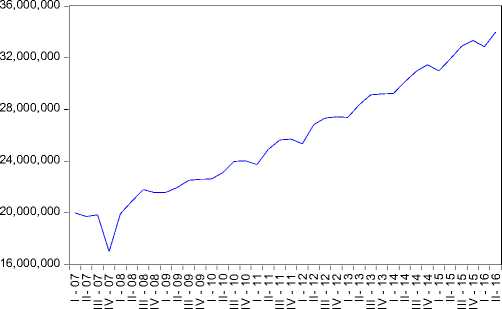
Suatu data dikatakan bersifat stasioner adalah ketika grafik nya menggambarkan sebaran data tersebut berada di antara rata-rata atau tidak membentuk tren tertentu. Jika dilihat berdasarkan grafik di bawah ini, maka PDRB Bali memiliki tren tertentu. Dari hal tersebut dapat disimpulkan bahwa data time series PDRB Bali tidak stasioner. Adapun kelemahan dari metode grafik ini adalah sifatnya yang subjekif, sehingga bisa saja tiap pengguna berbeda dalam menginterpretasi hasilnya. Metode selanjutnya yang digunakan dalam penentuan stasionaritas data adalah metode
Grafik 2.
Perkembangan PDRB Bali Triwulan I 2007 – Triwulan II 2016
PDRB
correlogram.
Metode Correlogram
Salah satu uji formal dalam penentuan stasionaritas data adalah metode correlogram. Untuk data yang stasioner, korelogram menurun dengan cepat seiring dengan meningkatnya lag. Sedangkan untuk data yang tidak stasioner, korelogram cenderung tidak menuju nol (turun lambat).
Berdasarkan hasil output di bawah ini, terlihat bahwa nilai autocorrelation function (AC) mengalami penurunan secara lambat sampai lag 16 (default). Selain itu jika dilihat dari nilai Prob. nya, maka secara individu signifikan secara statistik berbeda dari nol. Keadaan seperti ini
memperlihatkan bahwa data time series PDRB pada level nya tidak stationer. Karena dengan melihat grafik dan correologram masih bersifat subjektif, salah satu uji lainnya yang dapat digunakan untuk melihat kestasioneran data adalah Uji Akar Unit.
Unit Akar Unit (Unit Root Test)
Uji lainnya yang dilakukan untuk stasionaritas data adalah uji akar unit (Unit Root Test). Uji ini juga dikenal dengan uji Augmented Dickey-Fuller (ADF). Seperti telah dijelaskan sebelumnya, bahwa data bersifat stasioner adalah data dengan perilaku data yang memiliki varians yang tidak terlalu besar dan mempunyai kecenderungan untuk mendekati nilai rata ratanya test sesuai dengan yang menciptakan yaitu David Dickey dan Wayne Fuller. Adapun hipotesis dalam uji ini adalah:
Ho: terjadi unit root (Data tidak stasioner)
H1: tidak terjadi unit root (Data stasioner)
Tabel 3
Output Uji ADF PDRB Bali
|
t-Statistik |
Prob.* | |
|
Augmented Dickey-Fuller test statistik |
-1.153137 |
0.9038 |
|
Test critical values: 1% level |
-4.262735 | |
|
5% level |
-3.552973 | |
|
10% level |
-3.209642 |
Berdasarkan hasil ouput di atas, nilai Prob. adalah sebesar 0,9038 (nilai ini lebih besar dari nilai alfa 0,05). Dari hasil tersebut dapat
Tabel 2
Output Correologram PDRB Bali
|
Autocorrelation |
Partial Correlation |
AC PAC |
Q-Stat |
Prob |
|
I AAAAAAA |
j AAAAAAA |
1 0.915 0.915 |
34.360 |
0.000 |
|
I AAAAAA I |
■ I ■ |
2 0.841 0.030 |
64.245 |
0.000 |
|
J AAAAAA j |
I ■ |
3 0.762 -0.069 |
89.491 |
0.000 |
|
J AAAAA J |
■* I ■ |
4 0.666 -0.157 |
109.32 |
0.000 |
|
J AAAA j |
• I ■ |
5 0.586 0.033 |
125.16 |
0.000 |
|
J AAAA j |
■ I ■ |
6 0.518 0.037 |
137.89 |
0.000 |
|
I AAA |
■ I ■ |
7 0.449 -0.028 |
147.78 |
0.000 |
|
J AAA |
∙* I ■ |
8 0.381 -0.071 |
155.14 |
0.000 |
|
J AA |
I ■ |
9 0.310 -0.081 |
160.16 |
0.000 |
|
J AA |
■ I ■ |
10 0.243 -0.016 |
163.36 |
0.000 |
|
• I *∙ |
■ I ■ |
11 0.179 -0.018 |
165.16 |
0.000 |
|
■ I ■ |
12 0.116 -0.046 |
165.95 |
0.000 | |
|
■ |
13 0.051 -0.083 |
166.10 |
0.000 | |
|
■ I ■ |
14 -0.010 -0.045 |
166.11 |
0.000 | |
|
■ I ■ |
15 -0.063 0.001 |
166.37 |
0.000 | |
|
I ■ |
• I ■ |
16 -0.115 -0.039 |
167.29 |
0.000 |
disimpulkan bahwa terima Ho atau data PDRB Bali tidak stasioner.
Merubah Data Time Series yang Non Stasioner menjadi Stasioner
Analisis time series mengharuskan data bersifat stasioner. Dalam hal ini, data PDRB
Bali bersifat tidak stasioner, oleh karena itu perlu di diferensiasi agar menjadi stasioner. Proses diferensiasi yang dilakukan adalah dengan mengurangkan PDRB t dengan PDRB t-1 (first difference).
Dari grafik di bawah ini terlihat bahwa pola PDRB t-1 (first difference) sudah tidak membentuk pola tertentu sehingga dapat disimpulkan bahwa PDRB t-1 (first difference) sudah stasioner pada
Selain dari grafik yang sudah menunjukkan bahwa data PDRB stasioner, uji akar unit pun menunjukkan hasil yang sama. Berdasarkan hasil ouput di bawah ini, nilai Prob. menunjukkan nilai sebesar 0,000 (nilai ini lebih kecil dari nilai alfa 0,05). Dari nilai tersbut dapat disimpulkan bahwa hasil pengujian adalah tolak Ho atau data PDRB stasioner.
level 1.
Grafik 3.
Perkembangan PDRB Bali Triwulan I 2007 – Triwulan II 2016 (setelah proses diferensiasi)
PDRB_1
3,000,000
2,000,000
1,000,000
-1,000,000
-2,000,000
-3,000,000
0

Identifikasi ARIMA (Penentuan Ordo AR, MA)
Langkah selanjutnya adalah mengidentifikasi model ARIMA yang akan digunakan untuk meramalkan data PDRB ke depan nya. Identifikasi model ARIMA berkaitan dengan penentuan ordo (p,d,q) dimana p ditentukan dari nilai PAC; q ditentukan dari nilai AC; dan d adalah level dimana data stasioner. Dalam hal ini nilai d adalah 1, karena data PDRB stasioner pada diferensiasi pertama. Untuk mendeteksi apakah data PDRB mengikuti pola AR atau MA atau ARIMA digunakan Tabel di bawah ini.
Salah satu cara lain yang dapat digunakan untuk menentukan ordo AR, MA adalah dengan
Tabel 5. Correologram pada 1 st difference
|
Autocorrelation |
Partial Correlation |
AC |
PAC |
Q-Stat |
E⅛κfe | |
|
*i∣. I |
*i∣. I |
1 |
-0.266 |
-0.266 |
2.8425 |
0.092 |
|
■’l ■ I |
”1 ■ I |
2 |
-0.159 |
-0.248 |
3.8876 |
0.143 |
|
”1 ■ I |
*** I |
3 |
-0.217 |
-0.385 |
5.8873 |
0.117 |
|
I ** I |
■ I ■ I |
4 |
0.263 |
0.011 |
8.9205 |
0.063 |
|
■ I ■ I |
5 |
0.011 |
-0.022 |
8.9255 |
0.112 | |
|
■’1 ■ I |
■’1 ■ I |
6 |
-0.130 |
-0.155 |
9.7090 |
0.137 |
|
■’1 ■ I |
■’1 ■ I |
7 |
-0.070 |
-0.097 |
9.9414 |
0.192 |
|
I * |
■ I ■ I |
8 |
0.185 |
0.072 |
11.651 |
0.167 |
|
■ I ■ I |
■ I* I |
9 |
0.072 |
0.093 |
11.920 |
0.218 |
|
■’I ■ I |
■ I ■ I |
10 |
-0.111 |
0.026 |
12.581 |
0.248 |
|
■’1 ■ I |
■ I ■ I |
11 |
-0.128 |
-0.043 |
13.486 |
0.263 |
|
I * |
■ I ■ I |
12 |
0.140 |
0.067 |
14.609 |
0.264 |
|
I * |
■ I* I |
13 |
0.170 |
0.198 |
16.346 |
0.231 |
|
■ I ■ I |
14 |
-0.177 |
-0.020 |
18.316 |
0.193 | |
|
■’1 ■ I |
■ I ■ I |
15 |
-0.114 |
-0.034 |
19.173 |
0.206 |
|
I * |
■ I ■ I |
16 |
0.102 |
0.059 |
19.894 |
0.225 |
|
I * |
■ I* I |
17 |
0.195 |
0.122 |
22.642 |
0.161 |
|
*i∣. I |
■M . I |
18 |
-0.211 |
-0.112 |
26.022 |
0.099 |
|
■ I ■ I |
■ I ■ I |
19 |
-0.062 |
-0.022 |
26.328 |
0.121 |
|
■ I ■ I |
20 |
0.070 |
0.022 |
26.741 |
0.143 | |
Tabel 3
Output Uji ADF PDRB Bali
|
t-Statistik |
Prob.* | |
|
Augmented Dickey-Fuller test statistik |
-12.65294 |
0.0000 |
|
Test critical values: 1% level |
-4.252879 | |
|
5% level |
-3.548490 | |
|
10% level |
-3.207094 |
melihat nilai PAC dan AC nya. Dari nilai PAC dan AC tersebut dibandingkan dengan nilai t 1.96 [-Jl) (Chaido Dritsaki, 2015) . Jika nilai AC atau PAC di suatu lag berada dalam rentang besaran tersebut maka data stasioner, dan itulah ordo dari model ARIMA yang akan digunakan. Dari data PDRB, rentang nilai t 1.96 Js J adalah -0,3795 s.d 0,3795.
Dari nilai AC diatas, maka keseluruhan nilai AC berada pada rentang nilai tersebut. Hal itu menandakan bahwa ordo untuk MA adalah 0. Sedangkan nilai PAC digunakan untuk mencari nilai ordo dari AR. Nilai PAC yang berada di luar range di atas adalah pada lag ke 3, hal ini menyimpulkan bahwa ordo AR adalah 3. Jadi model ARIMA yang terbentuk adalah ARIMA (3,1,0).
Uji Diagnostik Model ARIMA
Setelah mendapatkan model untuk data
PDRB, langkah selanjutnya adalah dengan menguji apakah model yang didapat akan dapat meramalkan data PDRB ke depan dengan baik. Uji diagnostic ini salah satu uji yang dapat digunakan untuk menguji kecocokan model dalam peramalan ke depan. Berdasarkan tabel di bawah ini didapatkan nilai Prob. untuk kesemua coefficient dalam model adalah 0 (lebih kecil dari alfa 0,05 persen). Dari hal tersebut dapat disimpulkan bahwa model yang ARIMA yang didapat adalah Model ARIMA yang cocok untuk meramal angka PDRB di masa depan. Peramalan PDRB Triwulanan Provinsi Bali dengan ARIMA
Adapun model ramalan PDRB triwulanan Provinsi Bali dengan model ARIMA (3,1,0) adalah sebagai berikut:
ΔYt= 433037,3 - 0,524858 ΔYt, - 0,515134 ΔYt2-0,447398 ΔYt-3
Tabel 6
Output ARIMA (3,1,0)
|
Variable |
Coefficient |
Std. Error |
t-Sta tistik |
Prob. |
|
C |
433037.3 |
28176.00 |
15.36901 |
0.0000 |
|
AR(I) |
-0.524858 |
0.086216 |
-6.087718 |
0.0000 |
|
AR(2) |
-0.515134 |
0.089090 |
-5.782147 |
0.0000 |
|
AR(B) |
-0.447398 |
0.086442 |
-5.175724 |
0.0000 |
|
Rsquared |
0.671801 |
Mean dependent var |
499880.4 | |
|
Adjusted R-squared |
0.638981 |
S.D. dependent var |
674943.0 | |
|
S.E. of regression |
405538.6 |
Akaike info criterion |
28.77395 | |
|
Sum squared resid |
4.93E+12 |
Schwarz criterion |
28.95352 | |
|
Log likelihood |
-485.1572 |
Hannan-Quinn criter. |
28.83519 | |
|
F-Statistik |
20.46930 |
Durbin-Watson stat |
1.638460 | |
|
Prob (F-sta tistik) |
0.000000 |
Tabel 7
Proyeksi PDRB Triwulanan Provinsi Bali dengan Model ARIMA (3,1,0) dengan Skenario Pisimis, Moderat, dan Optimis (dalam juta rupiah)
|
Tiiwulan |
E⅛≡sui≡ |
Mssissi |
Optimis |
|
2016; 3 |
35.041.833 |
36.886.140 |
38.730.447 |
|
2017; 1 |
35.453.221 |
37.319.180 |
39.185.139 |
|
2017; 2 |
35.864.609 |
37.752.220 |
39.639.831 |
|
2017; 3 |
36.275.988 |
38.185.250 |
40.094.513 |
|
2017; 4 |
36.687.378 |
38.618.290 |
40.549.205 |
|
2018; 1 |
37.098.764 |
39.051.330 |
41.003.897 |
|
2018; 2 |
37.510.142 |
39.484.360 |
41.458.578 |
|
2018; 3 |
37.921.530 |
39.917.400 |
41.913.270 |
|
2018; 4 |
38.332.918 |
40.350.440 |
42.367.962 |
Dimana adalah perubahan dari PDRB. Untuk memperoleh proyeksi dari PDRB maka perubahan PDRB pada tahun ke-t ditambahkan dengan PDRB tahun sebelumnya. Dari model tersebut maka diperoleh PDRB hasil peramalan dengan model ARIMA (3,1,0) yang dapat dilihat pada tabel 7. Ramalan moderat diperoleh dengan menggunakan eviews. Sedangkan ramalan pesimis dan optimis diperoleh dari batas bawah dan batas atas pada derajat kepercayaan 95 persen.
Berdasarkan Tabel 7 dapat dilihat hasil peramalan PDRB Bali triwulan II 2016 sampai dengan triwulan IV 2018 menggunakan model ARIMA (3,1,0). Dari tabel tersebut diketahui bahwa Total PDRB Bali yang tercipta di triwulan III tahun 2016 ini adalah sebesar 36,89 triliun rupiah. Sedangkan PDRB Bali akan meningkat 9,39 persen di triwulan IV tahun 2018. Meramal tidak hanya berbicara masa depan, tapi bagaimanakah ketepatan model tersebut jika digunakan untuk peramalan data yang telah di publish sebelumnya. Grafik 4 menggambarkan hal tersebut.
Grafik 4
Perbandingan PDRB Hasil Penghitungan dengan PDRB Hasil Estimasi dengan Model ARIMA (3,1,0)
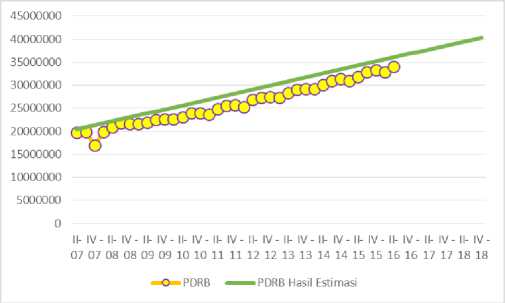
Dari grafik 4 di atas dapat dilihat keselarasan antara PDRB yang sudah di release dengan PDRB hasil ramalan dengan metode ARIMA dari triwulan II 2007 sampai triwulan IV 2018. Adapun rata rata selisih diantara keduanya adalah sebesar 8,76 persen.
KESIMPULAN DAN SARAN
Kesimpulan
Model ARIMA terbaik yang mampu menggambarkan PDRB Triwulanan Bali dari triwulan I 2007 sampai dengan triwulan II 2016 adalah ARIMA (3,1,0). Adapun hasil ramalan PDRB Bali dari triwulan I 2007 sampai triwulan II 2016 memiliki rata rata perbedaan 8,76 persen dengan PDRB yang sudah di release oleh BPS
Provinsi Bali.
Adapun ramalan PDRB Bali di triwulan III 2016 adalah sebesar Rp. 36.886.140 dengan laju pertumbuhan sebesar 7,24 persen (jika dibandingkan dengan PDRB hasil release triwulan sebelumnya).
Saran
Agar ranah penelitian semakin kaya, maka bagi peneliti selanjutnya bisa membuat ramalan PDRB dengan metode lainnya selain metode ARIMA.
REFERENSI
Andrei, Adriana. Econometric Modeliing of GDP Time series. Theoretical and Applied Economics Volume XVIII (2011), No. 10(563), pp. 91-98. E-journal. University of Bucharest
Bopulas, Brenda. 2011. Forecast Model of the Gross Domestic Product: an application of Box-Jenkins methodology. Universiti Malaysia Sarawak.
BPS Provinsi Bali. 2015. Produk Domestik Regional Bruto Provinsi Bali, Tahun 2011 – 2015.
Dritsaki, Chaido. 2015. Forecasting Real GDP Rate through Econometric Models: An Empirical Study from Greece. Journal of International Business and Economics June 2015, Vol. 3, No. 1, pp. 13-19. E-journal. American Research Institute for Policy Development
Maity, Bipasha. 2012. Forecasting GDP Growth Rates of India: An Empirical Study. International Journal of Economics and Management Sciences Vol. 1, No.9, 2012, pp 52 -58. E-journal. Indian Institute of Technology.
Rahardja, Pratama dan Mandala Manurung, 2001. Teori Ekonomi Makro: Suatu Pengantar. Jakarta: LP FE Universitas Indonesia.
Sukirno, Sadono. 2006. Ekonomi Pembangunan. Jakarta : Kencana Group
Utama, Made Suyana. 2014. Model Box Jenkins
Dalam Rangka Peramalan Produksi Domestik Regional Bruto Propinsi Bali. Jurnal Buletin Studi Ekonomi Vol 19, No. 1. E-journal. Universitas Udayana.
Widarjono, Agus. 2013. Ekonometrika: Pengantar dan Aplikasinya Disertai Panduan Eviews. Yogyakarta: UPP STIM YKPM
72
Discussion and feedback