Model ARIMAX Dan Deteksi GARCH Untuk Peramalan Inflasi Kota Denpasar Tahun 2014
on
JEKT ♦ 7 [2] : 168 - 182
ISSN : 2301 - 8968
Model ARIMAX Dan Deteksi GARCH
Untuk Peramalan Inflasi Kota Denpasar Tahun 2014
Rukini*)
Badan Pusat Statistik Provinsi Bali
ABSTRAK
Inflasi merupakan indikator penting yang dapat memberikan informasi mengenai perkembangan harga barang dan jasa yang dikonsumsi masyarakat. Peramalan terhadap inflasi menjadi penting agar dapat membantu pemerintah dalam mengambil kebijakan untuk menjaga stabilitas moneter di masa yang akan datang. Secara umum peramalan inflasi dapat dilakukan dengan pendekatan time series, pendekatan kausal, dan gabungan antara pendekatan time series dan kausal. Model dengan pendekatan gabungan yang banyak digunakan untuk peramalan inflasi adalah ARIMAX yang mencakup model Fungsi Transfer dan Model Intervensi atau dikenal juga dengan model regresi dinamis. Selain itu, pendekatan Generalized Autoregresive Conditional Heteroscedasticity (GARCH) untuk model varians juga telah diaplikasikan pada peramalan inflasi. Dalam Penelitian ini akan dijelaskan prosedur pembentukan model ARIMAX dan deteksi GARCH sebagai studi kasus digunakan data inflasi Kota Denpasar. Variabel prediktor yang digunakan terdiri atas variabel data metrik (yaitu jumlah wisatawan mancanegara) dan variabel data non metrik (yaitu kenaikan bahan bakar minyak (BBM), tarif dasar listrik (TDL), dan kejadian bom Bali). Model terbaik untuk data in-sample adalah model intervensi dengan nilai AIC dan SBC terkecil, sedangkan untuk data out-sample model terbaiknya adalah model fungsi transfer dengan nilai RMSE terkecil. Hasil deteksi GARCH dengan uji Lagrange Multiplier menunjukkan tidak ditemukan adanya unsur heteroskedastisitas pada model ARIMAX.
Kata kunci: ARIMAX, GARCH, ⅰпflаѕⅰ, metrik, non metrik
ARIMAX Model And GARCH Detection For Forecasting Inflation In Denpasar 2014
ABSTRACT
Inflation is an important indicator that can provide information on the development of prices of goods and services consumed by public. Forecasting inflation is important in order to assist the government in taking monetary policy to maintain economic stability in the future. In general, forecasting inflation can be done with time series approach, causal approach, and a combination of time series and causal approaches. Models with a combined approach that is widely used for forecasting inflation is ARIMAX model that includes Transfer Function and Intervention Model or also known as dynamic regression models. In addition, Generalized Autoregresive Conditional Heteroscedasticity (GARCH) for variance has also been applied to models in forecasting inflation. This study explains the procedure of building the ARIMAX models and GARCH detection using a case study of inflation data in denpasar city. Predictor variables consist of metric data variable (ie number of foreign tourists) and non-metric data variables (the increase of fuel oil (BBM) ), basic electricity tariff (TDL) and Bali bombings). The best model for in-sample data is intervention model with the smallest value of AIC and SBC, whereas the best model for data out-sample is transfer function model with the smallest RMSE value. GARCH detection results with Langrange Multiplier test shows no evidence of heteroscedasticity in ARIMAX model.
Keywords: ARIMAX, GARCH, ⅰпflation, metric, non-metric.
PENDAHULUAN
Inflasi dapat diartikan juga sebagai suatu proses meningkatnya harga barang dan jasa secara umum, terus menerus dan saling mempengaruhi. Penyebab inflasi dapat dikelompokkan menjadi tiga kategori, yaitu Ekspektasi Inflasi, Volatilitas Nilai Tukar dan Output Gap yang berupa ketidakseimbangan antara permintaan dan pasokan (Hasbullah, 2012). Ekspektasi inflasi biasanya disebabkan oleh kenaikan tarif dasar listrik (TDL), bahan bakar minyak (BBM), elpiji dan lain-lain. Inflasi memiliki dampak positif dan negatif tergantung pada besar kecilnya tingkat inflasi. Karena besarnya pengaruh yang ditimbulkan inflasi terhadap perekonomian negara, maka perlu dilakukan peramalan terhadap tingkat inflasi pada masa yang akan datang guna menentukan langkah-langkah yang harus disiapkan dalam menghadapi kondisi ekonomi ke depan yang dipengaruhi oleh inflasi. Peramalan inflasi berhubungan dengan peramalan data runtun waktu atau time series. Model time series yang paling populer dan banyak digunakan dalam peramalan data time series univariat adalah model Autoregressive Integrated Moving Average atau yang dikenal dengan model ARIMA (Makridakis et al., 1998). Prosedur Box-Jenkins merupakan prosedur baku (standar) yang dikenalkan oleh Box-Jenkins (1976) untuk mendapatkan model ARIMA yang sesuai pada suatu data runtun waktu.
Penelitian-penelitian sebelumnya mengenai peramalan inflasi yang menggunakan teknis model time series multivariate diantaranya dilakukan oleh Kismiantini dan Dhoriva (2010) dampak penurunan harga BBM jenis premium terhadap angka inflasi di Kota Yogyakarta menggunakan model intervensi dengan step function dan Rokimah (2012) yang meramalkan inflasi Jawa Timur dengan pendekatan fungsi transfer dan artificial neural network. Sampai hari ini sejauh penulis ketahui belum ada penelitian yang melibatkan gabungan input metrik (yaitu jumlah wisatawan mancanegara ) dan non metrik (yaitu kenaikan bahan bakar minyak (BBM), tarif dasar listrik (TDL) dan kejadian bom Bali), khususnya yang menjelaskan prosedur pembentukan modelnya. Metode pendekatan gabungan yang banyak digunakan dalam peramalan inflasi adalah ARIMAX yang mencakup model fungsi transfer dan model intervensi. Sebagai salah satu metode dalam analisis data time series, ARIMA dan ARIMAX menjadi metode yang dipakai secara luas dalam ekonometrika. Metode ini mensyaratkan beberapa kondisi yang harus dipenuhi, antara lain data harus stasioner, baik stasioner dalam mean ataupun stasioner dalam varians. Selain itu,
residual dari model tersebut harus bersifat white noise yaitu residual mempunyai mean nol dan mempunyai varians yang konstan (Box dan Jenkins, 1976).
Dalam praktek, pemodelan ARIMA atau ARIMAX pada suatu data ekonomi seringkali memberikan residual d engan varians yang tidak konstan (heterogen). Engle (1982) memperkenalkan model Autoregressive Conditional Heteroscedasticity (ARCH) untuk memodelkan inflasi di Inggris yang mengandung varians yang tidak konstan. Kemudian model ARCH disempurnakan menjadi Generalized ARCH (GARCH) oleh Bolerslev (1986). Metode ini mampu mengatasi heteroskedastisitas dalam data deret waktu. Berdasarkan latar belakang yang telah diuraikan diatas, maka rumusan masalah dalam penelitian ini adalah: Bagaimana prosedur pembentukan model ARIMAX dengan prediktor (input) gabungan data metrik dan non metrik dan mengidentifikasi heteroskedastisitas untuk residual model ARIMAX dengan prediktor gabungan data metrik dan data non metrik serta berapa nilai ramalan inflasi Kota Denpasar bulan Januari-Desember 2014 berdasarkan model ARIMAX
Metode ARIMA Box-Jenkins
Prosedur pembentukan model ARIMA meliputi beberapa tahapan yaitu identifikasi, estimasi, cek diagnosa dan peramalan. Model Box-Jenkins (ARIMA) dibagi ke dalam 3 kelompok, yaitu: model autoregressive (AR), moving average (MA), dan model campuran ARMA (autoregressive moving average) yang mempunyai karakteristik dari dua model pertama.
-
1) Identifikasi
-
a. Bentuk model AR (p) atau model ARIMA (p ,0,0) secara umum adalah :
Zt = ΦZt-1 + Φ2 Zt-1 + ... + Φp Zt—p + at.................(1) φp (B) Zt = at
-
b. Bentuk model MA (q) atau model ARIMA (0,0, q) secara umum adalah:
Zt = at - θ1at-1 - θ2at-2 - ...θqat-q
Zt = θ (B)at
-
c. Bentuk model ARMA (p, q) atau model ARIMA (p, 0, q)) secara umum adalah:
Zt = Φzt-1 + Φ2 Zt-1 + ... + Φp Zt-p + at — θ1at-1 — θ2at-2 – ...θqat-q
-
d. Bentuk umum model ARIMA adalah :
φp (B) (1-B)d Zt = θo + θq (B)at(4)
Tabel 1. Karakteristik ACF dan PACF yang Stasioner
|
Proses |
ACF |
PACF |
|
Autoregressive orde p |
Dies down |
Cuts off setelah lag ke-p |
|
Moving Average orde q |
Cuts off setelah lag ke-q |
Dies down |
|
ARMA orde (p,q) |
Dies down |
Dies down |
-
e. Sedangkan gabungan antara model ARIMA non musiman dan ARIMA musiman disebut ARIMA multiplikatif yang dinyatakan sebagai berikut :
Φp(Bs)φp(1 – B)d 1 – Bs)DŻt = θq(B)ΘQ(Bs)at
......…..(5)
-
2) Estimasi Parameter
Ada beberapa cara yang dapat digunakan untuk mendapatkan parameter-parameter model ARIMA (Wei, 2006), antara lain: Metode Momen; Metode Maximum Likelihood, dan Metode OLS (Ordinary Least Squares). Secara umum, misalkan δ adalah suatu parameter pada model ARIMA (mencakup φ, θ, dan µ) dan δ adalah nilai estimasi dari parameter tersebut, serta s.e ( ) adalah standar error dari nilai taksiran maka uji signifikansi parameter dapat dilakukan sebagai berikut:
Hipotesa:
H0 : δ = 0 (parameter tidak signifikan)
H0 : δ ≠ 0(parameter signifikan)
Statistik uji:
t =
()
s.e( )
.......................................(6)
Daerah penolakan : Tolak H0 jika 111 > ta /2. n - m atau menggunakan nilai p-value < α artinya parameter signifikan.
-
3) Pemeriksaan Diagnostik
Pemeriksaan diagnosis residual dari model, yaitu residual bersifat white noise juga berdistribusi normal. Pengujian asumsi white noise menggunakan uji Ljung-Box dengan hipotesis sebagai berikut:
H0 ρ1 = ρ2 = ... = ρK = 0 (residual White Noise)
H1 : minimal ada satu ρk≠ o (residual tidak White
Noise),
dengan k = 1,2,..., K
Statistik Uji:
K
Q = n(n + 2)∑ (n - k)-1 Pk2.....................................(7)
k=1
daerah penolakan: Tolak H0 jika Q > χ2(α κ-m), dengan m = p + q (orde ARMA) atau dengan menggunakan p-value < α, artinya model tidak sesuai karena residual tidak memenuhi asumsi White
Noise. Pengujian selanjutnya yaitu uji asumsi residual berdistribusi normal. Pengujian ini dilakukan dengan menggunakan Kolmogorov Smirnov (Daniel, 1989). Hipotesis yang digunakan adalah :
H0 : Fn (x) = F0 (x) atau residual berdistribusi normal H1 : Fn (x) ≠ F0 (x) atau residual tidak berdistribusi normal
Statistik uji :
D = suP I Fn (x) - F0(x)l .................................(8)
x
Dimana, fungsi yang dihipotesiskan berdistribusi normal; Fn (x) = fungsi distribusi kumulatif dari data asal; dan n = banyaknya residual. Nilai Dhitung dibandingkan dengan nilai D pada tabel Kolmogorov-Smirnov dengan derajat bebas n . Daerah penolakan: Tolak H0 jika Dhitung > Da,n atau dapat menggunakan p-value. Jika p-value < α berarti H0 ditolak yang berarti residual tidak berdistribusi normal.
-
4) Pemilihan Model Terbaik
Untuk menentukan model terbaik dapat digunakan kriteria pemilihan model yang berdasarkan residual dan kesalahan peramalan (Wei, 2006). Adapun kriteria pemilihan model yang berdasarkan residual pada data in-sample menggunakan nilai AIC dan SBC. Sedangkan untuk pemilihan model berdasarkan kesalahan peramalan pada data out-sample menggunakan nilai RMSE
Model ARIMAX
-
1) Prosedur Pembentukan Model Fungsi Transfer
Bentuk umum model fungsi transfer untuk input tunggal (xt) dan output tunggal (yt) adalah (Wei, 2006):
y1 = v(B)x1 + nt
ωs(B) yt = s x1
δr(B)
θq(B) a φp(B) t
.................................(9)
Tahapan Pembentukan Model ARIMAX dengan Input Data Metrik (Model Fungsi Transfer) dijabarkan berikut ini.
-
a. Identifikasi bentuk model
-
(i) Mempersiapkan deret input dan deret output
-
(ii) Prewhitening deret input dan deret output diasumsikan deret input xt mengikuti proses ARMA :
fx(B)x1 = qx(B)at…………………..……………………(10)
dimana at adalah white noise. Deret at yaitu :
a t = fx(B)_ ............................................(11)
qx(B)xt
dan untuk deret bt adalah:
f (B)
b = x _ yt ……………………………(12)
t qx(B)
(iii)Penghitungan Crosscorrelation Function (CCF) dan autokorelasi untuk deret input dan deret output yang telah di-prewhitening.
rab(k) =
gab(k) _ sasb(B)
…………………………(13)
k = 0, ±1, ±2
(iv) Penaksiran bobot respon impuls
(v)Penetapan (b, r, s) untuk model fungsi transfer
berdasarkan plot CCF
(vi) Penaksiran awal deret gangguan (noise series)
n t = y t - v( B ) xt
w (B)
nt = yt--^_----Bbxt
tt t
(14)
(vii) Penentuan model ARIMA dari deret gangguan
nt
fp(B)nt =qq(B)at………………………………….(15)
-
b. Estimasi Parameter Model Fungsi Transfer c. Diagnosa Model Fungsi Transfer
-
2) Prosedur Pembentukan Model Intervensi
Bentuk umum dari model intervensi adalah dijabarkan pada Persamaan 16 berikut (Wei, 2006).
y = f jL Ij t + Jqq(BL at y ∑ d r f B fp(B)
……………..(16)
Tahapan Pembentukan Model ARIMAX dengan Input Data Non Metrik (Model Intervensi) dijabarkan berikut ini.
-
a. Identifikasi Bentuk Model
-
(i) Mempersiapkan data berdasarkan waktu-waktu intervensi
-
(ii) Menentukan model ARIMA menggunakan prosedur Box-Jenkins
-
(iii) Identifikasi order model intervensi (b, r, s)
Dalam mengidentifikasi order pada model intervensi, ada dua metode yang dapat dilakukan yaitu : 1) Metode Eksploratori dimana order (b, r, s) didapatkan melalui suatu besaran statistik untuk mengeksplorasi kemungkinan order (b, r, s) yang sesuai dengan melihat plot residual (Yt*); dan 2) Metode Konfirmatori, dimana order (b, r, s) ditetapkan berdasarkan diskriptif data melalui plot time series pada setiap waktu dimana terjadi intervensi tersebut.
-
b. Estimasi Parameter Model Intervensi c. Diagnosa Model Fungsi Intervensi
-
3) Prosedur Pembentukan Model ARIMAX Input Gabungan Data Metrik dan Non Metrik Tahapan Pembentukan Model ARIMAX Input Gabungan Data Metrik dan Non Metrik dijabarkan berikut ini.
-
a. Identifikasi Bentuk Model
Dalam identifikasi order model ARIMAX dengan input gabungan data metrik dan non metrik dapat dilakukan dengan dua kemungkinan: 1) Jika order (p, q) dari model fungsi transfer dan model intervensi sama maka tahapan estimasi dilakukan dengan (b, r, s) dari model fungsi transfer, (bi, r, si) dari model intervensi serta (p, q); dan 2) Jika order (p, q) dari model fungsi transfer dan model intervensi berbeda, maka pada tahap estimasi dicobakan untuk masing-masing model yaitu: (b, r, s) dari model fungsi transfer, (bi, ri, si) dari model intervensi serta (p, q) dari model fungsi transfer; dan (b, r, s) dari model fungsi transfer, (bi, ri, si) dari model intervensi serta (p, q) dari model intervensi.
-
b. Estimasi Parameter Model ARIMAX dengan input gabungan data metrik dan non metrik
-
c. Diagnosa Model ARIMAX dengan input gabungan data metrik dan non metric
DATA DAN METODOLOGI
Data yang digunakan dalam penelitian ini adalah data sekunder yaitu data inflasi Kota Denpasar, data tentang jumlah wisatawan mancanegara dan data tentang kejadian-kejadian khusus yang diduga menyebabkan kenaikan inflasi, yaitu kenaikan BBM, kenaikan TDL, dan kejadian Bom Bali I dan II. Data tersebut diamati mulai Januari 2000 sampai dengan Desember 2013. Pada proses analisis, data akan dibagi menjadi dua bagian yaitu data training untuk pembentukan model dan data testing untuk validasi dan pemilihan model terbaik. Data periode Januari 2000 sampai dengan Desember 2013 digunakan
Tabel 2. Deskripsi Tentang Variabel Penelitian
|
No |
Variabel |
Keterangan |
Skala | |
|
1 |
Yt |
Inflasi Kota Denpasar pada bulan ke-t |
Metrik (interval) | |
|
2 |
X1t |
Jumlah wisatawan mancanegara yang berkunjung ke Bali pada bulan ke-t Metrik (rasio) | ||
|
3 |
X2j,t |
Kejadian kenaikan BBM ke-j pada bulan ke-t |
Nonmetrik (nominal) | |
|
4 |
X3j,t |
Kejadian kenaikan TDL ke-j pada bulan ke-t |
Nonmetrik (nominal) | |
|
5 |
X4j,t |
Kejadian bom Bali ke-j pada bulan ke-t |
Nonmetrik (nominal) | |
|
Tabel 3. Deskripsi Tentang Variabel Kejadian Kenaikan BBM | ||||
|
Waktu (t) Intervensi % Kenaikan |
Tanggal Kejadian | |||
|
10 |
X21,t |
16,37% |
1Oktober 2000 | |
|
18 |
X22,t |
30,12% |
16 Juni 2001 | |
|
25 |
X23,t |
28,23% |
17 Januari 2002 | |
|
37 |
X24,t |
21% |
2 Januari 2003 | |
|
63 |
X25,t |
30% |
1 Maret 2005 | |
|
70 |
X26,t |
126% |
1 Oktober 2005 | |
|
101 |
X27,t |
28,73% |
24 Mei 2008 | |
|
162 |
X28,t |
44 % |
Juni 2013 | |
|
Tabel 4. Deskripsi Tentang Variabel Kejadian Kenaikan TDL | ||||
|
Waktu (t) Intervensi |
% Kenaikan |
Tanggal Kejadian | ||
|
37 |
X31,t |
6% |
Januari 2003 | |
|
40 |
X32,t |
6% |
April 2003 | |
|
43 |
X33,t |
6% |
Juli 2003 | |
|
46 |
X34,t |
6% |
Oktober 2003 | |
|
127 |
X35,t |
6% |
Juli 2010 | |
|
133 |
X36,t |
10% |
Januari 2011 | |
|
157 |
X37,t |
4 % |
Januari 2013 | |
|
160 |
X38,t |
4% |
April 2013 | |
|
163 |
X39,t |
4% |
Juli 2103 | |
|
166 |
X310,t |
4% |
Oktober 2013 | |
Tabel 5. Deskripsi Tentang Variabel Kejadian Bom Bali
Waktu (t) Intervensi Tanggal Kejadian
34 X41,t Oktober 2002
70 X42,t Oktober 2005
sebagai data training (in-sample) dan data periode Januari 2014 sampai dengan April 2014 sebagai data testing (out-sample).
Secara umum ada dua variabel yang digunakan dalam penelitian ini, yaitu variabel respon (output) dan variabel prediktor (input). Variabel output yang menjadi fokus kajian penelitian adalah inflasi bulanan di Kota Denpasar. Sedangkan variabel input penelitian terdiri atas variabel data metrik, yaitu jumlah wisatawan mancanegara yang berkunjung ke Bali, dan variabel data non metrik yaitu kejadian kenaikan BBM, kejadian kenaikan TDL, dan kejadian bom Bali. Semua variabel penelitian tersebut diamati dalam periode bulan.
Tahapan pengembangan prosedur untuk pemben-
tukan model ARIMAX terdiri dari prosedur pembentukan model dengan input data metrik (dikenal dengan model Fungsi Transfer) dan prosedur pembentukan model dengan input data nonmetrik (dikenal dengan model intervensi). Tahapan-tahapan yang akan dilakukan untuk pengembangan prosedur pembentukan model ARIMAX telah diuraikan sebelumnya. Model yang didapat kemudian dipilih berdasarkan kriteria model ARIMAX terbaik dan identifikasi homoskedas-tisitas varians dari semua model apakah mengandung unsur heteroskedastisitas. Langkah terakhir adalah menentukan nilai ramalan berdasarkan model terbaiknya.
HASIL DAN PEMBAHASAN
Pembentukan Model ARIMA untuk Data Inflasi Kota Denpasar
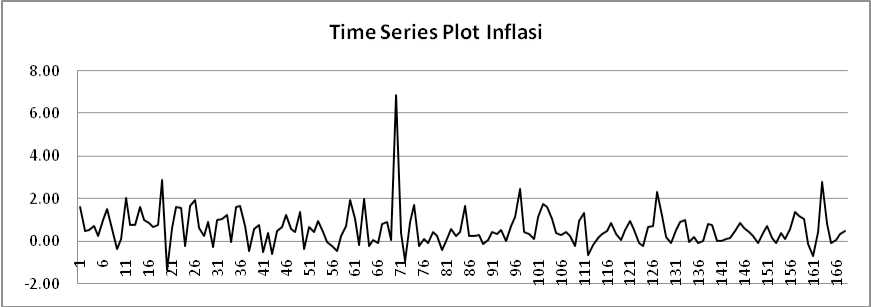
Plot time series dan plot ACF dari data inflasi Kota Denpasar akan digambarkan pada Gambar 1, 2, dan 3.
Gambar 1 Menunjukkan bahwa data sudah stasion-
Gambar 1. Time Series Plot Inflasi Kota Denpasar
Gambar 3. Plot PACF Inflasi Kota Denpasar
Gambar 2. Plot ACF Inflasi Kota Denpasar
|
Autocorrelation | |||
|
Lag |
-1 9 |
8 7 6 5 4 3 2 1 |
0 1 2 3 4 5 6 7 8 9 1 |
|
0 |
| |
|********************| | |
|
1 |
| |
. |
|* . | |
|
2 |
| |
**** |
| . | |
|
3 |
| |
. |
| . | |
|
4 |
| |
. |
|**. | |
|
5 |
| |
. * |
| . | |
|
6 |
| |
. |
| . | |
|
7 |
| |
. |
|*** | |
|
8 |
| |
. * |
| . | |
|
9 |
| |
.** |
| . | |
|
10 |
| |
. |
|* . | |
|
11 |
| |
. |
|* . | |
|
12 |
| |
. |
|* . | |
Lag 1 2 3 4 5 6 7 8 9 10 11 12
Partial Autocorrelations
-
-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
Tabel 6. Hasil Identifikasi Model ARIMA Inflasi Kota Denpasar
|
Model |
Signifikansi Parameter |
White Noise |
Berdistribusi Normal |
AIC |
SBC |
|
ARIMA (2,0,0) |
v |
v |
v |
328.9216 |
347.6653 |
|
ARIMA ([1,2],0,0) |
v |
v |
v |
323.4389 |
345.3067 |
|
ARIMA (0,0,2) |
v |
- |
Gambar 4. Time Series Plot Jumlah Wisman
er, namun ada satu titik ekstrim yang diduga dapat mempengaruhi pemodelan. Plot ACF pada Gambar 2 terlihat bahwa ada lag yang keluar dari batas signifikansi (lag ke-2 ada yang signifikan) artinya data belum white noise. Berdasarkan Plot ACF dan Plot PACF dugaan model ARIMA untuk data inflasi kota Denpasar seperti disajikan pada Tabel 6. Pada Tabel 6 menunjukkan bahwa model ARIMA yang sesuai untuk data inflasi Kota Denpasar adalah ARIMA ([1,2],0,0), dimana semua asumsi telah terpenuhi dan memiliki nilai AIC dan SBC terkecil.
Tahapan Pengembangan Prosedur Pembentukan model ARIMAX
-
1) Prosedur Pembentukan Model Fungsi Transfer (Input Data Metrik)
-
a. Identifikasi Bentuk Model
Proses identifikasi bentuk model akan dijabarkan melalui beberapa tahapan berikut.
-
(i) Mempersiapkan deret input dan deret output.
Deret input yang menjadi fokus pada penelitian ini
Time Series Plot Wisman
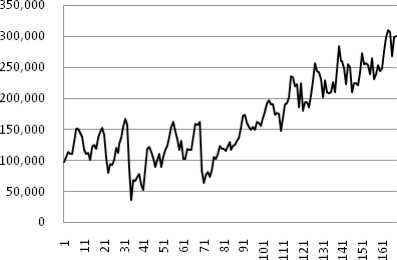
adalah jumlah wisatawan mancanegara (wisman)
Gambar 5 menunjukkan plot ACF jumlah wisatawan mancanegara, dimana terlihat pola dies down yang lambat dan berulang pada periode ke-12. Hal ini mengindikasikan bahwa data belum stasioner dalam mean (rata-rata) dan adanya faktor musiman. Sehing-
Gambar 5. Plot ACF Jumlah Wisman
Lag
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Autocorrelations
1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
Gambar 6. Plot ACF Jumlah Wisatawan Mancanegara Setelah Differencing 1 Regule dan Musiman 12
Autocorrelations
Lag 1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
0 | |********************|
ga perlu dilakukan differencing 1 reguler kemudian di differencing musiman 12.
Gambar 6 dan Gambar 7 menunjukkan plot ACF dan PACF data jumlah wisatawan mancanegara setelah differencing 1 reguler dan differencing musiman 12. Setelah dilakukan proses differencing, plot ACF memperlihatkan bahwa data telah stasioner dalam rata-rata. Melalui plot ACF dan PACF tersebut dapat diidentifikasi order model ARIMA yang sesuai untuk data jumlah wisatawan mancanegara. Dengan melihat pola PACF yang dies down dan ACF cut off di lag 12, maka dugaan model ARIMA yang terbentuk adalah model ARIMA (0,1,0)(0,1,1)12. Langkah selanjutnya adalah estimasi parameter dan diagnostik model deret input. Berdasarkan Tabel 7 menunjukkan bahwa dengan taraf signifikansi 5% parameter pada model ARIMA (0,1,0)(0,1,1)12 mempunyai nilai p-value kurang dari a = 0,05 maka H0 ditolak yang berarti bahwa parameter model ARIMA (0,1,0)(0,1,1)12
Gambar 7. Plot PACF Jumlah Wisatawan Mancanegara Setelah Differencing 1 Reguler Dan Musiman 12
Partial Autocorrelations
Lag -1 9 |
-
8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
***| . |
. *
.
. *
.
* .
.
.
* .
.
***
Tabel 7. Estimasi dan Uji Signifikansi Parameter Model ARIMA (0,1,0)(0,1,1)12 Jumlah Wisatawan Mancanegara
Parameter Estimasi p-value Keputusan
q12 0,67698 <0,0001 Signifikan
signifikan. Sehingga parameter dapat digunakan dalam model.
Berdasarkan Tabel 8 terlihat bahwa autokorelasi residual model ARIMA (0,1,0)(0,1,1)12 menunjukkan nilai p-value yang lebih besar dari a = 0,05 maka H0 diterima artinya autokorelasi residual tidak signifikan atau tidak terdapat korelasi antar lag atau residual sudah white noise. Oleh sebab itu model ARIMA (0,1,0)(0,1,1)12 layak digunakan dengan Persamaan (17) berikut.
(1 - B)(1 - B)12 x1t = (1 - Θ12 B12)at
(1 - B)(1 - B)12 x1t = (1 - 0,67698B12)at ......(17)
-
(ii) Pemutihan deret input dan pemutihan deret output
Setelah didapatkan model ARIMA (0,1,0)(0,1,1)12 maka pemutihan deret input dan deret output dapat ditentukan yaitu dari Persamaan (18) diperoleh persamaan deret input berikut.
a t = (1 - B )(1 - B12) Xt (1 - 0,67698B12)
b t = (1 - B )(1 - B12) yt (1 - 0,67698B12)
(18)
(19)
Langkah selanjutnya setelah pemutihan deret input dan deret output adalah pengecekan korelasi silang antar deret input dan deret output yang telah diputihkan.
-
(iii) Penghitungan korelasi silang antar deret input dan deret output yang telah diputihkan.
Tabel 8. Hasil Uji White Noise Residual Model ARIMA(0,1,0)(0,1,1)12 Jumlah Wisatawan Mancanegara
|
Lag |
Chi-Sqrt DF p-value Keputusan |
|
6 12 18 24 |
4,33 5 0,5023 White Noise 7,05 11 0,7950 White Noise 8,65 17 0,9507 White Noise 10,48 23 0,9879 White Noise |
Gambar. 8 Plot ACF Dari Deret Noise
|
Autocorrelation Plot of |
Residuals | |
|
Lag |
Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 |
3 4 5 6 7 8 9 1 Std Error |
|
0 |
2.680499 1.00000 | |***** |
***************| 0 |
|
1 |
-0.974651 -.36361 | *******| . |
| 0.080322 |
|
2 |
-0.737619 -.27518 | ******| . |
| 0.090319 |
|
3 |
0.247094 0.09218 | . |** . |
| 0.095575 |
|
4 |
0.558381 0.20831 | . |**** |
| 0.096147 |
|
5 |
-0.599711 -.22373 | ****| . |
| 0.099016 |
|
6 |
-0.187429 -.06992 | . *| . |
| 0.102226 |
|
7 |
0.712285 0.26573 | . |***** |
| 0.102534 |
|
8 |
-0.276189 -.10304 | . **| . |
| 0.106884 |
|
9 |
-0.419819 -.15662 | .***| . |
| 0.107523 |
|
10 |
0.530894 0.19806 | . |**** |
| 0.108985 |
|
11 |
0.553794 0.20660 | . |**** |
| 0.111283 |
|
12 |
-1.266280 -.47240 | *********| . |
| 0.113731 |
Pada tahap ini penghitungan korelasi silang dan autokorelasi dilakukan pada masing-masing deret input dan deret output yang telah diputihkan. Tujuannya adalah untuk mengetahui apakah ada hubungan dari waktu ke waktu yang mempengaruhi deret tersebut. Dari hasil korelasi silang diharapkan akan diperoleh hasil dimana deret input tidak mempengaruhi deret output. Penentuan nilai (b, r, s) didasarkan pada hasil plot Crosscorrelation Function (CCF). Analisis korelasi silang antara deret input dan deret output yang telah diputihkan yaitu hanya signifikan pada lag 0 dan 1, sehingga diduga nilai b=0, r=0, dan s=1 yang digunakan untuk menentukan bobot fungsi transfer selanjutnya.
(iv)Penaksiran bobot fungsi transfer sementara Pada tahap ini untuk menghasilkan bobot fungsi transfer menggunakan hasil yang telah diperoleh dalam korelasi silang antara deret input dan deret output yang telah diputihkan seperti pada Persamaan (20).
V(B)x1, = (w0 — wιB)x1t .....................(20)
-
(v) Penaksiran awal deret gangguan nt
Tahap selanjutnya adalah menghitung taksiran awal komponen noise dari model fungsi transfer dengan menggunakan Persamaan (21) berikut.
nt = yt - v(B)x1t
nt = yt - (w 0 — w1B)χιt ......................(21)
-
(vi) Identifikasi bentuk model ARIMA untuk nt
Dengan melihat plot ACF pada deret noise pada Gambar 8, dimana plot ACF cut off di lag 1,2,7,12. Dengan mengestimasi dan uji signifikansi parameter dugaan MA (1,2,7,12). Maka dugaan model deret noise adalah ARIMA (0,1,[1,2])(0,1,1)12. Setelah model ARIMA untuk deret noise didapat maka model fungsi transfer terbentuk pada Persamaan (22).
yI = w 0 — w ιB)x1t + (1 — q 1B — qJB2*1-q 2“) a,
…………………….(22)
-
b. Estimasi parameter model fungsi transfer
Berdasarkan Tabel 9 dapat disimpulkan bahwa parameter model fungsi transfer telah signifikan dengan taraf signifikansi 5%, dimana memiliki nilai p-value lebih besar dari alpha 0,05. Persamaan model fungsi transfer yang terbentuk adalah seperti tertuang dalam Persamaan (23).
y, = -0,0000162x1t + 0,0000198x1, , ttt-1
+ (1 - 0,81474B - 0,20846B2 )(1 - 0,76412B12)at
.........(23)
-
c. Diagnosa Model Fungsi Transfer
Tabel 10 menunjukkan bahwa model fungsi transfer telah memenuhi asumsi white noise dimana dengan taraf signifikansi 5% memiliki nilai p-value lebih besar dari 0,05. Tabel 4.6 menunjukkan hasil uji normalitas terhadap residual model fungsi transfer, dimana dengan taraf signifikansi 5% memiliki nilai p-value yang lebih besar dari 0,05 yang berarti model fungsi transfer telah memenuhi asumsi berdistribusi normal.
Pada Gambar 4.9 menunjukkan bahwa inflasi Kota
Tabel 9. Hasil Estimasi dan Uji Signifikansi Parameter Model Fungsi Transfer
|
Parameter |
Estimasi |
p-value |
Lag |
Variabel |
Keputusan |
|
q1 |
0,81474 |
<,0001 |
1 |
yt |
Signifikan |
|
q2 |
0,20846 |
0,0270 |
2 |
yt |
Signifikan |
|
q12 |
0,76412 |
<,0001 |
12 |
yt |
Signifikan |
|
w1 |
-0,0000162 |
0,0017 |
0 |
x1t |
Signifikan |
|
w2 |
-0,0000198 |
0,0001 |
1 |
x1t |
Signifikan |
Tabel 10. Hasil Uji White Noise Model Fungsi Transfer
|
Lag |
Chi-Square |
DF |
p-value |
Keputusan |
|
6 |
3,06 |
3 |
0,3820 |
White Noise |
|
12 |
11,04 |
9 |
0,2730 |
White Noise |
|
18 |
13,33 |
15 |
0,5771 |
White Noise |
|
24 |
18,12 |
21 |
0,6414 |
White Noise |
|
30 |
25,96 |
27 |
0,5206 |
White Noise |
Tabel 11. Hasil Uji Normalitas Residual Model Fungsi Transfer
|
Test D_hitung p-value |
Keputusan |
|
Kolmogorov- 0,063668 0,1286 Smirnov |
Berdistribusi Normal |
Denpasar pada bulan ke-t dipengaruhi oleh jumlah wisatawan mancanegara pada bulan ke-t sebesar -0,0000162 dan dipengaruhi oleh jumlah wisatawan mancanegara pada bulan ke-(t-1) sebesar -0,0000198.
-
2) Prosedu r Pembentukan Model Intervensi (Input
Data Non Metrik)
Penetuan order (b, r, s) untuk masing-masing intervensi berdasarkan deskriptif data yaitu dengan melihat plot t^ime series pada setiap t dimana terjadi intervensi ter^sebut.
Pembentuk^an model AR^IMAX (sem^ ua I^nter^-vensi)
Hasil estimasi dan uji signifikansi parameter model Intervensi gabungan dari masing-masing kejadian intervensi dapat dilihat pada Tabel 12. Untuk kejadian bom Bali II pada bulan Oktober 2005 tidak terlihat, hal ini karena waktu kejadian yang bersamaan dengan waktu kejadian kenaikan BBM bulan Oktober 2005. Sehingga tidak dimasukkan ke dalam model. Hasil identifikasi ACF dan PACF dapat dilihat pada Gambar 15 dan Gambar 16.
Tabel 13 menunjukkan bahwa semua parameter signifikan, hal ini ditunjukkan dengan taraf signifikansi 5% memiliki nilai p-value kurang dari 0,05.
Sehingga model intervensi yang diperoleh dapat ditulis dalam Persamaa^ n 2 4.
Gambar 9. Besarnya Efek Yang Ditimbulkan Dari Jumlah Wisatawan Mancanegara Terhadap Inflasi Kota Denpasar
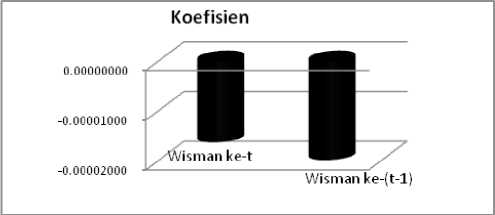
Gam bar 10. Time S^eries Plot I nflas i Kota Den pasar Saat Ke naika^n BBM Pad a t= 10, t=18, t=25 D an t= 37
10 18 25 37
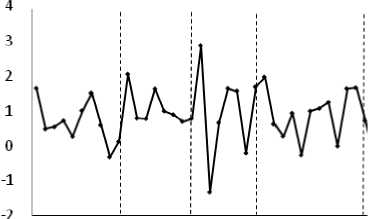
1 4 8 12 16 20 24 28 32 36 39
Gambar 11. Ti me Serie s Plot Infla si Kot a Den pasar Saat Ke n aika n BB M P a da t= 63, t=70 dan t=101
4

Gambar 12. Time Series Plot Inflasi Kota Denpasar Saat Kenaikan TDL Pad t=3 , t=40, t=43 dan t=46
Gambar 13. Time Series Plot Iitiflasi Kota Denpasar Saat K naika TDL Pada t=127 dan t=133
127 133
37 40 43 46
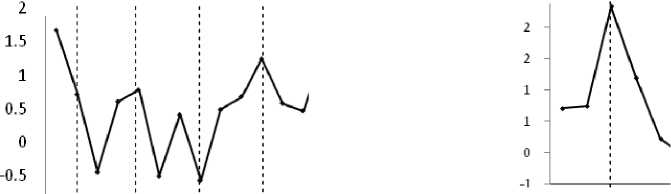
1 --------------:----------:----------■------- 126 129 132 135
^fi D 42 45 4S
Gambar 14. Time Series Plot Kejadian Bom Bali I dan II Pada t=34 dan t=70
34 70
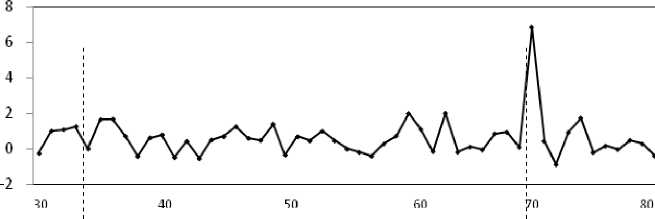
Bom Bali I (Oktober 2002)
Bom Bali II (Oktober 2005)
Tabel 12. Hasil Indentifikasi Order (b,r,s) Pada Masing-Masing Waktu Kejadian Intervensi
|
Intervensi |
Waktu (t) |
b |
r |
s |
Intervensi |
Waktu (t) |
b |
r |
s |
|
Kenaikan BBM |
10 |
1 |
0 |
0 |
Kenaikan TDL |
37 |
0 |
0 |
0 |
|
18 |
1 |
0 |
0 |
40 |
0 |
0 |
0 | ||
|
25 |
0 |
0 |
1 |
43 |
0 |
0 |
1 | ||
|
37 |
0 |
0 |
0 |
46 |
0 |
0 |
0 | ||
|
63 |
0 |
0 |
0 |
127 |
0 |
0 |
0 | ||
|
70 |
0 |
0 |
0 |
133 |
0 |
0 |
0 | ||
|
101 |
1 |
0 |
1 |
157 |
0 |
0 |
0 | ||
|
162 |
1 |
0 |
0 |
160 |
0 |
0 |
0 | ||
|
Bom Bali |
34 |
1 |
0 |
1 |
163 |
0 |
0 |
0 | |
|
70 |
0 |
0 |
0 |
166 |
0 |
0 |
0 |
Gambar 15. Plot ACF Residual Model Intervensi
Autocorrelation Plot of Residuals
|
Lag |
Covariance |
Correlation -1 9 8 |
7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 |
Std Error |
|
0 |
0.333696 |
1.00000 | |
|********************| |
0 |
|
1 |
0.044553 |
0.13351 | |
. |*** | |
0.077615 |
|
2 |
-0.060624 |
-.18167 | |
****| . | |
0.078986 |
|
3 |
-0.054939 |
-.16464 | |
***| . | |
0.081465 |
|
4 |
-0.0074751 |
-.02240 | |
. | . | |
0.083445 |
|
5 |
-0.033857 |
-.10146 | |
.**| . | |
0.083481 |
|
6 |
0.010161 |
0.03045 | |
. |* . | |
0.084221 |
|
7 |
0.044304 |
0.13277 | |
. |*** | |
0.084287 |
|
8 |
-0.0052827 |
-.01583 | |
. | . | |
0.085538 |
|
9 |
-0.010865 |
-.03256 | |
. *| . | |
0.085555 |
|
10 |
0.0069664 |
0.02088 | |
. | . | |
0.085630 |
Gambar 16. Plot PACF Residual Model Intervensi
|
Partial |
Autocorrelations | |
|
Lag |
Correlation -1 9 |
8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 |
|
1 |
0.13351 | |
. |*** | |
|
2 |
-0.20312 | |
****| . | |
|
3 |
-0.11505 | |
.**| . | |
|
4 |
-0.01936 | |
. | . | |
|
5 |
-0.15854 | |
***| . | |
|
6 |
0.04124 | |
. |* . | |
|
7 |
0.07857 | |
. |**. | |
|
8 |
-0.07865 | |
.**| . | |
|
9 |
0.03083 | |
. |* . | |
|
10 |
0.02490 | |
. | . | |
Tabel 13. Estimasi dan Uji Signifikansi Parameter Model Intervensi Dari Masing-Masing Kejadian yang Signifikan Terhadap Model
|
Parameter |
Estimasi |
p-value |
Lag |
variabel |
Shift |
Keputusan |
|
q0 |
0,46576 |
<,0001 |
0 |
Y |
0 |
Signifikan |
|
f1 |
0,20086 |
0,0166 |
1 |
Y |
0 |
Signifikan |
|
f12 |
-0,25989 |
0,0024 |
2 |
Y |
0 |
Signifikan |
|
w1 |
1,42137 |
0,0090 |
0 |
X21,t |
1 |
Signifikan |
|
w2 |
2,79271 |
<,0000 |
0 |
X22,t |
1 |
Signifikan |
|
w3 |
1,58623 |
0,0050 |
0 |
X23,t |
0 |
Signifikan |
|
w4 |
-1,27509 |
0,0225 |
0 |
X23,t |
0 |
Signifikan |
|
w5 |
1,85592 |
0,0007 |
0 |
X25,t |
0 |
Signifikan |
|
w6 |
6,23734 |
<,0001 |
0 |
X26,t |
0 |
Signifikan |
|
w7 |
1,22027 |
0,0295 |
0 |
X27,t |
1 |
Signifikan |
|
w8 |
-1,16094 |
0,0377 |
1 |
X27,t |
1 |
Signifikan |
|
w9 |
1,67564 |
0,0021 |
0 |
X35,t |
0 |
Signifikan |
|
w10 |
1,26131 |
0,0202 |
0 |
X41,t |
1 |
Signifikan |
|
w11 |
1,90163 |
0,0006 |
0 |
X28,t |
1 |
Signifikan |
Yt = 0,46576 -1,42137X21, t-1 - 2,79271X22, t-1 -1,5 8 6 23 X 23, t +1,27270 X 23, t
-1,85592X25,t - 6,23734X26t -1,22027X27,t +1,16094X27,t-1
-1,167564X3, -1,26131X4. t . -1,90163X2 ............................(24)
5 J 11-1 8 ti-1
+
at
(1 - 0,20086B + 0,25989B2)
Gambar 17.Besarnya Efek Yang Ditimbulkan Dari Semua Intervensi Yang Signifikan Terhadap Inflasi Kota Denpasar
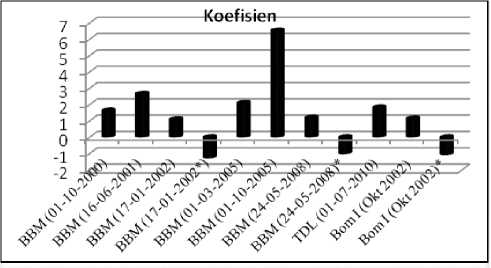
Berdasarkan Gambar 17 menunjukkan bahwa besarnya pengaruh yang ditimbulkan oleh semua intervensi yang signifikan terhadap inflasi Kota
Denpasar. Pengaruh terbesar yang ditimbulkan dari kenaikan harga BBM adalah pada bulan Oktober 2005 yaitu sebesar 6,23734 hal ini karena kenaikan harga BBM pada bulan Oktober 2005 sebesar 126%. Pengaruh yang ditimbulkan dari intervensi kenaikan TDL sebesar 1,67564, sedangkan pengaruh yang ditimbulkan karena kejadian bom Bali I sebesar 1,26131.
Tabel 14 menunjukkan hasil uji white noise residual, dapat disimpulkan bahwa residual pada model intervensi Inflasi Kota Denpasar berdasarkan semua kejadian intervensi telah memenuhi asumsi white noise. Pada uji normalitas residual model juga telah memenuhi asumsi berdistribusi normal. Dengan taraf signifikan 5% memiliki nilai p-value sebesar 0,1500 yang lebih besar dari 0,05 seperti terlihat pada Tabel 15.
-
3) Pembentukan model ARIMAX dengan input gabungan data metrik dan nonmetrik.
Tabel 14. Hasil Uji White Noise Residual Model Intervensi
|
Lag |
Chi-Square |
DF |
p-value |
Keputusan |
|
6 |
5,54 |
4 |
0,2362 |
White Noise |
|
12 |
9,68 |
10 |
0,4694 |
White Noise |
|
18 |
14,27 |
16 |
0,5789 |
White Noise |
|
24 |
16,69 |
22 |
0,7804 |
White Noise |
|
30 |
21,71 |
28 |
0,7947 |
White Noise |
|
Tabel 15. Hasil Uji Normalitas Residual Model Intervensi | ||||
|
Test |
D_hitung |
p-value |
Keputusan | |
|
Kolmogorov-Smirnov |
0,044789 |
0,1500 |
Berdistribusi Normal | |
Tabel 16. Estimasi dan Uji Signifikansi Parameter Model ARIMAX Dengan Input Gabungan Data Metrik dan Non Metrik Yang Telah Dikeluarkan Variabel Data Non Metrik Yang Tidak Signifikan
|
Parameter |
Estimasi |
p-value |
Lag |
variabel Shift |
Keputusan |
|
q0 |
0,77837 |
<,0001 |
1 |
Y0 |
Signifikan |
|
f1 |
0,47697 |
<,,0001 |
2 |
Y0 |
Signifikan |
|
f12 |
0,69847 |
<,0001 |
12 |
Y0 |
Signifikan |
|
w1 |
4,59041E-6 |
0,0644 |
0 |
X1t 0 |
Signifikan |
|
w2 |
2,21040 |
<,0001 |
0 |
X22,t 1 |
Signifikan |
|
w3 |
1,05282 |
0,0499 |
0 |
X23,t 0 |
Signifikan |
|
w4 |
1,68185 |
0,0017 |
0 |
X25,t 0 |
Signifikan |
|
w5 |
6,71510 |
<,0001 |
0 |
X26,t 0 |
Signifikan |
|
w6 |
1,34984 |
0,0178 |
0 |
X27,t 1 |
Signifikan |
|
w7 |
-1,33521 |
0,0190 |
1 |
X27,t 1 |
Signifikan |
|
w8 |
-1,48901 |
0,0061 |
0 |
X33,t 0 |
Signifikan |
|
w9 |
1,74742 |
0,0013 |
0 |
X35,t 0 |
Signifikan |
|
w10 |
0,96184 |
0,0820 |
0 |
X41,t 1 |
Signifikan |
|
w11 |
1,74865 |
0,0033 |
0 |
X2 ,t 1 |
Signifikan |
|
Tabel 17. Hasil Uji White Noise Residual Model ARIMAX Dengan Input Gabungan Data Metrik Dan Non Metrik | |||||
|
Lag |
Chi-Square |
DF |
p-value |
Keputusan | |
|
6 |
1,46 |
3 |
0,6920 |
White Noise | |
|
12 |
8,42 |
9 |
0,4927 |
White Noise | |
|
18 |
12,77 |
15 |
0,6203 |
White Noise | |
|
24 |
15,53 |
21 |
0,7952 |
White Noise | |
|
30 |
22,53 |
27 |
0,7102 |
White Noise | |
Hasil penelitian yang diperoleh menunjukkan bahwa order (p,q) dari model fungsi transfer dengan order (p,q) dari model intervensi berbeda, sehingga dicobakan untuk masing-masing model.
-
a. Pembentukan model ARIMAX dengan input gabungan data metrik dan non metrik berdasarkan model fungsi transfer.
Hasil Estimasi dan Uji Signifikansi Parameter Model ARIMAX dengan input gabungan data metrik dan non metrik setelah dikeluarkan variabel data non metrik yang tidak signifikan terlihat pada Tabel 4.12. Dengan menggunakan taraf signifikansi 10 % semua parameter signifikan dimana nilai p-value di bawah 0,1
Tabel 16 menunjukkan hasil uji white noise residual model ARIMAX dengan input gabungan data metrik
dan non metrik. Dengan taraf signifikansi 5 % semua lag telah memenuhi asumsi white noise, dimana memiliki nilai p-value lebih besar dari 0,05.
Sehingga model yang diperoleh dapat ditulis dalam Persamaan (25) berikut.
Yt =-0,0000045X1t - 2,2140X22,t -1,05282X23,t
-
-1,68185X25,t - 6,71510X26,t -1,34984X27,t
+1,33521X27,t-1 +1,48901X33,t -1,74 7 42X35,t
-
- 0,96184X4., l -1,74865X2.t l 1 ,t-1 8, t-1
+ (1 - 0,77837B - 0,47697B2 )(1 - 0,69847B12)at
…………………….(25)
Pengujian asumsi kenormalan dengan uji Kolmogorov-Smirnov dengan taraf signifikansi 5 % memiliki nilai p-value lebih besar dari 0,05. Sehingga
Tabel 18.Hasil Uji Normalitas Residual Model ARIMAX Dengan Input Gabungan Data Metrik Dan Non Metrik
|
Test |
D_hitung |
p-value |
Keputusan |
|
Kolmogorov-Smirnov |
0,063657 |
0,1317 |
Berdistribusi Normal |
Tabel 19. Estimasi dan Uji Signifikansi Parameter Model ARIMAX Dengan Input Gabungan Data Metrik dan Non Metrik Yang Telah Dikeluarkan Variabel Data Non Metrik Yang Tidak Signifikan
|
Parameter |
Estimasi |
p-value |
Lag |
variabel |
Shift |
Keputusan |
|
f1 |
0,77837 |
0,0001 |
1 |
Y |
0 |
Signifikan |
|
f2 |
0,47697 |
0,0179 |
2 |
Y |
0 |
Signifikan |
|
w1 |
2,44988E-6 |
<,0001 |
0 |
X1t |
0 |
Signifikan |
|
w2 |
1,54260 |
0,0058 |
0 |
X21,t |
1 |
Signifikan |
|
w3 |
2,98848 |
<,0001 |
0 |
X22,t |
1 |
Signifikan |
|
w4 |
1,80873 |
0,0026 |
0 |
X23,t |
0 |
Signifikan |
|
w5 |
-1,53507 |
0,0097 |
1 |
X23,t |
0 |
Signifikan |
|
w6 |
2,07939 |
0,0002 |
0 |
X25,t |
0 |
Signifikan |
|
w7 |
6,50381 |
<,0001 |
0 |
X26,t |
0 |
Signifikan |
|
w8 |
1,11309 |
0,0618 |
0 |
X27,t |
1 |
Signifikan |
|
w9 |
-1,02743 |
0,0835 |
1 |
X27,t |
1 |
Signifikan |
|
w10 |
1,47657 |
0,0082 |
0 |
X35,t |
0 |
Signifikan |
|
w11 |
1,38938 |
0,0127 |
0 |
X41,t |
1 |
Signifikan |
|
w12 |
1,78885 |
0,0016 |
0 |
X28,t |
1 |
Signifikan |
Tabel 20. Hasil Uji White Noise Residual Model ARI-MAX Dengan Input Gabungan Data Metrik dan Non Metrik
|
Lag |
Chi-Square |
DF |
p-value |
Keputusan |
|
6 |
1,93 |
4 |
0,7488 |
White Noise |
|
12 |
10,03 |
10 |
0,4381 |
White Noise |
|
18 |
17,67 |
16 |
0,3435 |
White Noise |
|
24 |
22,05 |
22 |
0,4568 |
White Noise |
|
30 |
28,77 |
28 |
0,4243 |
White Noise |
|
Tabel 21. Hasil Uji Normalitas Residual Model ARI- | |
|
MAX Dengan Input Gabungan Data Metrik | |
|
dan Non Metrik | |
|
Test D_hitung p-value |
Keputusan |
|
Kolmogorov- Smirnov 0,05205 0,1500 |
Berdistribusi Normal |
dapat disimpulkan bahwa residual telah memenuhi asumsi berdistribusi normal.
-
b. Pembentukan model ARIMAX dengan input gabungan data metrik dan non metrik berdasarkan model Intervensi.
Hasil Estimasi dan Uji Signifikansi Parameter Model ARIMAX dengan input gabungan data metrik dan non metrik berdasarkan model intervensi terlihat pada Tabel 4.23. Dengan menggunakan taraf signifikansi 10 % semua parameter signifikan dimana nilai p-value di bawah 0,01.
Tabel 20 menunjukkan hasil uji white noise residual model ARIMAX dengan input gabungan data metrik dan non metrik. Dengan taraf signifikansi 5 % semua
lag telah memenuhi asumsi white noise, dimana memiliki nilai p-value lebih besar dari 0,05.
Yt = 0,00000024X 1t -1,54260X21tt-1 - 2,98848X22,t-1
-
- 1,80873X23tt +1,53507X23,t - 2,07939X25,t
-
- 6,50381X26,t -1,11309X27,t +1,02743X27,t-1
-
- 1,47657X351 -1,38938X41. , -1,78885X2
51 1 tl-1 8 ,t-1
at
+
(1 - 0,77837B - 0,47697B2)
………………..(26)
Pengujian asumsi kenormalan d engan uji Kolmogorov-Smirnov dengan taraf signifikansi 5 % memiliki nilai p-value lebih besar dari 0,05. Sehingga dapat disimpulkan bahwa residual telah memenuhi asumsi berdistribusi normal.
Identifikasi Heteroskedastisitas pada Varians Residual Model ARIMAX
Keempat model tersebut telah memenuhi asumsi signifikansi parameter, white noise dan berdistribusi normal. Langkah selanjutnya adalah pendeteksian terhadap adanya heteroskedastisitas pada keempat model tersebut. Hasil deteksi heteroskedastisitas dengan uji Lagrange Multiplier diperoleh bahwa keempat model tidak ditemukan adanya unsur heteroskedastisitas, dimana nilai p-value lebih besar dari alpha (0,05).
Tabel 22. Hasil Uji Heteroskedastisitas Dengan Uji LM Pada Model Intervensi
Tabel 23. Hasil Uji Heteroskedastisitas Dengan Uji LM Pada Model Fungsi Transfer
|
Q and LM Tests for ARCH Disturbances | ||||
|
Order Q |
Pr > Q |
LM |
Pr > LM | |
|
1 |
0.3198 |
0.5717 |
0.2854 |
0.5932 |
|
2 |
0.3350 |
0.8458 |
0.2946 |
0.8630 |
|
3 |
0.6426 |
0.8866 |
0.6652 |
0.8813 |
|
4 |
0.7867 |
0.9402 |
0.7358 |
0.9468 |
|
5 |
1.4578 |
0.9179 |
1.3849 |
0.9260 |
|
6 |
1.5805 |
0.9540 |
1.5419 |
0.9567 |
|
7 |
1.8957 |
0.9654 |
1.8807 |
0.9661 |
|
8 |
1.9383 |
0.9828 |
2.0267 |
0.9802 |
|
9 |
3.0646 |
0.9617 |
2.8846 |
0.9687 |
|
10 |
3.1461 |
0.9778 |
2.9202 |
0.9832 |
|
Q and LM Tests for ARCH Disturbances | ||||
|
Order Q |
Pr > Q |
LM |
Pr > LM | |
|
1 |
0.0472 |
0.8280 |
0.0632 |
0.8015 |
|
2 |
0.0652 |
0.9679 |
0.0838 |
0.9590 |
|
3 |
0.1719 |
0.9820 |
0.1759 |
0.9814 |
|
4 |
0.1721 |
0.9965 |
0.1765 |
0.9963 |
|
5 |
0.4533 |
0.9937 |
0.4825 |
0.9928 |
|
6 |
0.5075 |
0.9977 |
0.5610 |
0.9970 |
|
7 |
1.0445 |
0.9941 |
1.0316 |
0.9943 |
|
8 |
1.1892 |
0.9967 |
1.1782 |
0.9969 |
|
9 |
1.2877 |
0.9984 |
1.2883 |
0.9984 |
|
10 |
2.8102 |
0.9855 |
2.7816 |
0.9861 |
Tabel 24. Hasil Uji Heteroskedastisitas Dengan Uji LM Pada Model Gabungan Berdasarkan Model Fungsi Transfer
Tabel 25. Hasil Uji Heteroskedastisitas Dengan Uji LM Pada Model Gabungan Berdasarkan Model Intervensi
|
Q and LM Tests for ARCH Disturbances | ||||
|
Order Q |
Pr > Q |
LM |
Pr > LM | |
|
1 |
0.4474 |
0.5036 |
0.4890 |
0.4844 |
|
2 |
1.2118 |
0.5456 |
1.2409 |
0.5377 |
|
3 |
1.3771 |
0.7109 |
1.3584 |
0.7153 |
|
4 |
1.4326 |
0.8385 |
1.4687 |
0.8322 |
|
5 |
1.5960 |
0.9017 |
1.9649 |
0.8540 |
|
6 |
1.6023 |
0.9524 |
2.0586 |
0.9142 |
|
7 |
2.4301 |
0.9323 |
3.2170 |
0.8642 |
|
8 |
7.7410 |
0.4592 |
7.7675 |
0.4565 |
|
9 |
7.8717 |
0.5471 |
8.3281 |
0.5015 |
|
10 |
11.2992 |
0.3347 |
10.1671 |
0.4260 |
|
11 |
11.4078 |
0.4098 |
11.1353 |
0.4320 |
|
12 |
14.5980 |
0.2642 |
13.2203 |
0.3532 |
|
Q and LM Tests for ARCH Disturbances | ||||
|
Order Q |
Pr > Q |
LM |
Pr > LM | |
|
1 |
0.4058 |
0.5241 |
0.4382 |
0.5080 |
|
2 |
0.4227 |
0.8095 |
0.4513 |
0.7980 |
|
3 |
0.4293 |
0.9341 |
0.4792 |
0.9234 |
|
4 |
0.9340 |
0.9196 |
0.9170 |
0.9221 |
|
5 |
2.1895 |
0.8224 |
1.9256 |
0.8593 |
|
6 |
2.3812 |
0.8815 |
1.9992 |
0.9198 |
|
7 |
2.5989 |
0.9195 |
2.3037 |
0.9411 |
|
8 |
2.6653 |
0.9536 |
2.3554 |
0.9681 |
|
9 |
3.9113 |
0.9172 |
3.4643 |
0.9430 |
|
10 |
3.9142 |
0.9511 |
3.4904 |
0.9674 |
|
11 |
3.9742 |
0.9707 |
3.6707 |
0.9786 |
|
12 |
8.8426 |
0.7163 |
8.7456 |
0.7245 |
Tabel 26. Kriteria Pemilihan Model ARIMAX Berdasarkan Data In-Sample
Tabel 27. Kriteria Pemilihan Model ARIMAX Berdasarkan Data Out-Sample
|
Model |
AIC |
SBC |
|
Fungsi Transfer |
427.7595 |
442.9443 |
|
Intervensi |
292.8454 |
336.4132 |
|
Gab_berdasarkan model FT |
311.3344 |
353.7605 |
|
Gabberdasarkan model Intervensi |
308.0798 |
351.6476 |
|
Model |
RMSE |
|
Fungsi Transfer |
0,0981 |
|
Intervensi |
0,2301 |
|
Gab_berdasarkan model FT |
0,5049 |
|
Gabberdasarkan model Intervensi |
0,3997 |
Tabel 28. Hasil Ramalan Tingkat Inflasi Kota Denpasar Tahun 2014 Berdasarkan Model Fungsi Transfer
|
Bulan |
Ramalan Aktual Bulan Ramalan Aktual |
|
Januari Februari Maret April Mei Juni |
1,25 1,26 Juli 1,52 - 0,61 0,37 Agustus 0,29 - 0,56 0,32 September 0,15 - 0,26 0,13 Oktober 0,78 - -0,03 - Nopember -0,21 - 0,52 - Desember 0,99 - |
Pemilihan Model Terbaik
Hasil analisis dari ketiga model ARIMAX, model intervensi merupakan model ARIMAX terbaik berdasarkan data in-sample dengan melihat kriteria AIC, SBC memiliki nilai terkecil seperti terlihat pada
Tabel 26.
Sedangkan untuk data out-sample, model terbaik didasarkan pada nilai RMSE terkecil. Berdasarkan Tabel 27 model terbaik untuk data out-sample adalah model fungsi transfer.
SIMPULAN
Berdasarkan rumusan masalah dan pembahasan analisis yang telah dilakukan, maka kesimpulan yang dapat diperoleh adalah sebagai berikut, berdasarkan model ARIMAX yang telah diperoleh, Model ARIMAX terbaik berdasarkan data in-sample adalah model intervensi dengan nilai AIC dan SBC terkecil. Sedangkan berdasarkan data out-sample, model terbaiknya adalah model fungsi transfer dengan nilai RMSE terkecil. Berdasarkan model fungsi transfer yang diperoleh, menunjukkan bahwa ada keterkaitan atau pengaruh secara signifikan antara jumlah wisatawan mancanegara yang datang ke Bali dengan tingkat inflasi Kota Denpasar. Inflasi Kota Denpasar pada bulan ke-t dipengaruhi oleh jumlah wisatawan mancanegara pada bulan ke-t sebesar -0,0000162 dan inflasi Kota Denpasar pada bulan ke-(t-1) dipengaruhi oleh jumlah wisatawan mancanegara pada bulan ke-(t-1) sebesar -0,0000198. Berdasarkan model intervensi yang diperoleh, pengaruh terbesar yang mempengaruhi tingkat inflasi Kota Denpasar berdasarkan waktu kenaikan BBM terjadi pada bulan Oktober 2005 yaitu sebesar 6,23734. Hal ini karena besarnya presentase kenaikan BBM pada bulan tersebut sebesar 126%. Pengaruh terbesar kedua yang mempengaruhi tingkat inflasi Kota Denpasar adalah pada bulan Juni 2001 yaitu sebesar 2,79271, dimana kenaikan BBM pada bulan tersebut sebesar 30%. Sedangkan tingkat inflasi Kota Denpasar yang dipengaruhi oleh kenaikan TDL hanya terjadi pada kenaikan TDL pada bulan Juli 2010 saja. Hasil identifikasi homoskedastisitas varians menunjukkan bahwa semua model tidak mengandung unsur heteroskedastisitas.
SARAN
Saran yang dapat diberikan berdasarkan hasil penelitian adalah, perlu memasukkan faktor-faktor selain jumlah wisatawan mancanegara dalam analisis yang diduga mempengaruhi tingkat inflasi Kota Denpasar. Faktor-faktor tersebut seperti jumlah wisatawan domestik, jumlah uang yang beredar, tingkat suku bunga, kurs dolar AS dan lain sebagainya, agar hasil dari model yang diperoleh untuk peramalan tingkat inflasi lebih akurat.
REFERENSI
Box, G.E., Jenkins, G., & Reinsel, G.C. (1994), Time Series Analysis:Forecasting and Control (3rd ed. ). New Jersey
Bollerslev, T. (1986), A Generalized Autoregressive Conditional Heteroscedasti-city. Journal of Econometrics, vol.31:307-327
BPS Provinsi Bali, 2000-2013, Bali Dalam Angka
Engle, R.F. (1982), Autoregressive Conditional Heterosce-dasticity with Estimats of Variance of U.K.Inflation. Econometrics, vol. 50:987-1008
Hasbullah, J. (2012), Tangguh dengan Statistik akurat dalam membaca Realita Dunia, penerbit Nuansa Cendikia.
Kismiantini & Dhoriva(2010), Dampak penurunan harga BBM jenis Premium terhadap angka Inflasi kota Yogyakarta menggunakan model Intervensi dengan Step Fungsi Edisi Khusus Seminar Nasional Matematika, UNY, Yogyakarta, 5 Desember 2009.
Makridakis, S., Weelwright, S.C., & McGee.,V.E(1999), Metode dan Aplikasi Peramalan. Edisi kedua jilid I penerbit Erlangga
Rokimah, N. J. (2012), Pendekatan Fungsi Transfer dan Artificial Neural Network untuk Meramalkan Inflasi Jawa Timur. Tesis S2, Institut Teknologi Sepuluh Nopember Surabaya
Wei, W.W.S. (2006), Time Series Analysis Univariate and Multivariate Method, Second Edition. Pearson Addison Wesley, USA
Nuvitasari, E. (2009), Analisis Intervensi Multi Input Fungsi Step dan Pulse untuk Peramalan kunjungan Wisatawan ke Indonesia, Tesis S2 Statistika, ITS, Surabaya.
Santoso, Teguh (2011), Aplikasi Model GARCH pada Data Inflasi Bahan Makanan Indonesi peroode 2005.1-2010.6. Jurnal Organisasi dan Management, volume 7, nomor 1, Maret 2011, 38-52. Diakses dari http://www.lppm.ut.ac. id , 19 Mei 2013
Suhartono (2007), Teori dan Aplikasi Model Intervensi Fungsi Pulse, Jurnal Ilmiah MatStat, Vol. 7, No. 2, hal. 191-214.
Sumaryanto (2009), Volatilitas Harga Eceran Beberapa Komoditas Pangan Utama dengan Menggunakan Model ARCH dan GARCH. Jurnal Agro Ekonomi, Volume 27 No.2, Oktober 2009:135-163. Diakses dari http://www. pse.litbang.deptan.go.id pada 21 Agustus 2013
Widarjono, A. (2002), Aplikasi Model ARCH Kasus Tingkat Inflasi di Indonesia. Jurnal Ekonomi Pembangunan, Kajian Ekonomi Negara Berkembang Hal. 71-82.
182
Discussion and feedback