Optimization of Placement and Size of Distribution Generators Using Quantum Genetic Algorithms to Improve Power Quality in Bali Distribution Networks

Journal of Electrical, Electronics and Informatics, Vol. 3 No. 1, February 2019

1

Optimization of Placement and Size of Distribution Generators Using Quantum Genetic Algorithms to Improve Power Quality in Bali Distribution Networks

Yanu Prapto Sudarmojo ^1*, Antonius Ibi Weking²

• ^1,2 Departement of Electrical Engeneering

Faculty of Engeneering

Udayana University

Bali- Indonesia 80361

*[email protected]

Abstract-Bali is a tourist area with resources originating from Java and several large-scale factories that use oil and gas, which until now still need more electricity. The addition of small-scale generators in Bali is very helpful where economic benefits are distribution costs and reduction in transmission costs, electricity costs and fuel savings. Technically, DG distributors must be done correctly and optimally from size or location so as to provide maximum results from an economic perspective, minimizing electricity losses and increasing the voltage profile which results in an increase in electricity quality. For this reason, this study will use heuristic optimization using the Quantum Genetic Alghorithm method to place generators distributed to the Bali Electricity Network. To calculate electricity losses and voltage profiles, the method used to solve them is the Newton Raphson method.

A result of this study, DG was installed in a feeder located in Abang District, Karangasem Regency where Abang Feeder had a total of 431 buses that were part of the Bali Distribution System. By using QGA, DG is installed on buses 1, 5, 7, and 302 with capacities of each DG is 0.374 MW, 1.894 MW, 1.988 MW and 0.500 MW, after installation of DG, the voltage profile can be repaired. The voltage profile for several buses to Abang Feeder can be fixed from 0.83 pu to 0.98 pu. Electricity losses from 1.105 MW to 0.234 MW

Index Term : Optimation, Distributed Generator (DG), Quantum Genetic Alghorithm, Voltage Profile, Electricity Loss.

• I.    introduction

Electricity requirements in Bali that are increasing every year must be balanced with an increase of electricity supply. Concerns about economic problems and environmental pollution encourage to increasing in development that supports small-scale generators to be connected close to distribution networks or near load centers. [1][2] To meet this urgent requirements, the distribution of small-scale generators from renewable energy such as Micro Hydro Power Plants, etc. which are connected to the PLN electricity network is due to the decreasing voltage in several loads which increases power losses. PLN standardizes the normal voltage from 0.9 pu to 1.05 pu. where in some of the load stress is brought in 0.9 pu and this matter needs to be stabilized. [3]

Installation of Distribution Generator (DG) has several advantages in economic, environmental and technical terms. Benefits from economic is reduce transmission distribution and costs, electricity prices and fuel economy. [4][5][6] Planning an electrical system with distribution generator depend of several factors, such as: the number and capacity of the unit, the best location, the best technology to be used, the network connection method. For large networks, software is needed to calculate it.

This research to use Quantum Genetic Algorithm (QGA) combined with Newton Raphson power flow to optimize the placement and size of Distribution Generators (DG) in the Bali distribution system to improve the quality of electric power.

• II.    METHOD

• A.    Power System Distribution Network.

Electric power centers are generally located far from the center of the load. Electrical energy produced by the generation center is channeled through the transmission network. Generator of generator voltage is relatively low (6 kV - 24 kV) where this voltage is raised with a power transformator to a higher voltage of 150 kV - 500 kV. The purpose of increasing this voltage, in addition to enlarging the conductivity of the channel (directly proportional to the square of the voltage), is also to minimize power losses and voltage losses in the transmission line. The reduction in voltage from high extra high voltage networks before to consumers is done twice. The first is done at the substation (GI), reducing the voltage from 500 kV to 150 kV or from 150 kV to 70 kV. The second is done at a distribution substation from 150 kV to 20 kV or from 70 kV to 20 kV. The power line from the source of the power plant to the last transformator, often referred to as the transmission line, while from the last transformator, until the last consumer is called the distribution channel or primary channel. The distribution system voltage can be grouped into 2 major parts, namely:[7]

• 1.    Primary Distribution (20kV)

The 20kV distribution network is often called the Medium Voltage Distribution System. Networks In the medium voltage distribution system (Primary 20kV) can be grouped into five models, namely the Radial Network, The Connecting Network (Tie Line), Circle Network (Loop), Spindle Network and Cluster Systems.

• 2.    Secondary Distribution (380/220V).

The 380 / 220V distribution network is often called a secondary distribution network or called the 380 / 220V Low Voltage Network.

• B.    Newton Raphson Method

Newton Raphson (N_R) is a method that is often used in power flow analysis to calculate system losses and stresses on each system bus. In the use of several things known as: [8]

Power Injection

Power on Bus i :

s*t=v_l-∑‰ιY_ikv_k (i)

Updated variables after k iterations :

∆5(^k+1) = ∆δ"( + ∆δ_i(2)

l½l(^k+1) = ∣VJ∞ = ∆∣V∣(3)

Channel power flow :

Power flow from bus i ke bus j :

S_ij=V_iIl_j=V_i^‰V_iY_ij0< ...(4)

Power flow from bus j ke bus i :

'.. vij v i' ' ■ v_ij,..; ...(5)

Channel losses :

∑bus no ^—^bus no

„1 >j.i ^⁺

= ∑b,^u1 ^no∑b*Γ^o{Cp,j + <⅛) + ⅛ +

O          (6)

• C.    Quantum Genetic Algorithm (QGA)

Quantum Genetic Method Algorithm is based on the concepts of quantum bits (cubite) and superpositions of quantum mechanical forms. The smallest information is stored in two forms of quantum numbers called quantum bits or cubits. Kubit may be in the '1' or '0' state / status, or the superposition of both. The status of the cubite can be shown as the following equation: [9][10]

l^) = H² + l∕Ψ(7)

Where α and β is a complex number that corresponds to the probability of the amplitude of the state. Normalization from the states is:

H² + l∕Ψ = ι(8)

QGA is based on the concept of cubite. One cubit is defined to consist of a number pair (α,β) as follows :

H(9)

Which is the equation of the equation (8) dan (9). For m cubits represented as the following matrix below :

KIMI(10)

Where,

^l^^lL + ^lβi∖² = 1, i = 1,2,3...m

This representation has the advantage of being able to represent several superpositions of circumstances. For an easier understanding, here

the following example: three cubits with three pairs of numbers as follows:

Iffl.........................^ιι1^ι

The three pairs of numbers above can be represented as follows:

000 +0001 +     010 +0001 +

2222

100 +0101 +     110 +0111

2222

This result shows that the probability of state ∣000),∣010),∣100) and ∣110) is - , ¹ , - dan ¹.

∆θ_i = ∆f_i × sign(a_b — aj) × sign[βj × si∏ ∆f_i — a_j × (1 — cos∆f_i) ](14)

where :

^ⁱ=M¹-Tsfflⁱ = ¹-².....n) (15)

sign(a_b — a_j) =

(+1 ifa_b ≥ aj (—1 ifa_b < aj

(16)

sign[βj × si∏∆f_i — a_j∙ × (1 — cos∆f_i)]

(+1 ifβ_j∙ × si∏∆f_i ≥ a_j∙ × (1 — cos∆f_i) [—1 ifβ_j∙ × si∏∆f_i < a_j∙ × (1 — cos∆f_i)

Three cubite systems from equation (11) have four types of information at the same time. Evolutionary calculations by representing cubits that have diverse characteristics, are better than the classical approach because they can represent every situation. One cubit string like equation (11) can represent four states (status). Convergence can also be obtained by qubit representation. As ∣a∣²or ∣β∣² the approach to 1 or 0, converges the qubit string to a single state and the property of diversity disappears gradually. That means, qubit representations can have two characteristics of exploration and exploitation simultaneously.

(17)

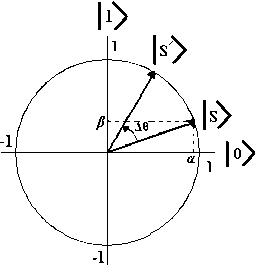
Fig. 1. Basic of Quantum bits (cubite)

D. Problems in formulation :

Rotation Gate /Q-gate

Gate Rotation (Quantum-gate) is defined as the operator of the QGA variation, where the updated qubit operation must meet the normalization conditions, ∣a'∣² + ∣β^,∣² = 1 , where a' and β' are updated qubit values.

Rotation Gate Equation as follows:

Ifflffl-Iffl=--) ……..(12)

Γcos∆θ_i — si∏∆0;],. _a . Λ_i(t}=   .                    (i = 1,2,, n)

• ¹       [si∏∆θ_i    cos∆θ_i

……..(13)

∆θ_i is the angle of rotation (figure 1) of each member of the population. Rotation angle ∆θ_i is related to differences in normalization ∆f_i between the achievements of each member of the population and the best optimal global.

Equation for ∆θ_i:

Objective Function

(n —V AusnovbBsnofc

^min     = ∑_i*₁  ∑j*₁ (O"j ⁺

⅝)}(18)

Voltage Limitation

∣½ _mJ ≤ ∣½∣ ≤ ∣K _maχ∣ (19)

DG Capacity Limitation

PDG min ≤ PDG ≤ PDG max ∙ ∙ ∙ ∙ ……….. (20)

• E. QGA implementation for optimization of location and size of DG.

• 1.    t = 0

• 2.    Initialize a population from n population (qubit string)

Q(0) = {qι(0),q2(0),∙∙∙,q_n(0)}

Every qubit string representating : α+(0) α2(0)     αm(0)

q¹⁽⁰⁾ = llβι(0)l Iβ2(0)l “ lβm(0)U

• 3.    For all qubit strings initialize amplitude amplification at:

qι(θ) =

4.

Create randomly binary solutions with observing state Q(0) :

P(O) = {p1(O),P2(O),-,p_n(O)}

In this study, each DG is representative of an 8-bit binary number. MSB signifies where the DG is located. If the bit is 1, DG will appear on the bus and DG output will be determined from the remaining 7 bits and also based on Pmin and Pmax from the input parameter matrix. If MSB = 0, the DG will not appear on the bus but as a load bus. Assess each p₁(0) (i = 1,2, —,n) and prepare the data bus matrix.

• 5.    Using the data bus, run the load flow and get the loss.Hitung fungsi objektif dan menyimpan nilai fitnessnya.

• 6.    Perform steps 5-7 for each member of the population.

• 7.    Find members of the population that have the highest objective function and are stored in the winner's place (iteration).

• 8.    Next Iteration (t=t+1)

• 9.    Generate the next population from the existing population with the rotation of each existing member so that the new generation gets closer to the winner, see figure 1. Rotation is solved by the rotation of the matrix which has been calculated through equations (12) –(17)

• 10.    Preform steps 4, 5, dan 6 as much as needed.

• 11.    The most optimum solution is the last iteration.

• III.    RESULT AND DISCUSION

• A.    Measurement and Location Data

This study uses measurement data and secondary data on feeder Abang located in the eastern part of Bali province precisely in Karangasem Regency. Feeders who are in the area of PT. PLN (Persero) This East Bali Area has a total channel length of 207.946 Km. The total number of buses found in Penyulang Abang is 431 with the system working on a 20 kV system with an electrical power supply from the GI Amlapura of 150 kV then connected to the GI transformer to be reduced to 20 kV. [11]

Abang feeder is a feeder that uses a radial configuration type where between the point of the power source and the load point is in a straight

line. The point of the electricity source and the end point in the feeder has a distance of 207.946 Km, because the distance decreases the voltage profile.

TABLE 1

LOAD DATA VOLTAGE BELOW 0.9 PU

BUS	BUS INPUT	MAG	ANG	LOAD		GENERATOR
				MW	Mvar	MW	Mvar
319	401	0.83	-5.9	0.024	0.015	0	0
249	402	0.86	-4.9	0	0	0	0
250	403	0.83	-6.1	0.026	0.016	0	0
251	404	0.86	-4.9	0	0	0	0
252	405	0.85	-5.4	0.011	0.007	0	0
256	406	0.86	-4.9	0	0	0	0
255	407	0.84	-5.9	0.02	0.013	0	0
259	408	0.86	-4.9	0	0	0	0
257	409	0.86	-4.9	0	0	0	0
258	410	0.85	-5.4	0.01	0.006	0	0
323	411	0.86	-4.9	0	0	0	0
324	412	0.85	-5.3	0.009	0.006	0	0
260	413	0.86	-4.9	0	0	0	0
262	414	0.85	-4.9	0	0	0	0
336	415	0.85	-5	0.003	0.002	0	0
326	416	0.86	-4.9	0	0	0	0
261	417	0.85	-5.1	0.004	0.003	0	0
330	418	0.86	-4.9	0	0	0	0
328	419	0.85	-5.2	0.007	0.004	0	0
333	420	0.86	-4.9	0	0	0	0
334	421	0.83	-6	0.024	0.15	0	0
343	422	0.86	-4.9	0	0	0	0
341	423	0.86	-4.9	0	0	0	0
340	424	0.85	-5.1	0.004	0.003	0	0
347	425	0.85	-4.9	0	0	0	0
346	426	0.83	-6	0.024	0.015	0	0
350	427	0.86	-4.9	0	0	0	0
348	428	0.86	-4.9	0	0	0	0
263	429	0.85	-5.1	0.004	0.003	0	0
253	430	0.86	-4.9	0	0	0	0
252	431	0.83	-6	0.024	0.015	0	0

Based on the simulation using the lowest voltage ETAP profile on feeder brother is equal to 0.83 p.u or 16.6 kV found on buses 401, 403, 421, 426 and 431 with a total power loss of 1.105 MW. The allowable stress profile is between 0.9 - 1.05 or 18 kV - 21 Kv. Because of these problems, the stress profile must be improved by installing several DGs on several buses with certain capacities so that a bad voltage profile can achieve the allowable voltage profile value.

• B.    Field data testing

Measurement data and secondary data on Abang feeder located in the eastern part of Bali province precisely in Karangasem Regency. Feeders who are in the area of PT. PLN (Persero) East Bali Area has a total channel length of 207.946 Km.[11] The total number of buses found in Abang feeder is 431. Abang feeder are feeders who use radial configuration types where between the point of the power source and the load point are in a straight line. Based on the simulation using the lowest voltage ETAP profile on feeder brother is 0.83 p.u or 16.6 kV found on

buses 401, 403, 421, 426 and 431. By using the QGA program the results obtained are as follows:

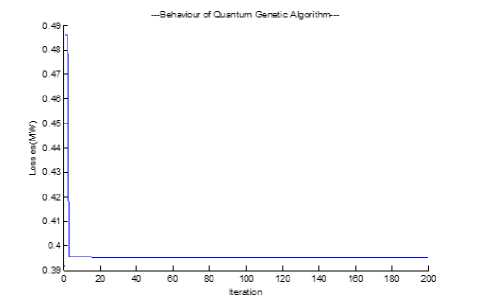
Fig. 2. Graphics of Abang Feeder Simulation Results With QGA

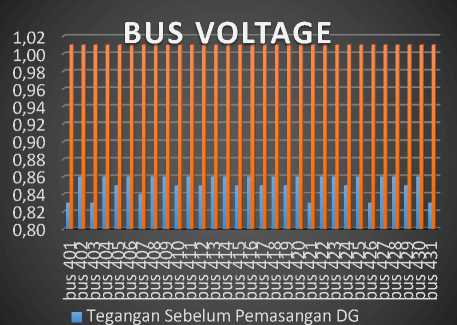
Fig. 3. Voltage Repair with QGA

From the results of running the program of Distribution Generator (DG) is installed on buses 1,5,7 and 302 with a sequence of capacities of 0.374 MW, 1.894 MW, 1.988 MW and 0.500 MW where the total installation is 4.756 MW. Voltage profiles can also be improved as shown in Fig. 3. Likewise, the channel power loss from the previous power loss is 1.105 MW reduced to 0.234 MW.

• IV.    CONCLUSION

Of the total number of buses in Penyulang Abang there are 431 Distribution Generators (DG) placed on several buses to improve the overall voltage profile. From the results of running the program (Running) on Abang feeder, the Distribution Generator (DG) is installed on buses 1,5,7 and 302 with a sequence of capacities of 0.374 MW, 1.894 MW, 1.988 MW and 0.500 MW where the total installation is 4.756 MW.

The previous power loss was 1.105 MW, reduced to 0.234 MW.

ACKNOWLEDGMENT

The researcher are very greatful to research and community service of udayana university and ministry of research, technology and higher education with contribution conducting research compotitive grant scheme, so that the research could be conducted.

REFERENCES

• [1]    Budiman. A, Breeder, 2010, Genetic Algorithm Multiobjective for Sizing and Placement of Distributed Generator.

• [2]    Carmen L.T.Borges, Djalma M.Falcao, 2006, Optimal distributed generation for reliability, losses and voltage improvement. ELSEVIER Electrical Power and Energy System28(1006) 4130-420.

• [3]    SPLN 72. 1987. Spesifikasi Desain untuk Jaringan Tegangan Menengah (JTM) dan Jaringan Tegangan Rendah (JTR). Keputusan Direksi PLN No. 060/DIR/87

• [4]    Celli G, Ghiani E, Mocci S, Pilo F. A multiobjective evolutionary algorithm for the sizing and siting of distributed generation. IEEE Trans Power Syst 2005;20(2):750–7.

• [5]    G.N.Koutroiumpezis, A.S.Safigianni, 2010, Optimimum allocation of the maximum possible distributed generation penetration in a distribution network. ELSEVIER Electric Power System Research 80, 1421-1427, June 2010

• [6]    Sudipta Ghosh, S.P. Ghoshal, Saradindu Ghosh, 2010, Optimal sizing and placement of distributed generation in a network system, ELSEVIER, Electrical Power and Energy Systems 32, 849–85

• [7]    PT. PLN (persero). 2010. Kriteria Desain Enjiniring Konstruksi Jaringan Distribusi Tenaga Listrik. Buku 1.

• [8]    Saadat Hadi, Power System Analysis, McGrawHill, International Editions 1999

• [9]    Aryani Ni ketut, Abdillah M, Negara Y M, and Soeprijanto A, (2011), “ Distributed Generator Using Quantum Genetic Algortihm for Reducing Losses and Improving Voltage Profile”, IEEE Conference Publication, pp.108-112

• [10]    John G. Vlachogiannis a,*, Jacob Østergaard, 2009, Reactive power and voltage control based on general quantum genetic algorithms ELSEVIER , Expert Systems with Applications 36 6118–6126

• [11]    PT PLN (persero) Distribusi-Bali