Application Design of Newton-Rapshon method in Proving Maximum Wavelength on Wien’s Displacement Law
on
Application Design of Newton-Rapshon method in Proving Maximum Wavelength …………
(I Gusti Agung Widagda, dkk)
Perancangan Aplikasi Metode Newton-Rapshon
Termodifikasi dalam Pembuktikan Panjang Gelombang Maksimum pada Hukum Pergeseran Wien
Application Design of Newton-Rapshon method in Proving Maximum Wavelength on Wien’s Displacement Law
I Gusti Agung Widagda1*, Ni Luh Putu Trisnawati1, I Wayan Gede Suharta1
1Program studi Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana, Kampus Bukit Jimbaran, Badung, Bali, Indonesia 80361
Email: *igawidagda@unud.ac.id; trisnawati@unud.ac.id; suharta@unud.ac. id
Abstrak – Perhitungan panjang gelombang maksimum (λm) dari radiasi yang dipancarkan benda hitam dapat ditentukan dari Hukum pergeseran Wien, yang menyatakan perbandingan antara konstanta Wien dengan suhu mutlak (T). Hukum pergeseran Wien bisa diturunkan secara analitik dari persamaan Kerapatan Energi (Uλ) pada hukum Plank. Penyelesaian Uλ diperoleh dengan menghitung turunan pertama dari fungsi tersebut terhadap λ atau dUλ/dλ, dan dilanjutkan dengan mencari solusi dari persamaan turunan tersebut. Solusi dari dUλ/dλ adalah nilai λ yang membuat dUλ/dλ sama dengan nol. Panjang gelombang yang dihasilkan adalah merupakan panjang gelombang maksimum λm, yaitu nilai panjang gelombang yang membuat nilai pada persamaan Uλ bernilai maksimum. Hasil akhir dari perhitungan ini adalah hukum pergeseran Wien yaitu perkalian λm dengan T sama dengan konstanta Wien. Jadi pada dasarnya penurunan hukum pergeseran Wien adalah mencari nilai maksimum dari fungsi f(x). Nilai maksimum dari fungsi f(x) bisa dilakukan secara numerik. Penyelesaian secara numerik bisa dilakukan dengan metode Newton-Rapshon Termodifikasi. Metode Newton-Rapshon termodifikasi biasanya diimplementasikan dalam bentuk kode program komputer. Pada penelitian ini diperoleh hasil perhitungan panjang gelombang maksimum λm secara analitik sangat mendekati hasil perhitungan numerik (NR termodifikasi). Hal ini bisa dilihat dari hasil regresi linear dengan nilai gradien (m), konstanta regresi (c )dan koefiesien determinasi (R2) mendekati nilai ideal yaitu 1, 0 dan 1, secara berurutan.
Kata kunci: Hukum pergeseran Wien; metode Newton-Rapshon; hukum Planck; radiasi benda hitam.
Abstract – The Calculation of the maximum wavelength (λm) of radiation emitted by a black body can be determined from the Wien displacement law, which states the ratio between the Wien constant and the absolute temperature (T). Wien's displacement law can be derived analytically from the Energy Density equation (Uλ) in Plank's law. The solution for Uλ is obtained by calculating the first derivative of the function with respect to λ or dUλ/dλ, and then proceeding with finding a solution to the equation for the derivative. The solution of dUλ/dλ is the value of λ that makes dUλ/dλ equal to zero. The resulting wavelength is the maximum wavelength λm, which is the wavelength value that makes the value in the equation Uλ the maximum value. The final result of this calculation is the Wien’s displacement law, namely the multiplication of λm with T equals the Wien constant. So basically, the derivation of Wien's displacement law is to find the maximum value of the function f(x). The maximum value of the function f(x) can be done numerically. Solving numerically can be done with the Modified Newton-Rapshon method. The modified Newton-Rapshon method is usually implemented in the form of computer program code. In this research, the results of the calculation of the maximum wavelength λm analytically are very close to the results of numerical calculations (modified NR). This can be seen from the results of linear regression with gradient values (m), regression constants (c) and coefficient of determination (R2) close to the ideal values of 1, 0 and 1, respectively.
Keywords: Wien’s displacement law; Newton-Rapshon method; Planck’s law; black body radiation.
Benda yang menyerap semua radiasi cahaya yang mengenainya disebut dengan benda hitam (blackbody)
[1, 2]. Benda hitam memiliki nilai koefisien absorbsi (a), refleksi (r) dan transmisi (t), masing-masing 1, 0 dan 0, secara berurutan. Benda akan mengalami perubahan warna jika benda tersebut dipanaskan. Pertama warna benda berubah jadi merah, kemudian kuning, dan akhirnya pada suhu tertentu warnanya menjadi putih. Benda yang mengalami pemanasan akan memancarkan radiasi. Radiasi yang dipancarkan benda hitam memiliki panjang gelombang maksimum λm berbeda-beda tergantung pada temperatur dari benda tersebut.
Relasi antara nilai temperatur T dan panjang gelombang maksimum λm radiasi dari benda hitam sesuai dengan hukum pergeseran Wien. Jika benda hitam temperaturnya ditingkatkan maka akan dipancarkan radiasi gelombang elektromagnetik (EM) dengan λm yang semakin pendek. Namun sebaliknya, jika suhu benda tersebut diturunkan maka akan memancarkan radiasi gelombang EM dengan λm semakin panjang. Jadi relasi antara λm dengan T berbanding terbalik. Secara matematis persamaan hukum pergeseran Wien dapat diturunkan dari persamaan Plank. Persamaan kerapatan energi pada benda hitam,Uλ, pada persamaan Plank bisa dipakai untuk menurunkan hukum pergeseran Wien secara analitik [3]. Besarnya nilai λm pada persamaan Uλ bisa dihitung dari turunan Uλ terhadap λ, yang selanjutnya disamakan dengan nol. Hasil akhir dari solusi secara analitik akan didapatkan hukum pergeseran Wien yaitu: hasil kali λm dengan T sama dengan konstanta yang besarnya 2,898 x10-3.
Solusi dari persamaan f(x) adalah nilai x yang membuat f(x) menjadi 0. Solusi dari f(x) sering disebut akar f(x). Solusi ini bisa dicari baik secara analitik maupun secara numerik. Solusi analitik adalah solusi dengan menggunakan uraian matematika. Sedangkan solusi secara numerik dengan menggunakan algoritma atau metode tertentu yang bisa diimplementasikan ke dalam program komputer. Untuk mendapatkan solusi dari suatu fungsi (x) secara numerik bisa dilakukan dengan beberapa metode seperti: Bisection, Secant, Newton-Rapshon, Brent dan lain-lain [4, 5]. Metode Newton-Rapshon (NR) merupakan metode yang banyak dipakai karena proses iterasinya berlangsung dengan cepat [6]. Metode NR bisa juga dipakai untuk mencari turunan pertama dari fungsi (f’(x)) dengan jalan memodifikasi persamaan NR orisinil menjadi persamaan NR termodifikasi. Metode NR biasanya diimplementasikan ke dalam program komputer sehingga solusi f(x) bisa diperoleh dengan lebih cepat [7].
Berdasarkan uraian diatas maka pada penelitian ini akan dibuat program aplikasi dengan metode NR termodifikasi untuk mencari solusi panjang gelombang maksimum λm pada persamaan kerapatan energi radiasi dari benda hitam Uλ. Akhirnya kita juga bisa menentukan apakah λm yang dihasilkan NR termodifikasi sesuai hasil perhitungan dengan menggunakan hukum pergeseran Wien.
Persamaan kerapatan energi Uλ dalam hukum distribusi Plank sebagaimana Persamaan (1) [7, 8].
U λ
8πhc
λ5 (ehc/λkT - 1)
(1)
dimana, h, c, k, λ dan T, secara berurutan, adalah konstanta Planck, kecepatan cahaya, konstanta Boltzman, panjang gelombang dan suhu dalam satuan Kelvin (K). Nilai-nilai dari parameter h, c dan k masing-masing 6,63 x10-34 Js, 3,0 x108m/s, 1,38 x 10-23 J/K, secara berurutan. Persamaan kerapatan energi pada Persamaan (1) tergantung pada dua buah variabel yaitu: Temperatur mutlak (T) dan panjang gelombang (λ). Satuan dari T adalah K dan λ dalam m. Pada Gambar 1 diperlihatkan kurva Uλ untuk T = 5000 K.
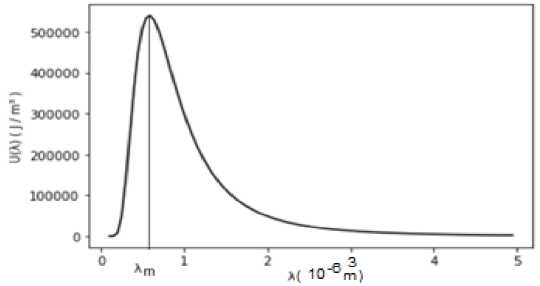
Gambar 1. Kurva kerapatan energi Uλ untuk T = 5000 K.
Nilai maksimum panjang gelombang λm dapat ditentukan dengan menghitung turunan pertama dari Uλ yang sama dengan nol yaitu:
= 0
(2)
j λm
- 5 1 λ2 kT
---:--:—-------τ:—----------—
66 ^hc/λkT i ^5 (-^hc/λkT ∣^2
hc ehh / λkT
= λkT ehh/λkτ -1
hc
Andaikan x =----, Persamaan (4) berubah menjadi:
λkT
ex
5
(5 - x)
x = ln5 — ln(5 — x)
Solusi dari Persamaan (6) adalah:
x = 4,965
sehingga hc
λkT
= 4,965
Persamaan (8) bisa dinyatakan dengan Persamaan (9) yaitu:
λm T = —hh— m k(4,965)
Jika kita menginput nilai h,k dan c ke Persamaan (9) diperoleh:
λm T = 2,898.10-3
Persamaan (10) bisa dinyatakan dengan:
λ =b
λm T = b atau m t
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
b adalah konstanta Wien yang nilainya adalah 2,898 10-3 mK [9]. Persamaan (11) disebut dengan hukum Pergeseran Wien.Persamaan ini dipakai untuk menjelaskan hubungan antara kerapatan energi radiasi (Uλ) dengan panjang gelombang (λ) dan suhu T. Gambar 2 memperlihatkan hubungan antara kedua variabel tersebut.Tampak pada Gambar 2, kurva Uλ pada temperatur: T1, T2, T3 dan T4. Nilai temperatur T1<T2<T3<T4. Semakin tinggi temperatur maka nilai maksimum dari Uλ terjadi pada panjang gelombang λ yang semakin pendek. Nilai panjang gelombang ketika Uλ bernilai maksimum disebut dengan panjang gelombang maksimum (λm).

Gambar 2. Kurva kerapatan energi Uλ untuk beberapa nilai temperatur T.
-
2.2 Metode Newton-Rapshon (NR) termodifikasi
Metode Newton-Rapshon adalah metode untuk menghitung penyelesaian atau akar-akar dari fungsi f(x) secara numerik. Bentuk umum dari metode NR berbentuk persamaan iterasi sehingga metode NR sering
disebut dengan iterasi Newton-Rapshon. Iterasi NR dinyatakan dengan Persamaan (12).
xi+1
= xi
f(x) f '(x)
(12)
dimana i adalah index yang nilainya dari 0,1,2,...n (n adalah jumlah iterasi). f’(x) adalah turunan pertama dari fungsi f(x). Persamaan (12) berupa iterasi yaitu proses berulang dimana nilai x selanjutnya (xi+1) ditentukan oleh nilai x saat ini (xi). Jika selisih dari 2 nilai x yang berurutan sangat kecil atau sama dengan nol maka proses iterasi akan berhenti, seperti dinyatakan pada Persamaan (13) atau (14). Bilangan yang sangat kecil dinyatakan dengan ε.
X1+1 - X1 = 0 (13)
atau
xi+1 - xi ≤ ε
(14)
Iterasi Newton-Rapshon diperluas pemakaiannya yaitu untuk menghitung solusi dari turunan fungsi f(x) atau f’(x). Dalam hal ini adalah mencari nilai x yang membuat nilai f(x) = 0. Solusi dari fungsi f’(x) ini bisa kita diperoleh dengan memodifikasi Persamaan (12) menjadi:
xi+1= Xi - f^- (15) i+1 i f "(x)
f’(x) dan f’’(x), secara berurutan, menyatakan turunan pertama dan turunan kedua dari f(x). Nilai f’(x) dan f”(x) dapat ditentukan secara numerik dengan beberapa metode seperti: beda maju, beda mundur, beda Sentral [10]. Jika kita memakai metode beda sentral makaf(x) danf”(x) dinyatakan dengan Persamaan (16) dan Persamaan (17).
f ’(x) =
f (x + h) - f (x - h) 2h
(16)
f "(x) =
f (x + h) - 2 f (x) + f (x - h ) h2
(17)
Dengan memasukkan Persamaan (16) dan (17) pada Persamaan (15) maka akan diperoleh persamaan yang disebut dengan iterasi Newton-Rapshon termodifikasi yang dinyatakan dengan Persamaan (18).
xi+1 = xI
—
h f (X + h) - f (X - h)
2 f (xl+ h)-2f (Xi) + f (Xi-h)
(18)
variabel h adalah nilai interval yang berupa bilangan yang nilainya kecil. Persamaan iterasi Newton-Raphson termodifikasi ini biasanya diimplementasikan dalam bentuk kode program komputer.
-
2.3 Perhitungan panjang gelombang maksimum λm pada Hukum Pergeseran Wien secara numerik
Penentuan panjang gelombang maksimum λm dalam hukum pergeseran Wein dapat dilakukan secara numerik dengan mencari nilai maksimum dari persamaan kerapatan energi radiasi benda hitam Ui, pada Persamaan (1).
ττ _ 8πhc
-
λ = λ(ehc / λkT -1)
Kita bisa mengkonversi Persamaan (1) menjadi fungsif(x) dengan memisalkan λ = x sehingga menjadi:
f ( x ) =
8πhc
λ(eh/xkT -1)
(19)
Sehingga nilai panjang gelombang maksimum (λm) pada Persamaan (1) bisa dicari dengan menghitung nilai x maksimum (xm) pada Persamaan (19). Nilai x maksimum dari Persamaan (19) bisa diperoleh dengan menghitung penyelesaian dari turunan pertama dari f(x), yang dinyatakan dengan:
.f'(x) = fx) = 0 (20) dx
Untuk menyelesaikan Persamaan (20) ini kita bisa memakai persamaan iterasi NR termodifikasi yang dinyatakan pada Persamaan (18). Proses iterasi pada diawali dengan memberikan nilai x awal (x0). Nilai index iterasi diawali dari i = 0. Proses iterasi akan berakhir ketika selisih dari dua nilai x yang berurutan sangat kecil atau sama dengan nol seperti dinyatakan pada Persamaan (13) dan Persamaan (14). Andaikan proses iterasi berakhir pada saat i = n maka nilai xn adalah nilai maksimum dari x (xm). Nilai xm ini adalah merupakan nilai panjang gelombang maksimum (λm) dari persamaan kerapatan energi Uλ.
Rancangan flow chart dari metode Newton-Rapshon termodifikasi ditunjukkan pada Gambar 3.

Gambar 3. Diagram alir metode Newton-Rapshon termodifikasi.
-
3.2 Pengimplementasian kode program (source code)
Diagram alir metode NR termodifikasi yang diperlihatkan pada Gambar 3 selanjutnya diimplementasikan ke dalam kode program. Bahasa pemrograman yang dipakai yaitu Python Anaconda 3 Jupiter Notebook [11]. Bahasa Python sangat cocok dipakai untuk menangani data dimensi tinggi (matrik) seperti kasus penyelesaian metode NR termodifikasi. Disamping itu file master software Python Anaconda bisa diunduh secara gratis (open source) lewat halaman web resminya (www.anaconda.com). Spesifikasi komputer atau laptop pada penelitian ini yaitu laptop HP intel core i7 @1,30 GHz 4 cores dengan RAM 16 GB. Potongan kode program Python dari metode NR termodifikasi dapat dilihat pada kode program berikut ini. Kode program lengkap bisa diperoleh dengan menghubungi penulis lewat e-mail.
import matplotlib.pyplot as plt
import numpy as np import math
N=10000
x=np.empty((N),dtype=float)
x1=np.empty((N,dtype=float) y=np.empty((N),dtype=float) y1=np.empty((N),dtype=float) eps=1e-7 #1e-5
y[0] = float(input('Masukkan nilai awal(λ0) = ')) # 2e-6
n=0
selisih = 10
h=1e-10 #0.0001e-6
hp=6.6261e-34 #konstanta Planck
c=2.99e+8 #kecepatan cahaya
k=1.38e-23 #konstanta Boltzman
T=1800
while selisih >= eps:
n=n+1
x=y[n-1]
#fungsi berikut (fx dan dx) dpt berubah sesuai kasus
#*****************************
fxi = ((8*np.pi*hp*c)/(x**5)) * 1 / (np.exp ((hp*c) /((k*T)*x))-1)
fxi_plus_h=((8*np.pi*hp*c)/((x+h)**5)) * 1 / (np.exp ((hp*c) /((k*T)*(x+h)))-1)
fxi_min_h =((8*np.pi*hp*c)/((x-h)**5)) * 1 / (np.exp ((hp*c) /((k*T)*(x-h)))-1)
fx=(h/2)*(fxi_plus_h-fxi_min_h)/(fxi_plus_h-2*fxi+fxi_min_h)
#***************************
y[n]=x-fx #pers. Metode Newton-Rapshon orde-1
selisih=abs(y[n]-x) #selisih 2 nilai iterasi yg berurutan
print('λmax = %.11f'%(y[n]));
y_anal=0.002898/T
nilai_awal=1e-7
nilai_akhir=50e-7
interval=(nilai_akhir-nilai_awal)/100
x1=np.arange(nilai_awal,nilai_akhir,interval)
y1= ((8*np.pi*hp*c)/(x1**5)) * 1 / (np.exp ((hp*c) /(k*T*x1))-1)
plt.plot(x1,y1,'k')
plt.legend(['1800 K'])
plt.xlabel('λ (m)')
plt.ylabel('U(λ) ( J / m\u00b3 )')
Hasil eksekusi dari program NR termodifikasi untuk menentukan panjang gelombang maksimum (λm) dari persamaan kerapatan energi Uλ pada temperatur 1800 K ditampilkan pada Gambar 4. Dengan memberikan nilai awal (λ0) sebesar 2e-6 m (2x10-6 m) dan Temperatur (T) 1800 K maka diperoleh panjang gelombang maksimum (λmax) yaitu 0,00000160290 m (1,6029x10-6 m).
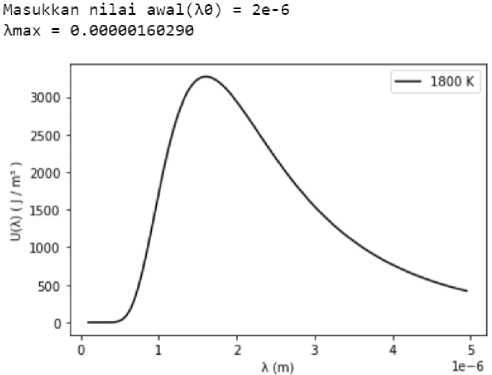
Gambar 4. Rapat energi U sebagai fungsi λ pada suhu T=1800 K menggunakan NR temodifikasi.
Sedangkan hasil perhitungan λm secara analitik dengan hukum pergeseran Wien untuk T = 1800 K dapat ditentukan dengan menggunakan Persamaan (10):
λm
2,898x10-3
1800
= 0,00000161000 = 1,6100x10-6 m
Hasil program NR termodifikasi untuk beberapa nilai temperatur yaitu: 1000 K, 1200 K, 1400 K, 1600 K, dan 1800 K diperlihatkan pada Gambar 5.
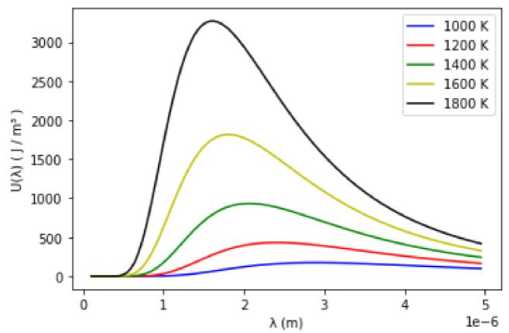
Gambar 5. Panjang gelombang maksimum (λm) untuk beberapa nilai T.
Data hasil perhitungan λm secara analitik (hukum pergeseran Wien) dan hasil perhitungan secara numerik (program Newton-Rapshon termodifikasi) dapat dilihat pada Tabel 1.
Tabel 1. Hasil perhitungan λm secara analitik dan NR termodifikasi.
|
Temperatur (K) |
Panjang gelombang maksimum λm (m) | |
|
Numerik (NR Termodifikasi) |
Analitik (Hukum Pergeseran Wien) | |
|
1000 |
2,8881x10-6 |
2,8980 x10-6 |
|
1200 |
2,4056x10-6 |
2,4150 x10-6 |
|
1400 |
2,0615 x10-6 |
2,0700 x10-6 |
|
1600 |
1,8033 x10-6 |
1,8113 x10-6 |
|
1800 |
1,6029 x10-6 |
1,6100 x10-6 |
Hasil regresi antara panjang gelombang max λm yang dihasilkan secara analitik (hukum pergerseran Wien) dengan panjang gelombang max λm yang dihasilkan secara numerik (Newton-Rapshon Termodifikasi) diperlihatkan pada Gambar 6.
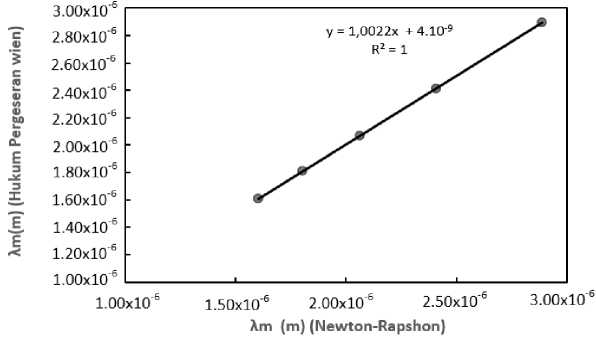
Gambar 6. Hasil regresi perhitungan panjang gelombang maksimum λm.
-
4.2 Pembahasan
Pada Gambar 5 bisa dilihat bahwa semakin tinggi temperatur T, maka nilai λm akan semakin kecil. Nilai λm akan bergeser semakin ke kiri. Hal ini sesuai dengan hukum pergeseran Wien yaitu jika temperatur semakin tinggi maka panjang gelombang maksimum semakin kecil. Temperatur T dan panjang gelombang maksimum λm mempunyai hubungan terbalik seperti dinyatakan pada Persamaan (22).
Untuk melihat tingkat kelinieran dari kedua metode tersebut maka dilakukan regresi linear antara λm hasil analitik (hukum pergeseran Wien) dengan λm yang dihasilkan secara numerik (Newton-Rapshon Termodifikasi) dengan menggunakan data pada Tabel 1. Regresi linear akan menghasilkan persamaan garis linear y = mx + c. Dimana m adalah gradien dan c adalah titik potong garis pada sumbu y (intercept) [12]. Pada Gambar 6 diperlihatkan bahwa hasil regresi linear yaitu persamaan garis y = 1,0022x + 4x10-9. Dimana gradien garis (m) =1,0022, nilai konstanta (c) = 4x10-9 dan koefisien determinasi R2 = 1. Hal ini menunjukkan bahwa nilai m, c dan R2 mendekati atau sama dengan nilai ideal. Nilai ideal dari gradien (m), konstanta (c) dan R2, secara berurutan, adalah 1, 0, dan 1. Jadi dapat dinyatakan bahwa nilai λm hasil perhitungan metode NR termodifikasi sangat mendekati hasil perhitungan analitik (hukum pergeseran Wien)
Metode NR termodifikasi terbukti bisa dipergunakan untuk menghitung panjang gelombang maksimum λm pada hukum pergeseran Wien. Hasil perhitungan panjang gelombang maksimum λm secara analitik dengan hukum Wien sangat mendekati hasil perhitungan secara numerik dengan metode Newton-Rapshon termodifikasi. Hal ini ditunjukkan oleh hasil regresi menghasilkan kurva linear dengan nilai gradien, konstanta dan koefisien determinasi yang mendekati nilai ideal. Sebagai perbandingan penentuan λm secara numerik bisa dicoba dengan metode lain seperti: Secant, Brent, Steffenson, Muller, Ridder dan lain-lain.
Ucapan Terima Kasih
Penulis mengucapkan terima kasih kepada Kepala Laboratorium Komputasi, Program Studi Fisika, FMIPA, UNUD, Badung, Bali yang telah menyediakan fasilitas dalam penelitian ini. Begitu pula seluruh rekan dosen Program Studi Fisika, FMIPA, UNUD atas semua masukan atau saran yang berhubungan dengan riset ini.
Pustaka
-
[1] A. Beiser, Concept of Modern Physics, sixth edition, McGraw-Hill Company, New York, USA, 2003.
-
[2] S.Weinberg, Foundations of Modern Physics, Cambridge University press, New York, USA, 2021.
-
[3] S. Gupta, Blackbody Radiation, Indian Institute of Science, Bangalore India, 2003.
-
[4] K. Dharmawan, L.P.I. Harini, Perbandingan Keefisienan Metode Newton-Rapshon, Metode Secant, dan Metode Bisection dalam Mengestimasi Implied Volatilitas Saham, E-Journal Matematika, vol.5, no.1, 2016.
-
[5] N.N.R. Utami, I N. Widana, N.M. Asih, Perbandingan Solusi Sistem Persamaan Nonlinear menggunakan Metode Newton-Rapshon dan Metode Jacobian, E-Journal Matematika, vol.2, no.2, 2013.
-
[6] R. Munir, Metode Numerik, Teknik Informatika, ITB, Bandung, 2005.
-
[7] K.S. Krane, Modern Physics, fourth edition, John Willey and Sons, Inc., New Jersey, USA, 2020.
-
[8] E. Bose, Wien's displacement law from Planck's law of radiation, Available from:
https://www.youtube.com/watch?v=AxGzVA3syDQ, diakses 2 Mei 2023.
-
[9] A. Das, Derivation of Wien's Displacement Law from Planck's Radiation Law, Available from: https://www.youtube.com/watch?v=h92gy1oKnAE, diakses 18 Mei 2023.
-
[10] R. Soegeng, Komputasi Numerik dengan Turbo Pascal, Penerbit Andi, Jogyakarta, 1993.
-
[11] D.J. Pine, Introduction to Python for Science and Engineering, CRC press, New York, USA, 2019.
-
[12] D.C. Montgomery, E.A. Peck, G.G. Vining, Introduction to Linear Regression Analysis, sixth edition, John Wiley & Sons, Inc., New Jersey, USA, 2021.
SINTA 4 Accreditation Starting on Volume 19 No. 2, 2018
161
Discussion and feedback