Studi Kestabilan Tegangan Jaringan IEEE 9 Bus Menggunakan Indeks Kestabilan Tegangan
on
A-009
Prosiding Conference on Smart-Green Technology in Electrical and Information Systems
Bali, 14-15 November 2013
Studi Kestabilan Tegangan Jaringan IEEE 9 Bus Menggunakan Indeks Kestabilan Tegangan
Avrin Nur Widiastuti, Lesnanto Multa Putranto, Randhy Ramono Syamri
Jurusan Teknik Elektro dan Teknologi Informasi
Fakultas Teknik UGM
Yogyakarta, Indonesia
Intisari — Sistem tenaga yang sangat terbebani sering terkendala oleh ketidakstabilan tegangan.Ketidakstabilan tegangan dapat menimbulkan banyak masalah, seperti jatuhnya tegangan pada sebagian besar sistem, keruntuhan tegangan (voltage collapse), bahkan potensi terjadinya blackout pada sistem.Pada penelitian ini simulasi berbasis waktu digunakan untuk mempelajari kestabilan tegangan sistem IEEE 9 bus. Penelitian ini menggunakan Indeks Kestabilan Tegangan (Voltage Stability Indeks, VSI) yang bertujuan untuk mengetahui tingkat kestabilan tegangan, memprediksi kapan terjadinya ketidakstabilan tegangan, dan mengetahui bagian sistem yang paling berpartisipasi atau rawanterhadap ketidakstabilan tegangan. Pada penelitian ini akan digunakan dua jenis indeks yaitu analisis modal dan PQVSI. Analisis modal menilai kestabilan tegangan dari eigenvalue matriks Jacobian tereduksi. Informasi dari eigenvektor matriks Jacobian tereduksi digunakan untuk mencari bus yang paling berpartisipasi terhadap kondisi ketidakstabilan tegangan yang dikenal dengan metodeFaktor Partisipasi Bus (FPB). Sedangkan PQVSI menilai kestabilan tegangan dengan membandingkan aliran daya suatu saluran pada waktu tertentu dengan batas aliran daya maksimalnya.Simulasi dilakukan dengan menggunakan 2 skenario. Skenario 1 dengan pemberian kenaikan beban sebesar 0,3 pu/detik pada bus 5. Hasil yang didapatkan system mulai menuju ketidakstabilan pada detik ke 12,83 yang ditandai dengan nilai eigenvalue mendekati nol (0,0121). Dengan FPB diketahui bahwa partisipasi terbesar adalah pada bus 5 dengan nilai 0,693.Dari analisis PQVSI didapatkan bahwa saluran dari bus 4 ke bus 5 merupakan saluran yang paling rawan menuju ketidakstabilan. Skenario 2 dengan pemberian kenaikan beban sebesar 2 pu pada bus 7. Hasil yang didapatkan system mulai menuju ketidakstabilan pada detik ke 23,92 yang ditandai dengan nilai eigenvalue mendekati nol (0,0013). Dengan FPB diketahui bahwa partisipasi terbesar adalah pada bus 7 dengan nilai 0,598.Dari analisis PQVSI diketahui bahwa saluran dari bus 7 ke bus 8 merupakan saluran yang paling rawan menuju ketidakstabilan.
Kata kunci— Kestabilan tegangan, ketidakstabilan tegangan, indeks kestabilan tegangan, analisis modal, faktor partisipasi bus, PQVSI.
-
I. PENDAHULUAN
Kestabilan tegangan kini memperoleh perhatian lebih karena pesatnya perkembangan beban membuat sistem Semakinterbebani [1]. Kestabilan tegangan adalah
kemampuan sistem untuk menjaga tegangan sistem pada seluruh bus tetap berada dalam batas kestabilan saat kondisi normal atau setelah terjadi gangguan.[2]
Ketidakstabilan tegangan dapat terjadi karena adanya gangguan, baik gangguan kecil berupa peningkatan pembebanan ataupun gangguan besar seperti lepasnya unit pembangkit besar atau perubahan permintaan daya dalam jumlah yang besar.Ketidakstabilan tegangan dapat mengakibatkan keruntuhan tegangan, profil tegangan yang sangat rendah disebagian besar sistem yang berpotensi menimbulkan blackout pada sistem.
Pendekatan statis lebih dipilih karena memiliki kelebihan-kelebihan seperti mampu memberikan informasi tentang tingkat kestabilan tegangan sistem, jarak kondisi sistem dengan batas wilayah ketidakstabilan tegangan, serta mampu menginformasikan bus atau saluran yang menjadi penyebab sistem memasuki wilayah ketidakstabilan tegangan.Salah satu metode yang digunakan pada pendekatan statis adalah menggunakan indeks kestabilan tegangan (VSI). Indeks kestabilan tegangan terdiri atas dua jenis, yaitu berbasis bus dan berbasis saluran.
-
II. KRITERIA KESTABILAN TEGANGAN
-
i. Kurva P-V
Kurva P-V diperoleh dengan cara melakukan simulasi aliran daya dimana beban mengalami perubahan. Simulasi ini akan menghasilkan nilai-nilai magnitude tegangan dan daya aktif pada suatu bus yang senantiasa berubah membentuk sebuah kurva yang berbentuk ‘hidung (nose)’. Titik balik dari kurva P-V merupakan titik kritis pembebanan atau titik pembebanan maksimum seperti yang diperlihatkan pada Gambar 1.Wilayah di atas titik kritis merupakan wilayah operasi yang masih stabil dan wilayah di bawah titik kritis merupakan wilayah operasi yang tidak stabil.
-
ii. Kurva Q-V [3]
Kurva Q-V masih banyak digunakan perancang sistem tenaga dalam menganalisa kriteria kinerja system, karena kurva ini mampu meminformasikan sensitivitas dan variasi pengaruh injeksi daya reaktif terhadap tegangan bus.Kestabilan tegangan sistem dapat diketahui dari
hubungan antara injeksi daya reaktif dan tegangan pada suatu bus.Sistem tidak stabil, saat tegangan (V) suatu bus menurun saat injeksi daya reaktif (Q) ke bus tersebut ditingkatkan. Jadi, kestabilan tegangan tercipta saat sensitivitas V-Q bernilai positif dan ketidakstabilan tegangan ditandai dengan sensitivitas V-Q bernilai negatif minimal pada salah satu bus (Gambar 2). Pada sistem yang relatif besar, untuk mencari bus yang kritis harus dilakukan perhitungan kurva Q-V dalam jumlah yang besar.
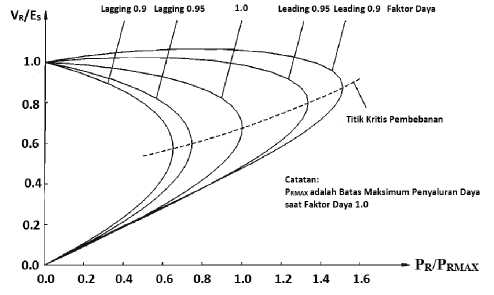
gbr. SEQ Gbr. \* ARABIC 1. kurva p-v [2]
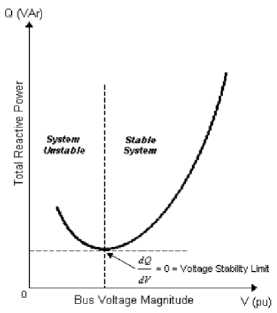
Gbr. 1. Kurva Q-V
-
III. ANALISIS SENSITIVITAS V-Q
sebaliknya bila ΔV /ΔQ bernilai negatif atau nol, sistem berada dalam kondisi ketidakstabilan tegangan.
Karakteristik kestabilan tegangan sistem bisa diidentifikasi dengan menghitung eigenvalue dan eigen vektor dari matriks Jacobian tereduksi sesuai persamaan (4)
J =ξΛη ↔Ј =ξΛ η (4)
dengan ξ = Matrix Eigenvektor kanan JR
η = Matrix Eigenvektor kiri JR
A = Matrix Eigenvalue diagonal JR
Subtitusi persamaan (4) ke persamaan (2) akan dan karenaξ-
-
1 = ηakan diperoleh (5)
1
v= λ q (5)
Kestabilan tegangan bisa diketahui dari mode eigenvalue λi. Eigenvalue minimum dari sistem merepresentasikan sensitivitas V-Q.Sistem stabil bila λI bernilai positif.Saat λI bernilai nol maka sistem berada di batas kestabilan tegangan.Sistem tidak stabil bila λI bernilai negatif.
-
V. FAKTOR PARTISIPASI BUS(FPB) [2]
Metode ini mampu memberikan informasi tentang
seefektif apa perubahan daya reaktif pada suatu bus dapat
memberi perubahan pada tegangan pada bus tersebut. Hal
ini diperoleh dari
P =ξ η
(6)
Faktor partispasi bus menjelaskan besar kontribusi perubahan pada sebuah bus terhadap kondisi kestabilan tegangan sistem.Oleh karena itu, faktor partisipasi bus dapat digunakan untuk mencari bus yang rawan menuju ketidakstabilan tegangan atau bus penyebab ketidakstabilan tegangan. Bus yang paling berpartisipasi akan memiliki nilai faktor partisipasi bus terbesar.
Dari persamaan aliran daya metode Newton-Rahphson dapat diperoleh matriks Jacobian.Persamaan (1) merepresentasikan model linierisasi dari sistem tenaga pada kondisi operasi tertentu.
ΔP = J θ Ϳ Δθ
ΔQ J θ Ϳ ΔV
denganΔΡ = 0 akan diperoleh persamaan (2)
ΔV=J ΔQ
(1)
(2)
VI. PQ VOLTAGE STABILITY INDEX (PQVSI) [5]
Indeks kestabilan tegangan berbasis saluran yang menilai kestabilan tegangan dari perbandingan besar aliran
JR=[JQV - JQθ JPθ-1 JPV]
(3)
daya aktif pada suatu saluran pada suatu kondisi dengan batas maksimal penyaluran daya pada tersebut. Batas maksimal penyaluran daya sebuah diperoleh dari persamaan berikut
|V |
P = 2Im(АВ∗)tanθ -2Re(АВ∗)+2|A||B|secθ
operasi saluran saluran
(7)
dengan JRadalah matriks Jacobian tereduksi. MatriksJR-1adalah sensitivitas V-Q mempelihatkan hubungan ΔԚdan ΔV. Bila ΔV /ΔQ bernilai positif maka sistem stabil dan
dengan
A = 1+ZY
B = Ζ
θ = Sudut aliran daya
Sistem diasumsikan denganmenggunakan model saluran π seperti Gambar 3.
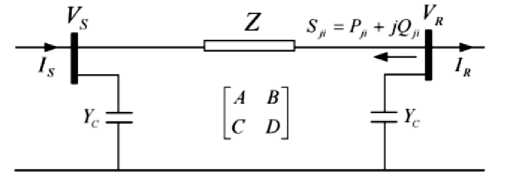
Gbr. 3. Model π saluran transmisi
Gambar 4 memperlihatkan hubungan penyaluran daya
operasi tertentu dengan titik operasi saat keruntuhan
kestabilan tegangan.Kestabilan sistem dapat dengan persamaan berikut :
OA P
VSI ij=OB=PNP,0 ≤VSIij ≤1
PQVSI = ( VSIij )
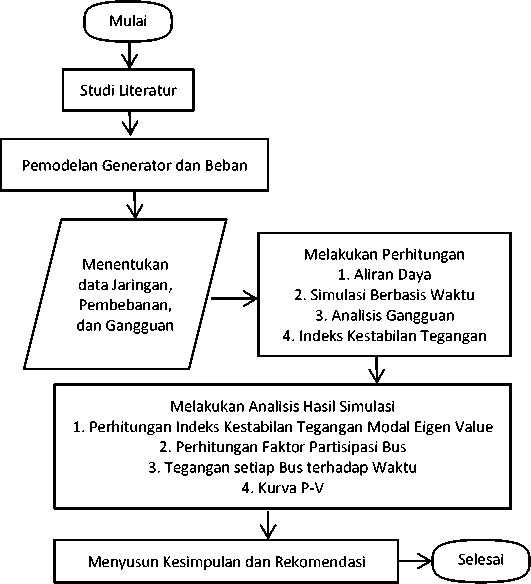
Gbr. 5. Diagram Alir Penelitian
diketahui
(8)
(9)
dengan
P adalah aliran daya aktif dari bus j ke bus i
P ji adalah aliran daya maksimal suatu saluran
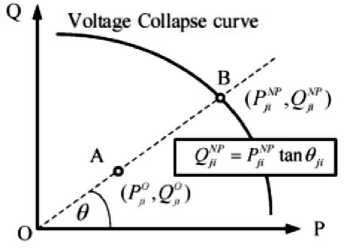
Gbr. 4. Kurva P-Q saat Titik Keruntuhan Kestabilan Tegangan
Indeks kestabilan tegangan PQVSI akan bernilai0 ≤ VSI≤1. Sebuah saluran akan dikatakan rawan menuju ketidakstabilan tegangan saat nilai PQVSI bernilai mendekati 1.
-
VII. METODOLOGI PENELITIAN
Penelitian ini menggunakan software MATLAB dengan toolbox Matpower dan Simulink.Objek penelitian ini adalah sistem IEEE 9 Bus.Gambar 5 di bawah ini menjelaskan tentang alur prosedur penelitian ini. Penelitan dilakukan dengan 2 skenario dan setiap skenario mengikuti alur seperti dalam Gambar 5.
-
VIII. PEMODELAN
Penelitian ini menggunakan sistem IEEE 9 bus seperti dalam Gambar 6sebagai berikut :
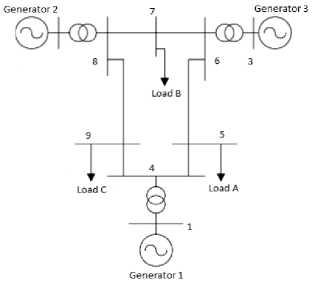
Gbr.6. Sistem IEEE 9 bus
Generator dimodelkan menggunakan model 4 statesebagai berikut :
|
Е′̇ d |
1 = f (-Е'd Т qo |
+(Lq-L′q)іq) |
(10) |
|
Е′̇ q |
1 =Тf (-Е q Т |
-(Ld-L′d)іd+Εfd ) |
(11) |
|
1 |
(12) | ||
|
Δω |
= (Т mech |
-Тem-D. Δω ) | |
|
■ δ̇ = |
ωr,base . Δω |
(13) |
-
IX. HASIL DAN PEMBAHASAN
Adapun skenario gangguan yang dilakukan dalam penelitian ini adalah sebagai berikut
-
1. Gangguan kecil pada bus 5 dengan slope 0.3 pu per detik sejak detik ke1
-
2. Terjadi gangguan besar pada bus7 dengan kenaikan beban 2 pu pada detik ke1
-
i. Hasil Skenario 1
Tabel 1 menginformasikan tingkat kestabilan tegangan sistem dari waktu ke waktu dan dapat kita lihat pada detik ke13 eigenvalue ke3 bernilai negatif.Hal ini menandakan sistem telahkehilangan kestabilan tegangannya.Gambar 7 memperlihatkan sistem menuju kondisi ketidakstabilan pada detik ke12.83.
Tabel 1- Matriks Eigenvalue Skenario 1
|
Eigen ke |
Detik 4 |
Detik 8 |
Detik 12 |
Detik 12.83 |
Detik 13 | |||
|
Eig ke-1 |
48.8066 |
46.7591 |
40.8642 |
38.0210 |
37.2841 | |||
|
Eig ke-2 |
44.5434 |
42.5952 |
36.8481 |
34.1069 |
33.4186 | |||
|
Eig ke-3 |
34.7625 |
33.1354 |
2.0638 |
0.0121 |
-0.6217 | |||
|
Eig ke-4 |
5.5394 |
4.8516 |
11.2573 |
25.8171 |
10.117 | |||
|
Eig ke-5 |
12.2645 |
11.4246 |
8.9504 |
10.3466 |
7.5285 | |||
|
Eig ke-6 |
14.0730 |
13.2794 |
28.3207 |
7.8100 |
25.1401 | |||
|
6 5 4 (D 3 ra S 3 E? Lu E I2 S 1 0 -1 0 |
468 Time (s) |
X: 12 Y: -0. 10 12 1 |
.83 001739 4 | |||||
Gbr. 7 Kurva perubahan eigenvalue mode 3 skenario 1
Tabel 2 - Faktor Partisipasi Bus Detik ke-12.83
|
Bus ke |
Eig 1 |
Eig 2 |
Eig 3 |
Eig 4 |
Eig 5 |
Eig 6 |
|
Bus 4 |
0.186 |
0.598 |
0.141 |
0.074 |
0.001 |
0.000 |
|
Bus 5 |
0.025 |
0.054 |
0.693 |
0.038 |
0.157 |
0.033 |
|
Bus 6 |
0.067 |
0.020 |
0.042 |
0.111 |
0.035 |
0.724 |
|
Bus 7 |
0.199 |
0.104 |
0.024 |
0.234 |
0.408 |
0.032 |
|
Bus 8 |
0.436 |
0.161 |
0.012 |
0.009 |
0.198 |
0.184 |
|
Bus 9 |
0.087 |
0.064 |
0.087 |
0.534 |
0.201 |
0.027 |
Eigenvalue terendah pada skenario 1 berada pada eigenvalue mode ke3.Faktor partisipasi bus dilakukan saat eigenvalue mendekati 0 yaitu pada detik ke12.83 yang
bernilai 0.0121.Bus yang memiliki nilai partisipasi terbesar pada mode eigenvalue ke3 adalah bus 5, bernilai 0.693.Hal ini menandakan bus yang paling berpartisipasi (mengalami gangguan) pada skenario 1 adalah bus 5.
Gambar 8 merupakan kurva P-V bus 5 skenario 1. Titik pembebanan maksimum atau titik kritis bus 5 skenario 1 terjadi pembebanan sebesar 387.9 MW dan jatuh tegangan ke 0.6744 pu yang terjadi pada detik ke 12.24 sesuai Gambar 9.
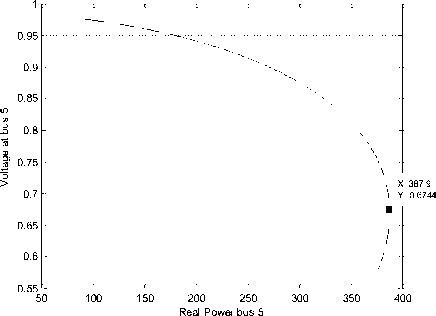
Gbr. 8 Kurva P-V Bus 5 Skenario 1
Gambar 9juga memperlihatkan profil tegangan bus beban pada skenario 1.Dapat dilihat tegangan bus 5, bus yang mengalami gangguan, memiliki profil tegangan terendah.
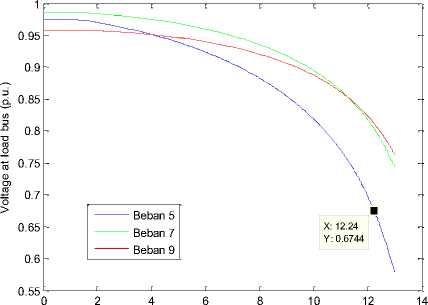
Time (s)
Gbr. 9 Kurva profil tegangan bus beban skenario 1
Tabel 3 memperlihatkan perbandingan aliran daya suatu saluran pada detik tertentu terhadap batas maksimum penyalurannya.Saluran yang paling rawan pada skenario 1 adalah saluran dari bus 4 ke bus 5, dimana pada detik 13 PQVSI bernilai 0.976 yang merupakan nilai maksimal pembebanan.Indeks ini mampu memperlihatkan perkembangan tingkat kestabilan tegangan berbasis saluran sehingga dapat diprediksi batas penyaluran yang tidak mengganggu kestabilan tegangan sistem.
Tabel 3 - PQVSI Skenario 1
|
Saluran |
Detik ke4 |
Detik ke8 |
Detik ke12 |
Detik ke13 |
|
1 - 4 |
0.2162 |
0.4033 |
0.6849 |
0.7873 |
|
4 - 5 |
0.2614 |
0.5167 |
0.8699 |
0.9760 |
|
5 - 6 |
0.3633 |
0.4745 |
0.7199 |
0.8617 |
|
3 - 6 |
0.0962 |
0.1131 |
0.1762 |
0.2342 |
|
6 - 7 |
0.1009 |
0.0197 |
0.1323 |
0.2099 |
|
7 - 8 |
0.1631 |
0.2108 |
0.3202 |
0.3897 |
|
8 - 2 |
0.2073 |
0.2309 |
0.3128 |
0.3759 |
|
8 - 9 |
0.3471 |
0.3135 |
0.2991 |
0.3211 |
|
9 - 4 |
0.1765 |
0.2047 |
0.2664 |
0.2960 |
-
ii. Hasil Skenario 2
Tabel 4 merupakan nilai eigenvalue dari matriks Jacobian tereduksi sistem. Tabel ini memperlihatkan sistem dapat bertahan dari kenaikan sebesar 2 pu sampai detik ke23. Mode minimum saat ketidakstabilan muncul adalah mode eigenvalue ke2. Gambar 10 memperlihatkan sistem mulai tidak stabil sejak detik ke23.92
Tabel 4 - Matriks Eigenvalue Skenario 2
|
Eigen ke |
Detik 15 |
Detik 20 |
Detik 23 |
Detik 23.92 |
Detik 24 |
|
Eig ke-1 |
43.2336 |
41.6711 |
39.4262 |
37.3881 |
36.9879 |
|
Eig ke-2 |
36.2382 |
32.6271 |
26.0823 |
0.0013 |
-0.3734 |
|
Eig ke-3 |
27.9109 |
25.3057 |
20.8416 |
5.5579 |
5.378 |
|
Eig ke-4 |
4.1893 |
3.5941 |
2.1409 |
8.7243 |
17.6144 |
|
Eig ke-5 |
9.3047 |
8.2732 |
6.6876 |
18.8374 |
15.1841 |
|
Eig ke-6 |
12.4048 |
11.6968 |
10.4473 |
16.0732 |
8.3128 |
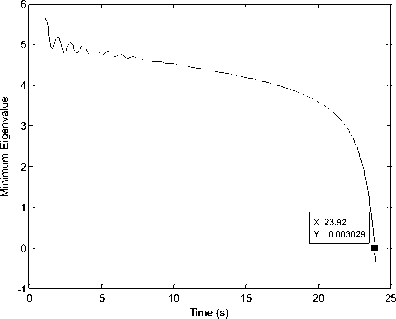
Gbr. 10 Kurva perubahan eigenvalue mode 2 skenario 2
Tabel 5 – Faktor Partisipasi Bus Detik ke23.92
|
Bus ke |
Eig 1 |
Eig 2 |
Eig 3 |
Eig 4 |
Eig 5 |
Eig 6 |
|
Bus 4 |
0.824 |
0.012 |
0.146 |
0.001 |
0.018 |
0.000 |
|
Bus 5 |
0.080 |
0.030 |
0.386 |
0.339 |
0.012 |
0.152 |
|
Bus 6 |
0.002 |
0.089 |
0.002 |
0.170 |
0.360 |
0.377 |
|
Bus 7 |
0.000 |
0.598 |
0.125 |
0.010 |
0.260 |
0.007 |
|
Bus 8 |
0.002 |
0.220 |
0.002 |
0.115 |
0.338 |
0.322 |
|
Bus 9 |
0.092 |
0.052 |
0.339 |
0.365 |
0.011 |
0.141 |
Eigenvalue terendah skenario 2 berada pada mode eigenvalue ke3.FPB dilakukan saat eigenvalue mendekati nilai 0, yaitu pada detik ke23.92 bernilai 0.0013.Bus yang memiliki nilai partisipasi terbesar pada mode eigenvalue ke-2 adalah bus 7 sebesar 0.598.Hal ini menandakan bus yang paling berpartisipasi (mengalami gangguan) pada skenario 1 adalah bus 7.
Tabel 6 merupakan hasil dari analisis PQVSI yang menunjukkan perbandingan aliran daya suatu saluran pada detik tertentu terhadap batas maksimum penyalurannya.Saluran yang paling rawan pada skenario 2 adalah saluran dari bus 7 ke bus 8, pada detik ke 24 yang memiliki nilai PQVSI bernilai 0.9073.Indeks ini mampu memperlihatkan perkembangan tingkat kestabilan tegangan berbasis saluran sehingga dapat diprediksi batas penyaluran yang tidak mengganggu kestabilan tegangan sistem.
Tabel 6 – PQVSI Skenario 2
|
Saluran |
detik ke15 |
detik ke20 |
detik ke23 |
detik ke24 |
|
1 - 4 |
0.4686 |
0.5216 |
0.5914 |
0.6591 |
|
4 - 5 |
0.4089 |
0.4659 |
0.5508 |
0.6369 |
|
5 - 6 |
0.385 |
0.4974 |
0.6892 |
0.0408 |
|
3 - 6 |
0.151 |
0.1791 |
0.2555 |
0.3984 |
|
6 - 7 |
0.4632 |
0.5493 |
0.7187 |
0.8915 |
|
7 - 8 |
0.4773 |
0.5653 |
0.7394 |
0.9073 |
|
8 - 2 |
0.3273 |
0.389 |
0.545 |
0.8163 |
|
8 - 9 |
0.3215 |
0.4494 |
0.0004 |
0.1742 |
|
9 - 4 |
0.4515 |
0.5081 |
0.5934 |
0.7019 |
-
X. KESIMPULAN
Pada penelitian ini telah dibahas kestabilan tegangan pada sistem tenaga dan metode analisis yang efektif dalam memperoleh informasi penting tentang kestabilan tegangan sebuah sistem tenaga listrik.Indeks kestabilan tegangan dengan modal eigenvalue dan PQVSI merupakan metode yang digunakan pada penelitian ini.Kedua metode ini mampu memberikan informasi penting tentang kestabilan tegangan, seperti tingkat kestabilan tegangan, jarak kondisi
operasi dengan batas operasi yang masih stabil, dan bagian dari sistem yang menjadi penyebab ketidakstabilan tegangan sistem.
Pada skenario 1 dapat diketahui bahwa sistem mampu menjaga kestabilannya hingga detik ke12.83 dan mode eigenvalue terendah berada pada mode ke 3 dengan nilai 0.0121. Pada skenario 1, bus yang memiliki partipasi terbesar adalah bus ke 5 sebesar 0.693, sehingga metode faktor partisipasi bus mampu mengetahui bus yang mengalami masalah.Analisis PQVSI mampu
memperlihatkan saluran paling rawan menuju kondisi ketidakstabilan adalah saluran dari bus ke 4 ke bus ke 5, dimana pada detik ke 13 nilai PQVSI bernilai 0.976.
Pada skenario 2 dapat diketahui bahwa sistem mampu menjaga kestabilannya hingga detik ke 23.92 dan mode eigenvalue terendah berada pada mode ke 2 dengan nilai 0.0013.Pada skenario 2, bus yang memiliki partipasi terbesar adalah bus ke 7 sebesar 0.598, sehingga metode faktor partisipasi bus mampu mengetahui bus yang mengalami masalah. Analisis PQVSI mampu memperlihatkan saluran yang paling rawan menuju kondisi ketidakstabilan adalah saluran dari bus ke 7 ke bus ke 8, dimana pada detik ke 24 nili PQVSI bernilai 0.9073.
DAFTAR PUSTAKA
-
[1] C. Sharma dan M. G. Ganes, "Determination of the Applicability of using Modal Analysis for the Prediction of Voltage Stability," in Transmission and Distribution Conference and Exposition, 2008.
-
[2] Prabha Kundur, Power System Stability and Control. New York, USA: McGraw-Hill, 1994.
-
[3] S. D. Naik, M. K. Khedkar, dan S. S. Bhat, "Correlation and Comparison between Bus Participation Factor and Voltage Sensitivity Factor for Simultaneous and Individual Bus Load Change in Multi Bus Power System," IEEE, 2011.
-
[4] B. Gao, G. K. Morison, dan P. Kundur, "Voltage Stability Evaluation using Modal Analysis," IEEE Transactions on Power Systems, pp. 7(4):p.14, 1992.
Expansion Planning with Consideration of Voltage Stability using Genetic Algorithm," in ECTI-CON 2011, Thailand, 2011, pp. 909-912.
-
[6] Lesnanto M. P., Naebboon, dan Hoonchareon, "Real Time Voltage Stability Prediction based on Modal Analysis for Supporting Wide Area Monitoring System," International Conference on Electrical, Electronics, and Civil Engineering (ICEECE 2011), pp. 208-212, December 2011.
-
[7] Qingsheng Li, Dongfang Zhang, dan Tao Xu, "Study on the Key Buses to Power System Steady-State Voltage Stability," 2nd International Conference on Electronic & Mechanical Engineering and Information Technology (EMEIT-2012), 2012.
42
ISBN: 978-602-7776-72-2 © Universitas Udayana 2013
Discussion and feedback