ANALISIS REGRESI LOGISTIK ORDINAL SPASIAL STATUS KETAHANAN PANGAN PADA KABUPATEN/KOTA DI INDONESIA TAHUN 2020
on
E-Jurnal Matematika Vol. 12(4), November 2023, pp. 281-288
DOI: https://doi.org/10.24843/MTK.2023.v12.i04.p430
ISSN: 2303-1751
ANALISIS REGRESI LOGISTIK ORDINAL SPASIAL STATUS KETAHANAN PANGAN PADA KABUPATEN/KOTA DI INDONESIA TAHUN 2020
Ni Nyoman Utami Dewi1, Made Susilawati2§, I Gusti Ayu Made Srinadi3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: utamidewi908@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]
§Corresponding Author
ABSTRACT
Food is a basic need which is a right for humans to survive and has an important role so that an arrangement is needed that describes the level of food security in each region. Food security status shows the food stability of a region in terms of availability, access, and consumption of food for the local populace. The diversity of regencies/cities gives a variance effect in the results of food security so that the spatial influence is included in modeling the status of food security owing to the likelihood of interactions in our research between regions with one another, meaning that the condition of food security in regencies/cities is influenced by the condition of neighboring regencies/cities. Based on this, a model is that may be utilized to assess the state of food security is required in districts/cities in Indonesia in 2020. Logistic regression analysis is one technique that may be utilized to create the model regression analysis. Logistic regression analysis is a regression method that tests whether there is a probability the independent variable has the ability to predict the dependent variable.
Keywords: Status of Food Security, Ordinal Logistics Regression Analysis, Spatial Analysis, Spatial Ordinal Logistics Regression Analysis Methods.
-
1. PENDAHULUAN
Musim hujan secara alami berdampak pada Indonesia karena posisi geografisnya. sehingga menimbulkan adanya musim hujan dan musim kemarau. Karena pertanian di Indonesia menghasilkan bahan pangan seperti jagung, beras, sayur-mayur, buah-buahan, karet, kopi, gula, tembakau, dan lain-lain dalam jumlah yang relatif besar, sangat bermanfaat bagi kemakmuran dan kelangsungan penduduk Indonesia di bidang pangan. Alhasil, musim-musim tersebut mampu menjadikan Indonesia sebagai negara agraris yang unggul. Pangan menjadi kebutuhan dasar yang merupakan hak bagi manusia atas kelangsungan hidupnya dan memiliki peranan penting sehingga diperlukannya suatu susunan yang menggambarkan tingkat ketahanan pangan pada setiap daerah. Status ketahanan pangan menunjukkan stabilitas pangan suatu wilayah baik dari akses penduduk wilayah, konsumsi, maupun ketersediaan pangan (Webb & Rogers,
2003). Untuk memperhitungkan pengaruh geografis ketika memperkirakan keadaan ketahanan pangan, berbagai kabupaten dan kota berkontribusi terhadap efek varians dalam hasil ketahanan pangan. pada penelitian ini disebabkan oleh kecenderungan adanya interaksi antar wilayah satu dengan lainnya artinya Geografis kabupaten dan kota terdekat berdampak pada tingkat ketahanan pangan di kabupaten atau kota tertentu.
Berdasarkan hal tersebut diperlukan suatu model untuk memprediksi keadaan ketahanan pangan di kabupaten dan kota di Indonesia pada tahun 2020. Analisis regresi logistik merupakan salah satu teknik yang dapat digunakan untuk membuat model ini (Ghozali, 2018;325). Ada tiga jenis analisis regresi logistik (Hosmer&Lemeshow, 2000): biner, multinomial, dan ordinal. Untuk mengetahui variabel-variabel yang memengaruhi tingkat ketahanan pangan dapat digunakan analisis regresi logistik. Untuk menilai tingkat ketahanan pangan kabupaten dan kota di
Indonesia tahun 2020, dapat digunakan analisis regresi logistik ordinal spasial. Diketahui pula bahwa status ketahanan pangan merupakan variabel dependen skala ordinal dengan lima kategori, yaitu kerawanan pangan tinggi, kerawanan pangan sedang, kerawanan pangan rendah, ketahanan pangan rendah, dan ketahanan pangan sedang.
Penelitian yang sejenis sudah pernah dilakukan oleh Trivanni, I A(2018) dengan hasil bahwa Rasio konsumsi normatif, persentase penduduk yang hidup dalam kemiskinan, persentase rumah tangga yang tidak memiliki akses air bersih, persentase balita yang pendek, angka harapan hidup, indeks pembangunan manusia, dan variabel spasial ketahanan pangan adalah faktor-faktor yang memengaruhi tingkat ketahanan pangan kabupaten/kota menurut analisis regresi logistik ordinal spasial.
Jenis Informasi yang digunakan dalam penelitian ini adalah data sekunder yang dikumpulkan dari beberapa organisasi baik offline maupun online. Penelitian ini menggunakan data yang telah dipublikasikan oleh instansi-instansi di antaranya Badan Pusat Statistika (BPS) setiap provinsi di Indonesia, Badan Ketahanan Pangan, Kementerian Pertanian, Kementerian Kesehatan, dan Dinas Pertanian.
Ada faktor dependen dan variabel independen yang digunakan dalam penelitian ini. Tabel berikut mencantumkan variabel-variabel yang digunakan dalam penelitian ini disajikan pada Tabel 1 dan 2.
Dalam penelitian ini, analisis deskriptif dan analisis regresi logistik ordinal spasial digunakan untuk menganalisis data. Aplikasi seperti Quantum-Gis, OpenGeoda, SPSS, dan Microsoft Excel digunakan untuk analisis data dalam pekerjaan ini. Kondisi masing-masing variabel dideskripsikan menggunakan analisis deskriptif dalam bentuk tabel dan diagram.
Kemudian, analisis regresi logistik ordinal spasial berupaya mengidentifikasi unsur-unsur yang mempengaruhi tingkat ketahanan pangan kabupaten dan kota di Indonesia pada tahun 2020.
Adapun langkah-langkah yang dilakukan untuk menganalisis ketahanan pangan pada kabupaten/kota di Indonesia tahun 2020 yaitu: 1. Diawali dengan studi Pustaka.
-
2. Menentukan rumusan masalah.
-
3. Menentukan variabel penelitian.
-
4. Setelah itu, mengumpulkan data dan
melakukan input data terkait indeks
ketahanan pangan (IKP) untuk menghasilkan pemetaan yang dan disesuaikan dengan cut off point menggunakan Quantum-Gis.
Tabel 1. Variabel Dependen
|
Variabel |
Definisi Operasional Variabel |
Skala/Kategori |
|
Variabel Dependen | ||
|
Status Ketahanan Pangan (Y) |
Status ketahanan pangan menunjukkan Ketahanan pangan di suatu daerah tergantung pada aksesibilitas, ketersediaan, dan konsumsinya bagi penduduk wilayah tersebut. Status ketahanan pangan terbagi atas 6 kategori, yaitu:
ketahanan diet yang tinggi |
Ordinal |
Tabel 2. Variabel Independen
|
Variabel Independen | ||
|
Produktivitas padi (X1) |
Produksi padi sebagai persentase luas lahan (ton/ha) |
Rasio |
|
Jumlah penduduk (X2) |
jumlah penduduk dan pengunjung kawasan tersebut. |
Rasio |
|
Laju pertumbuhan penduduk (X3) |
persentase yang mewakili peningkatan populasi tahunan selama periode waktu tertentu. |
Rasio |
|
Persentase penduduk miskin (X4) |
persentase penduduk yang pengeluaran per kapitanya di bawah garis kemiskinan. |
Rasio |
|
Persentase rumah tangga tanpa akses listrik (X5) |
persentase rumah tanpa akses listrik PLN atau non-PLN. |
Rasio |
|
Persentase rumah tangga tanpa akses air bersih (X6) |
proporsi rumah yang jaraknya kurang dari 10 meter dari fasilitas pengumpulan sampah atau kotoran dan memiliki akses ke meteran, ritel, sumur terlindung, mata air terlindung, dan curah hujan sebagai sumber air minum. |
Rasio |
|
Persentase balita gizi kurang dan stunting (X7) |
persentase anak kurang gizi di bawah usia lima tahun. |
Rasio |
|
Angka harapan hidup (X8) |
perkiraan rentang hidup neonatus, dengan asumsi tidak ada perubahan kematian. |
Rasio |
|
Indeks Pembangunan Manusia (X9) |
Harapan hidup, pendidikan, dan tingkat kehidupan yang terhormat semuanya termasuk dalam indeks komposit. |
Rasio |
|
Unsur Spasial (X10) |
Perkalian IKP dengan nilai pembobot spasial |
Rasio |
Tabel 2. Cut Off Point Ketahanan Pangan
|
Kelompok IKP |
Rataan Nilai IKP Kabupaten |
Rataan Nilai IKP Kota |
|
1 |
≤ 41,52 |
≤ 28,84 |
|
2 |
> 41,52 |
> 28,84 |
|
- 51,42 |
- 41,44 | |
|
3 |
> 51,42 |
> 41,44 |
|
- 59,58 |
- 51,29 | |
|
4 |
> 59,58 |
> 51,29 |
|
- 67,75 |
- 61,13 | |
|
5 |
> 67,75 |
> 61,13 |
|
- 75,68 |
- 70,64 | |
|
6 |
> 75,68 |
> 70,64 |
Sumber: Indeks Ketahanan Pangan BPKP 2020.
-
5. Melakukan analisis secara deskriptif pada pemetaan yang diperoleh.
-
6. Menentukan matriks pembobot spasial
berdasarkan pemetaan yang diperoleh menggunakan metode Queen Contiguity
-
7. Setelah itu, nilai pembobot spasial
dikalikan dengan nilai indeks ketahanan pangan yang telah diperoleh sebelumnya untuk memperoleh variabel penjelas (X10).
-
8. Selanjutnya melakukan uji efek spasial
yang terdiri atas Moran’s I dan Lagrange Multiplier (LM).
-
9. Langkah selanjutnya adalah
menggunakan analisis SAR untuk memastikan interaksi antara faktor independen dan variabel dependen menggunakan OpenGeoda untuk
memperoleh model SAR.
-
10. Model SAR yang diperoleh, yaitu Uji G (uji Simultan), Uji kecocokan model keseluruhan, dan Uji Wald.
-
11. Kemudian dilakukan pemeriksaan kesesuaian model SAR menggunakan Nagelkerke R, dan AIC.
-
12. Langkah terakhir yang dilakukan adalah melakukan interpretasi model dan kesimpulan yang didapat.
-
3. HASIL DAN PEMBAHASAN
Adapun peta statusnketahanan pangan yang dihasilkan dengan menggunakan software Open Geoda ditampilkannpada gambarndi bawah ini.
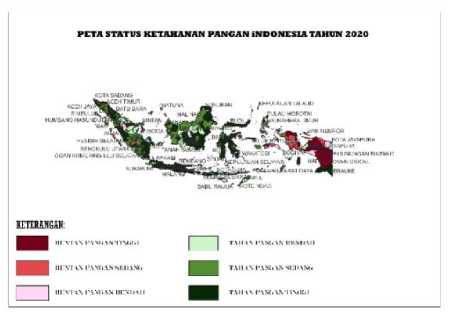
Gambar 1. Peta Status Ketahanan Pangan dengan Label
Berdasarkan peta status ketahanan pangan di atas, terlihat bahwa dari 514 kabupaten dan kota yang ada Indonesia pada perkiraan tahun 2020 membentuk kelompok-kelompok yang menggambarkan status ketahanan pangan sesuai dengan tingkat ketahanan pangan menurut publikasi Dewan Ketahanan Pangan. Kerawanan pangan tinggi, kerawanan pangan sedang, kerawanan pangan rendah, ketahanan pangan rendah, dan ketahanan pangan sedang adalah lima pengelompokan tingkat ketahanan pangan. Sebanyak 270 kabupaten dan kota masuk ke dalam kelompok keenam pada status ketahanan pangan yang ditandai dengan warna hijau tua, artinya 270 kabupaten dan kota tersebut memiliki tingkat ketahanan pangan tinggi sehingga diketahui kabupaten dan kota tersebut mampu memenuhi kebutuhan penduduk di wilayahnya berdasarkan aspek ketersediaan, aspek keterjangkauan, dan aspek pemanfaatan pangan.
Kemudian terdapat 115 kabupaten dan kota yang merupakan kelompok kelima status ketahanan pangan yang ditandai dengan warna hijau, artinya bahwa 115 kabupaten dan kota tersebut memiliki ketahanan pangan sedang. Selain itu, terdapat pula 53 kabupaten dan kota yang wilayahnya diberi warna hijau pucat yang berarti wilayah tersebut merupakan wilayah yang memiliki status ketahanan pangan, yaitu tahannpangan rendah.
Ada 28 kabupaten dan kota di Indonesia, dan daerah berwarna merah muda adalah daerah dengan kerentanan pangan minimal. Kemudian warna merah muda melambangkan kabupaten dan kota yang termasuk ke dalam kelompok kedua status ketahanan pangan, artinya kabupaten dan kota tersebut merupakan daerah dengan status ketahanan
pangan yaitu rentan pangan sedang sejumlah 20 kabupaten dan kota. Selanjutnya terdapat 28 kabupaten dan kota yang wilayahnya diberi warna merah tua yang artinya daerah tersebut merupakan daerah dengan rentan pangan tinggi. Dari gambaran tersebut terlihat ada pola spasial pada data status ketahanan pangan di Kabupaten/Kota di Indonesia. Menurut Lee dan Wong (2001), pola spasial adalah sesuatu yang menunjukkan penempatan atau susunan benda-benda di permukaan bumi. Ward dan Gleditsch (2008) menyatakan bahwa ketergantungan spasial pada sebuah analisis dapat dibentuk dalam sebuah matriks pembobot spasial.
Analisis data pada kasus ini diperoleh dengan bantuan software Open Geoda dan SPSS.
-
a. Uji Efek Spasial
Dalam kasus ini menggunakan dua uji efek spasial, yaitu Moran’s I dan Lagrange Multiplier (lag).
-
1) Moran’s I
Hipotesis:
H0 : Tidak ada autokorelasi spasial antar
Lokasi
H1 : Ada autokorelasi spasial antar lokasi
Berdasarkan hal tersebut maka pengambilan keputusan pada uji ini adalah tolak Ho jika ∣Zhit | > Za atau
2
probability < 0,05 dengan taraf signifikansi sebesar a = 5%
Tabel 4. Uji Moran's I
|
Test |
Mi Df |
Nilai Uji |
Probability |
|
Moran’s I (error) |
0,2007 |
6,6695 |
0,00000 |
|
Lagrange Multiplier (lag) |
1 |
68,9162 |
0,00000 |
|
Robust LM (lag) |
1 |
34,6977 |
0,00000 |
|
Lagrange Multiplier (error) |
1 |
38,8264 |
0,00000 |
|
Robust LM (error) |
1 |
4,6079 |
0,03183 |
|
Lagrange Multiplier (SARMA) |
1 |
73,5241 |
0,00000 |
Sumber: Data diolah (2022)
Berdasarkan hasil output di atas, terlihat bahwa nilai probability pada Moran’s I sebesar 0,00000. Oleh karena itu, dapat disimpulkan bahwa H0 ditolak sehingga dapat dikatakan dalam data terdapat autokorelasi spasial antar wilayah yang ditandai dengan diperolehnya nilai probability sebesar 0,00000< a.
-
2) Lagrange Multiplier (lag).
Hipotesis:
H0 : ρ = 0 (Tidak ada ketergantungan lag
spasial)
H1 :p ≠ 0 (Ada ketergantungan lag
spasial)
dengan taraf signifikansi, yaitu:
a = 5%
Berdasarkan uraian di atas sehingga pengambilan keputusan pada uji ini adalah tolak Ho bila LMp > X^q) atau probability < 0,05.
Hasil output dengan menggunakan software Open Geoda sebagai berikut:
Tabel 5. Uji Lagrange Multiplier
|
Test |
Mi Df |
Nilai Uji |
Probability |
|
Moran’s I (error) |
0,2007 |
6,6695 |
0,00000 |
|
Lagrange Multiplier (lag) |
1 |
68,9162 |
0,00000 |
|
Robust LM (lag) |
1 |
34,6977 |
0,00000 |
|
Lagrange Multiplier (error) |
1 |
38,8264 |
0,00000 |
|
Robust LM (error) |
1 |
4,6079 |
0,03183 |
|
Lagrange Multiplier (SARMA) |
1 |
73,5241 |
0,00000 |
Sumber: Data diolah (2022)
Berdasarkan hasil output di atas, terlihat bahwa nilai probability pada Lagrange Multiplier (lag) sebesar 0,00000. Oleh karena itu, dapat disimpulkan bahwa H0 ditolak sehingga dapat dikatakan dalam data terdapat ketergantungan spasial pada variabel respon yang ditandai dengan diperolehnya nilai probability sebesar 0.00000 < 0.05 yang artinya analisis dapat dilanjutkan dengan menggunakan model SAR.
-
b. Uji G (Simultan)
Hipotesis:
H0 : Variabel dependen tidak dipengaruhi
secara signifikan oleh salah satu faktor independen yang diambil bersama-sama.
H1 : Variabel dependen dipengaruhi secara
signifikan oleh paling sedikit satu variabel independen.
Berdasarkan hal tersebut maka pengambilan keputusan pada uji ini adalah tolak Ho jika | >Zhit | > Za atau p — value < 2
0,05.
Hasil output dengan menggunakan software SPSS sebagai berikut:
Tabel 6. Uji G (Simultan)
|
Model |
-2 Log Likelihood |
ChiSquare |
df |
Sig. |
|
Intercept Only |
1323,802 | |||
|
Final |
0,000 |
1323,513 |
513 |
0,000 |
Sumber: Data diolah (2022)
Berdasarkan output di atas, Ho ditolak karena nilai signifikansi uji G yaitu 0,000 lebih kecil dari ambang batas signifikansi 0,05. Akibatnya, dapat dikatakan bahwa setidaknya satu variabel independen secara signifikan mempengaruhi variabel dependen.
-
c. Uji Kecocokan Model Keseluruhan Hipotesis:
Ho : θi = 0,∀i (Model SAR tidak sesuai)
Hi : ∃ιθι ≠ 0 (Model SAR sesuai)
dengan taraf signifikansi, yaitu:
a = 5%
Berdasarkan hal tersebut, jika H0 ditolak dalam pengujian ini, berarti probability <0,05.
Hasil output dengan menggunakan software Open Geoda sebagai berikut:
Tabel 7. Uji Kecocokan Model Keseluruhan
|
Test |
Df |
Value |
Probability |
|
Likelihood Ratio Test |
1 |
72,2264 |
0,00000 |
Sumber: Data diolah (2022)
Berdasarkan output yang dihasilkan nilai probability Likelihood Ratio Test 0,00000. Model SAR yang dihasilkan adalah model yang cocok, karena ditentukan dengan tingkat signifikansi =5%.
-
d. Uji Signifikansi Parsial
Hipotesis:
Ho: βι = 0 (Parameter tidak signifikan), i. = 1,2,310
Hi: βι ≠ 0 (Parameter signifikan)
Penolakan H0 dilakukan apabila nilai W >
Y 2
A-(O1V)
Hasil output dengan menggunakan software Open Geoda sebagai berikut:
Tabel 8. Uji Sgnifikansi Parsial
|
Test |
Df |
Value |
Probability |
|
Likelihood Ratio Test |
1 |
72,2264 |
0,00000 |
Sumber: Data diolah (2022)
-
e. Uji Multikolinearitas
Uji multikolinearitas memiliki asumsi sebagai berikut.
-
1. Multikolinearitas berkembang jika VIF >
-
10 dan nilai Tolerance 0,10
-
2. Multikolinearitas tidak terjadi jika VIF 10
dan nilai Tolerance > 0.10
Hasil ujinmultikolinearitas disesuaikan dengan Tabel berikut ini.
Tabel 9. Uji Multikolinearitas
|
B |
t |
Sig. |
VIF |
|
(constant) |
0,894 | ||
|
A1 |
0,030 |
0,972 |
1,056 |
|
A2 |
0,105 |
2,896 |
1,473 |
|
A3 |
0,078 |
-2,388 |
1,185 |
|
A4 |
0,300 |
-7,405 |
1,838 |
|
A5 |
0,131 |
-3,574 |
1,492 |
|
A6 |
0,128 |
-3,194 |
1,793 |
|
A7 |
0,073 |
2,359 |
1,057 |
|
A8 |
0,082 |
2,432 |
1,268 |
|
A9 |
0,237 |
5,291 |
2,254 |
|
A10 |
0,227 |
6,727 |
1,274 |
Sumber: Data diolah (2022)
-
f. Pemeriksaan Kesesuaian Model
Nilai AIC digunakan untuk menentukan apakah model regresi logistik ordinal spasial sudah sesuai. Nilai AIC model regresi logistik ordinal spasial adalah 1360,72, dan nilai R-squares-nya adalah 0,609193, yang berarti bahwa 60,92% variansi variabel respon Y (IKP) dapat dijelaskan oleh variabel independen model, dengan sisanya varians dijelaskan oleh variabel di luar model, seperti yang ditunjukkan pada tabel di bawah ini.
Tabel 10. Pemeriksaan Kesesuaian Model
|
Data set: |
Batas Kabupaten Kota Desember 2019 Dukcapil | ||
|
Spatial Weight: |
Matriks Pembobot Spasial | ||
|
Dependent Variable: |
y |
Number of Observations: |
514 |
|
Mean dependent var: |
5,05447 |
Number of Variables: |
12 |
|
S.D. dependent var: |
1,40903 |
Degrees of Freedom: |
502 |
|
Lag coeff (Rho): |
0,259657 | ||
|
R-squared: |
0,609193 |
Log Likelihood: |
- 668,361 |
|
Sq. Correlation: |
- |
Akaike info criterion: |
1360,72 |
Sumber: Data diolah (2022)
-
g. Spatial Autoregressive Model (SAR)
Berdasarkan data diatas penentuan model menggunakan regresi SAR dengan pembobotan queen contiguity. Penentuan model SAR menggunakan software Open Geoda, model yang diperoleh sebagai berikut:
Tabel 11. Penentuan Model SAR
|
Variable |
Coefficient |
z-value |
Probability |
|
W_y |
0,259657 |
8,83538 |
0,00000 |
|
Constant |
0,799839 |
0,962537 |
0,33578 |
|
Ai |
1,21614e-06 |
0,112776 |
0,91021 |
|
A2 |
-8,97791e-06 |
-0,466503 |
0,64086 |
|
A3 |
-0,0351118 |
-2,400313 |
0,01626 |
|
A4 |
-0,0405617 |
-6,77859 |
0,00000 |
|
A5 |
-0,00797372 |
-2,5495 |
0,01079 |
|
A6 |
-0,00689079 |
-2,99453 |
0,00275 |
|
A7 |
0,00927928 |
2,22673 |
0,02597 |
|
A8 |
0,00677942 |
1,19319 |
0,2327 |
|
A9 |
0,0435406 |
4,96378 |
0,00000 |
|
A10 |
0,0168314 |
4,28783 |
0,00002 |
Sumber: Data diolah (2022)
Dari hasil output di atas, maka diperoleh nilai odds ratio untuk setiap variabel dituliskan dalam tabel dibawah ini.
Tabel 12. Nilai Odds Ratio Variabel Penelitian
|
Variabel Penelitian |
Odds Ratio |
|
Wy |
1.296485316 |
|
Constant |
2.225182645 |
|
X1 |
1.000001216 |
|
X2 |
1.000008978 |
|
X3 |
0.9654974676 |
|
X4 |
0.9602499153 |
|
X5 |
0.9920579858 |
|
X6 |
0.9334126434 |
|
X7 |
1.009322466 |
|
X8 |
1.006802452 |
|
X9 |
1.0445024 |
|
X10 |
1.016973846 |
Sumber: Data diolah (2022)
Sehingga persamaan regresi logistik ordinal spasial yang terbentuk, yaitu:
p(y ≤s∣x) 1-P(Y ≤ six')
■)
Log (
= as — Xβ — pWy + ε
Loa ( p(Y ≤ s∣x) — O 799839 +
Log (i-p(Y ≤ s∣x)) = 0 99839 +
1.21614e — 06X1 — 8.977991e — 06X2 — 0.0351118X3 — 0.0405617X4 — 0.00797372X5 — 0.00689079X6 + 0.00927928X7 + 0.00677942X8 + 0.0435406X9 + 0.0168314X10 + 0.259657Wy
Berdasarkan tabel diatas, maka interpretasi model regresinlogistik ordinalnspasial yang diperoleh dapat dijelaskan sebagai berikut:
-
1. Variabel laju pertumbuhan penduduk memiliki odds ratio sebesar 0,9654974676. Jika variabel bebas lainnya diasumsikan konstan, hal ini dapat dibaca karena setiap laju pertumbuhan penduduk meningkat sebesar satu persen menyebabkan rasio tingkat ketahanan pangan kelompok 1 terhadap kelompok lainnya turun sebesar 0,9654974676 kali.
-
2. Proporsi penduduk miskin memiliki koefisien regresi sebesar -0,0405617 dan odds ratio sebesar 0,9602499153. Rasio tingkat ketahanan pangan kelompok 1 (kerentanan pangan tinggi) terhadap kelompok lain berkurang sebesar 0,9602499153 kali jika proporsi penduduk miskin dinaikkan sebesar 1%, dengan syarat semua variabel bebas lainnya dianggap konstan.
-
3. Dengan odd rasio 0,9920579858, koefisien regresi untuk sebagian rumah tanpa akses
listrik adalah -0,00797372. Hal ini menunjukkan bahwa, jika variabel independen lainnya dipertahankan konstan, maka rasio ketahanan pangan kelompok 1 (kerawanan pangan tinggi) terhadap kelompok lainnya berkurang sebesar 0,9920579858 kali jika fraksi keluarga yang tidak memiliki akses listrik naik sebesar satu persen.
-
4. Dengan odd rasio 0,933412643, maka koefisien regresi untuk sebagian kecil keluarga yang tidak memiliki akses air bersih adalah -0,00689079. Hal ini menunjukkan bahwa jika variabel bebas lainnya dipertahankan konstan, rasio tingkat ketahanan pangan dari kelompok 1 (kerawanan pangan tinggi) terhadap kelompok lainnya berkurang sebesar 0,933412643 kali untuk setiap kenaikan persen jumlah keluarga yang tidak memiliki akses air bersih.
-
5. Proporsi balita yang menderita gizi buruk dan stunting memiliki nilai koefisien regresi sebesar 0,00917928 dan odds ratio sebesar 1,009322466. Perbandingan tingkat ketahanan pangan dari kelompok 1 (kerentanan pangan tinggi) dengan
kelompok lainnya akan meningkat sebesar 1,009322466 kali lipat jika persentase balita gizi buruk dan stunting naik satu persen, dengan asumsi variabel independen lainnya dipegang konstan.
-
6. Odds ratio untuk variabel indeks pembangunan manusia sebesar 1,0445024, dan koefisien regresi sebesar 0,0435406. Hal ini menunjukkan bahwa jika variabel bebas lainnya dipertahankan konstan, maka perbandingan derajat ketahanan pangan dari kelompok 1 (kerentanan pangan tinggi) dengan kelompok lain akan meningkat sebesar 1,0445024 kali untuk setiap kenaikan satu satuan indeks pembangunan manusia.
-
7. Koefisien regresi variabel elemen geografis adalah 0,0168314, dan rasio odds-nya
adalah 1,016973846. Hal ini menunjukkan bahwa jika variabel bebas lainnya
dipertahankan konstan, peningkatan unsur geografis satu satuan menyebabkan rasio derajat ketahanan pangan dari kelompok 1 (kerentanan pangan tinggi) terhadap kelompok lainnya tumbuh sebesar 1,016973846 kali.
-
8. Koefisien regresi Wy adalah 0,259657, dan rasio odds-nya adalah 1,296485316.
Perbandingan derajat ketahanan pangan dari kelompok 1 (kerentanan pangan tinggi) dengan kelompok lain akan meningkat sebesar 1,296485316 kali jika cakupan antar wilayah bertambah satu satuan, dengan syarat variabel bebas lainnya dianggap konstan
Berdasarkan temuan contoh kasus dengan menggunakan spatial autoregressive model (SAR), dapat dikatakan bahwa model SAR merupakan model regresi terbaik untuk memprediksi keadaan ketahanan pangan di Indonesia berdasarkan kabupaten dan kota pada tahun 2020. Nilai AIC dari model yang dihasilkan dipertimbangkan saat memilih model yang optimal. Nilai AIC untuk model SAR adalah 1360,2. Laju pertumbuhan penduduk, persentase penduduk miskin, persentase rumah tangga tanpa akses listrik, persentase rumah tangga tanpa akses air bersih, persentase balita dan stunting, indeks pembangunan manusia, dan elemen spasial merupakan faktor-faktor yang menyebabkan signifikan terhadap variabel respon.
DAFTAR PUSTAKA
Badan Ketahanan Pangan. (2020). Panduan Penyusunan Peta Ketahanan dan Kerentanan Pangan Tingkat Provinsi.
Badan Ketahanan Pangan Kementrian Pertanian. (2019). Indeks Ketahanan Pangan 2020.
Ghozali, Imam. (2018). Aplikasi Analisis Multivariate dengan Program IBM SPSS 25. Badan Penerbit Universitas
Diponegoro: Semarang.
Hosmer, D. W., & Lemeshow, S. (2000).
Applied Logistic Regression (2nd ed.). John Wiley & Sons, Inc.
Lee, J. and Wong, D. W. S. (2001) Statiscal Analysis with ArcView Gis. Canada: John Wiley & Sons Inc.
Trivanni, Ikrimah Afifah (2018).
Perbandingan Model Regresi Logistik Ordinal Spasial Dan Non Spasial Pada Status Ketahanan Pangan
Kabupaten/Kota di Indonesia Tahun
2016. 2016.
https://dspace.uii.ac.id/handle/123456789 /8034
Webb, P., dan Rogers, B. 2003. Addressing the 'In' in Food Insecurity. Washington D.C.: United States Agency for
Internastional Development Office of Food for Peace.
288
Discussion and feedback