PERBANDINGAN REGRESI ROBUST PENDUGA MM DENGAN METODE RANDOM SAMPLE CONSENSUS DALAM MENANGANI PENCILAN

E-Jurnal Matematika Vol. 3, No.2 Mei 2014, 45-52

ISSN: 2303-1751

PERBANDINGAN REGRESI ROBUST PENDUGA MM DENGAN METODE RANDOM SAMPLE CONSENSUS DALAM MENANGANI PENCILAN

Ni Putu Nia Irfagutami¹, I Gusti Ayu Made Srinadi², I Wayan Sumarjaya³

• ^1,2,3Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: ¹1, ²srinadiigustiayumade@yahoo.co.id, ³sumarjaya@unud.ac.id,

Abstract

The presence of outliers in observation can result in biased in parameter estimation using ordinary least square (OLS). Robust regression MM-estimator is one of the estimations methods that able to obtain a robust estimator against outliers. Random sample consensus (ransac) is another method that can be used to construct a model for observations data and also estimating a robust estimator against outliers. Based on the study, ransac obtained model with less biased estimator than robust regression MM-estimator.

Keywords: Outlier, Robust Regression, MM-estimate, ransac

• 1.    Pendahuluan

Model regresi dapat menggambarkan hubungan antarpeubah kuantitatif, sehingga satu atau lebih peubah dapat digambarkan oleh peubah lainnya. Model regresi linear sederhana, yakni Y_i = β₀ + β₁X_i+ε₁ merupakan suatu model yang terdiri dari satu peubah bebas dan satu peubah respons. Parameter-parameter yang membentuk model selanjutnya diduga dengan menggunakan metode kuadrat terkecil (MKT).

Metode kuadrat terkecil merupakan metode pendugaan parameter yang dilakukan dengan meminimumkan jumlah simpangan kuadratζ> = Σ^₁(y,-β_a-β₁X_i)². Asumsi kenormalan, kehomogenan ragam, dan tidak terjadi autokorelasi pada komponen sisaan atau galat merupakan syarat dalam penggunaan metode ini. Apabila asumsi ini terpenuhi maka penduga yang dihasilkan akan bersifat takbias. Namun, tidak jarang ditemukan kasus dengan asumsi kenormalan, kehomogenan ragam, dan tidak terjadi autokorelasi tidak terpenuhi. Salah satu penyebabnya adalah adanya pencilan

dalam data amatan yang memengaruhi proses analisis. Salah satu alternatif yang dapat digunakan untuk mengatasi permasalah ini yakni dengan menerapkan metode regresi robust.

Regresi robust merupakan suatu metode yang dapat menghasilkan penduga parameter yang kekar terhadap pencilan. Metode ini tetap menggunakan keseluruhan data, termasuk data pencilan, namun dengan memberikan bobot yang kecil pada data pencilan. Metode lain yang dapat diterapkan yakni ransac diperkenalkan pertama kali oleh Fischler dan Bolles pada tahun 1981 sebagai suatu paradigma dalam pembentukan model untuk data eksperimen. Metode ini menggunakan sedikit mungkin himpunan data dan memperluas himpunan ini dengan sekumpulan data yang konsisten (Fischler dan Bolles, 1981). Perbandingan kedua metode yang samasama mampu menghasilkan penduga yang kekar terhadap pencilan merupakan fokus dalam penelitian ini. Ketidakbiasan penduga

yang dihasilkan oleh masing-masing metode akan menjadi acuan dalam penelitian ini.

• 2.    Metode Penelitian

Data yang digunakan pada penelitian ini merupakan data simulasi dengan satu peubah bebas (X) dan satu peubah respons (Y). Data dibangkitkan dengan bantuan program R versi 2.15.3 Adapun tahapan yang dilakukan dalam penelitian ini, yakni (1) Pembangkitan data. Adapun pembangkitan data dilakukan dengan ketentuan, peubah bebas (X) terdiri dari 100 amatan dengan nilai-nilai peubah X adalah 1, 2, …,  100. Nilai sisaan yang dibangkitkan

merupakan data yang berdistribusi normal dengan rataan nol dan ragam satu sebanyak 100. Pembangkitan data pencilan, yang mana pada penelitian pencilan minor merupakan data yang berdistribusi normal dengan rataan lima dan standar deviasi 0,1, sedangkan pencilan mayor merupakan data yang berdistribusi normal dengan rataan delapan dan standar deviasi 0,1. Adapun pencilan yang dibangkitkan yakni sebesar 5%, 10%, 15%,

20%, 25%, dan 30% dari data, baik pencilan minor maupun mayor. Penempatan pencilan pada bagian bawah, tengah dan bagian atas dari gugus data dilakukan untuk melihat pengaruh posisi pencilan terhadap proses analisis. Setelah terdapat data sisaan yang mengandung pencilan dan peubah bebas, maka dapat dibangkitkan data untuk peubah respon (Y). Ditentukan terlebih dahulu hubungan peubah bebas dan peubah respons yaitu γ = p_o+ p_lx+_ε}. Pada penelitian ini ditetapkan nilai P$ — ^ dan Pl = 3. Berdasarkan nilai peubah bebas, koefisien regresi, dan nilai sisaan yang mengandung pencilan, maka akan didapat 36 kelompok data peubah respons yang mengandung pencilan. (2) Melakukan uji Anderson-Darling untuk melihat kenormalan data. (3) Melakukan analisis data dengan regresi robust penduga MM dan (4) random sample consensus untuk setiap data yang dimiliki. (5) Membandingkan penduga parameter yang dihasilkan oleh metode regresi

robust penduga MM dan ransac untuk melihat metode manakah yang menghasilkan penduga parameter yang lebih baik.

• 3.    Hasil dan Pembahasan

Setelah dibangkitkan data peubah bebas, data sisaan, dan data peubah respon baik dengan pencilan maupun tanpa pencilan, maka dilakukan pendugaan parameter dengan menggunakan metode kuadrat terkecil. Terdapat dua asumsi yang harus dipenuhi dalam menggunakan metode ini, yakni data yang digunakan menyebar normal dan memiliki ragam yang homogen. Apabila kedua asumsi ini terpenuhi maka penduga yang dihasilkan akan bersifat takbias.

Metode kuadrat terkecil merupakan suatu metode pendugaan parameter dengan meminimumkan jumlah kuadrat galat. Jumlah kuadrat galat dapat dituliskan sebagai berikut: ■n

^^^_i² t=l

■n

= ∑(γ_i-p₀-p₁x_iY, (1)

Untuk meminimumkan jumlah kuadrat galat maka persamaan (1) akan diturunkan secara kalkulus terhadap parameter β C dan Pl . Kedua

persamaan turunan tersebut selanjutnya disamakan dengan nol. Dengan demikian diperoleh nilai-nilai penduga parameter sebagai berikut,

I ₌ ∑^₁⅛ - X)(y_i - y)

• ¹    ∑Γ=₁⅛-^² '

Setelah dilakukan analisis pada masing-masing kelompok data yang mengandung pencilan dengan menggunakan metode kuadrat terkecil, maka dihitung nilai sisaan untuk masing-masing model. Nilai sisaan ini selanjutnya digunakan untuk melakukan pengujian asumsi kenormalan dengan menggunakan uji Anderson-Darling.

Uji Anderson-Darling melibatkan fungsi distribusi kumulatif dari sebaran data. Misalkan data yang akan diuji diasumsikan berdistribusi normal dengan tingkat signifikan α, maka statistik uji yang digunakan adalah A² =-n-S, dengan n

^s=S^2f ^^1] M^f^)^+ln(¹ ^ ^f‰ι-Λl

i=l

dengan

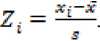
Adapun hipotesis yang diuji yakni: H0 : data mengikuti sebaran normal H1 : data tidak mengikuti sebaran normal, dengan kaidah keputusannya yakni jika λ² lebih besar dari nilai kritis uji Anderson-Darling maka tolak H0 dan jika A lebih kecil dari nilai kritis uji Anderson-Darling maka H0 gagal ditolak. Apabila nilai p-value lebih kecil dari α maka tolak H0, apabila sebaliknya, terima H0.

Berdasarkan hasil uji Anderson-Darling pada data sisaan untuk masing-masing model yang diduga dengan metode kuadrat terkecil, didapat bahwa semua data yang diberikan pencilan, baik pencilan minor maupun mayor dengan persentase 5%, 10%, 15%, 20%, 25%, dan 30% pada bagian bawah, tengah, dan atas, memiliki p-value yang lebih kecil dari nilai alfa yang ditentukan, yakni a = 0,05. Hal ini berarti bahwa semua data yang mengandung pencilan tidak memenuhi asumsi kenormalan atau dapat dikatakan data tidak menyebar normal. Sehingga akan diterapkan metode regresi robust penduga MM dan metode ransac dalam analisis.

Regresi robust merupakan salah satu metode regresi yang mampu menghasilkan penduga parameter yang robust (kekar) terhadap pencilan. Metode ini bekerja dengan memberikan bobot pada pencilan yang kemudian membatasi pengaruh pencilan tersebut. Penduga MM merupakan salah satu metode estimasi yang diperkenalkan pertama kali oleh Yohai (1987) sebagai metode yang menggabungkan metode penduga M (Maximum

Likelihood) dan penduga S (Scale). Regresi robust dengan penduga S akan menjamin penduga parameter memiliki nilai breakdown point yang tinggi dan regresi robust dengan penduga M akan menjamin penduga parameter memiliki efisiensi yang tinggi. Hal inilah yang menyebabkan metode regresi robust penduga MM memiliki tingkat efisiensi dan breakdown point yang tinggi.

Pendugaan parameter dengan metode penduga MM dilakukan dengan dua tahap. Pertama, pendugaan parameter regresi awal yang diawali dengan menghitung nilai penduga skala menggunakan metode penduga S. Kedua, menaksir penduga parameter regresi akhir dengan menggunakan metode penduga M. Adapun langkah-langkah pendugaan parameter dengan menggunakan metode penduga MM, yakni, (1) Menghitung nilai awal penduga parameter b dengan menggunakan penduga S

(high breakdown point), yang mana penduga awal yang dihasilkan tidak harus efisien. Kemudian gunakan penduga ini untuk menghitung residual,

ε_i,₀= y-χ^τ b. (2) Dari nilai residual pada langkah pertama, dihitung penduga skala, ^sn = s(ε₁(β),ε₂(β),-,ε_n(β)) yang

didefinisikan sebagai solusi dari

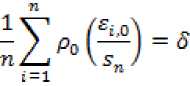
dengan S merupakan konstanta yang memenuhi s = E(Φ,p(∞y),φ berdistribusi normal standar dan P (u) merupakan fungsi objektif

yang menurut (Rousseeuw dan Leroy, 1987) harus memenuhi, (i) p merupakan fungsi simetris dan terdiferensialkan secara kontinu, dan p(0) = 0, (ii) jika terdapat α > 0 , maka p akan meningkat pada ^o_f ^] dan konstan pada Da, co) , (iii)           . Fungsi objektif yang

Pkaj 2

digunakan pada langkah ini adalah fungsi objektif Tukey Bisquare,

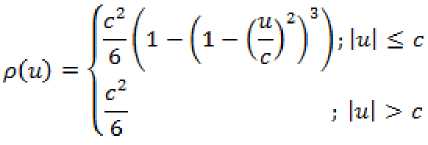
dengan c = 1,56 [3].

(3) Setelah mendapatkan nilai sisaan ⅞.0 dan penduga skala S„ , hitung pembobot awal <X□) sesuai dengan fungsi pembobot Tukey Bisquare,

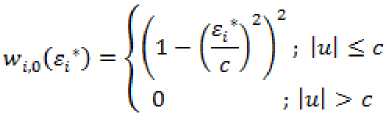
dengan ^sI_jO^{il -} ? dan c = 4,68 (Yohai,

• 1987) . Kemudian dihitung nilai penduga MM sebagai:

b_l = (x^rψ,.₁xr¹x⅜,.₁κ dengan W∖-ι merupakan matriks diagonal yang elemen diagonalnya adalah nilai dari fungsi pembobot ^wi,l-l> dengan l menyatakan iterasi. (4) Hitung nilai ∑7=ιl⅛ I , dengan ¾ι = y-×^r b _l. (5) Ulangi langkah kedua hingga empat. Iterasi dihentikan ketika telah mendapatkan nilai ∑7=ιl ⅛ I yang konvergen.

Setelah didapat penduga parameter dengan menggunakan metode regresi robust penduga MM, maka dicari selang kepercayaan masing-masing     penduganya.      Selang

kepercayaan digunakan untuk melihat sifat

ketakbiasan penduga yang dihasilkan. Apabila selang kepercayaan mencakup nilai parameter yang sebenarnya, maka penduga parameter yang dihasilkan memiliki sifat takbias. Berdasarkan selang kepercayaan 95% diperoleh bahwa metode regresi robust menghasilkan penduga intercept (^o) yang berbias saat terdapat pencilan minor sebesar 10%, 15%, 20%, 25%, dan 30% pada bagian bawah gugus data, pencilan minor sebesar 30% pada bagian tengah gugus data, pencilan minor sebesar 20%, 25%, dan 30% pada bagian atas gugus data, dan saat terdapat pencilan mayor sebesar 30% pada bagian bawah gugus data.

Metode ini juga menghasilkan penduga slope (βl) yang berbias saat terdapat pencilan minor sebesar 10%, 15%, 20%, 25%, dan 30% pada bagian bawah gugus data, pencilan minor sebesar 15%, 20%, 25%, dan 30% pada bagian atas gugus data, dan saat terdapat pencilan mayor sebesar 30% pada bagian bawah gugus data. Untuk jenis data pencilan lainnya, metode regresi robust penduga MM menghasilkan penduga yang takbias. Hal ini lebih jelasnya dapat dilihat pada Tabel 1.

Tabel 1 Selang Kepercayaan 95% βf∖ dan Pl dengan Metode Regresi Robust Penduga MM

Pencilan		% Pencil-an	β0		Keterangan	β1		Keterangan
			Batas Bawah	Batas Atas		Batas Bawah	Batas Atas
Minor	Bawah	5%	1.6173	2.4861	Tidak Bias	2.9915	3.0066	Tidak Bias
		10%	2.1556	3.2633	Bias	2.9800	2.9991	Bias
		15%	3.7913	5.3483	Bias	2.9500	2.9766	Bias
		20%	4.8335	6.4103	Bias	2.9358	2.9628	Bias
		25%	5.5666	6.9994	Bias	2.9289	2.9535	Bias
		30%	6.1440	7.5736	Bias	2.9225	2.9471	Bias
	Tengah	5%	1.7224	2.5447	Tidak Bias	2.9912	3.0054	Tidak Bias
		10%	0.5606	3.7267	Tidak Bias	2.9846	3.0116	Tidak Bias
		15%	1.6920	2.7926	Tidak Bias	2.9885	3.0076	Tidak Bias
		20%	1.7275	3.2540	Tidak Bias	2.9854	3.0116	Tidak Bias
		25%	1.8773	3.9812	Tidak Bias	2.9795	3.0156	Tidak Bias
		30%	2.1315	4.5669	Bias	2.9974	3.0191	Tidak Bias
	Atas	5%	1.7138	2.5477	Tidak Bias	2.9904	3.0047	Tidak Bias
		10%	1.6207	2.5320	Tidak Bias	2.9917	3.0071	Tidak Bias
		15%	0.5354	2.0460	Tidak Bias	3.0127	3.0385	Bias
		20%	-0.1317	1.5643	Bias	3.0329	3.0619	Bias
		25%	-0.2122	1.3202	Bias	3.0428	3.0690	Bias
		30%	-0.2361	1.1859	Bias	3.0502	3.0748	Bias
Mayor	Bawah	5%	1.6137	2.4642	Tidak Bias	2.9919	3.0066	Tidak Bias
		10%	1.6490	2.5417	Tidak Bias	2.9907	3.0062	Tidak Bias
		15%	1.6721	2.5997	Tidak Bias	2.9900	3.0059	Tidak Bias
		20%	1.6524	2.5843	Tidak Bias	2.9903	3.0061	Tidak Bias
		25%	1.7562	2.7917	Tidak Bias	2.9871	3.0050	Tidak Bias
		30%	8.7650	11.0408	Bias	2.8752	2.9145	Bias
	Tengah	5%	1.7244	2.5402	Tidak Bias	2.9914	3.0052	Tidak Bias
		10%	1.7175	2.5462	Tidak Bias	2.9910	3.0052	Tidak Bias
		15%	1.6936	2.5612	Tidak Bias	2.9905	3.0056	Tidak Bias
		20%	1.6856	2.5917	Tidak Bias	2.9905	3.0060	Tidak Bias
		25%	1.6766	2.6268	Tidak Bias	2.9897	3.0060	Tidak Bias
		30%	1.6463	2.8850	Tidak Bias	2.9873	3.0087	Tidak Bias
	Atas	5%	1.7153	2.5468	Tidak Bias	2.9904	3.0047	Tidak Bias
		10%	1.6885	2.5351	Tidak Bias	2.9909	3.0056	Tidak Bias
		15%	1.6943	2.5675	Tidak Bias	2.9902	3.0052	Tidak Bias
		20%	1.7552	2.6586	Tidak Bias	2.9873	3.0028	Tidak Bias
		25%	1.7428	2.6517	Tidak Bias	2.9879	3.0034	Tidak Bias
		30%	1.7197	2.6484	Tidak Bias	2.9984	3.0042	Tidak Bias

Kemudian metode lain yang dapat digunakan untuk mendapat penduga yang kekar terhadap pencilan yakni metode ransac. Ransac diperkenalkan pertama kali oleh Fischler dan Bolles (1981) sebagai suatu metode pembentukan model bagi data eksperimen. Proses pembentukan model terbaik dengan menggunakan metode ini sangatlah berbeda dengan metode regresi robust. Apabila regresi robust menggunakan seluruh data dalam pendugaan parameter, maka random sample consensus menggunakan seminimum mungkin data untuk membentuk model yang mampu menjelaskan keseluruhan data ( Fischler dan Bolles, 1981).

Adapun proses pembentukan model dengan menggunakan metode ransac (3), yakni (1) dipilih 2 data secara acak dari sekumpulan 100 data. Selanjutnya kumpulan 2 data ini disebut sebagai himpunan “^1 . (2) Bentuk model dengan menggunakan 2 data tersebut, sebut M₁ . Pembentukan model dapat dilakukan dengan metode kuadrat terkecil (least square). (3) Berdasarkan model M₁ , bentuk himpunan baru (¾*) dari keseluruhan data yang mana anggota himpunannya merupakan data yang memiliki sisaan dalam toleransi error (t). Himpunan ini selanjutnya disebut sebagai consensus set ^l . (4) Jika (-1 ^) lebih besar dari batasan (threshold), T, maka gunakan ¾ untuk membentuk model baru, yakni M₁-. (5) Jika (V) lebih kecil dari batasan (threshold), T, maka pilih secara acak himpunan baru S 2 dan ulangi langkah (2).

Setelah didapatkan penduga parameter dengan menggunakan metode ransac, maka dicari selang kepercayaan masing-masing penduganya. Berdasarkan selang kepercayaan 95% diketahui bahwa metode ransac menghasilkan penduga parameter β^ yang berbias saat terdapat pencilan minor pada bagian bawah gugus data sebesar 25% dan

30%, dan pada bagian tengah gugus data sebesar 25% dan 30%. Ransac juga menghasilkan penduga parameter /?1 yang berbias saat terdapat pencilan minor pada bagian bawah gugus data sebesar 25% dan 30% dan juga saat terdapat pencilan minor sebesar 25% dan 30% pada bagian atas gugus data. Untuk jenis data lainnya, ransac menghasilkan penduga parameter yang bersifat takbias. Hal ini lebih jelasnya dapat dilihat pada Tabel 2.

Tabel 2 Selang Kepercayaan 95% ^G dan Λl dengan Metode Ransac

Pencilan		% Pencil-an	β0		Keterangan	β1		Keterangan
			Batas Bawah	Batas Atas		Batas Bawah	Batas Atas
Minor	Bawah	5%	1.5705	2.4361	Tidak Bias	2.9926	3.0070	Tidak Bias
		10%	1.5318	2.5237	Tidak Bias	2.9914	3.0075	Tidak Bias
		15%	1.4675	2.6009	Tidak Bias	2.9904	3.0083	Tidak Bias
		20%	1.5143	2.7695	Tidak Bias	2.9882	3.0076	Tidak Bias
		25%	6.3417	7.3958	Bias	2.9271	2.9446	Bias
		30%	7.1327	8.0673	Bias	2.9200	2.9359	Bias
	Tengah	5%	1.7240	2.4811	Tidak Bias	2.9923	3.0052	Tidak Bias
		10%	1.7135	2.4708	Tidak Bias	2.9922	3.0050	Tidak Bias
		15%	1.6880	2.4685	Tidak Bias	2.9922	3.0056	Tidak Bias
		20%	1.6812	2.4827	Tidak Bias	2.9923	3.0056	Tidak Bias
		25%	1.7051	2.5243	Tidak Bias	2.9908	3.0044	Tidak Bias
		30%	1.8892	2.7211	Tidak Bias	2.9893	3.0030	Tidak Bias
	Atas	5%	1.7112	2.4953	Tidak Bias	2.9909	3.0050	Tidak Bias
		10%	1.6711	2.4758	Tidak Bias	2.9912	3.0065	Tidak Bias
		15%	1.7948	2.6465	Tidak Bias	2.9878	3.0050	Tidak Bias
		20%	1.7147	2.5840	Tidak Bias	2.9869	3.0054	Tidak Bias
		25%	0.3074	1.2391	Bias	3.0539	3.0700	Bias
		30%	0.1732	1.0939	Bias	3.0596	3.0752	Bias
Mayor	Bawah	5%	1.5705	2.4361	Tidak Bias	2.9926	3.0070	Tidak Bias
		10%	1.5318	2.5237	Tidak Bias	2.9914	3.0075	Tidak Bias
		15%	1.4667	2.6009	Tidak Bias	2.9904	3.0083	Tidak Bias
		20%	1.5143	2.7695	Tidak Bias	2.9882	3.0076	Tidak Bias
		25%	1.5215	2.9693	Tidak Bias	2.9856	3.0074	Tidak Bias
		30%	1.0735	2.7088	Tidak Bias	2.9892	3.0131	Tidak Bias
	Tengah	5%	1.7240	2.4811	Tidak Bias	2.9923	3.0052	Tidak Bias
		10%	1.7135	2.4708	Tidak Bias	2.9922	3.0050	Tidak Bias
		15%	1.6880	2.4685	Tidak Bias	2.9922	3.0052	Tidak Bias
		20%	1.6812	2.4827	Tidak Bias	2.9923	3.0056	Tidak Bias
		25%	1.7051	2.5243	Tidak Bias	2.9908	3.0044	Tidak Bias
		30%	1.7544	2.5698	Tidak Bias	2.9911	3.0045	Tidak Bias
	Atas	5%	1.7112	2.4953	Tidak Bias	2.9909	3.0050	Tidak Bias
		10%	1.6711	2.4758	Tidak Bias	2.9912	3.0065	Tidak Bias
		15%	1.6672	2.5029	Tidak Bias	2.9900	3.0068	Tidak Bias
		20%	1.8465	2.7319	Tidak Bias	2.9845	3.0034	Tidak Bias
		25%	1.6924	2.5707	Tidak Bias	2.9869	3.0069	Tidak Bias
		30%	1.6605	2.5605	Tidak Bias	2.9867	3.0086	Tidak Bias

4. Kesimpulan

Adanya pencilan pada bagian ujung gugus data memengaruhi proses pendugaan parameter. Hal ini dilihat dari penduga yang dihasilkan oleh metode regresi robust penduga MM bersifat bias saat terdapat pencilan minor sebesar 10% hingga 30% pada bagian bawah gugus data, pencilan minor sebesar 15% hingga 30% pada bagian atas gugus data, dan pada saat terdapat pencilan mayor sebesar 30% pada bagian bawah gugus data. Sedangkan, metode ransac menghasilkan penduga yang berbias saat terdapat pencilan minor sebesar 25% hingga 30% baik pada bagian bawah gugus data maupun bagian atas gugus data

Dapat dilihat pula metode ransac menghasilkan lebih sedikit model yang mengandung penduga parameter berbias dibandingkan dengan metode regresi robust penduga MM. Dari 36 model yang dihasilkan oleh kedua metode, ransac hanya menghasilkan empat model yang mengandung penduga parameter berbias. Sedangkan dengan metode regresi robust penduga MM, terdapat 11 model yang mengandung penduga parameter berbias.

Daftar Pustaka

Martin A. Fischler and Robert C. Bolles, "Random Sample Consensus: A Paradigm for Model Fitting with Application to Image Analysis and Automated Cartography," Graphics and Image Processing, vol. 24, no. 6, pp. 381-395, June 1981.

Peter J. Rousseeuw and Annick M. Leroy, Robust Regression and Outlier Detection. Canada: John Wiley & Sons, Inc., 1987.

Victor J. Yohai, "High Breakdown-Point and High Effiency Robust Estimats for Regression," The Annals of Statistics, vol. 15, no. 2, pp. 642-656, Jun 1987.

52