ANALISIS REGRESI BAYES LINEAR SEDERHANA DENGAN PRIOR NONINFORMATIF
on
E-Jurnal Matematika Vol. 3, No.2 Mei 2014, 38-44
ISSN: 2303-1751
ANALISIS REGRESI BAYES LINEAR SEDERHANA DENGAN PRIOR NONINFORMATIF
Anak Agung Istri Agung Candra Iswari1, I Wayan Sumarjaya2,
I Gusti Ayu Made Srinadi3
-
1,2,3Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: 1iswari.candra@gmail.com, 2sumarjaya@unud.ac.id, 3srinadiigustiayumade@yahoo.co.id
Abstract
The aim of this study is to apply Bayesian simple linear regression using noninformative prior. The data used in this study is 30 observational data with error generated from normal distribution. The noninformative prior was formed using Jeffreys’ rule. Computation was done using the Gibbs Sampler algorithm with 10.000 iteration. We obtain the following estimates for the parameters, a0 = 1,698045 with 95% Bayesian confidence interval (0,775775; 2,626025), β = 2,999468 with 95% Bayesian confidence interval (2,948; 3,052), and σ2 = 0,697669 with 95% Bayesian confidence interval (0,375295; 1,114). These values are not very different compared to the actual value of the parameters, which are a0 = 2 and β = 3
Keywords: Bayesian regression, noninformative prior, Jeffreys’ rule, the Gibbs Sampler algorithm
-
1. Pendahuluan
Analisis regresi linear sederhana adalah salah satu cara yang dapat digunakan untuk mengetahui hubungan antara variabel bebas dan variabel terikat. Pendugaan parameter model regresi linear sederhana dapat dilakukan dengan berbagai cara tergantung dari pandangan peneliti. Dalam ilmu statistika, terdapat dua pandangan yang sering digunakan sebagai dasar dalam metode-metode untuk mengolah data (William M. Bolstad, 2007). Pandangan pertama merupakan pandangan yang umumnya sering digunakan oleh peneliti (frequentist) yakni metode yang digunakan untuk mengolah data adalah metode-metode regresi klasik seperti metode kuadrat terkecil (least square estimation) dan metode kemungkinan maksimum (maximum likelihood estimation). Pandangan kedua merupakan pandangan yang berbeda dengan para frequentist. Pandangan ini menggunakan pengetahuan dari peneliti, yang bersifat
subjektif sebagai prior yang kemudian diolah bersama data untuk memperoleh parameter regresi yang diinginkan.Pandangan kedua ini disebut pandangan Bayes.
Dalam pandangan Bayes, seseorang dapat memberikan kepercayaan awal (prior believe) terhadap suatu parameter karena adanya asumsi bahwa parameter merupakan suatu variabel acak (William M. Bolstad, 2007). Kepercayaan awal ini dapat diperbarui dengan menggunakan Teorema Bayes ketika diperoleh data amatan. Teorema Bayes menyatakan bahwa distribusi peluang posterior untuk θ terhadap data x, proporsional terhadap produk dari distribusi prior untuk θ terhadap data dan likelihood untuk θ jika diberikan data x (George E. P. Box and George C. Tiao, 1973).
Oleh karena itu, analisis regresi Bayes linear sederhana akan dipengaruhi oleh pemilihan prior dan likelihood data. Distribusi prior adalah distribusi awal parameter θ
sebelum diperolehnya data amatan (Andrew Gelman, et al., 2004). Dengan kata lain distribusi prior merupakan tingkat kepercayaan peneliti terhadap setiap nilai parameter yang mungkin. Sehingga distribusi prior akan selalu bersifat subjektif karena merupakan representasi kepercayaan peneliti.
Pemilihan prior secara umum dilakukan berdasarkan diketahui atau tidaknya informasi mengenai parameter. Jika informasi mengenai parameter diketahui, maka prior informatif, yaitu prior yang memengaruhi hasil distribusi posterior dan bersifat sangat subjektif dapat digunakan (Andrew Gelman, et al., 2004), sedangkan jika informasi mengenai parameter tidak tersedia, maka digunakan prior noninformatif yang tidak memberikan pengaruh yang signifikan terhadap distribusi posterior (George E. P. Box and George C. Tiao, 1973) sehingga informasi yang diperoleh dari data amatan bersifat lebih objektif.
Penelitian ini bertujuan untuk menerapkan analisis regresi Bayes linear sederhana dengan menggunakan prior noninformatif. Selain menduga parameter regresi, akan dilakukan inferensi dengan menggunakan selang kepercayaan Bayes.
-
2. Metode Penelitian
Model regresi linear sederhana merupakan salah satu model regresi yang sering digunakan dalam analisis regresi. Pada model ini, hanya terdapat satu variabel bebas dengan fungsi regresi linear. Disebut sederhana karena model ini hanya melibatkan satu variabel bebas dan disebut linear karena linear dalam parameter dan linear dalam variabel bebasnya [5]. Model regresi linear sederhana yang digunakan dalam penelitian ini adalah sebagai berikut:
y = a0 + βx + ε.
Data yang digunakan dalam penelitian ini adalah data yang dibangkitkan dengan menggunakan program R versi 3.0.2. Data yang dibangkitkan adalah data dengan galatyang berdistribusi normal dengan mean nol dan varians satu. Variabel bebas yang
dibangkitkan merupakan bilangan bulat positif dengan nilai 1, 2, …, 30. Variabel terikat ditentukan oleh hubungan linear antara variabel bebas dan variabel terikat. Adapun nilai parameter yang dipilih sebagai contoh simulasi dalam penelitian ini adalah α0 = 2 dan β = 3. Sehingga hubungan linear antara variabel bebas dan variabel terikat yang ditentukanadalah sebagai berikut,
y = 2 + 3% + ε
dengan ε adalah galat berdistribusi normal
yang dibangkitkan. Karena data dibangkitkan berdistribusi normal, likelihood data dinyatakan oleh:
n
1∖n Vfl
L⅛σ2)κ(-) exP∑{ 2l?y ^}
i=i
Penelitian ini menggunakan
yang maka
(1)
prior
noninformatif yang tidak memberikan
pengaruh terhadap distribusi posterior karena tidak tersedianya informasi awal mengenai parameter. Prior noninformatif yang digunakan dapat dibentuk dengan menggunakan aturan Jeffreys (Robert E. Kass and Larry Wasserman, 1996). Berdasarkan aturan Jeffreys, dari likelihood pada persamaan (1), dibentuk prior noninformatif sebagai berikut:
π(μ,σ2) = -r.
-2
(2)
Dari likelihood data pada persamaan (1) dan prior noninformatif pada persamaan (2) dibentuk distribusi posterior, yaitu:
π(μ,-2 IyJ « -2 (-) exp [∑ {" j-? '2' "^)]
= σn+2 exP[- 2-2{∑cyi - y)2 + ncy - μ)z}]
= -^ exP |2-2 {Cn - 1)s2 + n(y - μ)2}] dengan
n
s2=⅛∑c*-y)2.
i=i
Untuk memperoleh distribusi posterior marginal untuk -2, distribusi posterior
π(^, -2 ∣yj)diintegralkan terhadap μ, sehingga ^c-2Iyj k ∫ ^^expf" ^12{cn - 1)s2 +n(y-μ)2}] dμ
1/1 12π-2
' - ■ exp^ 2- n 1 ■ :^ n
, Sii ( (n —1)s2λ
k (-2) 2 exp(--——I
yang merupakan fungsi densitas untuk invers-∕2 berskala (scaled inverse-chi-square), dengan kata lain σ2∣yi~Inv — ∕2(n — 1,s2). Fungsi densitas untuk distribusi invers — ∕2 berskala memiliki fungsi densitas yang sama dengan distribusi Inv - gamma (-y-,-y^s2) (Andrew Gelman, et al., 2004).
Pendugaan nilai parameter dilakukan dengan menghitung mean dari distribusi posterior (Bradley P. Carlin and Thomas A. Louis, 2009). Salah satu metode komputasi yang dapat digunakan untuk menduga parameter adalah metode Markov Chain Monte Carlo. Metode ini membentuk suatu
rantai Markov yang digunakan sebagai sampel
Monte Carlo atau dapat dinyatakan sebagai:
Am —
1 M-B
M
∑ g(X∂
i=B+1
dengan M merupakan jumlah sampel yang dibangkitkan dan B merupakan burn-in yaitu bilangan bulat non-negatif yang menyatakan jumlah sampel awal yang harus dibuang karena terlalu bias terhadap nilai awal (Radu V. Craiu and Jeffrey S. Rosenthal, 2014).
Dalam penelitian ini digunakan algoritma Gibbs Sampler yang merupakan salah satu algoritma yang termasuk ke dalam kelas algoritma Markov Chain Monte Carlo. Algoritma Gibbs Sampler membangkitkan variabel acak dari suatu distribusi marginal tanpa harus diketahui fungsi densitasnya (Christope Andrieu, et. al. 2003). Dalam penelitian ini, algoritma Gibbs Sampler dilakukan sebanyak 10.000 kali iterasi dengan burn-in sebanyak 1.000 sampel.
-
3. Hasil dan Pembahasan
Adapun data yang dibangkitkan untuk penelitian ini merupakan data dengan galat berdistribusi normal dengan mean nol dan varians satu. Plot (a) pada Gambar 1. menunjukkan plot variabel bebas X dan variabel terikat Y dan plot (b) menunjukkan plot variabel terikat Y dengan galat. Plot antara variabel bebas X dan variabel terikat Y
menunjukkan bahwa data yang dibangkitkan memiliki hubungan yang linear antara variabel terikat dan variabel bebasnya. Sedangkan plot antara variabel terikat Y dengan galat menunjukkan bahwa galat yang dibangkitkan memiliki varians konstan.

(b) Plot Vanabel Tenkat Y dan Galat

Gambar 1. (a) Plot Variabel Bebas X dan
Variabel Terikat Y dan (b) Plot
Variabel Terikat Y dan Galat
Data variabel bebas X, galat berdistribusi normal dan variabel terikat Y yang dibangkitkan ditunjukkan oleh Tabel 1. Data yang telah dibangkitkan memiliki distribusi normal, sehingga likelihood data amatan merupakan likelihood distribusi normal seperti yang ditunjukkan oleh persamaan (1).
Tabel 1. Data Variabel Bebas, Galat, dan
Variabel Terikat yang Dibangkitkan
|
X |
ε |
K = 2 + 3% + ε |
|
1 |
-2,64753085 |
2,352469 |
|
2 |
0,45542902 |
8,455429 |
|
3 |
1,76248521 |
12,762485 |
|
4 |
-0,13762446 |
13,862376 |
|
5 |
0,13017324 |
17,130173 |
|
6 |
1,61545617 |
21,615456 |
|
7 |
-0,51863142 |
22,481369 |
|
8 |
0,30857656 |
26,308577 |
|
9 |
-2,41011001 |
26,589890 |
|
10 |
-1,32809561 |
30,671904 |
|
11 |
-0,23824422 |
34,761756 |
|
12 |
0,73449361 |
38,734494 |
|
13 |
-1,35865761 |
39,641342 |
|
14 |
-1,44779785 |
42,552202 |
|
15 |
1,06589440 |
48,065894 |
|
16 |
-1,77573754 |
48,224262 |
|
17 |
-0,42350373 |
52,576496 |
|
18 |
0,07304432 |
56,073044 |
|
19 |
-0,13094045 |
58,869060 |
|
20 |
-0,30893238 |
61,691068 |
|
21 |
1,33469871 |
66,334699 |
|
22 |
-1,94607974 |
66,053920 |
|
23 |
-1,25981853 |
69,740181 |
|
24 |
0,85737874 |
74,857379 |
|
25 |
-0,86449368 |
76,135506 |
|
26 |
0,07835018 |
80,078350 |
|
27 |
-1,82110904 |
81,178891 |
|
28 |
-0,30040502 |
85,699595 |
|
29 |
0,33639769 |
89,336398 |
|
30 |
0,93834574 |
92,938346 |
Dari data yang dibangkitkan, dilakukan analisis dengan menggunakan metode regresi Bayes linear sederhana. Pendugaan parameter dilakukan dengan menggunakan bantuan program R versi 3.0.2 dan WinBUGS versi 1.4. Luaran dari program tersebut ditunjukkan oleh Tabel 2.
Tabel 2. menunjukkan nilai dugaan untuk masing-masing parameter dengan simpangan baku dan juga kuantil-kuantilnya. Kuantil 2,5% dan 97,5% menunjukkan batas bawah dan batas atas dari selang kepercayaan Bayes
untuk masing-masing parameter.
Tabel 2. Luaran Pendugaan Nilai Parameter
|
Mean |
Simpangan Baku | ||||
|
α0 |
1,698045 |
0,464224 | |||
|
β |
2,999468 |
0,026129 | |||
|
σ2 |
0,697669 |
0,18857 | |||
|
Kuantil | |||||
|
2,5% |
25% |
50% |
75% |
97,5% | |
|
α0 |
0,775775 |
1,392 |
1,699 |
2,001 |
2,626025 |
|
β |
2,948 |
2,983 |
2,999 |
3,016 |
3,052 |
|
σ2 |
0,375295 |
0,5631 |
0,6792 |
0,81675 |
1,114 |
Nilai dugaan untuk parameterα0 = 1,698045 dengan selang kepercayaan Bayes 95% (0,775775; 2,626025). Selang kepercayaan Bayes dapat diinterpretasikan sebagai peluang nilai parameter α0 berada di antara selang (0,775775; 2,626025) adalah sebesar 95%. Nilai parameter dugaan α0 = 1,698045 menunjukkan bahwa nilai variabel terikat Y akan sama dengan 1,698045 jika nilai variabel bebasX sama dengan nol.
Nilai dugaan untuk parameter/? = 2,999468menyatakan bahwa nilai variabel terikat Yakan mengalami perubahan sebesar 2.999468 jika terjadi perubahan sebesar satu unit satuan pada variabel bebas X.Selang kepercayaan Bayes 95% (2,948; 3,052) menunjukkan bahwa peluang nilai parameter / berada di antara selang (2,948; 3,052) adalah sebesar 95%.
Nilai dugaan untuk parameters2 = 0,697669 dengan selang kepercayaan Bayes 95% (0,375295; 1,114). Dengan kata lain nilai parameter σ2 memiliki peluang sebesar 95% berada di antara selang (0,375295; 1,114).
Masing-masing nilai parameter dugaan yang diperoleh memiliki kesesuaian dengan nilai parameter yang ditentukan. Nilai dugaan dan nilai sesungguhnya dari parameter α0, yaitu dua, tidak memiliki perbedaan yang jauh. Selang kepercayaan Bayes meyakinkan bahwa nilai parameter sesungguhnya berada pada selang tersebut.
Nilai dugaan untuk parameter /memiliki nilai yang mendekati nilai parameter
sesungguhnya. Jika dibulatkan, maka nilai parameter dugaan untuk β akan sama dengan nilai parameter β yang sesungguhnya, yaitu tiga. Nilai dugaan yang mendekati nilai parameter yang sesungguhnya ini juga ditunjukkan oleh sempitnya selang kepercayaan Bayes untuk nilai parameter
dugaanβ.
Nilai dugaan untuk parameter σ2 juga tidak memiliki perbedaan yang jauh dari nilai parameter yang sesungguhnya. Varians dari galat yang dibangkitkan adalah satu, dan selang kepercayaan Bayes mencakup nilai tersebut.
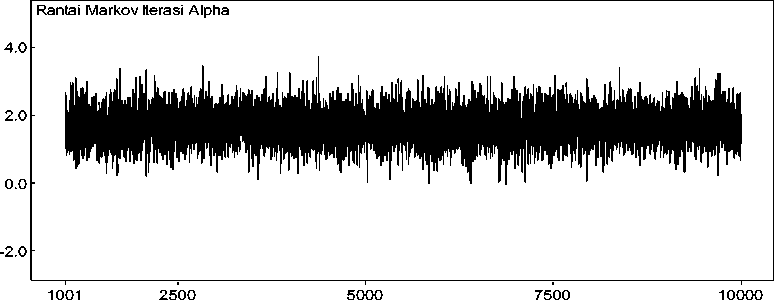
iterasi
Gambar 2a. Rantai Markov untuk Iterasi Parameter α0
Funpftt DervsitM Aipna
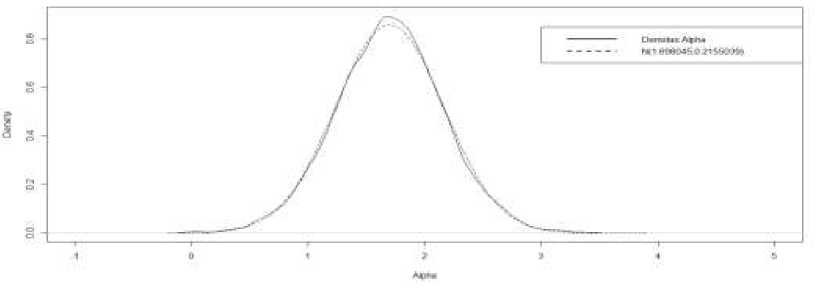
Gambar 2b. Plot Fungsi Densitas untuk α0
Gambar 2a. menunjukkan rantai Markov yang diperoleh dari iterasi Gibbs Sampler untuk parameter α0. Dari rantai Markov yang diperoleh, dapat dibentuk suatu plot fungsi
densitas untuk parameter α0 seperti yang ditunjukkan pada Gambar 2b. Plot fungsi densitas parameter α0 memiliki bentuk yang menyerupai distribusi normal.
Rantai Markov Iterasi Beta
3.2
3.0

2.8
1001 2500 5000 7500 10000
iterasi
Gambar 3a. Rantai Markov untuk Iterasi Parameter β

Gambar 3b. Plot Fungsi Densitas untuk β
Gambar 3a. menunjukkan rantai Markov yang diperoleh dari iterasi Gibbs Sampler untuk parameter β. Dari rantai Markov yang diperoleh, dibentuk suatu plot fungsi densitas
untuk parameter β seperti yang ditunjukkan pada Gambar 3b. Plot fungsi densitas parameter β juga memiliki bentuk yang menyerupai distribusi normal.
Rantai Markov Iterasi Sigma^2
2.0
1.5
1.0
0.5
0.0
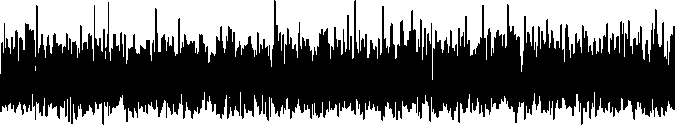
1001 2500 5000
7500
10000
iterasi
Gambar 4a.Rantai Markov untuk Iterasi Parameter σ2

Gambar 4b. Plot Fungsi Densitas untuk σ2
Gambar 4a. menunjukkan rantai Markov yang diperoleh dari iterasi Gibbs Sampler untuk parameter σ2 . Dari rantai Markov yang diperoleh, dibentuk suatu plot fungsi densitas untuk parameter σ2 seperti yang ditunjukkan pada Gambar 4b. Plot fungsi densitas parameter σ2 memiliki bentuk yang menyerupai distribusi invers-gamma. Hal ini bersesuaian dengan distribusi posterior marginal dari σ2 yang diperoleh.
-
4. Kesimpulan
Penerapan analisis regresi Bayes linear sederhana dengan menggunakan prior noninformatif selain memberikan nilai dugaan untuk parameter, juga memberikan gambaran mengenai kecenderungan distribusi dari parameter-parameter yang diduga. Hal ini dapat digunakan sebagai informasi prior jika dilakukan penelitian pada masa mendatang dengan karakteristik data yang sama.
Daftar Pustaka
William M. Bolstad. 2007. Introduction to
Bayesian Statistics, 2nd ed. New Jersey: Wiley.
George E. P. Box and George C. Tiao. 1973. Bayesian Inference in Statistical Analysis. Boston: Addison-Wesley Publishing
Company, 1973.
Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin. 2004. Bayesian Data Analysis, 2nd ed. New York: Chapman & Hall.
Andrew Gelman.2007. Statistical Modeling, Causal Inference, and Social Science. [Online].
http://andrewgelman.com/2007/07/18/inf ormative_and/
John Neter, William Wasserman, and Michael H. Kutner. 1983. Applied Linear Regression. Illnois: Richard D. Irwin.
Robert E. Kass and Larry Wasserman. 1996. "The Selection of Prior Distribution by Formal Rules," Journal of the American Statistical Association, vol. 91, pp. 13431370.
Bradley P. Carlin and Thomas A. Louis. 2009. Bayesian Methods for Data Analysis, 3rd ed. New York: Chapman & Hall.
Radu V. Craiu and Jeffrey S. Rosenthal. 2014. "Bayesian Computation Via Markov Chain Monte Carlo," Annual Review of Statistics and Its Application, vol. I, pp. 179-201.
Christope Andrieu, Nando de Freitas, Arnaud Doucet, and Michael I. Jordan. 2003. "An Introduction to MCMC for Machine Learning," Machine Learning, vol. 50, pp. 5-43.
44
Discussion and feedback