E-Jurnal Matematika Vol. 12(1), Januari 2023, pp. 44-51

DOI: https://doi.org/10.24843/MTK.2023.v12.i01.p398

ISSN: 2303-1751

PENGGUNAAN METODE PROJECTED UNIT

CREDIT PADA ASURANSI PENSIUN GABUNGAN
MODEL VASICEK DAN CIR

Farrel Willieardan1§, I Nyoman Widana2, I Putu Winada Gautama3

§Corresponding Author

ABSTRACT

Pension plan is an investment plan offered by employee company or life insurance companies to help create retirement funds. This research attempts to estimate the normal cost that participants must pay as well as the actuarial liability that must be paid by the insurance company to the participants using Projected Unit Credit method. Projected Unit Credit method uses the present value of the pension benefit and divided it by participant’s years of service. stochastic interest such as the Vasicek model and the CIR model will be used as a comparison. The result of this research is that the estimation of the normal cost and actuarial liability with the CIR model is smaller than the Vasicek model in the initial year, but the CIR model experience a greater increase than the Vasicek model which causes the normal cost and actuarial liability with the CIR model more expensive than the Vasicek model at the end of the contract. Both premiums and the actuarial liabilities increase as participants age.

Keywords: CIR, Normal Cost, Pension, Projected Unit Credit, Vasicek

  • 1.    PENDAHULUAN

Usia merupakan faktor yang dapat mempengaruhi produktivitas dan kinerja dari seorang karyawan yang bekerja di sebuah instansi atau perusahaan. Setiap pekerja tidak dapat menghindari kenyataan bahwa mereka akan memasuki usia pensiun. Kegelisahan dan kekhawatiran terdapat masa pensiun akan berdampak negatif terhadap kinerja karyawan dan kinerja perusahaan. Oleh sebab itu, perusahaan memiliki kewajiban untuk menyelesaikan permasalahan dengan mendaftarkan karyawannya ke dalam program pensiun baik yang dikelola oleh pihak perusahaan atau pihak ketiga.

Menurut Widoatmodjo (2006), setiap orang yang mengikuti program pensiun menginginkan iuran yang tidak membebani namun tetap mendapatkan manfaat yang sama. Metode Projected Unit Credit (PUC) merupakan salah satu metode yang dapat menjawab permasalahan tersebut. Menurut Chen & Matkin (2017), Metode PUC membentuk satuan unit manfaat pensiun

dengan membagikan manfaat dengan masa kerja peserta.

Islam (2016) pada penelitiannya membandingkan metode Projected Unit Credit dengan metode Attained Age Normal (AAN) pada tingkat suku bunga konstan. Hutabalian (2021) juga dengan tingkat suku bunga konstan membahas tentang metode Aggregate Cost (AC) dan Projected Unit Credit. Kedua penelitian tersebut hanya terbatas untuk status single life dan menunjukkan bahwa iuran normal yang dihasilkan metode Projected Unit Credit lebih kecil dibandingkan dengan metode lainnya. Lebih lanjut, karena pada kondisi nyata suku bunga tidak bersifat konstan, maka dalam penelitian yang dilakukan oleh Wiguna (2015) menggunakan suku bunga Vasicek dan Cox-Ingersoll-Ross (CIR) dengan perhitungan dilakukan terhadap asuransi jiwa.

Pada dasarnya, jika seseorang sudah menikah pasti ada anggota keluarga yang perlu ditanggung. Berdasarkan kondisi tersebut, penelitian ini berfokus kepada perhitungan asuransi pensiun dengan status joint life menggunakan metode Projected Unit Credit

serta menerapkan konsep suku bunga stokastik yaitu dalam penelitian ini Vasicek dan CIR untuk menghitung iuran normal dan kewajiban aktuaria. Model Vasicek dan CIR membantu peserta asuransi dan pihak asuransi dalam menghadapi tingkat suku bunga fluktuatif, karena model suku bunga akan kembali ke harga rata-rata setelah bergerak secara ekstrem.

  • 2.    METODE PENELITIAN

Penelitian ini menggunakan data yang bersifat sekunder. Data yang digunakan merupakan data suku bunga Bank Indonesia periode Agustus 2012 sampai Agustus 2022 dan Tabel Mortalita Taspen 2012.

Langkah-langkah yang dilakukan dalam penelitian ini meliputi:

1)


Menghitung suku bunga model Vasicek dan CIR dari data tingkat suku bunga Bank

Indonesia yang diperoleh melalui

(https://www.bps.go.id). Persamaan yang digunakan dalam menentukan parameter

adalah (Mariana, 2015):

^ _ n2-2n+1+U2U3-U1U3-(n-1)U4

K -- -------7-n---------------77--------

(n2-2n+1-U1U3)∆t

^

θ -


_______(n-1)U2-U1U4_______ n2-2n+1+U2U3-U1U3-(n-1)U4

(1)


(2)


,-J⅛≡G⅛^⅜+^ (3)

Dengan ¼ - ∑"=11rt, ^2 - ∑"=11 rt+1, ^3 -∑⅛-11-, dan ¼ - ∑?;?-

l 1 rt            4       t 1 γt

  • 2)    Mengkonstruksi formula baru yang diakibatkan oleh perubahan suku bunga menjadi stokastik untuk anuitas hidup, anuitas hidup berjangka, anuitas reversionary, iuran normal, dan kewajiban aktuaria.

  • 3)    Menghitung manfaat yang akan diterima oleh    peserta    asuransi    dengan

menggunakan persamaan asumsi gaji terakhir yaitu (Oktianti, 2013):

Br = w(r - e)Sr-1      (4)

  • 4)    Menghitung anuitas hidup, anuitas hidup berjangka,     anuitas     reversionary

menggunakan parameter yang diperoleh pada langkah ke-1 untuk model Vasicek dan model CIR.

  • 5)    Menentukan nilai dari Present Value Future Benefit untuk model Vasicek dan CIR.

  • 6)    Menghitung besar iuran normal yang dibayarkan oleh peserta pensiun untuk model Vasicek dan model CIR.

  • 7)    Menghitung besar kewajiban aktuaria yang akan diperoleh peserta pensiun untuk model Vasicek dan model CIR.

  • 3.    HASIL DAN PEMBAHASAN

Penerapan penggunaan metode Projected Unit Credit dengan suku bunga model Vasicek dan CIR pada contoh kasus

Contoh Kasus

Studi kasus yang digunakan dalam penelitian ini adalah sepasang suami-istri dengan suami bekerja sebagai karyawan yang mengikutsertakan istrinya dalam program asuransi pensiun mulai umur 25, 30, 35, 40, dan 45 tahun untuk peserta asuransi (suami) sampai usia pensiun 65 tahun. Kontraknya adalah jika suami dapat hidup sampai akhir kontrak, maka akan mendapatkan benefit dan jika suami meninggal sebelum kontrak berakhir dan istri masih hidup, maka istri akan mendapatkan uang pertanggungan sebesar 60% dari benefit. Diasumsikan gaji selama satu tahun terakhir sebesar Rp25,782,319. — dan (w) sebesar 2,5%.

  • 3.1    Suku Bunga Vasicek dan CIR

Estimasi parameter dalam suku bunga model Vasicek dan CIR diperoleh dengan menggunakan data suku bunga Bank Indonesia periode Agustus 2012 sampai Agustus 2022 dan dengan formula yang terdapat pada langkah 1. Jumlah data yang digunakan dianggap dapat merepresentatifkan kondisi suku bunga pada tahun selanjutnya. Dengan menggunakan persamaan (1), (2), dan (3) dan bantuan

software R 4.1.2 diperoleh estimasi parameter seperti pada Tabel 1.

10.00%

Suku Bunga Bank Indonesia

8.00%

6.00%

4.00%

2.00%

0.00%

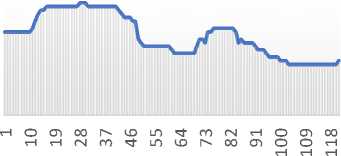
Gambar 1. Grafik Suku Bunga BI Agustus 2012 sampai Agustus 2022


Tabel 1. Hasil Estimasi Parameter Suku Bunga Vasicek dan CIR

Koefisien

Estimasi Parameter

K

0.5077925

θ

0.05781762

σ

0.2126191

(Sumber: Data Diolah 2022)

  • 3.2    Besar Manfaat Pensiun

Besar manfaat pensiun dapat dihitung menggunakan asumsi gaji terakhir peserta asuransi yaitu sebesar Rp25,782,319. — dan persamaan (4) serta w = 2,5% sebagai berikut:

Br = w(r — e)Sr-1

= 2,5%(65 — 35)(25782319)

= 19336739.3

Sehingga diperoleh besar manfaat pensiun untuk peserta usia masuk 35 tahun sebesar Rp19,336,739.3. Untuk usia lainnya dapat dilihat pada Tabel 2.

Tabel 2. Nilai Manfaat Pensiun

Usia Masuk

Manfaat Pensiun

25

Rp25.782.319

30

Rp22.559.529,1

35

Rp19.336.739,3

40

Rp16.113.949,4

45

Rp12.891.159,5

(Sumber: Data Diolah 2022)

  • 3.3    Nilai Anuitas Hidup

Anuitas hidup merupakan rangkaian pembayaran yang dibayarkan secara terus menerus atau dalam jangka waktu tertentu (bulanan, triwulan, semesteran, tahunan) selama orang tersebut masih hidup (Bowers et al, 1997). Nilai anuitas hidup model Vasicek dapat dihitung dengan persamaan

(^x = ∑i=0-P(i)vαs iPx    (5)

dengan (Hull, 2003)

P(ι)vas = exp


1 — exp(—Ki)


—i)


—


—


T" B(i) 4k

(1

r(0)(-


2


— exp (—Ki)^


Selanjutnya parameter yang telah

diestimasi pada Tabel 1 disubstitusikan kedalam persamaan P(i)vas, dapat diperoleh nilai anuitas hidup untuk model Vasicek

∞

⅛5 = ∑ P(i)vas ip65 k=0

= -W 0P65 + P(1) 1P65 + ∙∙∙ + P(46)46P65

= 1 + 0.924016308 + ∙∙∙ + 1.491E — 08

= 10,36540238

Untuk Model CIR, nilai anuitas hidup dapat dihitung dengan menggunakan

persamaan

⅛ = ∑k=0 -(i)cir ipx   (6)

dengan (Hull,2003)

2κθ

■

cir lexp(id)(κ + d) + d — k/

× exp (—


2r(0)(exp(id) — 1) exp(id)(κ + d) + d —

7)


dan

d = √k2 + 2t2,

Nilai parameter yang telah diestimasi pada Tabel 1 disubstitusikan kedalam persamaan P(i)cir, dapat diperoleh nilai anuitas hidup untuk model CIR

⅛5 = ∑∞=θP(i)cir iP65

= P(0) 0P65 + P(1 1P65 + ∙∙∙ + P(46)46P65

= 1 + 0,9263938 + ••• + 0,00000001426

= 10,41717743

Sehingga diperoleh anuitas hidup untuk suku bunga model Vasicek yaitu 10,36540238 dan untuk suku bunga model CIR yaitu 10,41717743.

  • 3.4    Nilai Anuitas Hidup Berjangka

Anuitas hidup berjangka merupakan nilai sekarang aktuaria dari sebuah pembayaran sebesar 1 satuan pada anuitas hidup diskrit yang pembayarannya dilakukan pada awal tahun kontrak dalam jangka waktu n waktu tertentu sesuai perjanjian. Nilai anuitas hidup berjangka untuk peserta usia 35 tahun dengan n=30 model suku bunga Vasicek dapat dihitung menggunakan persamaan berikut:

^^35:65-351 = ∑6=50 35 1P(i)υas iPx         (7)

^35:30T = P(0) 0p35 + P(1) 1p35 + '"

+p(29)29P35

= 1 + 0,94054358 + • +0,17891663

= 14,63862084

Untuk model suku bunga CIR, dapat dihitung

dengan menggunakan persamaan berikut: a35:65-35| = ∑6=0 35 1P(J)Cir iPx         (8)

a35:30| = P(0) 0P35 + P(1) 1P35 + -+P(29)29P35

= 1 + 0.942963782 + -+0.175207838

= 14,67074564

Diperoleh anuitas hidup berjangka untuk peserta usia 35 tahun untuk model Vasicek adalah 14,63862084 dan untuk model CIR adalah 14,67074564. Untuk usia lainnya secara ringkas dapat dilihat pada Tabel 3.

Tabel 3. Nilai Anuitas Hidup Berjangka

ae:r-e|

Vasicek

CIR

a25:40|

16,37836557

16,36818878

a30:35|

15,60830242

15,61954005

a35:30|

14,63862084

14,67074564

a40:25|

13,42040818

13,47103982

a45:20|

11,89096352

11,95493045

(Sumber: Data Diolah 2022)

  • 3.5    Nilai Anuitas Reversionary

Anuitas reversionary merupakan anuitas yang dibayarkan jika salah satu peserta asuransi meninggal dunia selama kontrak berlangsung (Futami, 1993). Nilai anuitas reversionary untuk model Vasicek dengan usia suami 35 tahun dan usia istri 30 tahun adalah

α35∣30 =∑Mp(≈)vαs(1- ip35) ip30   (9)

= P(1‰as(1 - 1P35) 1P30

+P(2)vas(1 - 2P35)2P30 + -

+P(76)vas(1 - 76P35)76P30

= 1,317016842

Nilai anuitas reversionary untuk model CIR dengan usia suami 35 tahun dan usia istri 30 tahun dapat dihitung dengan persamaan sebagai berikut

a35∣30 = ∑∞=ιp(0cir(1 - iP35) iP30   (10)

= P(1)cir(1 - 1P35) 1P30

+P(2)cir(1 - 2P35) 2p30 + -

+P(76)cir(1 - 76P35)76P30

= 1,281330601

Diperoleh nilai anuitas yang dibayarkan jika salah satu peserta asuransi meninggal dunia selama kontrak berlangsung dengan peserta suami berusia 35 tahun dan istri berusia 30

tahun untuk model Vasicek adalah 1,317016842 dan untuk model CIR adalah 1,281330601. Untuk usia lainnya lebih ringkas disajikan pada Tabel 4.

Tabel 4. Nilai Anuitas Reversionary

Usia x|y

Vasicek

CIR

a25|20

0,8885404

0,8556472

a30|25

1,08797424

1,053177

a35|30

1,317016842

1,281330601

a40|35

1,57260841

1,53743

a45|40

1,847423385

2,14015961

(Sumber: Data Diolah 2022)

  • 3.6    Perhitungan Present Value Future

Benefits (PVFB)

Nilai PVFB dalam penelitian ini dapat dihitung dengan menggunakan persamaan

(PVFB)x = BrVr-∖-xPxar + 0.6(⅛⅛y)  (11)

Persamaan (11) diperoleh dengan menjumlahkan kewajiban yang dibayarkan oleh pihak suami ditambahkan dengan kewajiban yang dibayarkan untuk kondisi bila suami meninggal sebelum kontrak selesai, istri tetap mendapatkan manfaat. Dengan memasukan nilai anuitas seumur hidup dan anuitas reversionary, dapat dihitung nilai PVFB untuk peserta berusia 35 tahun untuk model Vasicek sebagai berikut:

65(PVFB)45vas = (19336739,3)P(65 - 45)vas

× 65-45P45(10,3 6 5 4 0 2 38)

+0,6 (19336739,3)

× (1,317016842)

= 72.796.233,28

Untuk model CIR, dapat dihitung dengan menggunakan persamaan

65(PVFB)45cir = (19336739,3)P(65 - 45)cir

× 65-45P45(10,4 1 7 1 77 43)

+0,6 (19336739,3)

× (1,317016842)

= 72.236.133,47

Diperoleh nilai sekarang manfaat pensiun yang akan diterima peserta asuransi pada tahun valuasi 45 tahun dengan peserta berusia 35 tahun untuk model Vasicek adalah Rp72.796.233,28 dan untuk model CIR adalah Rp72.236.133,47. Untuk usia lainnya lebih ringkas disajikan pada Tabel 5.

Tabel 5. Nilai PVFB model Vasicek dan CIR

Usia (x, y)

6≡φyFB)45vαs

65(PyFB)45cir

(25,20)

90.433.374,23

89.729.781,55

(30,25)

81.828.682,88

81.187.264,45

(35,30)

72.796.223,28

72.236.133,47

(40,35)

63.134.681,45

62.672.840,47

(45,40)

52.633.355,40

54.800.203,34

(Sumber: Data Diolah 2022)

  • 3.7    Perhitungan Iuran Normal

Besarnya iuran normal yang dibayarkan oleh peserta asuransi dipengaruhi oleh masa kerja peserta. Persamaan umum untuk

menghitung iuran normal dalam penelitian ini

adalah

(NC)x


1

~  ~ (BrP(T - x)r-xpx^-r)

τ — e

0.6(BrΛχ∣y) ⅛r-e∣


+


(12)


Iuran normal untuk suami berusia 35 tahun

dan istri berusia 30 tahun dengan model Vasicek dengan tahun valuasi 45 tahun adalah sebagai berikut:

1

<nc)4⅛ = 65-35 (βrp(65 — 45)““

× 65-45p45^^65)

+ 0,6(Br^35∣3θ)

⅝5^5-35∣

1

= —(57516146,52)

+ (1043820,106)

= 2.961.024,99

Untuk model CIR, iuran normal dapat dihitung sebagai berikut:

1

(NC)45cir = ξ5T^5 (β^(65 — 45U

× 65-45p45^^65)

0,6(Br<⅞5∣3θ)

⅝5⅛5-35∣

1

= —(57370080,03)

+(1013312,738)

= 2.925.648,74

Sehingga diperoleh iuran normal peserta asuransi dengan suami usia 35 tahun dan istri 30 tahun pada tahun ke-10 (45 tahun) untuk model Vasicek adalah Rp2.961.024,99 dan

untuk model CIR adalah Rp2.925.648,74. Untuk usia lainnya secara ringkas dapat dilihat pada Tabel 6.

Tabel 6. Nilai Normal Cost model Vasicek dan CIR

Usia (x, y)

NCvas

NCclr

(25,20)

Rp2.756.432,63

Rp2.720.998,56

(30,25)

Rp2.860.709,92

Rp2.825.007,21

(35,30)

Rp2.961.024,99

Rp2.925.648,74

(40,35)

Rp3.050.148,02

Rp3.015.772,75

(45,40)

Rp3.118.895,37

Rp3.296.993,43

(Sumber: Data Diolah 2022)

Untuk lebih jelas, disajikan iuran normal tahunan yang harus dibayarkan oleh peserta asuransi dalam bentuk grafik seperti pada gambar 2 sampai gambar 6.

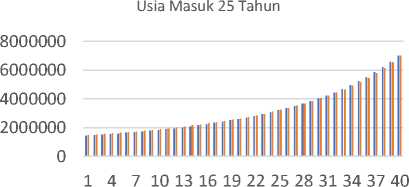
CIR Vasicek


Gambar 2. Grafik Iuran Tahunan Peserta Usia Masuk 25 Tahun

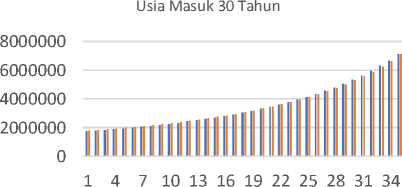
CIR Vasicek

Gambar 3. Grafik Iuran Tahunan Peserta Usia Masuk 30 Tahun

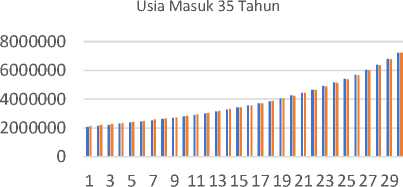
CIR Vasicek


Gambar 4. Grafik Iuran Tahunan Peserta Usia Masuk 35 Tahun

CIR Vasicek


Gambar 5. Grafik Iuran Tahunan Peserta Usia

Masuk 40 Tahun

Usia Masuk 45 Tahun

8000000

6000000

4000000

2000000

0

1   3   5   7   9  11 13 15 17 19

CIR Vasicek

Gambar 6. Grafik Iuran Tahunan Peserta Usia Masuk 45 Tahun

Berdasarkan gambar di atas, dapat dilihat bahwa pada usia masuk 25, 30, 35, dan 40 tahun pada tahun-tahun awal pembayaran, besarnya biaya yang harus dibayarkan jika menggunakan model suku bunga CIR lebih murah dibandingkan dengan model suku bunga Vasicek, namun terlihat bahwa besarnya biaya jika menggunakan model suku bunga CIR mengalami peningkatan yang cukup besar yang menyebabkan biaya dengan model suku bunga Vasicek lebih murah pada akhir kontrak. Sedangkan pada usia masuk 45 tahun, dapat dilihat bahwa pembayaran tahunan dengan

menggunakan suku bunga model CIR sampai akhir kontrak lebih mahal dibandingkan dengan model suku bunga Vasicek hal ini dikarenakan faktor dari anuitas reversionary sebagai pengali pada suku bunga CIR lebih besar daripada suku bunga Vasicek.

  • 3.8    Perhitungan Kewajiban Aktuaria

Kewajiban aktuaria merupakan dana yang dikumpulkan oleh pihak penanggung yang nantinya digunakan sebagai pembayaran manfaat pensiun kepada pihak tertanggung di masa depan (Dickson dkk, 2013). Persamaan umum dalam menghitung kewajiban aktuaria pada penelitian ini yaitu:

x — e

(AL)x        BrP(r  χ)1—χPχO-r

r — e

+ ^0,6(Brax∣y)        (13)

“e:r-e|

Kewajiban aktuaria dengan peserta berusia 35 tahun untuk suami dan 30 tahun untuk istri

dengan model Vasicek pada tahun valuasi 45 tahun sebagai berikut:

45

(AL')45vas = 65


—


—


35

35 BrP(65   45Jvas 65-45p45a65

, a35:45-35|

+ ________0,6(Bra35|30)

a35:65-35|

10

= —(57516146,52)

7,776527755 z

+ U63∞20T(152800^

= 27.289.344,87

Untuk model CIR, kewajiban aktuaria yang harus dibayarkan oleh pihak asuransi adalah:

45 — 35

(AL)45cir = ⅛5T⅛BrP(65 — 45~)cir

l a35:45-35| × 65-45p45a65 + ■■        ^

a35:65-35|

× 0,6(Bra35|30)

10

= 30 (57370080,03) ι 7,83549492 + 14,67074564

= 27.063.166,82

Sehingga diperoleh kewajiban aktuaria yang harus disiapkan oleh pihak asuransi dengan     model     Vasicek     adalah

Rp27.289.344,87 dan untuk model CIR adalah Rp27.063.166,82. Untuk usia lainnya,

kewajiban aktuaria secara ringkas disajikan pada Tabel 7.

Tabel 7. Nilai kewajiban aktuaria model Vasicek dan CIR

Usia (χ,y)

ALvas

ALdr

(25,20)

Rp48.583.256

Rp48.165.281,23

(30,25)

Rp38.477.272,52

Rp38.150.659,59

(35,30)

Rp27.289.344,87

Rp27.063.166,82

(40,35)

Rp14.620.440,57

Rp14.491.948,66

(45,40)

Rp 0,-

Rp 0,-

(Sumber: Data Diolah 2022)

Pada dasarnya, pada metode Projected Unit Credit, kewajiban aktuaria akan terus meningkat setiap tahunnya dengan tahun x = e nilai kewajiban aktuarianya adalah Rp 0,-. Hal ini dikarenakan pada tahun x = e, peserta belum memiliki cadangan manfaat karena baru melakukan iuran pada tahun tersebut. Untuk lebih memahami, dapat dilihat contoh kewajiban aktuaria yang diperoleh untuk peserta dengan usia masuk 25 tahun pada Gambar 7.

Usia Masuk 25 Tahun

300000000

200000000

100000000

0

1 3 5 7 9 1113151719212325272931

CIR Vasicek

Gambar 7. Grafik Kewajiban Aktuaria Peserta Usia Masuk 45 Tahun

  • 4.    SIMPULAN DAN SARAN

    • 4.1    Simpulan

Perhitungan iuran normal dan kewajiban aktuaria menggunakan metode PUC untuk status joint life dengan menggunakan model suku bunga Vasicek dan CIR mengalami peningkatan setiap tahunnya. Dari hasil perhitungan, diperoleh bahwa iuran normal dan kewajiban aktuaria untuk suku bunga model CIR lebih kecil daripada model Vasicek pada awal tahun, namun pada akhir tahun kontrak

iuran normal dan kewajiban aktuaria untuk suku bunga model CIR menjadi lebih besar daripada model Vasicek. Hal ini dikarenakan model CIR mengalami peningkatan yang lebih besar daripada model Vasicek seiring bertambahnya tahun pada iuran normal yang dibayarkan oleh peserta asuransi dan kewajiban aktuaria yang dibayarkan oleh pihak asuransi. .

  • 4.2    Saran

Penelitian ini hanya menggunakan satu metode perhitungan aktuaria yaitu Projected Unit Credit untuk menghitung iuran normal dan kewajiban aktuaria, disarankan pada penelitian selanjutnya menggunakan dua atau lebih metode perhitungan aktuaria seperti Frozen Initial Liability dan Individual Level Premium dengan tetap menggunakan suku bunga stokastik.

DAFTAR PUSTAKA

Bowers, N. L., Gerber, H. U., Hickman, J. C.,

Jones, D. A., & Nesbit, C. J. (1997).

Actuarial Mathematics. Illinois(US):The Society of Actuaries.

Chen, G. & Matkin, D. (2017). Actuarial

Inputs and the Valuation Of Public Pension Liabilities and Contribution Requirements: A Simulation Approach. Public Budgeting & Finance, 37(1), pp.68-87.

Dickson, D. C., Hardy, M. R., & Waters, H.

R. (2013). Actuarial Mathematic for Life Contingent Risk. United State of America: Cambridge University Press.

Futami, T. (1993). Matematika Asuransi Jiwa

Bagian I. Tokyo: Oriental Life Insurance

Cultural Development Center.

Hull, J. C. (2003). Option, Future, and Other

Derivatives, 5th ed. United States of America: Prentice Hall.

Hutabalian, S.V., Nyoman, I.N., dan Harini,

  • L.P.I. (2021). Penggunaan Metode Projected Unit Credit dan Aggregate Cost Pada Asuransi Pensiun Normal. E-Jurnal Matematika, 10(4), pp.209-214.

Islam, M.E.N., Wilandari, Y., dan Suparti.

  • (2016). Perhitungan Pembiayaan Dana

Pensiun Dengan Metode Attained Age

Normal dan Projected Unit Credit. Jurnal Gaussian, 5(3), pp.505-514.

Mariana, E., Apriliani, E., dan Surjanto, S.D. (2015). Estimasi Parameter pada Model Suku Bunga Cox Ingersoll Ross (CIR) Menggunakan Kalman Filter untuk Menentukan Harga Zero Coupon Bond. Jurnal Sains dan Seni ITS, 4(2), pp.23373520.

Oktiani, I. (2013). Perhitungan Aktuaria untuk    Manfaat    Pensiun-Normal

Menggunakan Metode Projected Unit Credit dan Entry Age Normal. Skripsi. Bogor: Institut Pertanian Bogor.

Widoatmodjo, S. (2006). Cara Mudah Merancang Sendiri Pensiun Anda. Jakarta: Elex Media Komputindo.

Wiguna, I.M.W., Jayanegara, K., dan Widana, I.N. (2019). Perhitungan Premi Asuransi Joint Life Dengan Model Vasicek dan CIR. E-Jurnal Matematika, 8(3), pp.246-252.

51