GRAPH TANGGA DAN SIFAT-SIFATNYA

E-Jurnal Matematika Vol. 12(3), Agustus 2023, pp. 177-181

DOI: https://doi.org/10.24843/MTK.2023.v12.i03.p416

ISSN: 2303-1751

GRAPH TANGGA DAN SIFAT-SIFATNYA

Mareta Sekar Larasati^1§, Luh Putu Ida Harini², I Wayan Sumarjaya³

¹Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

²Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

³Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Ladder Graph is one type of connected and simple graph that has its own uniqueness. The aim of this research is to find the k-deficiency of points in the spanning tree in the ladder graph. Calculation of k-deficiency is carried out for each additional step, starting from the second ladder ( L2), up to the n^th Ladder (Ln). Calculations are based on a representative spanning tree on each ladder. In the end, we get a number pattern from the second ladder onwards which is then proven by mathematical induction, for the calculation of each step up the ladder. In this study, the pattern of k-deficiency points on the ladder graph was obtained.

Keywords: Ladder Graph, k-defisiensi, Mathematical Induction

• 1.    PENDAHULUAN

Matematika dapat diaplikasikan ke dalam berbagai bidang ilmu, di antaranya bidang biologi, kimia, teknologi, dan komunikasi. Salah satu cabang ilmu matematika yang dapat diaplikasikan pada bidang-bidang tersebut adalah teori graph. Salah satu materi yang dibahas dalam teori graph adalah k-defisiensi titik. Menghitung total k-defisiensi titik dari pohon merentang pernah diterapkan pada graph terhubung (Anggraini, 2011).

Graph telah dikembangkan melalui beberapa riset pada tahun 1960-an. Aplikasi graph pada kehidupan manusia antara lain: komputer, rangkaian pada listrik, peta, penggambaran jaringan komunikasi, dan lainnya. Salah satu bagian yang dipelajari dari teori graph adalah tentang pohon, pohon merentang pada graph serta k-defisiensi titik. Dalam berbagai bidang ilmu, konsep pohon merupakan salah satu konsep yang dapat mendukung pada penerapan graph. Kirchoff (1824—1887) mengembangkan teori pohon untuk diterapkan dalam jaringan listrik.

Terdapat berbagai macam jenis graph, salah satunya adalah graph tangga (ladder graph). Graph Tangga ini adalah salah satu graph yang memiliki pola dalam jumlah edge dan titiknya di setiap pertambahan anak tangganya. Kurniawan (2009) juga melakukan penelitian terhadap graph tangga

yaitu tentang pelabelan harmonis gabungan graph tangga segitiga LS_n, dengan graph tangga variasi X_n.

Beberapa penelitian lainnya mengenai graph tangga antara lain sebagai berikut. Hanani (2014) menilai ketakteraturan total edge dari graph tangga permata. Pada penelitian tersebut mendapatkan hasil bahwa bobot edge dari graph tangga memiliki nilai yang berbeda.

Slamin (2014) menilai ketakteraturan total edge dari graph tangga (stair graph). Lebih lanjut Slamin (2014) mendapatkan bahwa dari formulasi bobot edge pada graph tangga, terlihat bahwa bobot berbeda pada tiap edge sederhana yang memiliki keunikan tersendiri, yaitu memiliki suatu pola pada jumlah titik dan edgenya. (Aprilia, 2011) suatu graph sederhana yang dinotasikan dengan L_n dengan n adalah banyak anak tangga dapat disebut dengan graph tangga. Graph tangga dapat diilustrasikan seperti bentuk tangga pada suatu bangunan.

Pada graph tangga L_n, banyak titiknya 2n, dan banyak edgenya adalah 3n — 2, berlaku untuk setiap pertambahan anak tangganya. Berdasarkan keunikan graph tangga pada pola banyak titik dan edgenya, penulis tertarik untuk mengkaji lebih lanjut penentuan nilai k-defisiensi titik dari pohon merentang pada graph tangga di setiap anak

tangga graph.

• 2.    METODE PENELITIAN

Kajian pustaka merupakan metode penelitian pada penelitian ini yaitu dengan mengumpulkan dan mengkaji referensi berupa skripsi, buku, jurnal maupun tulisan dari perpustakaan dan internet. Langkah-langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:

• 1.    Menggambar graph yang akan digunakan untuk mencari k-defisensi titik.

• 2.  Mencari setiap kemungkinan pohon

merentang yang terdapat pada graph tersebut. Pohon merentang merupakan graph yang tidak memiliki cycle dalam suatu graph.

• 3.  Setelah didapatkan setiap kemungkinan

pohon merentang lalu menentukan derajat titik.

• 4.  Menentukan k-defisiensi titik pada graph

tangga di setiap pertambahan anak tangganya dengan rumus:

deg_c(V_i) - degτ(V_i) — k          (1)

dengan deg_G merupakan jumlah derajat titik pada graph tangga dan deg_τ adalah derajat titik pada pohon merentangnya.

• 5.    Kemudian menemukan pola rumusnya.

• 6.    Membuktikan pola rumus k-defisiensi titik yang telah ditentukan.

• 3.    HASIL DAN PEMBAHASAN

Penelitian ini mengambil sample untuk graph tangga L₂ sampai L₄. Berikut merupakan perhitungannya:

• 3.1    Pohon Merentang dan k-defisiensi Titik

pada Graph Tangga L₂

Pada subbab ini untuk mengawalinya dicari pohon merentang pada graph tangga. (Chartrand dan Zhang,  2005) Graph

H dikatakan subgraph dari graph G, dapat dituliskan H ⊆ G, jika V(H) ⊆ V(G) dan E(H) ⊆ E(G).

Selanjutnya dengan mencari         k-

defisiensi titik pada graph tangga, dan yang terakhir yaitu membuktikan secara umum menggunakan induksi matematika. Graph tangga L₂ dapat digambarkan seperti pada gambar 2.1 sebagai berikut:

¹⁷I v₂

V₄ V₃

Gambar 1. Graph Tangga L₂

Anak tangga dari graph tangga L₂ adalah (v₁, v₂) dan (v₂, v₃). Pada graph tangga L₂, dicari terlebih dahulu pohon merentangnya, dapat diilustrasikan pada gambar 2:

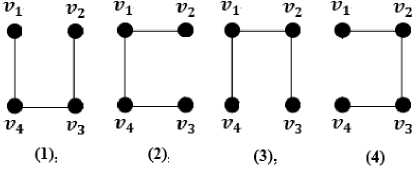
Gambar 2. Pohon Merentang Graph

Tangga L2 (1), (2), (3), dan (4)

Graph tangga L₂ banyak kemungkinan

pohon merentang yang dapat dicari dengan menggunakan rumus kombinasi, dengan jumlah edge graph tangga L₂  yaitu 4

dikurangi satu edge agar membentuk pohon merentang. Sehingga rumusnya adalah C^ = 4!4.3!

—7---- —— 4.

1!(4-1)!1!3!

Selanjutnya dicari k-defisiensi titik. yang pertama menentukan banyak derajat masing-masing titiknya dengan melihat pada graph berapa jumlah edge pada titiknya. Banyak kemungkinan pohon merentang pada L₂ adalah 4 pohon. Diambil 1 pohon untuk contoh perhitungan, yaitu Pohon Merentang Lz(X)'-

• 1.    Titik V₁ memiliki derajat 1

• 2.    Titik V₂ memiliki derajat 1

• 3.    Titik V₃ memiliki derajat 2

• 4.    Titik V₄ memiliki derajat 2

Nilai k dari k-defisiensi titik ditentukan menggunakan persamaan rumus (1):

• 1.  Titik V₁ nilai k — 2-1 — 1

• 2.  Titik V₂ nilai k — 2-1 — 1

• 3.    Titik V₃ nilai k—2-2—0

• 4.    Titik V₄ nilai k — 2-2 — 0

Dengan demikian k-defisiensi titik dari graph tangga L₂ adalah 1 + 1 + 0 + 0 — 2.

DOI: https://doi.org/10.24843/MTK.2023.v12.i03.p416

• 3.2    Pohon Merentang dan k-defisiensi Titik

Graph Tangga L₃

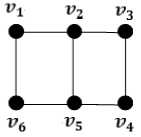
Graph tangga L₃ dapat ditunjukkan dengan gambar 3.

Gambar 5. Bukan Pohon Merentang dari L₃

Gambar 3. Graph Tangga L₃

Titik yang terdapat di L₃ berjumlah 6, dengan anak tangganya adalah O₁,v₆)^v₂,v₅) dan (v₃,v₄). Terdapat 4 titik dengan banyak edge yang terhubung

sebanyak 2 dan 2 titik dengan 3 edge terhubung.

Salah satu rumus yang dapat mengetahui jumlah pohon merentang pada graph tangga L₃ dengan menggunakan rumus kombinasi. Untuk mendapatkan pohon merentang di graph     tangga     L₃ yaitu     dengan

menghilangkan dua edgenya dari total edge nya, dan didapat rumusnya      C₂⁷ =

7.6.5!

• -^-    = 21. Graph tangga L₃ memiliki pohon merentang pada gambar 4 yaitu:

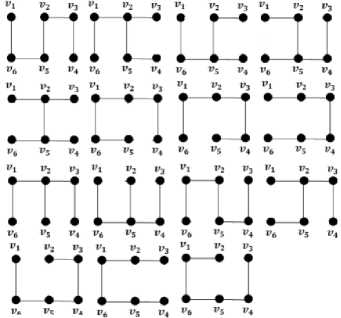
Gambar 4. Pohon Merentang Graph Tangga L₃

Jika

diperhatikan dari rumusnya,

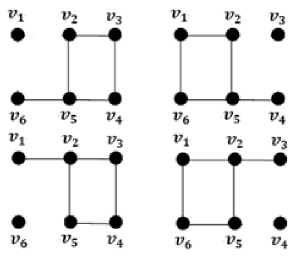
didapatkan C₂⁷ = ⁷⁶⁵ = 21. Tetapi untuk di graph tangga L₃ terdapat pengambilan dua edge yang tidak dapat membentuk pohon merentang, antara lain:

• a.    Dua edge yang terhubung di titik berderajat dua (ada 4 kali).

Kemudian terlihat pada Gambar 5. merupakan bukan pohon merentang karena terdapat titik terasing dan adanya cycle.

• b.    Sepasang edge yang berhadapan dan bukan merupakan anak tangga (ada 2 pasang).

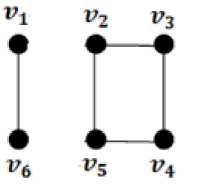
Gambar 6. Bukan Pohon Merentang dari L₃ bagian a

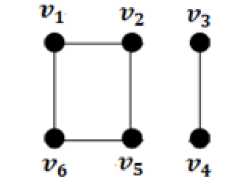
Gambar 7. Bukan Pohon Merentang dari L₃ bagian b

Kemudian terlihat pada Gambar 6 dan 7 merupakan bukan pohon merentang karena terdapat edge yang tidak terhubung dan masih mengandung cycle. Jadi pohon merentang yang bisa dibentuk dari graph L₃ adalah 21 — 4 — 2 = 15 pohon dan bentuk geometrisnya dapat dilihat pada Gambar 4. Terdapat beberapa jenis pohon merentang pada graph tangga L₃, salah satunya pada gambar 8 yaitu:

Gambar 8. Perwakilan pohon merentang graph tangga L3

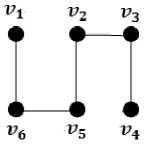
Nilai k dari k-defisiensi titik ditentukan menggunakan persamaan rumus (1) dan didapatkan untuk perhitungan k-defisiensi titik:

• 1. Untuk titik V₁, k = 2 — 1 =1

• 2. Untuk titik V₂, k = 3 — 2 =1

• 3. Untuk titik V₃, k = 2 — 2 =0

• 4. Untuk titik V₄, k = 2 — 1 =1

• 5. Untuk titik V₄, k = 3 — 2 =1

• 6. Untuk titik V₄, k = 2 — 2 =0

Dengan demikian k-defisiensi titik dari graph

tangga L₃ adalah 1 + 1 + 0 + 1 + 1 + 0 = 4

• 3.3 Pohon Merentang dan k-defisiensi

Titik Graph Tangga L₄

Graph tangga L₄ dapat ditunjukkan dengan gambar berikut:

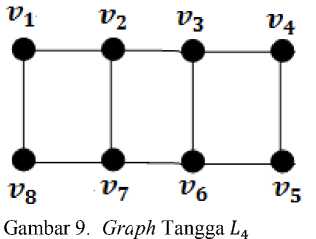
Untuk mendapatkan pohon merentang di graph tangga L₄ yaitu dengan menghilangkan tiga edge nya, dan didapatkan C∙1⁰ = ¹°₇9^,'⁷' = 120. Tetapi untuk di graph tangga L₃ terdapat pengambilan  dua edge yang tidak dapat

membentuk pohon merentang, antara lain: a. Dua edge yang terhubung di titik paling

ujung dan masing-masing satu edge selain di tengah dan bukan anak tangga (ada 8 bentuk) b. Satu anak tangga, dan sepasang selain anak

tangga yang saling sehadap (ada 12 bentuk) c. Ketiga edge yang terhubung dalam satu titik

(ada 4 bentuk)

• d.    Dua anak tangga, dan satu edge yang terhubung dalam dua titik (ada 4 bentuk selain tengah)

• e.    Satu pasang edge yang sehadap bukan anak tangga dan satu edge selain anak tangga lainnya (ada 12 bentuk)

• f.    Edge yang berada di titik berderajat dua dan satu anak tangga yang tidak berdekatan dengan dua edge tadi (ada 8 bentuk)

Berdasarkan alibi-alibi yang didapat, dengan demikian jumlah pohon merentangnya adalah 120 — 8 — 12 — 4 — 4 — 12 — 8 = 72. Graph tangga L₄ memiliki pohon merentang yaitu:

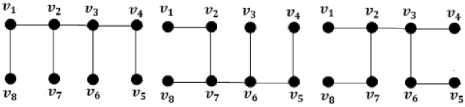
(1)            (2)              (3)

Gambar 10. Beberapa Perwakilan Pohon

Merentang Graph Tangga L₄

Nilai k dari k-defisiensi titik ditentukan menggunakan persamaan rumus (1) dan didapatkan untuk perhitungan k-defisiensi titik: 1.  Untuk titik V₁ nilai k = 2 — 2 = 0

• 2.  Untuk titik V₂ nilai k = 3 — 3 =0

• 3.  Untuk titik V₃ nilai k = 3 — 3 =0

• 4.  Untuk titik V₄ nilai k = 2 — 2 =0

• 5.  Untuk titik V₅ nilai k = 2 — 1 =1

• 6.  Untuk titik V₆ nilai k = 3 — 1 =2

• 7.  Untuk titik V₇ nilai k = 3 — 1 =2

• 8.  Untuk titik V₈ nilai k = 2 — 1 =1

Dengan demikian k-defisiensi titik dari graph tangga L₄ adalah 0 + 0 + 0 + 0 + 1 + 2 + 2 + 1 = 6.

Selanjutnya dari hasil perhitungan didapat bahwa:

• 1.    Untuk k-defisiensi titik graph tangga L₂ adalah 2

• 2. Untuk k-defisiensi titik graph tangga L₃

adalah 4

• 3. Untuk k-defisiensi titik graph tangga L₄

adalah 6

Dengan demikian diperoleh konjektur:

Untuk graph tangga L_n didapat pola 2(n — 1) dengan n ≥ 2, n ∈ N. Untuk membuktikan pola tersebut berlaku setiap n ≥ 2, n ∈ N dibuktikan dengan induksi matematika.

• 1.    Basis Induksi

Untuk n = 2 diperoleh k-defisiensi titik tangga L₂ ≡ 2(n — 1) = 2

• 2.    Langkah induksi

Diasumsikan benar k-defisiensi titik pada graph tangga untuk k anak tangga,     yaitu     L_fe ≡ 2(k — 1).

Dibuktikan bahwa k-defisiensi titik pada graph tangga untuk k + 1 anak tangga adalah L_fe+1 ≡ 2k.

Perhatikan bahwa L_n ≡ 2(n — 1) untuk n = k + 1 diperoleh

Lfe+1 ≡ 2(k + 1 — 1)

≡ 2k + 2 — 2

≡ 2k — 2 + 2 = 2k

Dengan demikian k-defisiensi titik pada graph tangga, untuk n anak tangga (L_n) adalah 2(n- 1) dengan n ≥ 2,n ∈ N terbukti benar.

• 4.    KESIMPULAN DAN SARAN

Berdasarkan pembahasan dari penelitian ini, diperoleh kesimpulan bahwa k-defisiensi titik pada graph tangga, untuk n anak tangga (L_n) adalah 2(n — 1) dengan n ≥ 2,n ∈ N. Sehingga jika k-defisiensi titik pada graph tangga untuk k anak tangga, yaitu L_k ≡ 2(k — 1) , maka untuk k + 1 anak tangga

diperoleh L_k+1 ≡ 2k. Untuk k-defisiensi pada setiap anak tangganya ialah:

• 1.    Graph tangga L₂ memiliki k-defisiensi titik 2(2 - 1) = 2.

• 2.    Graph tangga L₃ memiliki k-defisiensi titik 2(3 - 1) = 4.

• 3.    Graph tangga L₄ memiliki k-defisiensi titik 2(4 - 1) = 6.

Berlaku hingga k-defisiensi titik pada graph tangga Ln.

Penulis menyarankan untuk perhitungan k-defisiensi titik pada graph tangga, bisa mencoba perhitungan pada jumlah edge nya. Mungkin akan ditemukan pola seperti yang dilakukan pada perhitungan terhadap titik di penelitian ini.

Pada penulisan ini hanya menghitung    k-

defisiensi titik untuk jenis graph tangga saja.

Jika ingin melanjutkan penelitian, dapat menambahkan graph jenis lain. Apakah dalam graph jenis lain terdapat pola pada perhitungan k-defisiensi titik pada graph tersebut atau tidak.

DAFTAR PUSTAKA

Anggraini, Puspita. 2011. Total k-defisiensi Titik dari Pohon Merentang Suatu Graph Terhubung. Malang: Universitas Islam Negeri Maulana Malik Ibrahim

Aprilia, Ira. 2011. Pelabelan Total Super (a, d)-Sisi     Antimagic     Pada     Graph

Tangga.Tidakdipublikasikan      (Skripsi).

Jember: Universitas Jember.

Chartrand, G., Zhang, P. 2005. A First Course in Graph Theory. Dover Publication: New York

Hanani, Hilmiyah. 2014. Nilai Ketakteraturan Total Sisi dari Graph Tangga Permata. Jember: Universitas Jember

Kurniawan, Haris. 2009. Spectrum Graph Komplit (Kn), n≥ 2 dan n ∈ N. UIN Malang: Malang

Slamin. 2014. Total Vertex Irregularity Strength of Ladder Related Graphs. Jember: Universitas Negeri Jember.

181