PENENTUAN KONTRAK OPSI TIPE EROPA MENGGUNAKAN MODEL SIMULASI VARIANCE GAMMA (VG)
on
E-Jurnal Matematika Vol. 12(3), Agustus 2023, pp. 182-186
DOI: https://doi.org/10.24843/MTK.2023.v12.i03.p417
ISSN: 2303-1751
PENENTUAN KONTRAK OPSI TIPE EROPA MENGGUNAKAN MODEL SIMULASI VARIANCE GAMMA (VG)
Ni Kadek Lani Pitrayani1§, Komang Dharmawan2, I Nyoman Widana3
“1Program Studi Matematika, Fakultas MIPA-Universitas Udayana” [Email: lanipitra@gmail.com] “2Program Studi Matematika, Fakultas MIPA-Universitas Udayana” [Email: k.dharmawan@unud.ac.id]
“3Program Studi Matematika, Fakultas MIPA-Universitas Udayana” [Email: nwidana@yahoo.com] §Corresponding Author
ABSTRACT
Options are used as a hedge against stock price uncertainty brought on by unstable stock prices fluctuation. The price of an option contract can be determined using a variety of approaches, one of which is the Variance Gamma. The purpose of this study is to compare the Black Scholes method with the Variance Gamma simulation model to determine the European call option contract price. The first thing that needs to be done is to figure out the moment variance gamma method. These parameters were used as initial values to get an idea of what the parameters that will be used in the simulation will be like. The European call option contract's price is calculated using the simulation results, which are then compared to the Variance Gamma simulation model and the Black Scholes model for the European call option contract. This study shows that the European call option contract's price, which was calculated using the Variance Gamma simulation, is less expensive than the Black Scholes contract's price.
Keywords: European type Option, Variance Gamma, Black Scholes
Kontrak Opsi antara dua pihak untuk menjual atau membeli saham pada harga yang telah ditentukan dikenal sebagai opsi. Opsi dapat digunakan sebagai lindung nilai terhadap ketidakpastian harga saham yang disebabkan oleh volatilitas atau pergerakan harga saham yang selalu berubah-ubah.
Volatilitas adalah seberapa jauh harga saham bergerak selama periode waktu tertentu. Volatilitas yang tinggi menimbulkan ketidakpastian yang akan diperoleh. Sehingga menyebabkan pergerakan harga saham yang cenderung selalu berubah-ubah. Model gerak Brown biasanya digunakan untuk mengukur volatilitas dengan asumsi bahwa volatilitas merupakan konstan dan terdistribusi secara normal. Adanya volatility clustering atau volatilitas yang tinggi menjadi salah satu penyebab tidak terpenuhinya asumsi normalitas, sehingga menyebabkan bentuk distribusi data memungkinkan menjadi asimetris dan memiliki keruncingan dibandingkan dengan distribusi normal. Hal ini membuat kinerja model Gerak Brown tidak cukup baik untuk menggambarkan dinamika harga aset, sehingga model harga
saham yang cocok untuk menggambarkan saham yang asimetris dan memiliki keruncingan yaitu model Variance Gamma (Hoyyi et al., 2021).
Menurut Hoyyi et al., (2021) Variance Gamma merupakan model yang mampu menangani data keuangan dengan sangat baik, karena dalam model Variance Gamma melibatkan parameter untuk menggambarkan varians, kurtosis dan skewness.
Untuk harga kontrak opsi Eropa, tujuan dari penelitian ini adalah untuk membandingkan model Black Scholes dan model Variance Gamma.
Jenis data penelitian yang dilakukan adalah berupa data sekunder yaitu data harga penutupan saham PT Unilever Indonesia (UNVR.JK) dalam jangka waktu dua tahun dari tanggal 1 Januari 2020 sampai dengan 1 Januari 2022 yang bersumber dari https://finance.yahoo.com/.
Tahapan-tahapan dalam menentukan harga kontrak opsi call tipe Eropa dengan model
simulasi Variance Gamma, yaitu:
-
1. Mengumpulkan data harga penutupan saham harian PT Unilever Indonesia melalui http://www.yahoo.finance.com.
-
2. Menghitung nilai statistik deskriptif
3. Menghitung nilai parameter awal yaitu
μ, σ, v, dan θ dengan persamaan:
(1)
μ
M
-
θ
-
4. Mengestimasi parameter Variance Gamma mengacu pada penelitian yang dilakukan oleh Loregian et al. (2012)
-
5. Melakukan simulasi harga saham dengan Variance Gamma menggunakan persamaan
sτ - S^+^+^ (2)
-
6. Menghitung harga kontrak Opsi call Tipe
C — e rτmaks(Sτ — K, 0) (3)
-
7. Menghitung harga opsi dengan model Black Scholes menggunakan persamaan
C - S0N(d1) — Ke~rτN(d2) (4)
-
8. Membandingkan harga kontrak opsi tipe Eropa yang didapat melalui model Variance Gamma dengan Black Scholes
3. HASIL DAN PEMBAHASAN
Analisis data ini berbantuan dengan Microsoft Excel dan program Matlab R2021a. Data yang digunakan adalah data penutupan harga saham harian PT Unilever Indonesia (UNVR.JK). Selama dua tahun di mulai dari tanggal 1 Januari 2020 sampai 1 Januari 2022 yang diperoleh dari https://finance.yahoo.com/ dengan total jumlah data yaitu 489.
Eropa menggunakan persamaan
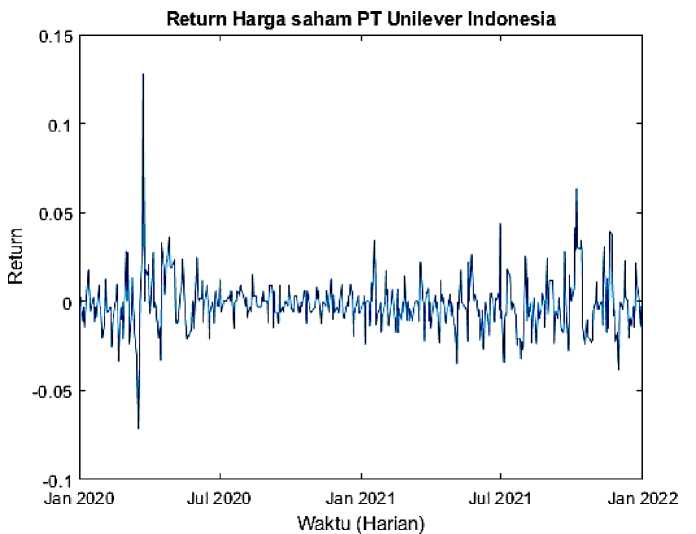
Gambar 1. Plot data return saham PT Unilever Indonesia periode 1 Januari 2020-1 Januari 2022
Gambar 1 menunjukkan bahwa plot data return terdapat pengelompokkan volatilitas (volatility clustering) pada bulan April 2020.
Langkah selanjutnya yaitu menentukan statistik deskriptif yaitu mean, variance, skewness dan kurtosis dari nilai return dengan bantuan program Matlab, sehingga dapat disajikan pada Tabel 1.
Tabel 1. Nilai Statistik Deskriptif
|
Statistik Deskriptif |
Nilai |
|
M |
-0,0015 |
|
V |
0,0153 |
|
S |
1,3274 |
|
K |
14,8009 |
Nilai statistik deskriptif return memiliki ekor yang gemuk, ditunjukkan dengan nilai kurtosis yang relatif tinggi sebesar 14.8009, seperti terlihat pada Tabel 1. hal ini disebabkan banyaknya data ekstrem yang disebabkan oleh volatility clustering.
Pada Tabel 1, masukkan nilai statistik deskriptif yang diperoleh. sehingga diperoleh nilai parameter awal dari Variance Gamma sebagai berikut:
Tabel 2. Nilai Parameter Awal Variance Gamma
|
Parameter Awal |
Nilai parameter awal variance gamma |
|
P |
-3,8070 |
|
σ |
0,0159 |
|
v |
1,9438 |
|
θ |
3,4362 |
Hasil dari parameter yang telah diperoleh dari Tabel 2 digunakan untuk melakukan Estimasi parameter Variance Gamma yang mengacu pada penelitian Loregian et al., (2012) dengan bantuan program Matlab.
Estimasi parameter variance gamma dapat disajikan pada Tabel 3.
Tabel 3. Estimasi Parameter Variance Gamma
|
Parameter Optimal |
Estimasi Parameter Variance Gamma |
|
P |
-0,0031 |
|
σ |
0,0490 |
|
v |
1,5282 |
|
^^a θ |
3,7722 |
Hasil dari estimasi parameter yang didapatkan dari Tabel 3 digunakan untuk melakukan simulasi Variance Gamma menggunakan persamaan (2) dengan S0 sebesar Rp 4.110,00 dalam jangka waktu tiga bulan. Simulasi harga saham (St) dihitung dengan bantuan program Matlab disajikan pada Gambar 2.
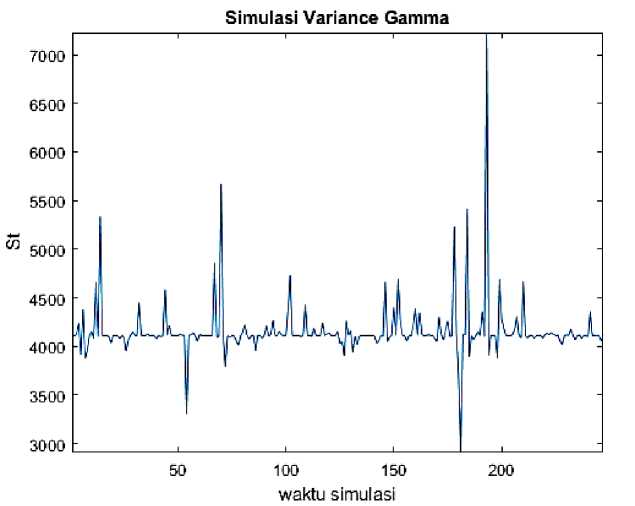
Gambar 1. Grafik simulasi harga saham
Pada Gambar 2 menampilkan simulasi variance gamma yang dilakukan 1 kali, karena simulasi variance gamma membangkitkan bilangan acak, terlihat pada pergerakan harga saham mengikuti proses stokastik yang menyebabkan nilai volatilitasnya berubah secara acak, sehingga dilakukan beberapa kali simulasi kemudian dirata-ratakan dan diperoleh
nilai harga saham (St).
Selanjutnya melakukan perhitungan kontrak opsi call tipe Eropa menggunakan simulasi variance gamma pada persamaan (3) memiliki nilai T selama 0,25 tahun, dan nilai r sebesar 3,5%. Menggunakan simulasi gamma varians untuk menentukan harga opsi Eropa, dilakukan simulasi sampai 10000000 kali dalam program
Matlab. Nilai yang diperoleh menjadi lebih stabil dengan simulasi tambahan. Tabel 4 menunjukkan hasil penggunaan model Variance Gamma untuk mengetahui harga kontrak opsi call Eropa.
Berdasarkan Tabel 4 dilihat dengan menggunakan model Variance Gamma, semakin besar nilai K atau harga pelaksanaan. maka harga opsi call yang diperoleh akan semakin kecil.
Tabel 4. Harga Kontrak Opsi Call tipe Eropa dengan Variance Gamma
|
N |
Harga Opsi Call Eropa dengan Variance Gamma (Rp) | ||||
|
K = 3900 |
K = 4000 |
K = 4110 |
K = 4200 |
K=4300 | |
|
100 |
336,7405 |
258,3237 |
159,3027 |
148,6907 |
123,5124 |
|
500 |
335,6149 |
257,6766 |
156,3892 |
144,9452 |
121,1802 |
|
1000 |
334,5146 |
246,2493 |
153,7738 |
132,0822 |
117,1751 |
|
5000 |
322,1792 |
235,1358 |
149,6235 |
131,9418 |
114,4640 |
|
10000 |
334,8411 |
235,2348 |
139,4286 |
126,6402 |
110,0246 |
|
100000 |
322,5288 |
231,8880 |
137,9375 |
118,9750 |
105,7338 |
|
1000000 |
322,5050 |
231,7660 |
137,6544 |
118,5623 |
105,4014 |
|
10000000 |
322,4999 |
231,4156 |
137,1169 |
118,2410 |
105,2015 |
Selain itu harga opsi call yang diperoleh terlihat belum stabil sampai simulasi ke-10000, dalam hal ini harga opsi call yang diperoleh masih berubah-ubah dan pada simulasi ke-100000 harga opsi call yang diperoleh secara berturut-turut tetap dan tidak berubah saat
simulasi dijalankan, sehingga pada saat 10000000 simulasi diberhentikan.
Harga kontrak opsi tipe Eropa kemudian dibandingkan dengan model simulasi Black-Scholes dengan Variance Gamma pada Tabel 5.
Tabel 5. Perbandingan Harga Kontrak Opsi tipe Eropa menggunakan simulasi Variance Gamma dengan Black Scholes
|
Harga Pelaksanaan |
Opsi call tipe Eropa (Rp) | |
|
Black Scholes |
Simulasi Variance Gamma | |
|
K=3900 |
337,3194 |
322,4999 |
|
K=4000 |
274,4656 |
231,4156 |
|
K=4110 |
214,5313 |
137,1169 |
|
K=4200 |
172,6836 |
118,2410 |
|
K=4300 |
133,4913 |
105,2015 |
Pada Tabel 5 dapat dilihat perbedaan nilai yang dihasilkan dalam harga kontrak opsi call tipe Eropa menggunakan simulasi Variance Gamma dan model Black Scholes. Jika menggunakan model Black Scholes maka harga yang dihasilkan lebih tinggi dari harga yang dihitung menggunakan simulasi Variance Gamma terutama untuk jumlah simulasi yang banyak dilakukan, hal ini dikarenakan pendekatan harga kontrak opsi dalam menggunakan simulasi Variance Gamma lebih
fair karena dilakukan simulasi berkali-kali dan lebih banyak parameter yang dilibatkan diantaranya μ, σ, v, dan 0, sedangkan pada model Black Scholes hanya melibatkan dua parameter yaitu volatilitas (σ) dan rata-rata return (μ).
4. KESIMPULAN DAN SARAN
Berdasarkan hasil yang diperoleh dari perhitungan harga kontrak opsi call tipe Eropa
menggunakan model variance gamma memberikan hasil yang lebih murah dibandingkan dengan harga kontrak opsi call tipe Eropa menggunakan model Black Scholes. Hal ini dilihat dari banyaknya parameter variance gamma yang dilibatkan seperti μ, σ, v, dan 0. Sedangkan pada model Black Scholes hanya melibatkan dua parameter yaitu volatilitas (σ) dan rata-rata return (μ).
Untuk peneliti selanjutnya disarankan untuk membandingkan hasil variance gamma dengan Normal Inverse Gaussian.
DAFTAR PUSTAKA
Hoyyi, A., Rosadi, D., & Abdurakhman.
(2021). Daily Stock Prices Prediction Using Variance Gamma Model. Math. Comput. Sci, 11(2), 1888–1903.
https://doi.org/10.28919/jmcs/5469.
Loregian, A., Mercuri, L., & Rroji, E. (2012). Approximation of the variance gamma model with a finite mixture of normals. Statistics and Probability Letters, 82(2), 217–224.
https://doi.org/10.1016/j.spl.2011.10.004.
186
Discussion and feedback