APLIKASI COX PROPORTIONAL HAZARD PADA SINTASAN PASIEN ASMA
on
E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 53-57
DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p360
ISSN: 2303-1751
APLIKASI COX PROPORTIONAL HAZARD PADA SINTASAN PASIEN ASMA
Ni Nengah Rika Puspita1§, Made Susilawati2, Ni Luh Putu Suciptawati3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: puspitarikaa@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
§Corresponding Author
ABSTRAK
Asthma is defined as a chronic inflammatory disease of the respiratory tract. Since 2013, Bali ranks sixth out of thirty three provinces in Indonesia for the most asthma patient. This study has a purpose to examine the influential factors on the cure rate of asthma patients and determine the best model using the stepwise method. To determine the survival rate of asthma patients, a statistical method that involves censored data is used by applying the Cox Proportional Hazard regression. The data used in this study were medical records of asthma patients who were hospitalized at the Wongaya Regional General Hospital in Denpasar for the period January 1st, 2019 to April 2nd, 2020. The analysis of this study discovered that significant variables for the survival of asthma patients were age and disease.
Keywords: Asthma, Cox Proportional Hazard Regression, Survival rate
Asma dikenal sebagai penyakit pada saluran pernapasan yang disertai peradangan kronis dimana bersifat fluktuatif (hilang timbul). Setiap tahunnya, separuh dari seluruh pasien asma melakukan rawat inap dan kunjungan kebagian gawat darurat (Rengganis, 2008). Menurut RISKESDAS (2013) penyakit asma di Bali menempati urutan keenam dari tiga puluh tiga provinsi di Indonesia.
Salah satu metode statistika yang dapat menduga faktor-faktor yang memengaruhi tingkat kesembuhan pasien asma yaitu analisis sintasan (survival analysis). Pada analisis sintasan secara khusus mengacu pada kejadian sebagai kegagalan atau suatu pengalaman negatif individu seperti kematian, terjadinya penyakit, atau kesembuhan. Analisis sintasan parametrik merupakan salah satu analisis sintasan yang distribusinya diikuti oleh sebaran data waktu sintasan tersebut.
Penelitian yang telah dilakukan tentang regresi cox diantaranya Dewi dkk (2018) yang meneliti tentang Sintasan Pasien Diabetes Melitus dengan Regresi Cox Proportional Hazard dan Wahyuni dkk. (2019) yang meneliti tentang analisis sintasan parametrik pada pasien stroke dengan pendekatan distribusi Weibull.
Sehingga perlu diketahui faktor yang memengaruhi tingkat kesembuhan pada pasien asma.
Kleinbaum & Klein (2005) menyatakan bahwa data tersensor memiliki pengaruh yang besar dalam analisis sintasan yang mana konsep data tersensor itulah yang akan membedakan analisis sintasan dengan analisis statistika lainnya. Data tersensor merupakan data yang menjelaskan informasi tentang waktu sintasan individu namun belum ada kepastian terkait lamanya sintasan dari individu tersebut
Dalam analisis sintasan pemodelan yang sangat sering digunakan yaitu Cox Proportional Hazard karena asumsi proposional pada fungsi hazardnya, yang mana pengecekan asumsi proporsional hazard dapat dilakukan dengan plot log minus log. Model regresi cox biasanya terdapat pada situasi individu mengalami kegagalan untuk bertahan hidup disuatu waktu yang mana satu atau lebih variabel bebas memengaruhinya (Collect, 1994).
Adapun tujuan dari penelitian ini adalah untuk mengetahui faktor-faktor yang mempunyai pengaruh pada kesembuhan pasien asma di RSUD Wangaya Denpasar dengan menggunakan aplikasi Cox Proportional Hazard.
Model regresi Cox Proportional Hazard bisa diaplikasikan untuk mengetahui keterkaitan antara periode sintasan suatu individu dengan variabel berpengaruh lainnya (Lee & Wong, 2003). Data yang digunakan adalah data sekunder yang diperoleh dari data rekam medik pasien asma yang pernah menjalani rawat inap di RSUD Wangaya Denpasar pada periode 1 Januari 2019 hingga 2 April 2020. Penelitian ini mengacu pada penelitian Respitasari (2016) yang menyatakan bahwa lama pasien asma menjalani rawat inap rata-rata 2-4 hari. Hal ini berkaitan dengan menentukan status data tersensor dalam penelitian ini. Status tersensor dalam studi ini yaitu penderita asma yang dirawat inap namun belum dinyatakan sembuh dalam waktu 2-4 hari dikatakan tersensor dan pasien asma yang menjalani rawat inap sudah dinyatakan sembuh dalam 2-4 hari maka dikatakan tidak tersensor. Adapun variabel yang digunakan adalah variabel dependen yaitu data tersensor dan variabel independent yaitu jenis kelamin, usia dan penyakit yang menyertai.
Faktor-faktor yang bisa menghambat kesembuhan penderita asma dimodelkan dengan Cox Proportional Hazard yang mana digunakan untuk menentukan model yang paling baik. Metode stepwise digunakan dalam penentuan tersebut. Metode stepwise merupakan kombinasi dari forward regression dan backward regression untuk mengatasi multikolinearitas.
Beberapa tahapan analisa data dalam studi ini, antara lain :
-
1. Merekapitulasi data sekunder pasien asma yang menjalani rawat inap berdasarkan data tersensor
-
2. Melakukan identifikasi karakteristik dari data penderita asma yang sedang menjalani rawat inap.
-
3. Mengetahui peluang kesembuhan penderita asma yang sedang dirawat inap dengan melakukan pendugaan. Pendugaan yang dilakukan yaitu penduga fungsi sintasan dan penduga fungsi hazard.
-
4. Pengaplikasian plot log minus log dalam pengujian asumsi Proportional Hazard untuk mengetahui lamanya sintasan pada tiap variabel bebas.
-
5. Pengujian multikolinearitas yang mana dalam pengambilan keputusan
memerhatikan nilai tolerance beserta nilai VIF yaitu nilai tolerance <0,10 dan nilai VIF > 5 yang mengindikasikan bahwa
variabel bebas tersebut memiliki korelasi yang kuat atau terdapat multikolinearitas.
-
6. Pengujian rasio likelihood secara simultan serta pemilihan model dengan
memperhatikan nilai yang berubah pada model. Perubahan nilai tersebut diperoleh dengan membandingkan nilai antara model tanpa variabel bebas dan model dengan variabel bebas.
-
7. Melakukan uji signifikan parameter secara parsial. Pengujian ini dijalankan guna menyelidiki lebih dalam terkait pengaruh variabel independen dengan variabel dependen.
-
8. Penentuan model terbaik yaitu dengan model regresi Cox Proportional Hazard. Dalam hal ini penentuan model terbaik akan dilakukan menggunakan metode stepwise.
-
9. Interpretasi hasil.
Pengolahan data dalam menduga fungsi sintasan dan fungsi hazard, menguji asumsi proporsional hazard dengan plot log minus log, menguji rasio likelihood, menguji signifikansi parameter serta menentukan model terbaik, yang semua dibantu dengan menggunakan software SPSS.
Kaplan-Meier mengintregrasikan informasi dari semua pengamatan yang tersedia, baik berupa data tersensor maupun data tak tersensor, dengan mempertimbangkan setiap titik dalam waktu sebagai serangkaian langkah yang ditetapkan oleh waktu sintasan dan waktu tersensor. Dalam hal ini metode kaplan-meier digunakan dengan membuat plot dari masing-masing penduga.
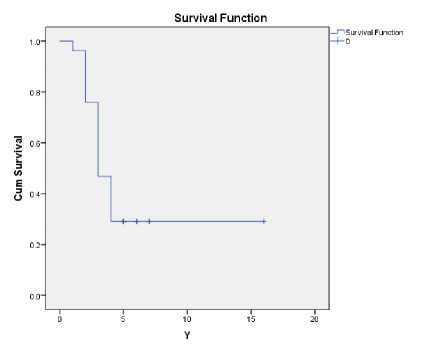
Gambar 1. Grafik Plot Fungsi Sintasan
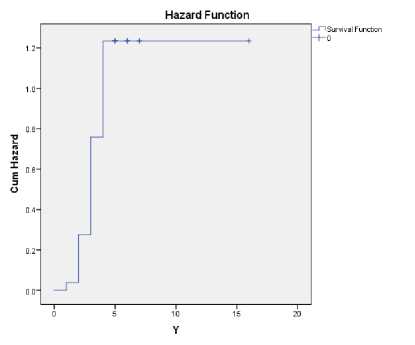
Gambar 2. Grafik Plot Fungsi Hazard
Pada Gambar 1 merupakan grafik plot fungsi sintasan yang dimana terlihat bahwa grafik cenderung menurun setiap waktu yang artinya semakin lama pasien asma menjalani rawat inap maka peluang untuk tidak sembuh menurun. Gambar 2 menunjukkan grafik plot fungsi hazard terlihat hal yang berbeda yaitu grafik cenderung meningkat setiap waktu yang artinya resiko pasien asma untuk tidak sembuh mengakibatkan lama waktu pasien asma dirawat semakin meningkat.
-
3.2 Regresi Cox Proportional Hazard
-
a. Asumsi Pemodelan Cox Proportional
Hazard
Asumsi pemodelan Cox Proportional Hazard dapat dilakukan dengan membuat grafik log minus log (LML) untuk mengetahui proporsional waktu sintasan dari masing-masing variabel bebas sehingga dapat menentukan variabel-variabel apa saja yang dapat dimodelkan dengan regresi Cox Proportional Hazard. Berikut ini grafik plot log minus log(LML) dari tiga variabel independen yang digunakan:
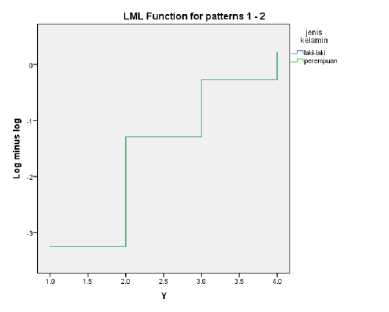
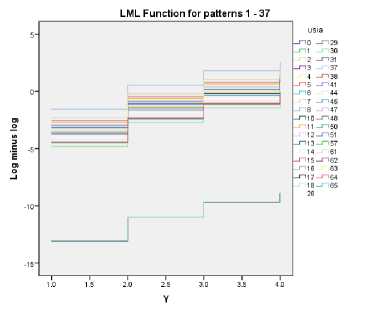
LML Function for patterns 1 - 2
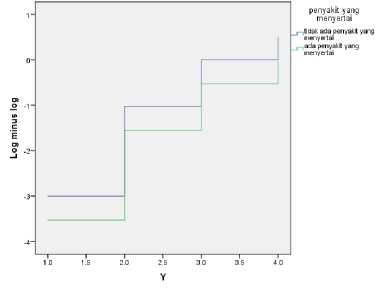
Dari ketiga grafik di atas dapat ditarik kesimpulan bahwa ketiga variabel independen proporsional terhadap waktu serta dapat digunakan dalam model regresi Cox Proportional Hazard.
Keterkaitan di antara variabel bebas dalam model regresi bisa diketahui melalui pengujian multikolinearitas. Pengujian multikolinearitas yang menyimpang bisa diketahui dengan cara memperhatikan nilai tolerance dan VIF dari setiap variabel bebas.
Tabel 1. Hasil Pengujian Multikolinearitas
|
Collinearity statistics | ||
|
Tolerance |
VIF | |
|
X1 |
0,946 |
1,057 |
|
X2 |
0,957 |
1,045 |
|
X3 |
0,968 |
1,033 |
Sumber: Data diolah,2020
Dapat dilihat pada Tabel 1 nilai tolerance seluruh variabel independen > 0,10. Sementara itu nilai VIF seluruh variabel independen <10. Sehingga, dapat disimpulkan tidak terdapat gejala multikolinearitas artinya hasil pengujian
pada data tersebut dapat dikatakan reliabel atau terpercaya.
Pengujian rasio likelihood diterapkan dalam pemilihan model yang baik sehingga dampak dari variabel bebas secara simultan bisa terlihat jelas dan kepentingan relatif dari setiap variabel bebas bisa ditentukan. Pengujian rasio likelihood ini guna untuk melihat nilai —2 log likelihood yang berubah dalam model tanpa variabel bebas dan model dengan variabel bebas dibandingkan dengan nilai —2 log likelihoodnya.
Tabel 2. Hasil Analisis Univariat
|
Model Dengan Variabel yang Disertakan |
-2 log likelihood |
Perubahan |
Nilai signifikansi |
|
Tanpa Variabel |
454,246 |
- |
- |
|
Jenis Kelamin |
453,909 |
0,337 |
0,562 |
|
Usia |
414,743 |
39,502 |
0,316 |
|
Penyakit yang Menyertai |
450,340 |
3,906 |
0,048 |
Sumber: Data diolah,2020
Pada Tabel 2. terdapat hanya satu variabel independen yang signifikan yaitu penyakit yang menyertai. Menurut Guerra et al. (2002), resiko mengalami penderitaan asma 3 kali dimiliki oleh orang dewasa yang memperoleh pasien rinitis dengan dan tanpa atopi. Untuk pasien rinitis dengan kandungan Imunoglobulin E merupakan antibodi yang dihasilkan sistem imun dalam hal ini melonjak akan berhadapan dengan resiko asma 5 kali lebih banyak sehingga bisa disimpulkan dari penelitian Guerra et al. (2002) bahwa penyakit lain selain asma memiliki pengaruh yang sangat besar.
Langkah berikutnya pengujian
signifikansi parameter secara parsial. Analisis ini mempunyai tujuan agar diketahui pengaruh variabel bebas pada variabel respon. Hipotesis yang digunakan yaitu:
H0 : βj = 0, dengan j = 1,2,...., 3
H1 : βj ≠ 0, dengan j = 1,2,...., 3
Dalam pengujian signifikansi parameter akan digunakan uji Wald. Dalam penelitian ini
digunakan a = 0,05, diperoleh bahwa Xy > ^ι-o,o5 = 3,841 yang berarti tolak H0.
Tabel 3. Hasil Pengujian Parsial Data Waktu Sintasan Penderita Asma
|
Variabel Bebas |
βj |
SE(βj) |
Statistik Uji Wald |
p-value |
Keputusan |
|
Jenis Kelamin |
-0,122 |
0,276 |
0,195 |
0,65 8 |
Terima H0 |
|
Usia |
-0,012 |
0,007 |
2,793 |
0,09 5 |
Terima H0 |
|
Penyakit yang Menyertai |
-0,584 |
0,273 |
4,598 |
0,03 2 |
Tolak H0 |
Sumber: data diolah, 2020
Berdasarkan Tabel 3. Terdapat pengaruh nyata secara parsial dari suatu variabel bebas dan juga terdapat variabel bebas yang tidak memberi dampak nyata pada waktu sintasan pasien asma pada kesembuhan 5%. Variabel Yang dimaksud dengan variabel bebas dengan pengaruh nyata secara parsial yakni variabel penyakit yang menyertai
Penentuan model terbaik menggunakan metode stepwise. Metode stepwise adalah kombinasi dari prosedur eliminasi langkah mundur/ backward dan prosedur eliminasi langkah maju/forward. Stepwise ini juga biasanya digunakan untuk mengatasi multikolinearitas.
Tabel 4. Penentuan Model Terbaik dengan Stepwise
|
B |
Exp(B) |
Sig. | |
|
Constant |
2,610 |
0,000 | |
|
Usia |
0,026 |
1,026 |
0,017 |
|
Penyakit yang menyertai |
0,963 |
2,619 |
0,024 |
Sumber: Data diolah, 2020
Ditinjau dari Tabel 4, diperoleh model Cox proportional hazard yang paling baik yakni:
H(t,X) = h0(t)e0,026χ2e0,963^3
Pada persamaan di atas, terdapat nilai exp(β) yang menunjukan nilai resiko kegagalan (hazard ratio) dari masing-masing variabel independen yang dapat diinterpretasikan dengan merujuk
pada nilai koefisien dan eksponen dari koefisien sebagai berikut:
-
a. Hazard ratio yang diperoleh menunjukan bahwa variabel usia memiliki nilai eksponen dari koefisiennya sebesar 1,026. Karena 1,026 > 1 maka dapat diartikan bahwa untuk setiap kenaikan usia individu sebesar satu unit maka nilai tingkat kegagalan (belum sembuh) semakin meningkat.
-
b. Hazard ratio yang diperoleh menunjukkan bahwa variabel penyakit yang menyertai memiliki nilai eksponen dari koefisiennya sebesar 2,619 dengan yang tidak memiliki penyakit menyertai sebagai referensinya. Karena 2,619 > 1 maka dapat diartikan
bahwa pasien asma yang memiliki penyakit menyertai mempunyai resiko lebih besar untuk belum sembuh dibandingkan dengan pasien asma yang tidak memiliki penyakit yang menyertai.
Hasil serta pembahasan yang telah diperoleh dalam studi ini dapat disimpulkan dari ketiga variabel independen yang digunakan untuk memodelkan tingkat kesembuhan pasien asma hanya terdapat dua variabel independen yang berpengaruh nyata yaitu usia dan penyakit yang menyertai.
Penelitian selanjutnya disarankan untuk memperhatikan kelengkapan informasi dari data rekam medik, sehingga tidak menghambat penelitian terutama dalam hal perolehan informasi yang mendukung dalam pengolahan data serta penelitian berikutnya diharapkan mampu melakukan pengembangan penelitian dengan metode statistika yang berbeda dan dalam pengujian asumsi cox proportional hazard lebih diperjelas secara analitik agar pembaca lebih mudah memahami.
DAFTAR PUSTAKA
Collect. (1994). Modelling Survival Data in Medical Research (first; C. Chatfield & J. V. Zidek, eds.). https://doi.org/10.1007/978-1-4899-3115-3
Dewi, I. A. P. R., Suciptawati, N. L. P., & Tastrawati, N. K. T. (2018). Aplikasi Regresi Cox Proportional Hazard Pada Sintasan Pasien Diabetes Melitus. E-Jurnal Matematika, 7(3), 278.
https://doi.org/10.24843/mtk.2018.v07.i03.p 215
Guerra, S., Sherrill, D. L., Martinez, F. D., & Barbee, R. A. (2002). Rhinitis as an
independent risk factor for adult-onset
asthma.Journal of Allergy and Clinical Immunology,109(3),419–425.
https://doi.org/10.1067/mai.2002.121701
Kleinbaum, D. G., & Klein, M. (2005). Statistics for Biology and Health (Second).New York:Springer Science+Business Media, Inc.
Lee, J., & Wong, D. (2003). Statistical Methods for Survival Data Analysis (Third). New York: John Wiley & Sons, Inc.
Rengganis, I. (2008). Diagnosis dan tatalaksana asma bronkial. Maj Kedokt Indonesia, 58, 444–451.
Respitasari, R. (2016). Tingkat Kontrol Pasien Asma di Poli Spesialis Paru B Rumah Sakit Paru Jember. Jember: Repository
Universitas Jember.
RISKESDAS. (2013). Riset Kesehatan Dasar. https://doi.org/10.1517/13543784.7.5.803
Wahyuni, N. M. S., Sumarjaya, I. W., &
Suciptawati, N. L. P. (2019). Analisis Sintasan Parametrik Pada Pasien Stroke Dengan Pendekatan Distribusi Weibull. E-Jurnal Matematika, 8(1), 55.
https://doi.org/10.24843/mtk.2019.v08.i01.p 235
57
Discussion and feedback