IMPROVED EXPONENTIAL APPROACH METHOD DAN ZERO SUFFIX METHOD DALAM MENENTUKAN SOLUSI OPTIMAL PADA MASALAH TRANSPORTASI
on
E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 23-30
DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p356
ISSN: 2303-1751
IMPROVED EXPONENTIAL APPROACH METHOD DAN ZERO SUFFIX METHOD DALAM MENENTUKAN SOLUSI OPTIMAL PADA MASALAH TRANSPORTASI
Istiqomah1§, Ni Ketut Tari Tastrawati2, Luh Putu Ida Harini3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: Istiqomahh48@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: tastrawati@unud.ac.id ]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ballidah@unud.ac.id ]
§Corresponding Author
ABSTRACT
The problem of transportation is a problem of distributing goods from several sources to several destinations with the aim of minimizing shipping costs. Distribution activities in a company sometimes experience problems in transportation problems so that a model is needed to determine the optimal distribution using the transportation model. This study aims to determine the route of distribution of beras putri sejati 25 kg in UD Sinar Jaya Abadi so that optimal expenses can be obtained using improved exponential approach and zero suffix method. Based on the calculation results, both methods produce the same three distribution path. The first distribution channel is from Agen Monang Maning to Toko Mekar Sari and Subur Jaya. The second distribution line from the Agen Gatsu Barat to UD Mas Ayana and Toko Dharma. The third line from agen Gianyar to UD Sinar Wangi, Toko Sari Artha, UD Amertha, and Toko Ayu Mega with optimal distribution costs of Rp 1.575.815.00. The difference or efficiency of the total costs incurred in the distribution before and after optimization by UD Sinar Jaya Abadi Rp 499,190.00 or 24%.
Keywords : Distribution, Improved Exponential Approach, Zero Suffix, Transportations model
Beras merupakan sumber makanan pokok masyarakat Indonesia. Menurut Badan Pusat Statistik tahun 2017 kebutuhan masyarakat Indonesia akan beras meningkat setiap tahunnya. Hal ini mengakibatkan banyak perusahaan pendistribusian beras bersaing untuk dapat memberikan kualitas produk beras yang baik dengan harapan mengeluarkan biaya distribusi minimum sedemikian hingga dapat memperoleh keuntungan maksimum. Harapan tersebut dapat dicapai apabila sebuah perusahaan mempertimbangkan beberapa faktor salah satunya persoalan transportasi.
Persoalan transportasi merupakan salah satu persoalan pemrograman linear dalam menentukan cara pendistribusian suatu barang dari sumber ke tujuan dengan mengalokasikan barang yang ada pada sumber sedemikian rupa hingga kebutuhan pada tujuannya terpenuhi (Kertiasih, 2012). Adapun beberapa aspek yang harus diperhatikan saat melakukan proses pendistribusian yaitu kualitas produk, biaya
distribusi, dan rute yang akan ditempuh (Karundeng dkk., 2018). Namun tidak semua perusahaan dapat memperhatikan hal tersebut sehingga untuk mengatasi permasalahan tersebut dapat digunakan model transportasi.
Pada model transportasi terdapat beberapa metode tak langsung dan metode langsung. Metode langsung merupakan metode yang dapat memperoleh solusi optimal tanpa harus mencari solusi awal. Beberapa metode tersebut di antaranya yaitu metode zero neigbouring, zero suffix, metode exponential approach, metode asm dan sebagainya. Metode-metode tersebut telah menemukan solusi yang optimal dalam masalah transportasi yang seimbang. Akan tetapi pada masalah transportasi yang tidak seimbang belum tentu dapat menemukan solusi yang optimal (Septiana dkk., 2017)
Terdapat pengembangan dalam memperbaiki kelemahan tersebut salah satunya yaitu pada metode exponential approach. Pengalokasian jumlah barang pada metode tersebut bergantung pada angka nol yang
muncul pada tabel transportasi. Pada kasus transportasi tidak seimbang akan terdapat penambahan variabel dummy dengan asumsi biaya distribusi sebesar nol yang berpengaruh terhadap hasil optimalnya. Sehingga dikembangkan menjadi metode improved exponential approach (Hidayat, 2016).
Sehubungan dengan penerapan metode transportasi, adapun menurut Hasan (2012) menggunakan metode zero suffix telah didapatkan biaya distribusi yang optimal dibandingkan dengan menggunakan metode VAM-MODI pada kasus transportasi tidak seimbang. Kemudian menurut Hidayat (2016) menggunakan metode improved exponential approach pada masalah transportasi tidak seimbang diperoleh biaya pendistribusian pada PT. Prima Jasa Logistik Bulog Cabang Jawa Tengah telah optimal dibandingkan dengan menggunakan metode exponential approach. Kemudian penelitian yang dilakukan Purwanti, dkk (2019) menggunakan metode zero suffix pada masalah transportasi tidak seimbang pada Perum Bulog Divre Kalbar Pontianak juga telah didapatkan biaya distribusi yang optimal.
Berdasarkan penelitian terdahulu, penelitian ini bertujuan untuk mengetahui perbandingan metode improved exponential approach dan zero suffix dalam menentukan solusi optimal pada masalah transportasi yang dialami oleh UD Sinar Jaya Abadi. Perusahaan ini bergerak dalam bidang pendistribusian beras. Namun perusahaan ini belum menggunakan metode khusus untuk mendistribusikan produk berasnya. Oleh karena itu, diperlukan sebuah perencanaan agar rute pendistribusian yang ditempuh dapat optimal sehingga biaya distribusinya juga optimal.
Penelitian ini hanya membahas pendistribusian beras putri sejati 25 kg dari bulan Januari sampai Maret 2021. Dengan memperhitungkan biaya yang dikeluarkan perusahaan dari masing-masing agen ke tempat tujuan. Daerah pendistribusian yaitu Denpasar, Badung, dan Gianyar, dan diasumsikan jalur dapat dilalui oleh kendaraan perusahaan truk (pick-up).
Tempat dan Waktu Penelitian
Tempat pelaksanaan penelitian ini adalah pada salah satu perusahaan pendistribusian beras di daerah Denpasar, yaitu pada UD Sinar Jaya Abadi. Sedangkan waktu yang digunakan
penulis untuk mengumpulkan data dalam penelitian ini adalah dari bulan Januari sampai bulan Maret 2021.
Jenis dan Sumber Data
Data yang digunakan dalam penelitian ini diperoleh dari perusahaan UD Sinar Jaya Abadi. Data yang digunakan merupakan data sekunder. Data-data tersebut berupa data yang diperoleh dari dokumen atau pembukuan pada UD Sinar Jaya Abadi. Adapun data-data yang diperlukan yaitu data persediaan (supply), data permintaan (demand), banyaknya beras putri sejati 25 kg yang didistribusikan dari masing-masing agen ke tempat tujuan dan biaya transportasi dari sumber ke tempat tujuan.
Variabel penelitian
Variabel yang digunakan dalam penelitian ini adalah jumlah persediaan beras putri sejati 25 kg pada masing-masing agen (aij) i=1,2,3, jumlah permintaan beras putri sejati 25 kg pada masing-masing tujuan (bij∙) j=1,2,3,.. .,8, banyaknya beras putri sejati 25 kg yang didistribusikan dari agen i. ke tempat tujuan j kemudian biaya yang dikeluarkan oleh UD Sinar Jaya Abadi dari agen i ke tempat tujuan j (Cij)
Tabel 1. Nama Indeks i dan j
|
i |
Agen |
j |
Tempat Tujuan |
|
1 |
Monang Maning |
1 |
Toko Mekar Sari |
|
2 |
UD. Sinar Wangi | ||
|
2 |
Gatsu Barat |
3 |
Toko Sari Artha |
|
4 |
UD. Mas Ayana | ||
|
5 |
Toko Dharma | ||
|
3 |
Gianyar |
6 |
Toko Subur Jaya |
|
7 |
UD Amertha | ||
|
8 |
Toko Ayu Mega |
Metode Analisis Data
Berikut merupakan langkah-langkah dalam analisis data yaitu :
-
1. Mengumpulkan data berupa data-data
persediaan (supply), data permintaan
(demand), biaya transportasi, dan
banyaknya beras putri sejati 25 kg yang didistribusikan dari masing-masing agen ke tempat tujuan pada bulan Januari sampai Maret 2021 pada UD Sinar Jaya Abadi.
-
2. Membentuk fungsi tujuan dan fungsi kendala
-
3. Menghitung solusi optimal dengan metode improved exponential approach dan zero suffix.
-
4. Interpretasi hasil
Langkah-langkah menghitung solusi optimal dengan improved exponential approach (Hidayat, 2016) :
-
1. Membentuk tabel transportasi dari persoalan transportasi yang telah diberikan
-
2. Membentuk tabel transportasi yang seimbang.
-
3. Mengurangi setiap entri baris i (kolom j') pada tabel transportasi dengan entri minimum baris i (kolom j') masing-masing. Sehingga setiap baris i (kolom j ) pada tabel transportasi setidaknya memiliki satu nilai yang tereduksi menjadi nol.
-
4. a. Memilih biaya yang telah tereduksi menjadi nol pada entri kolom j. Kemudian memeriksa apakah jumlah permintaan pada kolom j sudah kurang dari sama dengan jumlah persediaan pada baris yang bersesuaian dengan biaya yang tereduksi menjadi nol
-
b. Memilih biaya yang telah tereduksi menjadi nol pada entri baris i. Kemudian memeriksa apakah jumlah persediaan pada baris i sudah kurang dari sama dengan jumlah permintaan pada kolom yang bersesuaian dengan biaya yang telah tereduksi menjadi nol.
Apabila langkah 4 telah terpenuhi lanjut ke langkah 6. Apabila belum maka lanjut ke langkah 5.
-
5. Membuat garis horizontal atau vertikal untuk setiap baris i (kolom j') yang memiliki angka nol. Memilih biaya terkecil pada entri yang tidak terkena garis, selanjutnya biaya yang tidak terkena garis dikurangkan dengan biaya terkecil yang telah dipilih. Kemudian menambahkan biaya yang terpilih ke biaya yang terletak di perpotongan dua garis. Kembali ke langkah 4.
-
6. Memilih entri ij yang telah tereduksi menjadi nol. Jika telah terpilih dilanjutkan dengan menetapkan penalti eksponen.
Penalti eksponen adalah jumlah nol
berturut-turut pada masing-masing baris i dan kolom j yang bersesuaian dengan entri ij yang terpilih. Jika entri ij yang terpilih terletak pada entri 11 maka jumlahkan nilai nol yang terletak pada baris 1 dan kolom 1. Kemudian menghitung
jumlah angka nol (tidak termasuk yang dipilih menjadi penalti eksponen) dalam baris dan kolom yang bersesuaian. Mengulangi prosedur untuk semua nol dalam tabel.
-
8. Menandai baris atau kolom yang telah dialokasikan untuk tidak dimasukkan dalam perhitungan selanjutnya. Kemudian kembali ke langkah 3 hingga semua permintaan dan persediaan terpenuhi.
-
9. Langkah terakhir yaitu menghitung biaya yang optimal.
Langkah-langkah menghitung solusi optimal dengan zero suffix (Fegade, 2012):
-
1. Membentuk tabel transportasi dari persoalan transportasi yang telah diberikan
-
2. Membentuk tabel transportasi yang seimbang.
-
3. Mengurangi setiap entri baris i (kolom j') pada tabel transportasi dengan entri minimum baris i (kolom j') masing-masing. Sehingga setiap baris i (kolom j ) pada tabel transportasi setidaknya memiliki satu nilai yang tereduksi menjadi nol.
-
4. Memilih ij yang telah tereduksi menjadi nol kemudian cari nilai suffix value. Suffix value (S) adalah penjumlahan biaya dari sisi yang berdekatan dengan entri ij yang tereduksi menjadi nol yang lebih besar dari nol dibagi jumlah entri ij yang ditambahkan. Apabila biaya terpilih terletak pada entri 11 maka nilai S adalah jumlah biaya pada entri 12 dan 21 dibagi 2, dengan prosedur yang sama cari Suffix Value untuk semua biaya yang telah tereduksi menjadi nol dalam tabel.
-
5. Pilih maksimum dari S, jika memiliki satu nilai maksimum maka terlebih dahulu diberikan pasokan untuk permintaan atau persediaan yang sesuai dengan entri ij dengan nilai S yang paling maksimum. Apabila terdapat nilai yang bernilai sama maka pilih salah satu {aij, blj} dan berikan permintaan atau persediaan semaksimal mungkin dengan memperhatikan persediaan atau permintaan.
-
6. Menandai baris atau kolom yang telah dialokasikan untuk tidak dimasukkan dalam perhitungan selanjutnya. Ulangi 3 hingga langkah 5 sampai semua permintaan terpenuhi.
-
7. Langkah terakhir yaitu menghitung biaya yang optimal.
3. HASIL DAN PEMBAHASAN
Data Penelitian
UD Sinar Jaya Abadi adalah salah satu perusahaan pendistribusian yang berada di daerah Denpasar. Di tengah kondisi Covid-19 yang sedang terjadi perusahaan membatasi jenis beras yang didistribusikan, yaitu beras bermerek putri sejati 25 kg. UD Sinar Jaya Abadi ini memiliki tiga agen yang masing-masing tersebar di daerah Denpasar, Badung, dan Gianyar. Proses pendistribusian beras yang dilakukan oleh UD. Sinar Jaya abadi ini dilakukan menggunakan kendaraan perusahaan berupa truk pick-up.
Tabel 2. Persediaan Masing-masing Agen
Agen
Persediaan (karung)
Monang Maning
4500
Gatsu Barat
3250
Gianyar
3750
Total
11500
Tabel 3. Permintaan Masing-masing Tujuan
Tempat Tujuan
Permintaan (karung)
Jumlah (karung)
Jan
Feb
Mar
Mekar Sari
250
150
200
600
Sinar Wangi
550
450
250
1250
Sari Artha
500
0
0
500
Mas Ayana
670
530
0
1200
Dharma
300
400
55
755
Subur Jaya
400
0
580
980
Amertha
0
615
500
1115
Ayu Mega
0
850
0
850
Total
7250
Tabel 4. Distribusi Beras dari Agen ke Tujuan
i
Agen
j
Tempat Tujuan
Jmlh
1
Monang Maning
1
Toko Mekar Sari
200
2
UD Sinar Wangi
300
3
Toko Sari Artha
150
4
UD Mas Ayana
430
5
Toko Dharma
155
6
Toko Subur Jaya
500
7
UD Amertha
315
8
Toko Ayu Mega
150
2
Gatsu Barat
1
Toko Mekar Sari
250
2
UD Sinar Wangi
400
3
Toko Sari Artha
150
4
UD Mas Ayana
400
5
Toko Dharma
300
6
Toko Subur Jaya
400
7
UD Amertha
250
8
Toko Ayu Mega
150
3
Gianyar
1
Toko Mekar Sari
150
2
UD Sinar Wangi
550
3
Toko Sari Artha
200
4
UD Mas Ayana
370
5
Toko Dharma
300
6
Toko Subur Jaya
80
7
UD Amertha
550
8
Toko Ayu Mega
550
Selanjutnya yaitu skema pendistribusian beras putri sejati 25 kg dari masing-masing agen ke tempat tujuan pada UD. Sinar Jaya Abadi. Adapun skema pendistribusian tersebut dapat dilihat pada Gambar 1.
Monang
Maning
Gatsu Barat
Gianyar
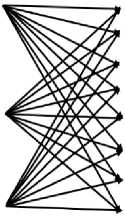
Toko Mekar Sari UD. Sinar Wangi Toko Sari Artha UD. Mas Ayana Toko Dharma Toko Subur Jaya UD Amertha Toko Ayu Mega
Gambar 1. Skema Pendistribusian Beras
Tabel 5. Biaya Rata-rata Distribusi
i
Agen
j
Tempat Tujuan
biaya
1
Monang Maning
1
Toko Mekar Sari
530
2
UD Sinar Wangi
398
3
Toko Sari Artha
300
4
UD Mas Ayana
260
5
Toko Dharma
635
6
Toko Subur Jaya
200
7
UD Amertha
150
8
Toko Ayu Mega
333
2
Gatsu Barat
1
Toko Mekar Sari
800
2
UD Sinar Wangi
214
3
Toko Sari Artha
267
4
UD Mas Ayana
225
5
Toko Dharma
338
6
Toko Subur Jaya
225
7
UD Amertha
192
8
Toko Ayu Mega
300
3
Gianyar
1
Toko Mekar Sari
600
2
UD Sinar Wangi
176
3
Toko Sari Artha
240
4
UD Mas Ayana
322
5
Toko Dharma
405
6
Toko Subur Jaya
500
7
UD Amertha
128
8
Toko Ayu Mega
64
Berdasarkan data pada Tabel 4 dan Tabel 5 diperoleh total biaya pendistribusian beras putri
sejati 25 kg pada UD Sinar Jaya Abadi dari bulan Januari sampai Maret 2021 sebelum optimisasi adalah sebesar Rp 2.075.005,00
Formulasi Model Permasalahan Pendistribusian Beras
Berdasarkan Tabel 2 dan Tabel 3 dapat dilihat bahwa total persediaan dan permintaan beras putri sejati 25 kg berturut-urut dari bulan Januari sampai Maret 2021 adalah sebanyak 11500 dan 7250 karung. Sehingga dapat dikatakan bahwa persoalan transportasi ini belum seimbang karena terdapat kelebihan jumlah persediaan beras putri sejati 25 kg sebanyak 4250 karung. Untuk dapat menyerap kelebihan tersebut dapat ditambahkan kolom/ tujuan dummy dengan asumsi biaya distribusi sebesar 0. Sehingga formulasi model transportasi pada permasalahan pendistribusian beras putri sejati 25 kg yaitu sebagai berikut : z = 530%11 + 398%12 + 300x13 + 260x14
+635x15 + 200x16 + 150x17 + 333x18 + 0x19 + 800x21 + 214x22 + 267x23 +225x24 + 338x25 + 225x26 + 192x27 +300x28 + 0x29 + 600x31 + 176x32 +240x33 + 322x34 + 405x35 + 500x36 +128x37 + 64x38 + 0x39
dengan kendala
x11 + x12 + x13 + x14 + x15 + x16 + x17 + x18 + x19 = 4500
x21 + x22 + x23 + x24 + x25 + x26 + x27 + x28 + x29 = 3250
x31 + x32 + x33 + x34 + x35 + x36 + x37 + x38 + x39 = 3750 x11 + x21 + x31 = 600 x12 + x22 + x32 = 1250 x13 + x23 + x33 = 500 x14 + x24 + x34 = 1200 x15 + x25 + x35 = 755 xi6 + x26 + x36 = 980 x17 + x27 + x37 = 1115
xi8 + x28 + x38 = 850 x19 + x29 + x39 = 4250 xij ≥ 0,i = 1,2,3 dan j = 1,2,3,..., 9
Perhitungan Solusi Optimal
Sebelum dilakukan perhitungan solusi optimal menggunakan metode improved exponential approach dan metode zero suffix, terlebih dahulu dibentuk tabel transportasi. Berdasarkan data yang telah diketahui yaitu beberapa agen dan tempat tujuan dapat dimisalkan MM adalah Agen Monang Maning, GB adalah Agen Gatsu Barat, GI adalah Agen Gianyar, MS adalah Toko Mekar Sari, SW adalah UD. Sinar Wangi, SA adalah Toko Sari Artha, MA adalah UD. Mas Ayana, D adalah Toko Dharma, SJ adalah Toko Subur Jaya, A adalah UD. Amertha, AM adalah Toko Ayu Mega, d adalah Variabel Dummy, Su adalah Persediaan (Supply), De adalah Permintaan (Demand).
Perhitungan Solusi Optimal Improved Exponential Approach Method
-
1. Untuk dapat menyelesaikan persoalan transportasi ini dapat dibuat sebuah matriks m × n dengan entri ij merupakan biaya dari masing-masing agen (i) ke masing-masing tujuan (j). Berdasarkan formulasi model yang telah dibuat diketahui bahwa pada kasus ini terdapat 3 agen dan 9 tujuan sehingga dapat dibuat matriks 3 × 9. Berdasarkan Tabel 4 entri ij merupakan biaya distribusi rata-rata perkarung beras dari masing-masing agen (i) ke masing-masing tujuan (j). Dapat disajikan dalam tabel yang tersusun seperti pada Tabel 6.
-
2. Pada Tabel 6 dapat diketahui bahwa pada persoalan transportasi ini terdapat penambahan kolom dummy. Sehingga lanjut ke langkah 3.
Tabel 6. Tabel Transportasi Awal
|
Agen |
Tujuan |
Su | |||||||||||||||||
|
MS |
SW |
SA |
MA |
D |
SJ |
A |
AM |
d | |||||||||||
|
MM |
530 |
398 |
300 |
260 |
635 |
200 |
150 |
333 |
0 |
4500 | |||||||||
|
GB |
800 |
214 |
267 |
225 |
338 |
225 |
192 |
300 |
0 |
3250 | |||||||||
|
GI |
600 |
176 |
240 |
322 |
405 |
500 |
128 |
64 |
0 |
3750 | |||||||||
|
De |
600 |
1250 |
500 |
1200 |
755 |
980 |
1115 |
850 |
4250 |
11500 | |||||||||
-
3. Kurangi setiap entri baris i. dengan entri minimum kolom masing-masing. Dapat
minimum baris masing-masing. Kemudian dilihat pada Tabel 7.
kurangi setiap entri kolom j dengan entri
Tabel 7. Pengurangan Entri Kolom dan Baris Minimum
|
Agen |
Tujuan |
Su | |||||||||||||||||
|
MS |
SW |
SA |
MA |
D |
SJ |
A |
AM |
d | |||||||||||
|
MM |
0 |
222 |
60 |
35 |
297 |
0 |
21 |
269 |
0 |
4500 | |||||||||
|
GB |
270 |
37 |
27 |
0 |
0 |
25 |
63 |
236 |
0 |
3250 | |||||||||
|
GI |
70 |
0 |
0 |
97 |
67 |
300 |
0 |
0 |
0 |
3750 | |||||||||
|
De |
600 |
1250 |
500 |
1200 |
755 |
980 |
1115 |
850 |
4250 |
11500 | |||||||||
4. Kemudian berdasarkan Tabel 7.
-
a. Memilih biaya yang telah tereduksi menjadi nol pada entri kolom j. Kemudian
memeriksa apakah jumlah permintaan pada kolom j sudah kurang dari sama dengan jumlah persediaan pada baris yang bersesuaian dengan biaya yang tereduksi menjadi nol.
600 < 4500 1250 < 3750 500<3750
1200 < 3250 775 < 3250 980 < 4500
1115 < 3750 850 < 3750
-
b. Memilih biaya yang telah tereduksi menjadi nol pada entri baris i. Kemudian memeriksa apakah jumlah persediaan pada baris i sudah kurang dari sama dengan jumlah permintaan pada kolom yang bersesuaian dengan biaya yang telah tereduksi menjadi nol.
4500 < 600+980+4250
3250 < 1200+755+4250
3750 < 1250+500+1115+850+4250
Karena langkah 4a dan 4b telah terpenuhi yaitu jumlah permintaan (persediaan) pada masing-masing kolom (baris) sudah kurang dari sama dengan jumlah persediaan (permintaan) pada baris (kolom) yang bersesuaian dengan biaya yang telah tereduksi menjadi nol. Lanjut ke langkah 6.
Langkah 6 menentukan penalti eksponennya Kemudian menghitung jumlah angka nol (tidak termasuk yang dipilih)
-
1. baris 1 dan kolom 1 penalti eksponennya 2 jumlah nol (tidak termasuk yang dipilih) 8.
-
2. baris 1 dan kolom 6 penalti eksponennya 2 jumlah nol (tidak termasuk yang dipilih) 8.
-
3. baris 2 dan kolom 4 penalti eksponennya 2 jumlah nol (tidak termasuk yang dipilih) 8.
-
4. baris 2 dan kolom 5 penalti eksponennya 2 jumlah nol (tidak termasuk yang dipilih) 8.
-
5. baris 3 dan kolom 2 penalti eksponennya 4 jumlah nol (tidak termasuk yang dipilih) 6.
-
6. baris 3 dan kolom 3 penalti eksponennya 4 jumlah nol (tidak termasuk yang dipilih) 6.
-
7. baris 3 dan kolom 3 penalti eksponennya 4 jumlah nol (tidak termasuk yang dipilih) 6.
-
8. baris 3 dan kolom 8 penalti eksponennya 4 jumlah nol (tidak termasuk yang dipilih) 6.
Didapatkan nilai penalti eksponen minimum terletak pada entri c11, c16, C24, C25. Karena terdapat lebih dari satu entri Cij dengan nilai penalti eksponen minimum, maka dipilih entri Cij dengan biaya terendah pada tabel awal transportasi. Berdasarkan Tabel 6 biaya terendah terletak pada entri C16. Sehingga alokasikan sebanyak 980 karung beras putri sejati 25 kg dari agen MM ke tujuan SJ (%16). Berdasarkan pengalokasian tersebut tujuan SJ telah terpenuhi permintaannya Sehingga pada tabel berikutnya tujuan SJ sudah tidak masuk perhitungan. Untuk dapat memenuhi seluruh permintaan dapat diulangi langkah 3 sampai 6 hingga seluruh permintaan dan persediaan terpenuhi. Dapat dilihat pada Tabel 8 untuk hasil akhir pengalokasian menggunakan metode improved exponential approach.
Perhitungan Solusi Optimal Zero Suffix
Langkah 1 Membentuk tabel transportasi dari persoalan transportasi yang telah diberikan (Tabel 6. Tabel Transportasi Awal). Karena tabel transportasi telah seimbang maka sesuai langkah-langkah pada metode zero suffix lanjut ke langkah 3. Kurangi setiap entri kolom j dari
minimum kolom masing-masing kemudian kurangi setiap entri baris i dari minimum baris masing-masing (Tabel 7. Pengurangan Entri Kolom dan Baris Minimum).
Langkah 4 dapat dilihat pada Tabel 7 cari nilai suffix value (S) dari semua biaya yang telah tereduksi menjadi nol.
Perhitungannya sebagai berikut :
C11 =---2---= ~ = 246
-
C16= ----3---- = —=114
-
C24 = 3 =T =53
-
c32 = 2 =T- = 54
-
C33 = 2 = T~ = 62
300 + 63
236
C38 = —= 236
363
182
Langkah 5 pilih nilai S yang paling maksimum. Karena terdapat satu nilai S maksimum yang terletak pada entri C11 maka sesuai dengan permintaan dan persediaan dapat dialokasikan sebanyak 600 karung beras putri sejati 25 kg dari agen MM ke tujuan MS (x11).Berdasarkan pengalokasian tersebut tujuan MS telah terpenuhi permintaannya Sehingga pada tabel berikutnya tujuan MS sudah tidak masuk perhitungan. Untuk dapat memenuhi seluruh permintaan dapat diulangi langkah 3 sampai 5 hingga seluruh permintaan dan persediaan terpenuhi. Dapat dilihat pada Tabel 8 untuk hasil akhir pengalokasian menggunakan metode zero suffix.
Tabel 8. Hasil Akhir Perhitungan Metode IEA dan Zero Suffix
|
Agen |
Tujuan |
Su | |||||||||||||||||
|
MS |
SW |
SA |
MA |
D |
SJ |
A |
AM |
d | |||||||||||
|
MM |
530 600 |
398 |
300 |
260 |
635 |
200 980 |
150 |
333 |
29 |
0 0 |
4500 | ||||||||
|
GB |
800 |
214 |
267 |
225 1200 |
338 755 |
225 |
192 |
300 |
12 |
0 5 |
3250 | ||||||||
|
GI |
600 |
176 1250 |
240 500 |
322 |
405 |
500 |
128 1115 |
64 850 |
3 |
0 |
3750 | ||||||||
|
De |
600 |
1250 |
500 |
1200 |
755 |
980 |
1115 |
850 |
4250 |
11500 | |||||||||
Interpretasi Hasil
Dapat dilihat pada Tabel 8 bahwa untuk seluruh baris persediaan dan kolom permintaan telah optimal menggunakan metode improved exponential approach dan metode zero suffix. Dengan demikian diperoleh biaya distribusi optimal beras putri sejati 25 kg dari bulan Januari sampai Maret 2021 sesuai dengan Tabel 8 sebagai berikut :
z = 530x11 + 200x16 + 0%19 + 225%24 +338x25 + 0x29 + 176x32 + 240x33 +128x37 + 64x38 + Ox39
z = 530(600)+ 200(980)+ 0(2920) +225(1200) + 338(755) + 0(1295) +176(1250) + 240(500) + 128(1115) +64(850) + 0(35)
z = Rp 1.575.815,00
Berdasarkan perhitungan yang telah dilakukan diperoleh perbandingan total biaya yang dikeluarkan menggunakan metode improved exponential approach dan metode zero suffix. Adapun perbandingan biaya pendistribusian setelah dilakukan optimisasi dapat dilihat pada Tabel 9.
Tabel 9. Perbandingan Total Biaya Distribusi
|
Metode |
Jumlah Iterasi |
Biaya Pendistribusian |
|
Metode IEA |
8 |
Rp 1.575.815,00 |
|
Metode zero suffix |
8 |
Rp 1.575.815,00 |
Berdasarkan hasil perhitungan yang telah dilakukan, kedua metode tersebut menghasilkan tiga rute pendistribusian yang sama. Jalur pendistribusian pertama yaitu dari
agen Monang Maning ke toko Mekar Sari dan toko Subur Jaya. Jalur pendistribusian kedua dari agen Gatsu Barat ke UD Mas Ayana dan toko Dharma. Jalur ketiga dari agen Gianyar ke UD Sinar Wangi, toko Sari Artha, UD Amertha, dan toko Ayu Mega dengan biaya pendistribusian optimal yaitu sebesar Rp 1.575.815,00. Adapun selisih atau efisiensi total biaya yang dikeluarkan dalam pendistribusian sebelum dan sesudah optimisasi oleh UD Sinar Jaya Abadi sebesar Rp 499.190.00 atau 24%.
4. KESIMPULAN DAN SARAN
Penerapan model transportasi dengan metode langsung yaitu metode Improved Exponential Approach dan metode Zero Suffix diperoleh tiga jalur atau rute pendistribusian yang sama. Jalur pendistribusian pertama yaitu dari agen Monang Maning ke toko Mekar Sari dan toko Subur Jaya. Jalur pendistribusian kedua dari agen Gatsu Barat ke UD Mas Ayana dan toko Dharma. Jalur ketiga dari agen Gianyar ke UD Sinar Wangi, toko Sari Artha, UD Amertha, dan toko Ayu Mega dengan biaya pendistribusian optimal yaitu sebesar Rp 1.575.815,00. Adapun selisih atau efisiensi total biaya yang dikeluarkan dalam pendistribusian sebelum dan sesudah optimisasi oleh UD Sinar Jaya Abadi sebesar Rp 499.190.00 atau 24%.
Adapun saran untuk penelitian selanjutnya terkait pengoptimalan biaya distribusi menggunakan metode transportasi yaitu peneliti dapat membandingkan hasil optimal menggunakan metode improved exponential approach dan metode zero suffix dengan melibatkan faktor kemacetan pada jalur yang akan ditempuh dan juga dapat membandingkan hasil optimal menggunakan metode improved exponential approach atau metode zero suffix dengan metode transportasi lainnya, misalkan seperti metode zero neigbouring atau metode TOCM SUM
DAFTAR PUSTAKA
Badan Pusat Statistik 2017. Analisis Usaha Tani Tanaman Padi Jagung dan Kedelai Tahun 2017. Katalog BPS
Fegade, M. R. 2012. Solving Fuzzy Transportation Problem Using Zero Suffix And Robust Ranking Methodology. IOSR Journal Of Engineering, 02(07), 36–39
Hasan, M. K. 2012. Direct Methods For Finding Optimal Solution Of a Transportation Problem Are Not Always Reliable. International Refereed Journal Of Engineering And Science (IRJES) ISSN (Online), 1(2), 2319–183.
Hidayat, D. A. 2016.. Metode Improved Exponential Approach dalam Menentukan Solusi Optimum pada Masalah Transportasi. Jurnal Matematika (Universitas
Diponegoro), 5(3).251-259
Karundeng, T. N., Mandey, S. L., & Sumarauw, J. S. B. 2018. Analisis Saluran Distribusi Kayu (Studi Kasus Di CV Karya Abadi, Manado). Jurnal EMBA: Jurnal Riset
Ekonomi, Manajemen, Bisnis Dan Akuntansi, 6(3), 1748–1757
Kertiasih, N. K. 2012. Penggunaan Metode Transportasi Dalam Program Linier Untuk Pendistribusian Barang. Jurnal Pendidikan Teknologi Dan Kejuruan, 6(2), 27–35.
Purwanti, L. E., Kiftiah, M., & Fran, F. 2019. Penerapan Metode Zero Suffix dalam Menyelesaikan Masalah Transportasi Fuzzy Dan Linier Studi Kasus : Perum Bulog Divre Kalbar Pontianak. Jurnal Matematika
08(2), 229–238.
Septiana, A. R., Solikhin, & Ratnasari, L. 2017. Metode ASM pada Masalah Transportasi Seimbang. Jurnal Matematika, 20(2), 71– 78.
30
Discussion and feedback