PENERAPAN HUKUM DE MOIVRE PADA PENENTUAN NILAI CADANGAN PREMI ASURANSI JIWA JOINT LIFE

E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 16-22

DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p355

ISSN: 2303-1751

PENERAPAN HUKUM DE MOIVRE PADA PENENTUAN| NILAI CADANGAN PREMI ASURANSI JIWA JOINT LIFE

Rizka Aulia Novalinda^1§, I Nyoman Widana², Ketut Jayanegara³

¹Program Studi Matematika, Fakultas MIPA- Universitas Udayana [Email: [email protected]] ²Program Studi Matematika, Fakultas MIPA- Universitas Udayana [Email: [email protected]] ³Program Studi Matematika, Fakultas MIPA- Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Joint life insurance is| a single policy that| covers two lives. The benefit is paid out when the first person dies. Insurance companies need to calculate and assign premiums and a policy value in order to know. the expected value of the future loss. The study used the quantitative data of mortality for men and women obtained from the Indonesian Mortality Table (TMI) 2011. Data analysis techniques use the New Jersey method of prospects and a legal approach of mortality that is De Moivre’s law. The| purpose| of this study| is to determine| policy value on joint life insurance that applies to De Moivre's laws and compare policy value on joint life insurance that applies De Moivre's laws and without the application of De Moivre's laws. Research shows that joint life insurance policy value with New Jersey methods of prospective and application of De Moivre's law always come into value smaller than those without an application of De Moivre's law, but at the end of period both are worth the same according to the value of their benefits.

Keywords: Joint Life Insurance, Policy Value, New Jersey Method, De Moivre’s Law

• 1.    PENDAHULUAN

Peristiwa kematian seseorang tentu memberikan dampak yang sangat besar terhadap keluarga yang ditinggalkan. Asuransi jiwa sangat diperlukan agar risiko yang akan dihadapi manusia dapat diminimumkan. Futami (1994) menyampaikan bahwa menurut jumlah pihak pemegang polisnya, terdapat dua jenis asuransi| jiwa yakni asuransi| perorangan dan asuransi| kumpulan. Asuransi kumpulan dapat terbagi atas asuransi| joint life serta asuransi| last survivor. Asuransi| joint life sangat memberikan manfaat untuk pelindung keuangan pasangan, bila satu dari pihak tertanggung meninggal semasa jangka waktu kontrak maka pasangan akan mendapatkan biaya pertanggungan.

Perusahaan asuransi diharuskan dapat menghadapi klaim biaya pertanggungan yang kapanpun dapat diajukan oleh pihak pemegang polis. Dana dari himpunan premi yang dibayar pemegang polis akan menjadi pembentuk utama cadangan asuransi. Cadangan diperlukan karena apabila terdapat kerugian aktual dalam pertahun bisa tertutupi oleh cadangan tersebut, tanpa

perlu meningkatkan tarif premi (Hasrullah, 2019).

Terdapat beberapa penelitian terdahulu perihal penentuan cadangan premi, pertama menurut Tewo et al. (2018), nilai cadangan premi asuransi joint life menggunakan metode New Jersey selalu lebih kecil dibandingkan cara prospektif. Menurut Fibrianti (2016), Hukum De Moivre dapat dipergunakan dalam menentukan cadangan premi. Menurut Finan (2011), Hukum De Moivre adalah satu diantara hukum mortalitas pada aktuaria yang diperoleh dari distribusi seragam. Hukum De Moivre dimanfaatkan sebagai penetapan percepatan mortalitas, fungsi kepadatan peluangnya bisa juga digunakan untuk penetapan peluang meninggal serta peluang hidup seseorang.

Dalam artikel ini akan ditentukan cadangan premi pada asuransi| joint life yang menerapkan hukum| De| Moivre serta perbandingan nilai cadangan premi| asuransi| joint life yang menerapkan hukum| De| Moivre dan tanpa penerapan hukum| De| Moivre. Tingkat suku

bunga 3,5% dipergunakan dalam tulisan ini, penentuan cadangan premi asuransi jiwa joint life pada penelitian ini diterapkan metode New Jersey cara prospektif. Penelitian ini memiliki tujuan untuk menentukan cadangan premi pada asuransi| joint life yang menerapkan hukum| De| Moivre serta perbandingan nilai cadangan premi| asuransi| joint life yang menerapkan hukum| De| Moivre dan tanpa penerapan hukum| De| Moivre.

Menurut Bowers et al. (1997), hubungan| antara| fungsi| survival| dengan hukum| De| Moivre adalah:

S(x} =

ω — x

-----= 1

ω

x

ω

sehingga peluang hidup peserta asuransi berdasarkan hukum De Moivre adalah:

n^px =

ω — x — n

ω — x

^px+n =

ω — x — n — 1 ω — x — n

dan peluang meninggal peserta asuransi berdasarkan hukum De Moivre adalah :

n

nPx =

ω — x

β^j = ^pxn∖ +

1

^px+n =

ω — x — n

Menurut Futami (1994), nilai| anuitas hidup akhir| asuransi| joint| life, jangka waktu n| tahun bagi peserta asuransi yang dibayarkan sejumlah 1 rupiah dapat dinotasikan oleh :

n

^axy:n\

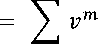
mPxy

m=1

Sedangkan Nilai| dari anuitas| hidup| awal asuransi| joint| life dinotasikan sebagai :

n-1

π    ∖ v^m

^axy:n\          ^u

m=0

m^pxy

Premi tunggal asuransi jiwa dwiguna joint life seumur hidup adalah :

∞

^xy = ∑ »^m+1

m=0

m^xy ^px+m,y+m

Premi tunggal asuransi jiwa dwiguna joint life berjangka n tahun adalah :

^xyrn∖ = ^{1 —} d dχy_rn∖

Premi| tahunan| asuransi| joint| life| dwiguna| dengan jangka waktu n tahun adalah :

_D         ^xy-n\

r —r = ---- ^xy:n|    a -r

^axy:n\

Premi tahunan asuransi jiwa joint life dwiguna seumur hidup untuk masa pembayaran h kali dinotasikan oleh :

_ _Axy_ h^rxy = ^axy*∖

Cadangan premi metode prospektif tahun ke-t bagi asuransi| joint| life| dwiguna, jangka waktu n tahun dan premi dibayarkan pada awal tahun adalah :

t^xy:n\   ^x+ty+t∙.n-t∖   ^Pxy:n\ ^ax+t,y+t:n-t\

Menurut Sembiring (1986), metode| New| Jersey dipergunakan apabila polis memiliki premi| bersih| tahunan| dengan| 20| kali pembayaran| |premi untuk| asuransi| seumur| hidupnya lebih besar dari premi bersih tahunan berjangka, namun premi| kotor lebih besar dari 1,5 —. Cadangan akhir pada tahun pertama

D_x

metode New Jersey adalah nol, maka :

u>=⅛

Bx

P — a J

¹ x:n\ ^{u a}x:19\

• 2.    METODE PENELITIAN

Jenis data kuantitatif yang digunakan dalam penelitian ini adalah data peluang kematian untuk laki-laki dan perempuan yang diperoleh dari Tabel Mortalitas Indonesia (TMI) tahun 2011. Penentuan cadangan premi asuransi jiwa joint life pada penelitian ini, digunakan metode New Jersey dan diterapkan hukum De Moivre. Adapun langkah-langkah penelitiannya yaitu :

• 1.    Penentuan!nilai! anuitas! hidup! berjangka! awal dan akhir !asuransi joint !life menerapkan! hukum! De! Moivre.

• 2.    Penentuan|premi| bersih| tunggal |berjangka asuransi| |joint life menerapkan| |hukum De| Moivre.

• 3.  Penentuan||premi bersih||tahunan berjangka|

asuransi joint| |life menerapkan| |hukum De| |Moivre.

• 4.  Penentuan]]premi bersih]]tunggal asuransi]

joint life] ]seumur hidup] ]menerapkan hukum]]De Moivre] ]kemudian penentuan] premi bersih] ]tahunan asuransi] ]joint life] seumur hidup, pembayaran] ]premi selama] h kali menerapkan] ]hukum De] Moivre.

• 5.    Penentuan] ]premi bersih] ]lanjutan-asuransi] ]joint life] ]menerapkan metode] New Jersey] ]dan hukum] ]De Moivre.

• 6.    Penentuan] ]cadangan premi] ]metode New] ]Jersey dan menerapkan] ]hukum De Moivre.

• 7.  Pengimplementasian] ]pada contoh] ]kasus.

• 8.    Interpretasi hasil.

3. HASIL DAN PEMBAHASAN

Premi bersih tunggal!!!asuransi joint!!life seumur!!hidup dengan!!menerapkan hukum!!De Moivre yaitu : ∞

Axy = ∑ ^t    m^pxy Qx+m,y+m

m=0

= ∑m=0V^m+1 mPxmPy ⁽¹

_—

Px+m_ly+m)

3.1 Penentuan Anuitas Hidup, Premi Tunggal dan Tahunan Berjangka Asuransi Jiwa Joint Life Berdasarkan Hukum De Moivre

∞

= Σ t   ()

m=0

(^1—(

— X —

o — X

m^ ))

^— y

_—

o — y

m)

'ω-x-m-1'

ω-x-m

) (

ω-y-m-1'

ω-y-m

Nilai!!anuitas hidup!!berjangka asuransi joint!!life yang!!menerapkan

akhir! hukum

Premi!!bersih tahunan asuransi!!joint life seumur hidup dengan masa pembayaran premi selama h kali berdasarkan hukum De Moivre yaitu :

De!!Moivre dapat!!dinyatakan oleh : n

^axyn∖

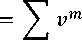
mPxy

m=1

n

= Σ^m(-

m=1

^^p*y = a

^xy

'xy.h∖

Σ∞   ₁-m+1 (^ω'

m=0 ^t    l

∖ I

»-x-i

ω-x

-)(

ω-y-m

ω-y

■) M

'ω-x-m-1'

ω-x-m

) (

'ω-y-m-1'

ω-y-m

^:))

(J)

X -- X

m^ )

— y — m' o—y -

V*-1 „m fω ∑m=0 ^t ( _ι

I~x~ι

ω-x

-K

ω-y-m

ω-y

-)

Nilai!!anuitas hidup!!berjangka awal! asuransi joint!!life yang!!menerapkan hukum De!!Moivre dapat!!dinyatakan oleh:

3.2 Penentuan Premi Lanjutan Asuransi Joint Life Menerapkan Metode New Jersey dan Hukum De Moivre

n-1

Premi bersih lanjutan asuransi joint life berdasarkan hukum De Moivre yaitu :

π         ^m

^xyn∖    ∕ ^t

m=0

m^pxy

j    Cxy

<x^J = ——

Dxy

n-1

= ∑_vm ()

m=0

o

X —

— X

m^ ^o

— y — m' o-y -

Premi bersih tunggal berjangka asuransi jiwa joint life yang menerapkan hukum De

Moivre dapat dinyatakan oleh :

^Axy:n\    ¹ d ^axyn∖

= 1

— d (∑m=1>v^m

(

-x-m

ω-x

)(^-y-y^m))

Premi bersih tahunan berjangka asuransi joint!!life dengan!!!menerapkan hukum!!!De Moivre yaitu :

P   _   xy.n∖

^pxy.n∖ = X __

^axy∙.n∖

1 — d (∑m^-=¹0V^m

Σn-1 m=0

v^m (—

\ <

I~x~ι

ω-x

-K

ω-y-m

ω-y

ⁱ)

= t(1 —

ω-x-1

ω-y-1

ω-x

ω-y

)

β^j = P xyn∖ +

P

^r xy.n∖

— a^]

^axy.19∖

1-a (∑m^-=¹0^^m (-_l

yn-1 .,mi f^ ∑m=0^v ( ,

»-x-m'

ω-x

»-x-m'

ω-x

)(

i(≡)J

+

)

■ ω-y-m'

(1-_a (∑ny=^ιo_v^m p_ω-_x

{    ∑ⁿ                 '

∑m=1t^m ( t(1 —

—

ω-y

• -x-m'

ⁱ ∑ >

' ω-y-m^   f

Oi-y

ω-x-m

ω-x

)(

ω-y-m

ω-y

)

ω-x-1 ω-y-1'

∑m - f (

ω-x

ω-y

)

ω-x-m

ω-x

■)(

ω-y-m

ω-y

■)

3.3 Penentuan Cadangan Premi Metode New Jersey dan Menerapkan Hukum De Moivre

3.4.1 Cadangan Cara Prospektif dengan Metode New Jersey

Cadangan cara!!prospektif metode new jersey asuransi!!joint life berdasarkan hukum De Moivre dapat dinyatakan sebagai:

Pertama!!akan ditentukan!!!nilai anuitas! hidup berjangka awal dengan n = 30 dan n = 20 diperoleh sebagai berikut :

29

t^xy:n|   ^Ax+t,y+t:n-t|

^ax+t,y+t:20-t|

dengan :

—

_—

(^{βj — P}xy:i2|)

^xy:n| ^tx+t,y+^n-t∣

^t45,40^0∣ = Σ

m=0

υ^m mP45,40

(4.13)

^Ax+t,y+t:n-t| = ¹

—

j    n-t-1,,m t^ω-x+^t-m~∖ f^ω-y+^t-my

^m=0     ∖ ω-x+t ∕ ∖ ω-y+t ∕ J

β^j =

1-d (∑^n--¹₀ .m (^-^m)(^-^y-^m))

∣4j^m 0    ∖ _ω-_χ     ω-y Jl

it.

vn-1 „m (ω^-¾^-myω^-y-m ^^m=0   ∖ ω-x √∖ ω-y /

+

(1-d(∑m-=1,>>^mP-g^m

{  ∑m^-=ι^^m(^--m

)(

'.^

'ω-y-m^ f

ω-y

_—

∑m=1V^m (

v (1 —

ω-x-m

ω-x

'.m

ω-x-1 ω-y-1

ω-x ω-y

)

P-T = xy:n|

∑m⁹=1v^m (

ω-x-m

ω-x

)(^ω≡

1 —d (∑m^-=¹0V^m (

• -x-m

ω-x

≡∣^m))

yn-l m f^ω ∑m=0 ^{u (} _ι

• -x-m

ω-x

∖ ∕ω-y-m∖ J ∖ ω-y J

20-t-1

∑_m /ω — x + t — m∖∕ω

^V™ ⁽ ω — x + t )Γ

— y + t — ω — y + t

m^

n-t-1

Σ/ω — x + t — m∖ ∕ω

^{vm (}^—x+τ)r

— y + t — ω — y + t

m^

3.4 Implementasi Pada Contoh Kasus

Diberikan asumsi-asumsi berikut sebagai contoh kasus, umur peserta saat mendaftarkan asuransi adalah (x) 45 tahun dan (y) 40 tahun, untuk produk asuransi berjangka 30 tahun. Nilai santunan (S) adalah Rp.100.000.000,00 serta premi kotor adalah Rp.5.000.000,00 pada tingkat suku bunga 3,5%. Perkiraan usia maksimal untuk peserta yaitu 111 tahun. Langkah pertama adalah menentukan faktor diskon dan tingkat diskon maka :

1

1

^v = (T+o = (TTws) = ⁰,⁹⁶⁶¹⁸

d = 1 — V = 0,03382

= 1 +0,96239 +  + 0,19007

= 16,53034

19

'45,40:20| = Σ ^^m m^p45,40

m=0

= 1 +0,96239 + ••• + 0,40760

= 13,70063

Nilai premi tunggal, premi tahunan dan premi natural asuransi jiwa joint life selama 30 tahun, diperoleh :

A -  —r= 1

45,40:30|    ⁱ

=1

_—

_—

d &45,40:30|

0,03382(16,53034)

= 0,44100

A

_

^r45,40:30| ^t,

^15,0 '⁰    0,02668

'45,40:20|

Nilai premi tunggal asuransi jiwa joint life seumur hidup diperoleh :

∞

^A45,40

Premi

premi

= ∑ ^v    m^p45,40 ^p45+m,40+m

m=0

= (0,00379) + (0,00412) + •••

= 0,40182

tahunan dengan 20 kali pembayaran untuk asuransi joint life seumur hidup

diperoleh :

_n    _  ^A45,40

20^r45,40 = „    ___

^t45,40l20∣

Premi natural substitusikan nilai

0,40182

= 0,02933

13,70063

asuransi joint life dengan p₄₅ = 0,99721 dan p₄₀ =

0,99886 pada tabel mortalita TMI 2011 diperoleh :

[     ^45,40       Z_d

C^j = --— = V (1

^45,40

_—

P45 P40)= 0,00379

1,5 × 7 ‘0

^45,40

Premi kotor

= 1,5 × 0,00379 = 0,00569

pada contoh polis adalah

Rp.5.000.000,00 sehingga dapat disimpulkan bahwa premi kotor lebih besar dari 1,5 × ^C45,40.

D45,40

Berdasarkan hasil perhitungan kedua premi

tahunan dapat disimpulkan bahwa P₄₅₄₀.;] <

₂₀-₄₅₄₀  dan premi kotor > 1,5 × ^C45,40

^{,                                                       β}45,40

sehingga dalam contoh kasus tersebut dapat menggunakan metode New Jersey.

Akan dihitung anuitas akhir asuransi jiwa joint l.fe dengan n = 19 untuk menentukan nilai /^jdiperoleh :

19

^a45,40:19| = Σ ^^m m^45,40

m=1

= 0,96239 + 0,92572+... +0,40760

= 12,29303

Cara yang sama digunakan untuk menghitung cadangan premi pada tahun keenam hingga tahun ke 30.

3.4.2 Cadangan Cara Prospektif dengan Menerapkan Metode New Jersey dan Hukum De Moivre

Nilai tunai anuitas hidup berjangka awal asuransi jiwa joint life selama n = 30 dan n = 20 tahun menggunakan hukum De Moivre:

^a45,40:30| =

29

v^m I-

m=0

111

_-

45

_-

111

_-

45

m) ζ

111

_-

40

_-

111

_-

40

m)

βl   ^-45,4030∣ ⁺

P⅛4O ^r45,⁴⁰:³⁰¹    _β4₅,4₀

= 1 + 0,93814+ - + 0,12228

= 0,02668 +

^a45,40:19|

0,02668 - 0,00379

12,29303

= 13,24609

^a45,40:20| =

19

Σ/

V^m (•

m=0

111

_-

45

_-

111

_-

45

mj (

111

_-

40

_-

111

_-

40

mj

= 0,02854

= 1 + 0,93814 + - +0,27129

Diketahui bahwa dengan menerapkan metode New Jersey, cadangan premi pada akhir tahun pertama adalah nol. Perhitungan cadangan premi menggunakan metode New Jersey berdasarkan metode prospektif pada tahun kedua adalah:

2^45,40:301 = ^47,42:28| ^- (^^j-^-45,40:^)

^47,42:18] ^- ^45,40:30] ^47,42:281

= 0,46783 - (0,02854 - 0,02668)

12,68012 - 0,02668(15,73689)

= 0,02439

= 11,43397

Nilai premi tunggal dan tahunan asuransi jiwa joint life selama 30 tahun menggunakan hukum De Moivre diperoleh:

^45,40:301    ¹   ^ ⁽^"45,40:301)

= 1 - 0,03382 (13,24609)

= 0,55206

‰≡i=f≡=0≡ ^u45,40:30|

Pada tahun ketiga, cadangan preminya adalah : 3^45,40:301 = ^48,43:27] ^{- (/J--}45,40:30]⁾ ^48,43:17] ^{- -}45,40:30| ^48,43:27] = 0,48160 - (0,02854 - 0,02668) 12,15010 - 0,02668(15,32985) = 0,05000

Premi tunggal untuk asuransi joint life seumur hidup menggunakan hukum De Moivre diperoleh : ∞

Σ/ _v^m÷₁ (

m=0

(l-(

111-45 -

111-45

m) (

111 - 40 -

111-40

m)

111-45-m-1'

111-45-m

) (

111-40-m-1'

111-40-m

= (0,02804)+ (0,02669) + -

Pada tahun keempat, cadangan preminya adalah: 4^45,40:301 = ^49,44:26| ^{- (/J--}45,40:30]⁾ ^49,44:161 ^{- -}45,40:30| ®49,44:26| = 0,49557 - (0,02854 - 0,02668) 11,60667 - 0,02668(14,91664) = 0,07601

= 0,51413

Premi tahunan dengan masa pembayaran 20 kali untuk asuransi joint life seumur hidup menggunakan hukum De Moivre diperoleh:

20^-45,40 =

^45,40 ^a45,40:20|

0,51413

11,43397

0,04496

Pada tahun kelima, cadangan preminya adalah : 5^45,40:301 = ^50,45:25] ^{- (/}^^-—45,40:30J⁾ ^50,45:15] ^{- -}45,40:30| ^50,45:25] = 0,50975 - (0,02854 - 0,02668) 11,04919 - 0,02668(14,49725) = 0,10242

Nilai tunai premi bersih lanjutan asuransi jiwa joint life disesuaikan pada tahun pertama menggunakan hukum De Moivre diperoleh:

_aj = ⅛° = 0,02804

^β4S_j40

1,5 × ∣⅛4⁰ = 1,5 × 0,02804 = 0,04206 ¼5,40

Premi kotor pada contoh polis adalah Rp.5.000.000,00 maka premi kotor lebih besar

dari 1,5 ×

^c4⁵-⁴°. Hasil perhitungan kedua premi ^β4S_j40

tahunan

20^45,40

sehingga

menunjukkan dan premi dalam contoh

bahwa  ^P45,40:^ <

kotor > 1,5 × ^c45,4° ^45,4° kasus tersebut dapat

menggunakan metode New Jersey.

Anuitas akhir asuransi jiwa joint life dengan n = 19 menggunakan hukum De Moivre diperoleh : 19

∑_m /111 — 45 — m\ /111 — 40 — m\

^V ( 111 —45 ) (  111 — 40  )

m=1

= 0,93814 + 0,87972 + - + 0,27128

= 10,43397

Nilai β^ yang menerapkan hukum De

Moivre sebagai berikut :

°-49,44:16|   ^P45,40:30| ⁰49,44:26|

= 0,57960 — (0,04298 — 0,04168) 10,08603 — 0,04168(12,43179)

= 0,04829

Pada tahun kelima, cadangan preminya adalah : 5^45,40:30] = ^-50,45:25] ^— (/^^—P45,40:30])

0-50,45:15] ^{— P}45,40:30] °-50,45:25]

= 0,58716 —(0,04298 —0,04168) 9,70303 — 0,04168(12,20808)

= 0,06568

Cara yang sama digunakan untuk menghitung cadangan premi pada tahun keenam hingga tahun ke 30.

Tabel 1. Hasil!!Perhitungan Cadangan!!Premi Asuransi!Jiwa Joint!Life Berdasarkan Hukum De!Moivre dan Tanpa Hukum De Moivre

.                       P.

β^j = ^P45,40:30| +

45,40:30|

—

a^]

045,40:19]

0,04168 — 0,02804

= 0,04168 +---———--

10,43397

= 0,04168 + 0,00130

= 0,04298

Diketahui bahwa dengan menerapkan metode New Jersey, cadangan premi pada akhir tahun pertamanya adalah nol.

Perhitungan cadangan premi asuransi joint life menggunakan metode New Jersey berdasarkan metode prospektif pada tahun kedua dan menerapkan hukum De Moivre diperoleh:

2^45,40:301 = ^47,42:28|   (^{β P}45,40:30|7

0-47,42:181   ^P45,40:30] ^^47,42:28]

= 0,56532 — (0,04298 — 0,04168) 10,79411 — 0,04168(12,85398)

= 0,01549

Pada tahun ketiga, cadangan preminya adalah :

3^45,40:301 = -^48,43:271 ^{— (}/^'^/—P45,40:30])

0-48,43:17] ^{— P}45,40:30] 0-48,43:27]

= 0,57232 — (0,04298 — 0,04168)

10,44924 — 0,04168(12,64691)

= 0,03157

Pada tahun keempat, cadangan preminya adalah:

4^45,40:30] = ^-49,44:26|

_—

C^β^  ^P45,40:30|)

Tah un ke-	Cadangan Premi Tanpa Hukum	Cadangan Premi Dengan Hukum
1	0	0
2	0.024395040387577	0.0154946814869850
3	0.050004600712109	0.0315785181420223
4	0.076014456765895	0.0482926624214619
5	0.102422861076751	0.0656820410653948
6	0.129189929933458	0.0837957644763958
7	0.156266983506554	0.1026875871610912
8	0.183631275997607	0.1224164264773075
9	0.211316843391467	0.1430469480883547
10	0.239364572309215	0.1646502278924980
11	0.267822989392983	0.1873045018111170
12	0.296741857096413	0.2110960167340460
13	0.326160291366459	0.2361199981969124
14	0.356136237147265	0.2624817530789035
15	0.386752867895730	0.2902979288539462
16	0.418100470439856	0.3196979548195837
17	0.450290124670862	0.3508256954097655
18	0.483439007177314	0.3838413513496476
19	0.517669990116459	0.4189236512567573
20	0.553099687839916	0.4562723846157028
21	0.587877307731587	0.4947009627885255
22	0.624024194022844	0.5357566856284288
23	0.661756903042537	0.5797099583217168
24	0.701249178730358	0.6268656571720465
25	0.742863616225482	0.6775683454502794
26	0.786944831516793	0.7322084114508199
27	0.833985071153733	0.7912293171502148
28	0.884539373176961	0.8551361898952551
29	0.939505195430077	0.9245060452512661
30	1	1

n-t-1

^ax+t,y+t:n-t\

Σ V" (^ω

ω

x + t∙

— X + t

m^ ω

— y + t — m' ω — y + t ,

Cadangan Premi Dengan dan Tanpa Hukum De Moivre

1,2

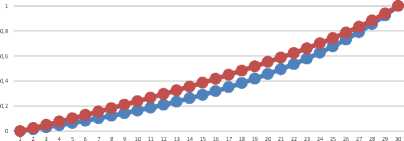
Dengan Hukum        Tanpa Hukum

Gambar 1. Hasil Perhitungan Cadangan!!Premi Asuransi Joint!!Life Dengan dan Tanpa Penerapan Hukum De Moivre

Tabel 1 dan Gambar 1 menunjukkan nilai cadangan premi untuk asuransi jiwa joint life, dapat terlihat bahwa nilai cadangan premi asuransi jiwa joint life yang menerapkan hukum De Moivre menghasilkan nilai lebih kecil dibandingkan nilai cadangan premi!!asuransi joint!!life tanpa menerapkan hukum De!Moivre.

Perhitungan cadangan!!premi asuransi joint!!life 30 tahun dengan!!!metode New!!Jersey dan menerapkan hukum De!!Moivre dari awal!tahun selalu menghasilkan nilai!!!lebih kecil dibandingkan nilai cadangan premi tanpa menerapkan hukum De!!Moivre namun!!pada akhir!!waktu kontrak, keduanya!!bernilai!!sama sesuai dengan jumlah uang pertanggungan.

Disarankan dalam penelitian selanjutnya menerapkan metode lain seperti metode Kanada, metode Zillmer dan metode-metode lainnya serta dapat dikembangkan dengan menggunakan hukum yang lain seperti hukum Weibull, hukum Makeham dan hukum Gompertz.

4. KESIMPULAN DAN SARAN

Berdasarkan pembahasan sebelumnya maka dapat diperoleh cadangan premi yang menerapkan metode New!!Jersey dan!!hukum De!!Moivre pada asuransi joint!!life yaitu :

^^^^^^~

t^v xy:n\

= A

^^^^^^^^^^^^^^™

x+t,y+t:n-t\

_-

(^{βj - P} xytt)

dengan :

^Ax+t,y+t:n-t\

β^j =

^ax+t,y+t:20-t\

= 1

1-a

—

d

(y n-t-1 ∑m=0

(∑m^-=^ι₀v^m (-

∑

> n-1

i m=0

v^m (^-

∖ I

—

^Pxy:n\ ^x+t,y+t:n-t\

V^m (^ω

∖ t

i-x+t-m'

ω-x+t

^; )(^ωω+s^m))

»-x-m'

--x

• -x-m'

—-X

-

-)(

DAFTAR PUSTAKA

Bowers, N. L., Gerber, H. U., Hickman, J. C., Jones, D. A., & Nesbitt, C. J. 1997. Actuarial Mathematics. Schaumburg Illinois: The Society of Actuaries.

Fibrianti, V. L. 2016. Penerapan Hukum De Moivre pada Metode New Jersey dalam Penentuan Nilai Cadangan Asuransi Jiwa Dwiguna.   Skripsi.   FST, Matematika,

Universitas Islam Negeri Maulana Malik Ibrahim, Malang.

Finan, M. B. 2011. A Reading of the Theory of Life Contingency Models: A Preparation for Exam MLC/3L. Arkansas Tech university, Arkansas.

Futami, T. 1994. Matematika Asuransi Jiwa Bagian II. Herliyanto G, penerjemah. Tokyo (JP):  Oriental Life Insurance Cultural

Development Center. Terjemahan dari: Seime Hoken Sugaku Gekan (“92 Revision).

Hasrullah. 2019. Penentuan Cadangan Premi untuk Asuransi Joint Life Dwiguna Murni Berjangka dengan Metode Retrospektif. Skripsi. FST, Matematika, Universitas Islam Negeri Alauddin, Makassar.

Sembiring, R. K. 1986. Buku Materi Pokok Asuransi I Modul 1-5. Jakarta: Karunika.

Tewo, J. L., Widana, I Nyoman, & Oka, T. B. 2018. Penentuan Cadangan Premi dengan Metode New Jersey pada Asuransi Joint Life. E-Jurnal Matematika, 7(3), 226-231.

+

)

■ --y-m'

--y

(1-*(∑m^-Av^m (^m'' {  .    ■ (^-=)f

--x

—-.

x

:)(=))1

■ ω-y-m^   ∣

--y

∑

_—

P = xy :n\

19

m=1

V^m (

V (1

_—

ω-x-m

ω-x

)(

ω-y-m

ω-y

)

ω-x-1 ω-y-1'

ω-x

ω-y

)

∑

19

i m=1

V^m (

ω-x-m

ω-x

)(

ω-y-m

ω-y

)

1

-

d

(V n-1  m ^ω'

∑m=0 ^v (

<-x-m

ω-x

)(≡)

^ax+t,y+t:20-t\ =

y

Z-∣-

^ι n—1

' m=0

20-t-1

V^m (—

∖ I

<-x-m

ω-x

)(

ω-y-m

ω-y

)

∑v(^ω

—

X + t

—

ω

—

X + t

m^ ^ω

—

y + t

—

ω

—

y + t

m^

22