PERAMALAN JUMLAH PENUMPANG PESAWAT BANDARA I GUSTI NGURAH RAI MENGGUNAKAN EXPONENTIAL SMOOTHING DAN RUEY-CHYN TSAUR
on
E-Jurnal Matematika Vol. 10(4), November 2021, pp. 222-228
DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p346
ISSN: 2303-1751
PERAMALAN JUMLAH PENUMPANG PESAWAT
BANDARA I GUSTI NGURAH RAI MENGGUNAKAN EXPONENTIAL SMOOTHING DAN RUEY-CHYN TSAUR
Wildan Fatturahman Mujtaba1§, I Gusti Ayu Made Srinadi2, I Wayan Sumarjaya3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: kwonwildan14@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]
§Corresponding Author
ABSTRACT
Bali province is a tourist destination island with good transportation. Airplane is the most used transportation to go to Bali. Convenience of the airline passengers are the most important thing for I Gusti Ngurah Rai Airport Authorithy. An exact forecast method is needed to predict the numbers of passenger in the future. There are two types of forecasting methods; triple exponential smoothing and Fuzzy Time Series Ruey-Chyn Tsaur, however based on the research Fuzzy Time Series Ruey-Chyn Tsaur is better than triple exponential smoothing due to a small error MAPE (Mean Absolute Percentage Error) of 2,4% and plot is close to actual data.
Keywords: forecasting, air passengers, triple exponential smoothing, Fuzzy Time Series Ruey-Chyn Tsaur
metode peramalan yang diharapkan mampu meramalkan jumlah penumpang pesawat dikemudian waktu atau masa yang akan datang dengan akurasi peramalan yang baik.
Peramalan adalah kegiatan dalam memperkirakan hal yang akan terjadi di waktuyang akan datang dan merupakan teknik dalam hal perencanaan yang efektif dan efisien. Model deret waktu adalah model dengan menggunakan data historis memprediksikan masa depan (Makridaris,1983).
Metode yang digunakan dalam penelitian ini yaitu triple exponential smoothing dan fuzzy time series Ruey-Chyn Tsaur. Metode triple exponential smoothing adalah salah satu metode yang sering digunakan dalam meramalkan data time series untuk plot data trend dan seasonal, kelebihannya ialah kemudahan dalam operasi yang relatif tidak sulit. Pada penelitian terdahulu, metode triple exponential smoothing digunakan untuk meramalkan jumlah penumpang pesawat di Bandara Internasional Adisutjipto memperoleh tingkat akurasi yang baik dengan error MSD yang kecil 82222422 (Munawaroh, 2010)
Metode kedua yang digunakan dalam penelitian ini adalah metode fuzzy time series Ruey-Chyn Tsaur yaitu salah satu metode yang sering digunakan untuk meramal pada fuzzy time series. Salah satu kelebihannya yaitu mempunyai nilaoi MAPE (Mean Absolute Percentage Error) yang kecil dibandingkan metode fuzzy time series lainnya (Jilani,2010). Pada penelitian terdahulu, peramalan penjualan mobil yang dilakukan oleh Berutu pada 2013, menggunakan metode Ruey-Chyn Tsaur ternyata diperoleh nilai MSE (Mean Square Error) yang lebih kecil, dan tingkat ke akuratannya baik yaitu sebesar 87,5%. Berdasarkan penelitian sebelumnya, secara umum metode Ruey-Chyn Tsaur memiliki tingkat akurasi yang cukup baik dibandingkan dengan triple exponential smoothing dengan nilai MAPE yang kecil (Berutu, 2013).
Kedua metode tersebut digunakan mengestimasi dan memprediksi model terbaik pada data penumpang pesawat di Bandar Udara Internasional I Gusti Ngurah Rai.
Data yang digunakan ialah data sekunder merupakan rekap data jumlah penumpang domestik di Bandara Internasional I Gusti Ngurah Rai. Sumber data adalah divisi angkutan udara Kantor Otoritas Bandara Wilayah IV. Data yang digunakan ialah data bulanan dari Januari 2015-Desember 2019.
Penelitian ini menggunakan satu variabel yaitu jumlah penumpang pesawat domestik di Bandara Internasional I Gusti Ngurah Rai. Variabel ini merupakan variabel deret waktu.
Teknik analisis data dilakukan dengan beberapa tahap yaitu:
-
2.3.1. Metode Triple Exponential Smoothing
-
a. Input data.
-
b. Menganalisis efek aditif dan efek multiplikatif data penumpang pesawat.
-
c. Menentukan nilai awal peramalan
-
1. Nilai awal untuk penghalusan total
Lo = 1( Z1 + Z2 + Z3 +∙∙∙ + Zs) s(1)
-
2. Nilai awal untuk penghalusan trend
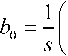
Z -Z Z -Z
Zs+1 Z1 + Zs+2 Z 2 +
ss
-
3. Nilai awal untuk penghalusan seasonal
Sedangkan untuk model Multiplikatif berbeda pada tahap seasonal
L0
-
d. Melakukan pendugaan parameter α untuk penghalusan yang baru dilakukan (level), β untuk unsur trend, serta γ untuk unsur seasonal.
-
e. Menghitung penghalusan model aditif dan multiplikatif dengan persamaan:
-
1. Penghalusan level model Aditif
Lt = α(y, -St-i) + (1 -α)(Lt-1 + bt-1) (5)
-
2. Penghalusan trend model Aditif
bt = β( L, + L,-1) + (1 - β)b,-ι(6)
-
3. Penghalusan seasonal model Aditif
S, = γ(yt - Lt) + (1 - γ)S,-s(7)
-
4. Penghalusan level model Multiplikatif
Lt = α y + (1 - α)(Lt-1 + b-1)(8)
st-1
Multiplikatif
Lt
-
7. Peramalan (TES)
-
f. Menghitung peramalan metode TES model aditif dan multiplikatif.
-
g. Menentukan model terbaik metode TES antar model aditif dan multiplikatif dengan cara membandingkan perhitungan nilai error MAPE.
-
2.3.2. Metode Fuzzy Time Series Ruey-Chyn Tsaur
-
1. Menentukan himpunan semesta
Penentuan himpunan semesta merupakan tahap menentukan nilai maksimum serta nilai minimum untuk setiap data aktual dari jumlah penumpang perbulan untuk sejumlah data penumpang yang akan
dijadikan himpunan semesta
(U=[min,max]).
-
2. Menentukan interval
Pemisahan himpunan semesta ke dalam interval dengan panjang yang sama , dalam menentukan besar interval digunakan metode Strugess.
-
3. Fuzzifikasi data
Fuzzifikasi (penyamaran) dari nilai himpunan nyata menjadi himpunan fuzzy sesuai dengan yang telah dibentuk. Prosesnya didefinisikan jika data real ke-i berada dalam interval U maka hasil
fuzzifikasinya adalah A (1 ≤ i ≤ n).
-
4. Menentukan fuzzy logical relationships Relasifuzzy yaitu Ai → Aj. Dimana Aj merupakan pengamatan pada waktu ke t-1 dan A ialah pengamatan pada waktu ke t
-
5. Menentukan fuzzy logical relationships group
Pengelompokkan nilai FLR yang sama. Hasil dari proses ini juga menjadi dasar perhitungan defuzzifikasi. Sehingga membentuk matriks transisi frekuensi.
-
6. Menghitung hasil ramalan
Mengubah bentuk fuzzy menjadi bilangan real. Pada proses ini bentuk fuzzy juga sekaligus menjadi tahap pemodelan data deret waktu dari metode peramalan ini.
-
7. Menghitung error
Menggunakan MAPE (Mean Absolute Percentage Error) dengan persamaan berikut
MAPE = f ≡%1 n Y-F L n J =1 Y1
(12)
(Tsaur, 2005)
Tabel 3.1 Data Kedatangan Penumpang Pesawat Domestik
|
Bulan |
Tahun | ||||
|
2015 |
2016 |
2017 |
2018 |
2019 | |
|
Jan |
311.636 |
359.951 |
387.804 |
394.330 |
377.073 |
|
Feb |
300.620 |
348.410 |
332.742 |
405.378 |
363.736 |
|
Mar |
309.211 |
390.195 |
375.962 |
437.430 |
369.107 |
|
Apr |
339.866 |
386.318 |
415.931 |
454.709 |
371.883 |
|
Mei |
380.972 |
451.226 |
408.137 |
420.162 |
295.277 |
|
Jun |
358.808 |
383.007 |
403.597 |
481.479 |
457.760 |
|
Jul |
379.299 |
500.963 |
503.684 |
538.578 |
454.068 |
|
Agt |
386.070 |
450.042 |
475.014 |
489.990 |
483.823 |
|
Sep |
346.839 |
412.801 |
440.381 |
468.536 |
418.285 |
|
Okt |
401.273 |
416.044 |
393.517 |
476.692 |
440.904 |
|
Nov |
326.278 |
403.606 |
364.273 |
445.064 |
433.919 |
|
Des |
435.918 |
475.110 |
426.955 |
518.777 |
508.723 |
|
Sumber: Data rekapan angkutan udara Kantor | |||||
Otoritas Bandara Wilayah IV
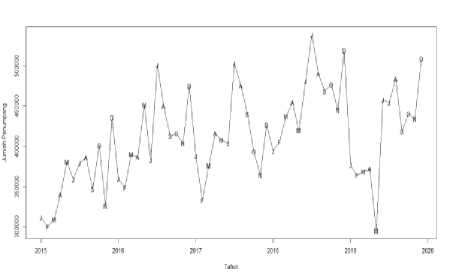
Gambar 3.1. Plot Data Kedatangan Penumpang Pesawat
Dilihat bahwa terjadi kenaikan pada bulan Juli 2018 sebanyak 538.578 penumpang dan penurunan pada bulan Mei 2019 295.277 penumpang. Berdasarkan plot diatas terdapat unsur trend dan seasonal.
Tahap ini data dibagi menjadi data training dimulai dari bulan Januari 2015 sampai bulan Desember 2018. Data testing dimulai dari bulan Januari 2019 sampai bulan Desember 2019. Plot data training dan data testing pada data jumlah penumpang pesawat domestik sebagai berikut:
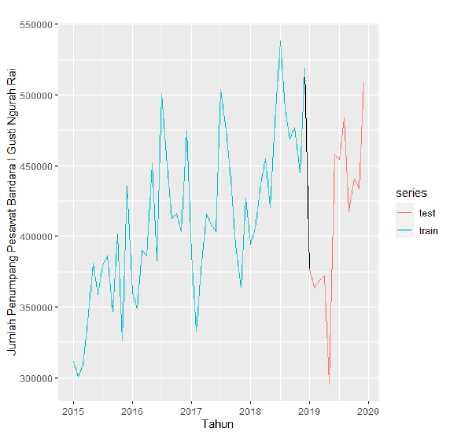
Gambar 3.2. Plot Data Training dan Testing
-
1. Pemilihan parameter α, β dan γ
Menentukan nilai parameter yang akan meminimumkan error. Ketiga parameter tersebut ditentukan dengan bantuan software R.
Tabel 3.2 Nilai Parameter TES Aditif
|
Parameter |
Nilai |
|
α |
0,4196197 |
|
β |
0 |
|
γ |
1 |
Tabel 3.3 Nilai Parameter TES Multiplikatif
|
Parameter |
Nilai |
|
α |
0,4222481 |
|
β |
0 |
|
γ |
1 |
-
2. Peramalan jumlah kedatangan penumpang pesawat domestik
Tahap akhir adalah meramalkan pada dua belas periode pada tahun 2019. Hasil peramalan metode TES aditif dan multiplikatif diperoleh hasil pada tabel 3.4.
Peramalan jumlah penumpang pesawat domestik menggunakan metode TES Aditif pada tahun 2019. Jumlah penumpang tertinggi terjadi bulan Juli 2019 dengan ramalan sebanyak 613.163 penumpang. Penumpang terendah terjadi pada bulan Juli 2019 sebesar 475.194 penumpang. Hasil peramalan metode TES multiplikatif pada tahun 2019 penumpang tertinggi pada Bulan Juli 2019 sebanyak 629.375 penumpang, sedangkan penumpang terendah
terjadi pada bulan Februari 2019 sebesar 464.622 penumpang.
Tabel 3.4 Hasil Peramalan Menggunakan Metode TES Aditif
|
Period |
Peramalan |
|
Jan 2019 |
484.772 |
|
Feb 2019 |
475.194 |
|
Mar 2019 |
504.892 |
|
Apr 2019 |
525.131 |
|
Mei 2019 |
513.216 |
|
Jun 2019 |
554.408 |
|
Jul 2019 |
613.163 |
|
Aug 2019 |
568.934 |
|
Sep 2019 |
541.958 |
|
Okt 2019 |
535.424 |
|
Nov 2019 |
503.825 |
|
Des 2019 |
580.531 |
Tabel 3.5 Hasil Peramalan Menggunakan Metode TES Multiplikatif
|
Period |
Peramalan |
|
Jan 2019 |
484.772 |
|
Feb 2019 |
464.622 |
|
Mar 2019 |
500.121 |
|
Apr 2019 |
525.035 |
|
Mei 2019 |
510.188 |
|
Jun 2019 |
557.202 |
|
Jul 2019 |
629.372 |
|
Aug 2019 |
578.282 |
|
Sep 2019 |
544.606 |
|
Okt 2019 |
533.051 |
|
Nov 2019 |
493.236 |
|
Des 2019 |
581.917 |
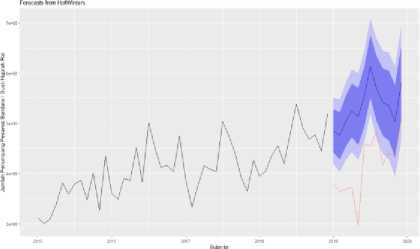
Gambar 3.3. Plot Hasil Peramalan Metode TES Aditif
Fwwasls Iron HoWiMBrs
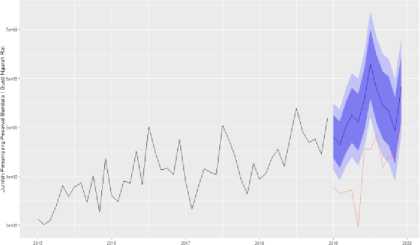
Gambar 3.4. Plot Hasil Peramalan Metode TES Multiplikatif
Berdasarkan nilai error yang diperoleh metode TES Aditif ialah 30,498555, sedangkan pada metode TES multiplikatif ialah 30,308116.
Diperoleh model terbaik yaitu metode TES multiplikatif dengan nilai parameter α = 0,4222481 , β = 0 dan γ = 1
-
3.3 Peramalan dengan metode fuzzy time series Ruey-Chyn Tsaur
Tahapan yang dilakukan pada metode fuzzy time series Ruey-Chyn Tsaur:
-
1. Mencari himpunan semesta dari Januari 2015-Desember 2019 dengan Dmin = 295.277; Dmax = 538.578; D1 = 5.277; D2 =1.422 (U=[290.000; 540.000])
-
2. Pemisahan himpunan semesta ke dalam interval dengan panjang yang sama menggunakan rumus Strugess sebagai berikut:
n = 1 + 3,322log N
= 7
Banyaknya interval yaitu tujuh interval. Langkah berikutnya, yaitu membagi himpunan semesta yang sudah ditentukan, ke dalam 7 interval yang sama panjang untuk nilai linguistiknya dan data terfuzzifikasinya:
{(D , +DΛ-(D - -DS}
n
[(538.578 + 1.422)-(295.277 - 5.277)]
_ [(540.000)-(290.000)J
= 35.714,28 ≈ 35.714
Tujuh interval yang sama dalam himpunan U adalah
u,u ,u ,u ,u ,u ,u
u1 = [290.000,325.714], u2 = [325.714,361.428], U =[361.428,397.142], u4 =[397.142,432.856], u5 =[432.856,468.570], u6 =[468.570,504.284], u7 =[504.284,539.998]
-
3. Berdasarkan himpunan semesta yang sudah diperoleh, dapat ditentukan himpunan semesta untuk setiap data penumpang pesawat domestik, yaitu dengan mengubah data yang berbentuk interval ke dalam bentu linguistik. Data pada bulan Januari 2015 sebesar 311.636 masuk dalam interval u1 =[290.000;325.714] , kemudian dari himpunan semesta terbentuk, ketika berada pada himpunan A maka u memiliki derajat keanggotaan 1.
-
4. Tahap ini menentukan relasi logika fuzzy yaitu A. → A. , dengan A. merupakan
ij i
amatan pada waktu ke t-1 dan A adalah
amatan pada waktu ke t. Dilihat pada data bulan Maret dan April 2015 masing-masing fuzzifikasinya A1 dan A2, maka FLR nya A1 → A2.
-
5. Pengelompokan nilai FLR yang sama. Hasil dari proses ini juga menjadi dasar pada perhitungan defuzzifikasi. Sehingga membentuk matriks transisi frekuensi
’ 2/4
1/4
0
0
1/4
0
0
0
1/7
4/7
1/7
1/7
0
0
1/15
3/15
6/15
3/15
1/15
1/15
0
Pj =
0
1/12
1/12
5/12
2/12
3/12
0
0
1/11
2/11
2/11
2/11
2/11
2/11
0
0
1/7
1/7
3/7
1/7
1/7
_ 0
0
1/3
0
0
1/3
1/3
-
6. Mengubah bentuk fuzzy menjadi bilangan real. Pada tahap ini, proses pengembalian bentuk fuzzy juga sekaligus menjadi tahap pemodelan data deret waktu pada metode ini.
Menghitung hasil ramalan pada Februari 2015 dimana FLRG data aktual 2015 A12(A1),(A2),(A5). Berdasarkan FLRG one to many maka perhitungannya sebagai berikut KL = L t—1) /11 + m 2 P2 + m5P15 ,
dimana Y ialah data aktual sebelum (t-1)
data yang diramalkan yaitu 311.636, P
merupakan nilai probabilitas transisi dari A1 ke A1 yaitu 2/4, m adalah nilai tengah
Tabel 3.5 Perbandingan Hasil Peramalan Dengan Data Aktual
ˆ
Y12 = Y t-1) P1 + m 2 P12 + m5 P5
= 311.636x2/4 + 343.571x1/ 4 + 450.713xl
= 354.389
pada interval A2 yaitu 343.571.
7. Berdasarkan persamaan pada 2.5, maka diperoleh nilai MAPE sebesar 2,4%. Plot data perbandingan antara peramalan dengan data aktual sebanyak 60 data menggunakan bantuan software Microsoft Excel pada Gambar 3.5.
6
45
ω
E ω
o
ω
E B
ω
E
CUD
2015
2016
2017
2018
2019
Aktual
FTS RCT
Gambar 3.5. Perbandingan Plot Peramalan dengan Data Aktual
3.4 Perbandingan hasil peramalan
Solusi untuk mengetahui hasil peramalan yang baik, dilakukan dengan dua cara membandingkan. Pertama, secara analitik
dengan membandingkan nilai error (MAPE). Masing-masing nilai MAPE dari metode triple exponential smoothing dan fuzzy time series Ruey-Chyn Tsaur adalah 0,301 dan 0,024. Kedua secara visual dengan membandingkan plot aktual dengan hasil ramalan dari kedua metode.
Berdasarkan perbandingan peramalan penumpang pesawat di dapatkan hasil bahwa metode fuzzy time series Ruey-Chyn Tsaur lebih baik daripada metode triple exponential smoothing karena nilai MAPE lebih kecil dan plot mendekati data aktual.
|
Periode /4 |
Aktual (orang) |
TES (orang) |
FTS RCT (orang) |
|
Jan-19 |
377.073 |
480.722 |
442.225 |
|
Feb-19 |
363.736 |
464.622 |
385.543 |
|
Mar-19 |
369.107 |
500.121 |
380.208 |
|
Apr-19 |
371.883 |
525.035 |
382.357 |
|
May-19 |
295.277 |
510.188 |
384.153 |
|
Jun-19 |
457.760 |
557.202 |
525.893 |
|
Jul-19 |
454.068 |
629.372 |
555.436 |
|
Aug-19 |
483.823 |
578.282 |
446.090 |
|
Sep-19 |
418.285 |
544.606 |
458.557 |
|
Oct-19 |
440.904 |
533.051 |
431.249 |
|
Nov-19 |
433.919 |
493.236 |
552.370 |
|
Dec-19 |
508.723 |
581.917 |
433.210 |
Berikut plot perbandingannya:
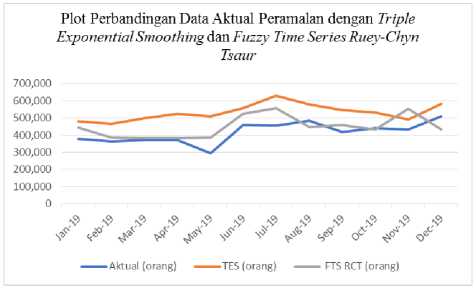
Gambar 3.6. Plot Perbandingan dari Hasil Peramalan dengan Data Aktual
4. SIMPULAN DAN SARAN
Peramalan jumlah kedatangan penumpang pesawat domestik di Bandara I Gusti Ngurah Rai dengan metode fuzzy time series Ruey-Chyn Tsaur lebih baik dari metode triple exponential smoothing dari Brown. Berdasarkan nilai MAPE yang kecil yaitu sebesar 2,4% dan plot yang mendekati data aktual dengan hasil peramalan dari Januari-Desember 2019 secara berurutan; 442.225; 385.543; 380.208; 382.357; 384.153;
525.893; 555.436; 446.090; 458.557; 431.249;
552.370; 433.210.
Pada penelitian selanjutnya diharapkan melakukan analisis dengan metode lainnya dan pada proses analisisnya lebih fokus kepada proses matematisnya bukan pada hasilnya.
DAFTAR PUSTAKA
Badan Pusat Statistik, 2020. Statistik Transportasi Udara Tahun 2019. Jakarta: Badan Pusat Statistik.
Berutu, S. S, 2013. Peramalan Penjualan dengan Metode Fuzzy Time Series Ruey-Chyn Tsaur. Tesis. Pasca Sarjana. Universitas Diponegoro, Semarang.
Jilani A.T, Burney A. M, Ardil C. 2010. Fuzzy Metric Approach for Fuzzy Time Series Forecasting basedon Frequency Density Base Partitioning. International Scholarly and Scientific Research and Innovation: 4(7),1194-1199.
Makridakis, S., Wheelwright, S.C., and McGee, V.E, 1983. Forecasting, methods and Applications. 2nd ed. USA: John Wiley and Sons Inc.
Munawaroh, A.N, 2010. Peramalan Jumlah Penumpang Pada PT. Angkasa Pura I (PERSERO) Kantor Cabang Bandar Udara Internasional Adisutjipto Yogyakarta Dengan Metode Winter’s Exponential Smoothing dan Seasonal ARIMA. Skripsi. Program Studi Matematika. Universitas Negeri Yogyakarta, Yogyakarta.
Tsaur, Yang, Wang, 2005. Fuzzy Relation Analysis in Fuzzy Time Series Model. Computers and Mathematics with Application: 49, 539-548.
228
Discussion and feedback