MODEL DINAMIS AUTOREGRESSIVE DISTRIBUTED LAG (STUDI KASUS: PENGARUH KURS DOLAR AMERIKA DAN INFLASI TERHADAP HARGA SAHAM TAHUN 2014-2018)
on
E-Jurnal Matematika Vol. 9(4), November 2020, pp. 240-250
DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p304
ISSN: 2303-1751
MODEL DINAMIS AUTOREGRESSIVE DISTRIBUTED LAG (STUDI KASUS: PENGARUH KURS DOLAR AMERIKA DAN INFLASI TERHADAP HARGA SAHAM TAHUN 2014-2018)
Mahmudatul Aqibah1§, Ni Luh Putu Suciptawati2, I Wayan Sumarjaya3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mahmudatul94@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
§Corresponding Author
ABSTRACT
The aim of this research is to determine the dynamic model equation of autoregressive distributed lag by using koyck method, to find out the effect of log US dollar exchange rate and log inflation on log stock price in 2014—2018, and to forecast value of log stock price on January 2019—August 2019. The data used in 2014—2018. The data was transformed into logarithm format. Time series plot of log US dollar exchange rate, log inflation, and log stock price suggest that the fluctuation in the data, for instance, both upward and downward trends, during the period. We obtained that the Koyck transformation could changed the lag distribution model into autoregressive distributed lag (ARDL) dynamic model. Furthermore, the log of US dollar exchange rate and log inflation have negative effect on log stock price in particular period. We measured forecasting accuracy using mean absolute prediction error (MAPE) and concluded that ARDL forecasting using Koyck model shows a significant increase in stock price.
Keywords: Autoregressive distributed lag (ARDL), Koyck model, log US dollar exchange rate, log inflation, log stock price.
Analisis regresi merupakan salah satu teknik analisis data dalam statistika untuk menentukan hubungan sebab-akibat antara variabel takbebas (K) dengan satu atau lebih variabel bebas (X). Analisis regresi dengan serangkaian pengamatan terhadap suatu peristiwa diambil dari waktu ke waktu merupakan analisis regresi deret waktu. Analisis regresi deret waktu dilakukan untuk melihat atau meramalkan kondisi pada masa depan (Gujarati, 2006:133).
Model regresi menggunakan data deret waktu tidak hanya menggunakan pengaruh perubahan variabel bebas (X) terhadap variabel takbebas (K) dalam kurun waktu yang sama dan selama periode pengamatan yang sama, namun juga menggunakan periode waktu sebelumnya. Waktu yang diperlukan bagi variabel bebas (X) dalam memengaruhi variabel takbebas (Y) disebut beda kala atau lag (Sarwoko, 2005). Model regresi dengan memasukkan nilai variabel yang menjelaskan
nilai masa kini atau nilai masa lalu dari variabel bebas (X) sebagai tambahan pada model yang memasukkan lag dari variabel takbebas ( ) disebut autoregressive distributed lag (ARDL).
ARDL merupakan gabungan antara metode autoregressive (AR) dan distributed lag (DL). Model AR adalah model regresi yang memuat variabel takbebas dipengaruhi oleh variabel bebas pada waktu t, serta dipengaruhi juga oleh variabel takbebas itu sendiri pada waktu t — 1 (Gujarati, 2006:484). Model distributed lag disebut sebagai model dinamis karena efek perubahan satu unit dalam nilai variabel bebas X terdistribusi pada sejumlah periode waktu (Gujarati, 2006:485). Oleh karena itu, model autoregressive dan model dinamis distributed lag sering disebut satu rangkaian yaitu autoregressive distributed lag (ARDL).
Pada model ARDL terjadi adanya hubungan tidak serentak atau terlambat (lagged relationship) pada variabel bebas (X) dan variabel takbebas (K). Salah satu upaya untuk
mengurangi jumlah faktor keterlambatan dalam model distributed lag maupun masalah multikolinearitas adalah dengan menggunakan model Koyck. Model Koyck merupakan suatu model yang mengasumsikan bahwa koefisien dari variabel yang mengalami keterlambatan dapat menurun secara geometris (Gujarati, 2006:490).
Model ARDL merupakan model dinamis dalam ekonometrika yang bermanfaat dalam ekonometrika empiris karena membuat teori ekonomi yang bersifat statis menjadi dinamis dengan memperhitungkan peranan waktu secara eksplisit. Model ARDL secara umum diterapkan dalam kasus ekonomi.
Salah satu kasus ekonomi adalah pengaruh kurs dan inflasi terhadap harga saham. Dalam konteks perekonomian suatu negara, pertumbuhan nilai mata uang yang stabil menunjukkan bahwa negara tersebut memiliki kondisi ekonomi yang relatif baik atau stabil (Dornbusch, 2008).
Beberapa penelitian yang telah dilakukan mengenai model dinamis autoregressive distributed lag (ARDL), salah satunya adalah Nurahman dkk. (2016) meneliti pengaruh kurs dolar Amerika terhadap produk domestik regional bruto (PDRB) menggunakan model dinamis ARDL. Hasil penelitian tersebut menunjukkan bahwa variabel PDRB atas dasar harga berlaku menurut lapangan usaha pada satu tahun yakni tahun 1993 sampai 2012 dan variabel kurs dolar Amerika pada tahun 1994 sampai 2013 berpengaruh terhadap data PDRB atas dasar harga berlaku menurut lapangan usaha pada tahun 1994 sampai tahun 2013.
Berdasarkan uraian di atas, peneliti tertarik untuk menentukan model dinamis autoregressive distributed lag (ARDL) dengan kasus pengaruh kurs dolar Amerika dan inflasi terhadap saham dengan menggunakan metode Koyck. Penelitian ini bertujuan untuk menentukan persamaan model dinamis ARDL menggunakan metode Koyck, mengetahui pengaruh kurs dolar Amerika dan inflasi terhadap saham dan memperoleh peramalan harga saham pada periode Januari 2019-Agustus 2019.
Regresi Linier Berganda
Regresi linear berganda merupakan pengembangan dari regresi linear sederhana yang menjelaskan hubungan model regresi linear dengan lebih dari satu peubah bebas (Sembiring, 2003). Secara umum model regresi
linear berganda menurut Sembiring (2003):
Yt = + βl%lt + β2^2t+⋯
+ βnXnt + Ut, (1)
-
n=1,2,…․,n
dengan Yt adalah variabel takbebas (dependent variable); ^l , ^2 ,…,Xn adalah variabel bebas (independent variables); βθ adalah
intersep/konstanta; dan βγ , β2,…,βn adalah koefisien regresi; dan Ut merupakan variabel pengganggu (galat) yang bersifat acak.
Asumsi Klasik Model Regresi
Istilah klasik dalam ekonometrika digunakan untuk menunjukkan serangkaian asumsi-asumsi dasar yang dibutuhkan untuk menjaga agar ordinary least square (OLS) dapat menghasilkan estimator terbaik pada model-model regresi. Menurut Gujarati (2006:212) asumsi-asumsi klasik adalah sebagai berikut.
-
1. Model regresi linear dalam parameter, atau
Yt = + βι^i + β2Xj + Ut
-
2. Variabel Xi dan Xj dengan i≠j , tidak berkorelasi dengan faktor galat u.
-
3. Faktor galat u mempunyai nilai tengah sebesar nol, atau E(Ut)=0.
-
4. Homoskedastisitas atau Var (Ui)=σ2 .
-
5. Tidak ada autokorelasi antarfaktor galat Ui dan Uj , atau Cov (Ui, Uj)=0, i≠j.
-
6. Tidak ada kolinearitas antara ^i dan Xj .
Model Autoregressive Distributed Lag (ARDL)
Model Autoregressive (AR)
Autoregressive adalah variabel takbebas dipengaruhi oleh variabel bebas pada waktu t, serta dipengaruhi juga oleh variabel takbebas itu sendiri pada waktu t-1. (Gujarati, 2006:484):
Yt = + β2^t + β3γt + β4γt-l + Ut (2)
dengan Yt adalah variabel takbebas pada saat ke-t pengamatan; Xt , Xt adalah variabel bebas;
-
1 adalah variabel takbebas pada saat ke t-1 pengamatan; βγ , β2 , β3 adalah lereng (kemiringan garis regresi); dan Ut merupakan galat.
Model Distributed Lag (DL)
Model regresi yang memuat variabel takbebas yang dipengaruhi oleh variabel bebas pada waktu t, serta dipengaruhi juga oleh variabel bebas pada waktu t-1,t-2,…․,t-S disebut model distributed lag, sebab pengaruh dari satu atau beberapa variabel bebas
(X) terhadap variabel takbebas (Y) menyebar ke beberapa periode waktu dan bentuk umumnya
dinyatakan (Gujarati, 2004):
Yt = + β0Xt + βl%t + β2Xt-l + β3zt-l + β4xt-2 + β5zt-2 +⋯ + βkXt-k + βk%t-k + Ut ․
Model (3) memperlihatkan
(3) faktor
keterlambatan 1, 2,…․,Xt-n sehingga
variabel takbebas Y dan variabel bebas X
bersifat tidak serentak. Model seperti persamaan (3) disebut model dinamis (model yang melibatkan perubahan dari waktu ke waktu) karena efek perubahan unit dalam nilai variabel bebas X sejumlah n periode waktu.
Terdapat dua jenis model distribusi lag (Gujarati, 2004), yaitu:
-
1. Model Lag Infinite:
Yt = + β0Xt + β4Zt + β2Xt-l + β3zt-l
+ β4Xt-2 + βszt-2 +⋯
+U (4)
Model (4) disebut model lag infinite sebab beda kala tidak diketahui.
-
2. Model Lag Finite:
Yt = + βθX-Lt + β4Zt + β2Xt-l + β3zt-l
+ β4Xt-2 + βszt-2 +⋯ + βkXt-k + βk%t-k + Ut
(5) Model (5) disebut model lag finite dengan beda kala diketahui yaitu sebesar k.
Metode Koyck
Metode Koyck didasari asumsi bahwa semakin jauh jarak lag pada variabel bebas dari periode sekarang maka semakin kecil pengaruh variabel lag terhadap variabel takbebas. Koyck mengusulkan suatu metode pendugaan model lag terdistribusi didasarkan pada asumsi bahwa koefisien β menurun secara eksponensial dari waktu ke waktu (Gujarati, 2004:665) yaitu:
βk = , k=0,1,2,…․dun 0
dengan λ adalah rata-rata tingkat penurunan dari distribusi lag dengan nilai 0<X<1, dan 1-X merupakan kecepatan kesesuaian. Persamaan (6) mempunyai arti bahwa nilai setiap koefisien β lebih kecil dari sebelumnya (0<X<1). Adapun asumsi-asumsi dari aturan Koyck (Gujarati, 2004:666) yaitu:
-
1. Nilai X non-negatif sehingga βk selalu mempunyai tanda yang sama.
-
2. Nilai λ<1 maka bobot βk semakin kecil semakin jauh periodenya.
-
3. Pada metode Koyck, jumlah β adalah penjumlahan jangka panjang (long-run multiplier) yaitu: ∞
∑ βk=1 -Λ+1 -7 (7)
k-0
Berdasarkan asumsi pendekatan Koyck, model distribusi lag jenis infinite lag pada persamaan (4) dengan adanya akibat dari persamaan (6) dapat dituliskan menjadi:
Yt = + β0xt + βl%t + β2XXt-l +β3xzt-l + β4^xt-2 + βsx2zt-2 +⋯+Ut . (8)
Persamaan (8) sulit digunakan untuk memperkirakan koefisien-koefisien yang
banyak dan juga parameter λ yang masuk ke dalam model dalam bentuk tidak linear. Koyck menyarankan untuk mengambil lag satu periode berdasarkan persamaan (8) yaitu:
Yt-I = + β0Xt-1 + β1Zt-1
+β2XXt-2 + β3XZt-2 + β4Z2Xt-3 (9)
+βsx2zt-3+⋯+ut-ι․
Persamaan (9) dikalikan dengan λ sehingga
diperoleh:
XYt-ι = + βθXXt-l + β4ZZt-1
+β2Z2Xt-2 + β3^βzt-2
+β4XiXt-3 + βsZ3Zt-3
+⋯+Xut-ι.
Persamaan (8) dikurangi dengan (10) diperoleh:
Yt - XYt-I = (1-X)+β0xt + β4Zt +(ut - Xut-ι)․
(10)
persamaan
(11)
Secara umum persamaan (11) dapat dituliskan menjadi:
Yt = (1-X)+β0xt + β4Zt + XYt-I + Vt (12) dengan Vt = - Xut-ι .
Prosedur sampai ditemukannya persamaan (12) dikenal dengan nama transformasi Koyck, maka dengan ini hanya perlu mengestimasi parameter a,β0, dan X. Persamaan (12) inilah yang disebut dengan model Koyck. Namun, ada hal yang harus diperhatikan dalam transformasi Koyck yaitu 1 yang diikutsertakan sebagai salah satu variabel bebas sehingga persamaan (12) mengubah model distribusi lag menjadi model autoregresif pada persamaan (2).
Estimasi pada persamaan (12) muncul ^t-1 sehingga disarankan untuk melakukan pemecahan, diperoleh persamaan sebagai berikut:
Yt - XYt-I = (1-X)+β0xt + β4zt + Vt
(13)
atau dapat juga ditulis:
(1-λL ) Yt = (1-A)+β0xt + βι%t
+ γt, (14)
sehingga diperoleh:
=
“(1-h) . + Z
1-A +1- +1-λz,
(15)
model Koyck dengan dua regressor atau fungsi konsumsi jangka panjang (long-run multiplier) pada model Koyck dapat ditulis sebagai berikut:
Yt = + β0 ∑ tiXt-t
∞ ∞
+ βl ∑ KZt-l +∑KVt-l
i=0 i=0
(16)
Median Lag
Model distributed lag (DL) dikarakterisasi oleh median lag dan mean lag. Median lag merupakan nilai lag atau waktu yang menyatakan kondisi besarnya An bernilai setengah (50%) dari total perubahan dalam Y setelah perubahan satu-satuan pada X . Nilai median lag model Koyck dapat dinyatakan
Berdasarkan (19) diperoleh:
ε= - Xβ․ (21)
Oleh karena itu, perkalian matriks galat menjadi:
J= =(Y- Xβ)′(Y- Xβ )
=(Y’ -β′x′)(Y- Xβ )
= - Y'Xβ - β'X'Y + β'X'Xβ
karena ukuran 1×1 maka Y'Xβ=(Y'Xβ)= β'X'Y
= -2β'X'Y + β'X′ Xβ
untuk meminimalkan ε'iεi maka εiεi diturunkan terhadap β sehingga diperoleh persamaan normal:
dj
=0-2X’Y+2X'Xβ =0
2X'Xβ=2X’Y
X'Xβ =
β=(X'X)~1X'Y ․
Sehingga diperoleh estimator untuk OLS yaitu (Gujarati, 2004):
̂=(X'X)~1X,Y․ (22)
sebagai berikut (Gujarati, 2006): log(2) -
logλ
(17)
Mean Lag
Nilai mean lag merupakan nilai lag atau waktu yang diperlukan agar pengaruh (An ) dikatakan signifikan. Nilai mean lag model Koyck dapat dinyatakan sebagai berikut (Gujarati, 2006):
λ
1-λ
(18)
Estimasi Parameter Model
Pada subbab ini dibahas cara mencari nilai duga parameter model autoregressive distributed lag (ARDL) menggunakan ordinary least square (OLS). Estimator dalam metode OLS diperoleh dengan cara meminimalkan
Uji Asumsi Klasik
Uji Normalitas
Uji kenormalan yang dilakukan pada data deret waktu berganda menggunakan metode ARDL adalah uji Lomnicki-Jarque-Bera (LJB). Hipotesisnya adalah sebagai berikut: Hq : residual model menyebar normal, Hy : residual model tidak menyebar normal. Statistik uji Lomnicki-Jarque-Bera (LJB)
adalah:
LJBk = + Bl (23)
dengan Bf atau skewness adalah derajat ketidaksimetrisan suatu distribusi data dan B4 atau kurtosis adalah ukuran ekor suatu distribusi data. Skewness dan dirumuskan sebagai berikut:
τl>1b1
∑ ε12 =∑( * - ⅛
-
βιXii
-
βlXi2
-
-
βkXtp )
(19)
dengan ∑ εi adalah jumlah kuadrat galat (JKG).
Pada notasi matriks jumlah kuadrat galat ∑ εi dapat dituliskan sebagai berikut:
Γειl
kurtosis
(24)
(25)
=
=
ε'iεi=[El ε2 … ]
ε2
βn.
= + ε2 +⋯+ ^n
=∑ ≡12 ․
(20)
dan
_T(b2 -3k)′(b2 -3k)
= 24
dengan
bi =(bu, bl2 , bl3,…,bik)′ dengan J ∑[=1( ̂ kt )3, k=1,2,3,…,K
b2 =(b21, b22, b23,…,b2k)′ dengan
J∑[=1( ̂ ■kt )4, k=1,2,3,…,K
3k=(3,3,3,…,3)′ berukuranK×1.
Statistik LJB secara asimtotis mengikuti distribusi khi-kuadrat dengan derajat bebas 2K. Kriteria uji LJB adalah Hq ditolak apabila LJBk > X2κ;a atau P- value <a (Lütkepohl and Kratzig, 2004).
Uji Heteroskedastisitas
Secara simbolis heteroskedastisitas ditulis sebagai berikut:
E(Ui)=σi . (26)
Pengujian heteroskedastisitas dapat dilakukan, salah satunya dengan uji White. Misalkan dengan model regresi seperti berikut (Gujarati, 2006:405):
Yt = + p2^L + β3γt-l + Ut . (27)
Mengestimasi regresi (27) dengan OLS akan menghasilkan sisaan ei , selanjutnya mengerjakan regresi pelengkap pada regresi (27) sehingga diperoleh e 2= + a2%21 + U3X3t + U4X2i
+ U^Xfl + Uf>X2tX3t + Vi (28) yaitu residu yang diperoleh dari regresi (27) dikuadratkan dan diregresikan pada semua variabel asal, nilai kuadratnya, dan perkalian silangnya. Dapat dilakukan penambahan pemangkatan pada variabel-variabel X asal. Faktor Vi adalah faktor sisaan dalam regresi pelengkap.
Menentukan nilai R2 dari regresi pelengkap (28) dengan hipotesis nol adalah tidak ada heteroskedastisitas artinya semua kemiringan dalam persamaan (28) bernilai nol. Uji White menunjukkan bahwa nilai R2 yang diperoleh dari regresi (28) dikali ukuran sampel (n) mengikuti distribusi X2 dengan derajat bebas sama dengan jumlah variabel penjelas dalam (28) dengan menghilangkan faktor titik potong. Dapat dituliskan sebagai berikut:
n․ R2 ~Xk-I (29)
dengan (k-1) menunjukkan derajat bebas dalam model (28) derajat bebas adalah 5.
Jika nilai khi-kuadrat yang diperoleh dari persamaan (29) melebihi nilai khi-kuadrat kritis pada tingkat signifikansi yang dipilih atau jika nilai P dari nilai khi-kuadrat yang dihitung cukup rendah atau kurang dari 1% atau 5 % maka hipotesis nol ditolak artinya terjadi heterosdekastisitas dan begitu sebaliknya.
Uji Autokorelasi
Autokorelasi adalah adanya hubungan antarresidual pada satu pengamatan dengan
pengamatan lain. Cara yang dapat dilakukan
untuk mendeteksi ada atau tidaknya autokorelasi adalah dengan melakukan uji
Durbin Watson yang didefinisikan sebagai
berikut (Gujarati, 2004):
∑ t= 2 (^ - et-ι) 2_ ∑"=1 et
=
(30)
Mekanisme uji Durbin Watson adalah
melakukan regresi OLS dan mendapat nilai residualnya, selanjutnya yaitu menghitung nilai d-Durbin Watson dan mendapat nilai kritis dL dan du. Hipotesisnya adalah sebagai berikut: Apabila hipotesis nol adalah tidak ada serial korelasi positif, maka:
d< dL = tolak Hq ,d< du = terima Hq .
Apabila hipotesis nol adalah tidak ada serial korelasi baik negatif, maka:
d >4-dL = tolak Hq ,d <4-dL = terima H0 .
Apabila H0 adalah dua ujung, yaitu tidak ada serial korelasi baik positif maupun negatif, maka:
d< dL = tolak Hq ,d>4-dL = tolak Hq , du <d<4-du = terima Hq ․
Peramalan
Pada Peramalan data, ukuran-ukuran ketepatan yang sering digunakan untuk mengetahui ketepatan suatu metode peramalan dalam memodelkan data deret waktu, yaitu nilai MAPE (Mean Absolute Percentage Error), MSD (MeanN Squared Deviation), MAD (Mean Absolute Deviation) MAPE merupakan ukuran ketepatan relatif yang digunakan untuk mengetahui persentase
penyimpangan hasil peramalan, persamaan sebagai berikut:
MAPE=1∑|PE1 |
dengan
Galat persentase (percentage error):
(xt - Ft∖
PEt=( ~1~) ×100%
(31)
(32)
Data yang digunakan dalam penelitian ini berupa data sekunder yang diperoleh dari laman web resmi investing yaitu www.investing.com dan Bank Indonesia yaitu www.bi.go.id. Penelitian ini menggunakan data deret waktu harga saham PT. Telekomunikasi Indonesia. Tbk., kurs dolar Amerika, dan inflasi periode Januari 2014 sampai Desember 2018 dengan rentang waktu per bulan/bulanan.
Pada penelitian ini, Variabel yang digunakan adalah Variabel terikat (Y) yaitu data saham PT. Telekomunikasi Indonesia, Tbk. periode Januari 2014–Desember 2018, variabel bebas ( ¾ ) yaitu data kurs dolar Amerika dan ( ^2) yaitu inflasi pada periode Januari 2014– Desember 2018.
Adapun langkah-langkah dalam penelitian ini adalah :
-
1. Mengumpulkan data saham, kurs dolar Amerika dan inflasi pada periode Januari 2014-Desember 2018 di laman web resmi www.investing.com dan Bank Indonesia yaitu www.bi.go.id.
-
2. Mentransformasi data saham, kurs dolar Amerika dan inflasi kedalam bentuk
logaritma.
-
3. Menguji kestasioneran data yang telah
ditransformasi kedalam logaritma
menggunakan uji Augmented Dickey-Fuller Tes (ADF).
-
4. Melakukan analisis deskriptif terhadap data untuk mengetahui gambaran umum mengenai data log harga saham, log kurs dolar Amerika, dan log inflasi.
-
5. Membuat/mengestimasi persamaan regresi Koyck.
-
6. Melakukan uji statistik F dan uji t pada regresi Koyck.
-
7. Melakukan pengujian asumsi klasik model Koyck pada data residual sebagai berikut:
-
a. Pengujian kenormalan pada residual data dengan statistik uji yang digunakan adalah uji Lomnicki-Jarque-Bera (LJB).
-
b. Pengujian heteroskedastisitas dengan menggunakan statistik uji yang digunakan adalah uji White.
-
c. Pengujian autokorelasi dengan
menggunakan statistik uji yang digunakan adalah d Durbin-Watson.
-
8. Menentukan model dinamis autoregressive distributed lag Koyck.
Analisis Deskriptif
Analisis deskriptif digunakan untuk memberikan gambaran umum mengenai data, yang dilakukan dengan membentuk plot data berupa data harga saham PT. Telekomunikasi Indonesia, Tbk., kurs dolar Amerika menggunakan kurs tengah Rp/U$$ yang dihitung berdasarkan kurs jual dan kurs beli pada setiap akhir bulan, dan inflasi indeks harga konsumen (IHK) pada periode Januari 2014 sampai Desember 2018. Data yang diolah merupakan data yang telah ditransformasi kedalam logaritma.
Tabel 1. Analisis deskriptif data transformasi logaritma periode Januari 2014-Desember 2018
|
No . |
Statistika deskriptif |
Harga saham (Y) |
Kurs dolar Amerika (^1 ) |
Inflasi (¾) |
|
1. |
Jumlah |
60 |
60 |
60 |
|
2. |
Minimum |
3,345 |
4,057 |
0,445 |
|
3. |
Maksimum |
3,671 |
4,181 |
0,922 |
|
4. |
Mean |
3,529 |
4,120 |
0,643 |
|
5. |
Median |
3.560 |
15.178,8 |
8,36 |
Sumber: www.investing.com (2018); www.bi.go.id (2018).
Tabel 1 merupakan tabel analisis deskriptif data transformasi logaritma periode Januari 2014-Desember 2018. Pada data log harga saham PT. Telekomunikasi Indonesia, Tbk., nilai minimum terjadi pada bulan Maret 2014 dan nilai maksimum terjadi pada bulan Juli-Agustus 2017. Data log kurs dolar Amerika, nilai minimum terjadi pada bulan Maret 2014 dan nilai maksimum terjadi pada bulan Oktober 2018. Data log inflasi, nilai minimum terjadi pada bulan Desember 2014 dan nilai maksimum terjadi pada bulan Agustus 2016. Berikut ini diperoleh plot dari data transformasi logaritma, dapat dilihat pada Gambar (1), Gambar (2), dan Gambar (3).
HARGA SAHAM PT. TELEKOMUNIKASI INDONESIA, Tbk.
5000
4500
4000
3500
3000
2500
2000
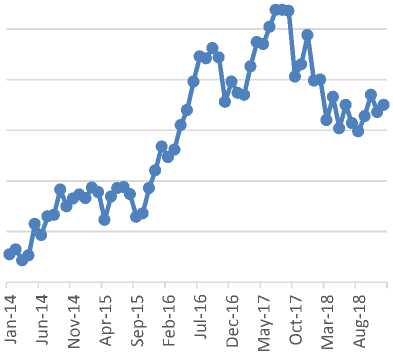
Gambar 1. Plot data log harga saham PT.
Telekomunikasi Indonesia. Tbk. periode Januari 2014-Desember 2018
KURS DOLAR AMERIKA
15500
15000
14500
14000
13500
13000
12500
12000
11500
11000
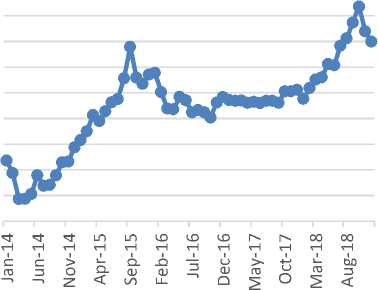
Gambar 2. Plot data log kurs dolar Amerika periode Januari 2014-Desember 2018
INFLASI (%)
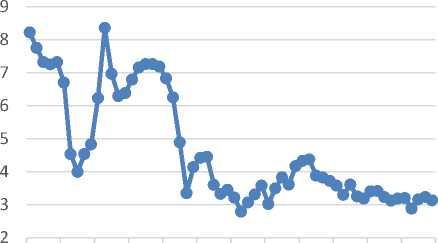
Gambar 3. Plot data log inflasi periode Januari 2014-Desember 2018
Gambar 1. merupakan plot data Yt atau data log harga saham PT. Telekomunikasi Indonesia, Tbk., dapat dilihat bahwa data tidak stasioner. Terjadi tren naik secara kontinu pada periode Januari 2014-Oktober 2016 dan periode Maret 2018-Desember 2018. Data mengalami tren turun pada periode November 2016-Februari 2017.
Gambar 2. memperlihatkan plot data Xt atau data log kurs dolar Amerika, dapat dilihat bahwa data tidak stasioner. Terjadi tren naik pada periode Maret 2014-September 2015 dan periode Oktober 2017-Desember 2018 mengalami peningkatan secara konstan. Terjadi tren turun pada periode Oktober 2015-Januari 2016. Pada bulan Februari 2016-September 2017 nilai kurs mengalami harga yang cukup stabil.
Gambar 3. menunjukkan plot data ^t atau data log inflasi, dapat dilihat bahwa data tidak
stasioner. Terjadi tren turun pada periode Januari-Agustus 2014 dan tren naik pada periode September 2014-Agustus 2014. Pada grafik periode September 2014-Desember 2015 data terlihat mengalami tren naik dan tren turun. Pada periode Januari 2016-Desember 2018 data mengalami nilai yang cukup stabil.
Stasioneritas Data
Tabel 2. Uji akar unit data transformasi logaritma Periode Januari 2014-Desember 2018
|
Variabel |
Level (0) |
Differencing pertama (1) | ||
|
Statistik uji ADF |
P-Value |
Statistik uji ADF |
P- Value | |
|
-1,88549 |
0,336 |
-8,9193 |
0 | |
|
Xt |
-0,88948 |
0,7849 |
-6,5117 |
0 |
|
-1,8852 |
0,336 |
-6,0586 |
0 | |
Berdasarkan Tabel 2. hasil pemeriksaan stasioneritas dari ketiga variabel (Yt , Xt , dan Xt ) diperoleh bahwa kondisi level I(0) ketiga variabel (Yt , Xt , dan Xt) belum stasioner. Semua variabel telah stasioner pada kondisi differencing pertama I(1), sehingga hasil ini mengindikasikan bahwa model Autoregressive Distributed Lag (ARDL) dapat dibentuk dari variabel-variabel tersebut.
Mengestimasi Persamaan Regresi Koyck
Data yang digunakan dalam mengestimasi model Koyck adalah data setelah dimasukkan beda kala (lag) untuk Yt yaitu log harga saham PT. Telekomunikasi Indonesia, Tbk. dan setelah dimasukkan lag Yt-I serta log kurs dolar Amerika ( Xt ) dan log inflasi ( Xt). Hipotesis yang diuji adalah:
Hq : parameter ^l , ^2 tidak berpengaruh signifikan terhadap variabel Yt ,
H^ : parameter βl , β2 berpengaruh signifikan terhadap variabel Yt ․
Hasil estimasi parameter pada model Koyck adalah sebagai berikut:
Tabel 3. Nilai koefisien parameter model Koyck
|
Parameter |
Koefisien |
P-Valu e |
Taraf signifika nsi (a) |
Keputusan |
|
a(1-λ) |
0,799482 |
0,1641 |
> 0,05 |
Menerima H0 |
|
Λ |
-0,047701 |
0,7332 |
> 0,05 |
Menerima H0 |
|
β2 |
-0,080410 |
0,0276 |
< 0,05 |
Menolak H0 |
|
λ |
0,844741 |
0,0000 |
< 0,05 |
Menolak H0 |
Penarikan keputusan menggunakan tingkat signifikansi 5% dan dalam pengolahan data menggunakan ARDL diperoleh output nilai koefisien determinasi (R2) sebesar 0,92 artinya besarnya pengaruh variabel log kurs dolar Amerika dan log inflasi terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. pada tahun 2014-2018 sebesar 92% maka model regresi sudah baik, sehingga diperoleh model sebagai berikut:
Yt = 0,799482 - 0,047701Xt
-0,080410Zt + 0,844741Yt-I (33)
Interpretasi dari model (33) adalah nilai 0,799482 berarti log harga saham PT. Telekomunikasi Indonesia, Tbk. pada periode waktu t memiliki nilai 0,799482 saat tidak ada pengaruh variabel bebas ataupun pengaruh waktu sebelumnya. Setiap penurunan log kurs dolar Amerika sebesar satu satuan akan menyebabkan log harga saham PT. Telekomunikasi Indonesia, Tbk. menurun sebesar 0,047701 satuan dan setiap penurunan log inflasi sebesar satu-satuan akan menyebabkan log harga saham PT. Telekomunikasi Indonesia, Tbk. menurun sebesar 0,080410 satuan. Nilai 0,844741 berarti jumlah nilai log harga saham PT. Telekomunikasi Indonesia, Tbk. periode ke-t dipengaruhi oleh nilai log harga saham PT. Telekomunikasi Indonesia, Tbk. pada periode sebelumnya yaitu sebesar 0,844741 kali lipat dari sebelumnya.
Pengujian Signifikansi Parameter Pada Regresi Koyck
Pengujian signifikansi parameter pada regresi Koyck diperoleh dari pengujian secara simultan. Hipotesisnya adalah sebagai berikut: Hq : variabel X tidak berpengaruh signifikan
terhadap variabel Y,
Hy : variabel X berpengaruh signifikan terhadap variabel Y․
Adapun hasil pengujian secara simultan diperoleh p-value sebesar 0. Penarikan keputusan menggunakan tingkat signifikansi 5%. P-value sebesar 0 lebih kecil dari 5%, sehingga diperoleh kesimpulan menolak Hq . Hal ini berarti model Koyck sudah tepat digunakan, sehingga dapat dilakukan pemeriksaan pengujian secara parsial.
Model Dinamis Autoregressive Distributed lag (ARDL) Koyck
Pemodelan Distribusi Lag (DL)
Pemodelan distribusi lag dilakukan setelah diperoleh model Koyck atau bisa disebut juga dengan model autoregressive pada persamaan (33). Model autoregresif dapat diubah menjadi model distribusi lag untuk jenis infinite lag. Berdasarkan persamaan (33) untuk bentuk model Koyck telah diketahui bahwa nilai estimasi dari parameter A sebesar 0,844741, nilai estimasi dari parameter βy sebesar -0,047701 dan parameter β2 sebesar -0,080410 dan nilai dari parameter
a(1-A) sebesar 0,799482 sehingga untuk nilai estimasi parameter a sebesar 5,149344, diperoleh nilai masing-masing beta dihitung dengan menggunakan persamaan (6) adalah sebagai berikut:
Pl = -0,047701,
Pll = -0,047701 × 0,844741
= -0,0402949904,
P12 = -0,047701 × (0,844741)2
= -0,0340388305,
P13 = -0,047701 × (0,844741)3
= -0,0287539957,
P2 = -0,080410,
P2I = -0,080410 × 0,844741
= -0,0679256238,
P22 = -0,080410 × (0,844741)2
= -0,0573795594,
P22 = -0,080410 × (0,844741)3
= -0,0484708664,
Koefisien βy dan β2 disebut sebagai short-run
multiplier. Penjumlahan parsial nilai-nilai β disebut dengan intermediate-run multiplier. Selanjutnya yaitu menghitung nilai long-run
multiplier, dengan nilai =
-0,047701 diperoleh:
∞
∑1 -0,047701
Pk=(1-A)= 1-A
k-o
= -0,30723501
-0,047701
0,155259
dan nilai β2 = -0,080410 diperoleh:
∑ Pk=(1-1 Λ)= k-o
-0,080410 -0,080410
1-A = 0,155259
-0,51790878
sehingga fungsi konsumsi jangka panjang
(long-run multiplier) pada model Koyck dapat
ditulis sebagai berikut:
Yt = 5,149344 - 0,30723501Xt
-0,51790878Zt .
(34)
Interpretasi dari model (34) adalah nilai 5,149344 berarti log harga saham PT. Telekomunikasi Indonesia, Tbk. pada periode ke- t memiliki nilai 5,149344 saat tidak ada pengaruh variabel bebas. Setiap penurunan log kurs dolar Amerika sebesar satu satuan akan menyebabkan penurunan terhadap harga saham PT. Telekomunikasi Indonesia, Tbk. sebesar 0,30723501 satuan dan setiap penurunan log inflasi sebesar satu satuan akan menyebabkan penurunan terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. sebesar 0,51790878 satuan.
Berdasarkan persamaan model (34) di atas, hasil kesimpulan pengujian secara parsial model dinamis autoregressive distributed lag (ARDL) Koyck diperoleh sebagai berikut:
-
1. Variabel log kurs dolar Amerika tidak berpengaruh terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. pada tahun 2014-2018.
-
2. Variabel log inflasi tidak berpengaruh terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. pada tahun 2014-2018.
-
3. Variabel log harga saham PT. Telekomunikasi Indonesia, Tbk. pada tahun 2014-2017 berpengaruh terhadap log kurs dolar Amerika dan log inflasi pada tahun 2015-2018.
Median Lag
Median lag merupakan nilai lag atau waktu yang menyatakan kondisi besarnya λn
bernilai setengah (50%). Berikut ini diperoleh
nilai median lag sebagai berikut:
log(2) logλ
0,301029995 log(0,844741)
= 4,1081422․
Diperoleh nilai λ = 0,844741 sehingga nilai median lag sebesar 4,1081422. Total dari perubahan variabel takbebas (Y) dibutuhkan lebih dari 4 periode untuk mencapai 50 persen atau pengaruhnya akan bernilai 50 % pada lag ke-4,1081422.
Mean Lag
Nilai mean lag merupakan nilai lag atau waktu yang diperlukan agar pengaruh (λn) bisa dikatakan signifikan. Berikut ini diperoleh nilai mean lag sebagai berikut:
λ 0,844741 0,844741
1-λ=1-0,844741 = 0,155259
= 5,44085045․
Diperoleh nilai λ = 0,844741 sehingga nilai
mean lag sebesar Nilai 5,44085045 berarti pengaruh (λn) dikatakan signifikan setelah lag ke-5,44085045.
Pengujian Asumsi Klasik
Uji Kenormalan Residual
Uji kenormalan residual estimasi pada model ARDL pada persamaan (4)
menggunakan uji Lomnicki-Jarque-Bera (LJB) dengan hipotesis yang diuji adalah Hq : residual model menyebar normal, H^ : residual model tidak menyebar normal.
Perhitungan mencari nilai statistik uji skewness (si), kurtosis (,^4), dan LJBk dibantu dengan menggunakan software Eviews 10. Pada perhitungan software Eviews 10 diperoleh p-value sebesar 0,157962. Penarikan keputusan menggunakan tingkat signifikansi 5%, p-value sebesar 0,157962 lebih besar dari 5%, maka terima Hq . Hal ini berarti, residual estimasi model ARDL pada persamaan (34) menyebar normal.
Uji Heteroskedastisitas
Uji heteroskedastisitas pada model ARDL pada persamaan (34) menggunakan uji White dengan hipotesis yang diuji adalah:
Hq : tidak terjadi heteroskedstisitas,
H^ : terjadi heteroskedatisitas.
Statistik uji yang digunakan adalah jika nilai khi-kuadrat yang diperoleh dari persamaan (29) melebihi nilai khi-kuadrat kritis pada tingkat signifikansi yang dipilih atau jika nilai P- value dari nilai khi-kuadrat yang dihitung lebih kecil dari 1% atau 5% maka tolak Hq , artinya terjadi heterosdekastisitas dan begitu sebaliknya.
Uji White dihitung dengan menggunakan bantuan software Eviews 10. Diperoleh P-value White sebesar 0,2329. Penarikan keputusan menggunakan tingkat signifikansi 5%, dengan demikian P-value sebesar 0,2329 lebih besar dari 5%, maka terima Hq . Hal ini berarti, residual estimasi model ARDL pada persamaan (34) tidak terjadi masalah heteroskedastisitas.
Uji Autokorelasi
Uji autokorelasi model ARDL pada persamaan (34) menggunakan uji d Durbin Watson. Data yang digunakan untuk memperoleh model ARDL pada persamaan (34) berjumlah 60 data yaitu dari bulan Januai
2014 sampai Desember 2018 dengan orde optimum yang dipilih adalah satu. Hal ini berarti beda kala (lag) autokorelasi
antarresidual terbesar yang dapat terbentuk adalah 59. Oleh karena itu, hipotesis yang diuji adalah sebagai berikut:
Hq : tidak terdapat autokorelasi antarresidual model dari lag 1 sampai lag 59,
Hy : terdapat paling sedikit satu autokorelasi antarresidual model dari lag 1 sampai lag 59.
Statistik uji yang digunakan adalah d. Berdasarkan persamaan (34) dihitung dengan bantuan software Eviews 10. Diperoleh nilai d Durbin Watson adalah sebesar 2,258693 sehingga diperoleh letak antara dy <d<(4-du) atau dengan nilai 1,6889 < 2,258693 < 2,3111 oleh karena itu, dapat diambil kesimpulan menerima Hq, artinya tidak terjadi masalah autokorelasi dalam model regresi.
Peramalan Dengan Model ARDL
Peramalan log harga saham PT. Telekomunikasi Indonesia, Tbk. periode Januari 2019 sampai Agustus 2019, terlihat mengalami fluktuatif pada data. Terjadi tren naik pada bulan Januari-Maret 2019 dan terlihat mengalami tren turun pada bulan April-Agustus 2019. Pada bulan Mei-Agustus 2019 terlihat mengalami fluktuatif.
Ukuran Ketepatan Nilai Peramalan
Ukuran ketepatan nilai peramalan menggunakan nilai MAPE. Nilai MAPE pada peramalan harga saham PT. Telekomunikasi Indonesia. Tbk. periode Januari 2019-Agustus 2019 dengan metode Koyck adalah sebesar 3,349%. Nilai MAPE sebesar 3,349 merupakan nilai yang minimum sehingga metode peramalan dengan model Koyck dianggap sebagai metode yang baik digunakan untuk peramalan.
Kesimpulan
Berdasarkan hasil analisis dan pembahasan yang dilakukan maka diperoleh kesimpulan sebagai berikut:
-
1. Bentuk model Autoregressive Distributed Lag Koyck adalah sebagai berikut:
Yt = 5,149344 - 0,30723501Xt
- 0,51790878Zt
Interpretasi dari model di atas adalah nilai 5,149344 berarti log harga saham PT. Telekomunikasi Indonesia, Tbk. pada periode ke-t memiliki nilai 5,149344 saat tidak ada pengaruh variabel bebas. Setiap penurunan log kurs dolar Amerika sebesar satu satuan akan menyebabkan penurunan terhadap harga saham PT. Telekomunikasi Indonesia, Tbk. sebesar 0,30723501 satuan dan setiap penurunan log inflasi sebesar satu satuan akan menyebabkan penurunan terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. sebesar 0,51790878 satu satuan.
-
2. Variabel log kurs dolar Amerika dan log inflasi berpengaruh negatif terhadap log harga saham PT. Telekomunikasi Indonesia, Tbk. pada tahun 2014-2018.
-
3. Hasil peramalan log harga saham PT. Telekomunikasi Indonesia, Tbk. pada periode Januari sampai Agustus 2019 adalah terlihat mengalami fluktuatif pada data. Terjadi tren naik pada bulan Januari-Maret dan terlihat mengalami tren turun pada bulan April-Agustus. Pada bulan Mei-Agustus terlihat mengalami fluktuatif.
Saran
Penelitian ini menghasilkan model peramalan yang cukup akurat untuk variabel harga saham PT. Telekomunikasi Indonesia. Tbk., kurs dolar Amerika dan inflasi dengan menggunakan model autoregressive distributed lag (ARDL). Penulis menyarankan untuk penelitian selanjutnya menggunakan variabel penelitian yang lebih banyak sehingga dapat memberikan hasil penelitian yang lebih baik. Model ARDL selain menggunakan pendekatan Koyck dapat juga dengan menggunakan pendekatan Almon.
DAFTAR PUSTAKA
Dornbusch, R., & Fischer, S. (1994).
Macroeconomics. Sixth Edition. New
York: The McGraw-Hill.
Gujarati, D. N. (2004). Basic Econometrics. Fourth Edition. New York: The McGraw-Hill.
Gujarati, D. N. (2006). Essentials of Econometrics. Third Edition. New York: The McGraw-Hill.
Lutkepohl, H., & Kratzig, M. (2005). New Introduction to Multiple Time Series Analysis. Berlin: Springer.
Nurahman, M. C., Wahyuningsih, S., &
Yuniarti, D. (2016). Model Dinamis: Autoregressive Dan Distribusi Lag, Studi Kasus Pengaruh Kurs Dollar Amerika Terhadap Produk Domestik Regional Bruto (PDRB). Jurnal Eksponensial, Vol. 07, No. 02, Hlm. 139-146.
Sarwoko. (2005). Dasar-Dasar Ekonometrika. Yogyakarta: Penerbit Andi.
Sembiring, R. K. (2003). Analisis Regresi. Edisi Kedua. Bandung: Penerbit ITB.
250
Discussion and feedback