PENERAPAN MODEL POPULASI KONTINU PADA PERHITUNGAN PROYEKSI PENDUDUK DI INDONESIA (STUDI KASUS: PROVINSI JAWA TIMUR)
on
E-Jurnal Matematika Vol. 9(4), November 2020, pp. 229-239
DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p303
ISSN: 2303-1751
PENERAPAN MODEL POPULASI KONTINU PADA PERHITUNGAN PROYEKSI PENDUDUK DI INDONESIA (STUDI KASUS: PROVINSI JAWA TIMUR)
Dewi Anggreini1§
1Program Studi Pendidikan matematika, Fakultas Sosial dan Humaniora, Universitas Bhinneka PGRI, Jl. Mayor Sujadi Timur No.7 Tulungagung, Indonesia [Email: anggreini1104@gmail.com] §Corresponding Author
ABSTRACT
The population data in Indonesia that is closest to the actual condition is only the data from the population census conducted by the Central Statistics Agency (BPS). The calculation of population projections in BPS throughout Indonesia uses the component method to see the projection of the population at the provincial level while the district level uses the geometric method with the assumption that the population will begin to increase geometrically with a basic reference for calculating compound interest. The purpose of this study is to determine population projections in the province of East Java using exponential and logistical models based on growth rates and carrying capacity. The data used in this study is secondary data, namely the population of the Central Statistics Agency (BPS) of East Java Province in 2012-2019. The data analysis technique is modeled by exponential model and logistic model. The best model is selected based on the results of the smallest MAPE value The results of this research are the carrying capacity value of East Java Province of 43,997,165.5 and the logistic model population growth rate of 0.05111. The conclusion of this research is that the most accurate model for estimating the population of East Java is the V logistic model because it has the smallest Mean Absolute Percentage Error (MAPE) value. This research is expected to be useful for users of population data in calculating future population projections.
Keywords: Carrying capacity, Exponential Model, Logistic Model, Population Projection
Permasalahan penting pada beberapa negara di dunia adalah mengenai proyeksi jumlah penduduk. Tren proyeksi jumlah penduduk, tingkat pertumbuhan, usia penduduk, urbanisasi dan migrasi merupakan variabel-variabel yang menjadi faktor penentu studi interdisipliner perubahan global di masa depan. O’Neil dkk (2001) pada suatu negara tingkat pertumbuhan populasi akan secara langsung berpengaruh terhadap kondisi ekonomi, politik, budaya dan pendidikan. Oleh sebab itu perlu dilakukan proyeksi jumlah penduduk di suatu wilayah termasuk di Jawa Timur.
Jawa Timur adalah salah satu provinsi yang memiliki kepadatan penduduk terbanyak dengan luas wilayah seluas 47.799, 75 km2 dan kepadatan penduduk di provinsi Jawa Timur tahun 2018 mencapai 826,39 jiwa/km2. (Badan Pusat Statistik, 2019). Berdasarkan data dari
BPS jumlah penduduk di Jawa Timur setiap tahunnya semakin bertambah, dari hal tersebut sangat dibutuhkan sebuah model proyeksi untuk menghitung jumlah penduduk di tahun mendatang yaitu salah satunya dengan model pertumbuhan populasi kontinu.
Bagian dari model pertumbuhan populasi kontinu adalah model eksponensial dan logistik. Kurniawan, Holisin, dan Kristanti (2017) menjelaskan model populasi kontinu berarti populasi bergantung waktu tanpa putus. Malthus mengemukakan tentang model eksponensial yaitu model pertumbuhan populasi yang menggambarkan sebuah populasi ideal dalam lingkungan yang tidak terbatas (Zabadi, Assaf dan Kanan, 2017). Hathout (2013) mengasumsikan laju pertumbuhan populasi proporsional dengan jumlah populasi pada model eksponensial.
Meskipun pendekatan model eksponensial efektif menghitung jumlah penduduk tetapi diperlukan pendekatan lain yang mengasumsikan terbatasnya sumberdaya dan situasi biologis. Hal ini mengarah pada model pertumbuhan yang dibatasi oleh sumberdaya dan situasi biologis tertentu yaitu model logistik (Winkel, 2011). Menurut Anggreini (2018) model logistik memasukkan batas untuk populasinya atau dibatasi oleh faktor penghambat dengan jumlah populasi tidak akan tumbuh berkembang secara tidak terhingga. Model logistik hingga sekarang masih dianggap paling mendekati dengan keadaan sebenarnya.
Beberapa penelitian yang mengkaji model logistik yaitu, Ofori, Ephraim, dan Nyarko (2013) menyimpulkan bahwa model logistik lebih akurat untuk memprediksi populasi penduduk di negara Ghana. Lukman dan Kwardiniya (2013) melakukan penelitian dengan menggunakan proyeksi model logistik untuk menghitung besarnya nilai carrying capacity, laju pertumbuhan, dan juga proyeksi jumlah penduduk di Surabaya dan Jakarta. Lindo Febdian & Efendi (2013) memperoleh hasil estimasi yaitu bahwa model logistik lebih akurat dalam menentukan proyeksi penduduk Sumatera Barat untuk waktu tertentu. Zuli Nuraeni (2015) juga menggunakan model eksponensial dan model logistik untuk memproyeksikan jumlah penduduk di Provinsi Maluku. Patel dan Prajapati (2016) menggunakan data pertumbuhan populasi aktual China dengan pendekatan model logistik untuk memperkirakan pertumbuhan populasi China. Kholipah, Anggriani & Supriatna (2017) menyimpulkan model logistik lebih akurat untuk pendugaan jumlah penduduk dikarenakan Model Verhulst dengan interval pengambilan sampel 12 tahun merupakan model dengan galat terkecil yaitu 1.410076124%.
Berdasarkan uraian pada bagian terdahulu, mengingat Provinsi Jawa Timur merupakan provinsi dengan jumlah penduduk terbanyak nomor 2 setelah Jakarta, maka penulis tertarik untuk melakukan proyeksi jumlah penduduk di Provinsi Jawa Timur dengan menggunakan estimasi model eksponensial dan model logistik.
Model eksponensial merupakan model yang sangat tepat dalam memproyeksikan pertumbuhan populasi pada kondisi ideal, akan tetapi sebuah model akan lebih realistik jika mencerminkan fakta bahwa suatu lingkungan memiliki sumber daya yang terbatas. Oleh karenanya diperlukan model populasi logistik
untuk memproyeksikan jumlah penduduk di Jawa Timur. Dengan demikian tujuan penelitian ini adalah menentukan besarnya laju pertumbuhan serta besarnya jumlah penduduk pada tahun 2030 dengan model eksponensial, laju pertumbuhan dan besarnya jumlah penduduk dengan model logistik. Selanjutnya dicari model yang paling akurat yang memiliki nilai galat terkecil menggunakan Mean Absolute Percentage Error (MAPE) dengan alat bantu program Excel dan MAPLE.
Persamaan diferensial merupakan sebuah persamaan yang terdiri dari satu atau lebih turunan dari sebuah fungsi yang tidak diketahui (Rustanto, 2003). Persamaan diferensial dapat ditulis dengan rumus sebagai berikut : do (x)y(n)+a1 (x)y( n-1)+..+ (X)y=(X),
(1)
dengan aO , O1,…, dan F fungsi dari X dan «0 (X)≠0 dinamakan persamaan diferensial linear orde n. Persamaan tersebut linear dalam y', y”,...,y(n).
Castillo-Chavez (2000) menyebutkan r adalah laju pertumbuhan intrinsik atau laju pertumbuhan perkapita jika ukuran poapulasi kecil dari sumber yang terbatas. Kerry dkk (2017) menyatakan laju pertumbuhan intrinsik merupakan laju di mana suatu populasi bertambah besar jika tidak ada gaya yang bergantung pada kepadatan yang mengatur populasi. Jika ( ) adalah laju kenaikan
populasi, N ukuran populasi, dan r adalah tingkat peningkatan intrinsik maka berlaku hubungan:
1 dN
=
N dt
Modifikasi persamaan logistik mempunyai bentuk at = (1-K ) dengan K= . r adalah laju pertumbuhan dan K adalah batas pertumbuhan populasi. K disebut juga sebagai saturation level. Jadi K merupakan carrying capacity dari suatu wilayah pada populasi (Wei, Jiang & Zang. 2015) dan nilai r adalah laju pertumbuhan intrinsik yang menggambarkan daya tumbuh populasi. Carrying capacity dapat dicari dari hasil nilai limit:
N( t ) max= lim N(t)= ≡ → ∞ b
N1 (IN0N2-N2N1-N0N1) N0N2-N12
(2)
Model pertumbuhan penduduk dengan model eksponensial dan logistik terkenal dalam menentukan pertumbuhan populasi. Model eksponensial memberi gambaran pertumbuhan
populasi di lingkungan ideal dengan sumber daya alam yang tidak terbatas. (Zabadi, Assaf, dan Kanan. 2017). Model eksponensial diperkenalkan oleh Malthus pada tahun 1978 yang dikenal dengan model pertumbuhan (Malthus. 1992). Nuraeni (2015) menyebutkan model eksponensial digunakan untuk mengestimasi populasi dengan laju pertumbuhan konstan, p( t) melambangkan jumlah populasi yang bertambah. Jika diasumsikan P(t) adalah fungsi yang bisa diturunkan terhadap sebuah waktu, termasuk fungsi kontinu, maka dapat diasumsikan ^, laju perubahan populasi proporsional terhadap jumlah populasi yang ada. (Zabadi, Assaf, dan Kanan. 2017).
Stephano & Hyo (2019) menyebutkan model eksponensial memiliki pertumbuhan populasi pada laju yang konstan dan laju proporsional pada ukuran populasi asli. Hal ini wajar pada kondisi ideal yang tidak terbatas lingkungan, nutrisi yang memadai, tidak adanya predator dan kekebalan dari penyakit yang tidak termasuk pada model. Model ini menggambarkan bahwa populasi akan bertambah dengan laju pertumbuhan yang sebanding dengan banyaknya populasi
Jika N(t) besarnya populasi saat t maka model eksponensial dinyatakan:
-
— rN = 0 atau = rN t t). (3)
dt dt y j v 7
N(t) adalah kerapatan populasi (banyaknya populasi dalam waktu t jam), No adalah banyaknya populasi mula-mula dan t adalah waktu ke t (jam) dengan r adalah laju pertumbuhan (Malthusian Parameter). (Ullah dkk. 2019). Berkurangnya daya dukung akibat pertumbuhan dan populasi yang terus mengalami kenaikan sehingga model Malthus
= r N t t) perlu dimodifikasi. Bila N membesar dan wilayah terbatas maka, akan muncul permasalahan dikarenakan padatnya sebuah populasi (Susanta. 2008). Tarumingkeng (1994) mengasumsikan f (N) adalah merupakan fungsi linear, yakni a adalah faktor dari penurunan proporsional.
f (N) = r — aN , r,« > 0, N > 0, dN
= N(r — aN)
Clt
^ = r — a N, persamaan ini disebut model Verhulst-pearl.
— = rN t t) adalah persamaan diferensial separabel dengan solusi umumnya:
N (t) = er t+c (4)
Jika nilai mula-mula t = 0 dan N(0) = N0 maka akan diperoleh nilai c = ln N0, Kemudian jika c disubstitusikan ke (4) maka
N (t) = Nerrt (5)
Persamaan (5) merupakan solusi khusus model eksponensial. Jika r bernilai positif populasi menjadi meningkat secara eksponensial dan apabila r bernilai negatif maka populasi akan menjadi punah.
Model Logistik merupakan sebuah model yang menggunakan faktor logistik yaitu faktor makanan dan faktor ruang hidup. Model tersebut adalah sebuah inovasi dari model eksponensial yang dicetuskan oleh Maltus (Huberman. 1977). Model logistik merupakan model modifikasi dari model eksponensial (Mondol, Mallick dan Biswas. 2018). Model ini diperkenalkan oleh Verhulst pada tahun 1845. (Wei, Jiang dan Zhang. 2015). Castillo-Chavez (2000) model logistik diasumsikan dengan jumlah rata-rata pertumbuhan yang bergantung pada besarnya populasi atau laju pertumbuhan perkapita.Jumlah populasi pada waktu tertentu akan mendekati titik equilibrium. Tarumingkeng (1994) Model logistik akan memiliki sebaran umur yang stabil dengan cara mencari keseimbangan lingkungan.
Berbeda dengan model eksponensial, yang mempunyai batas terhadap populasinya sehingga akan bertambah secara tak terhingga dikarenakan jumlah populasi selalu terbatas pada sebuah nilai tertentu. Penggunaan model logistik dikarenakan pada realita dialam besar kecilnya populasi tergantung kepada kepadatannya sehingga laju kelahiran dan kematian tidak konstan (Huberman. 1977).
Penyimpangan terhadap data-data populasi sangatlah kecil dengan kata lain memiliki kemiripan dengan data yang sebenarnya. Pada posisi tersebut jumlah kematian dan kelahiran dianggap sama sehingga pada grafik mengarah mendekati konstan. Bentuk sederhana pada laju pertumbuhan yang mengakomodasi asumsi tersebut adalah:
A^ = k(1--} (6)
Persamaan (6) jika dikalikan N maka akan
diperoleh model persamaan diferensial logistik.
dN N∖
= (1- )
dt k κ)
(7)
Dengan r laju pertumbuhan dan K adalah daya tampung populasi yang membatasi pertumbuhan populasi saat t→∞, N adalah ukuran populasi. Model ini memiliki bentuk kurva sigmoid dan memiliki pertumbuhan populasi seperti model eksponensial, diikuti pengurangan pertumbuhan, dan dibatasi daya dukung karena tekanan faktor ekologis. (Ullah dkk. 2019) Dari persamaan (7) bahwa jika N Jauh lebih kecil daripada K, maka N/K mendekati 0 dan dN/dt ⅛ rN. Jika N→K (populasi semakin mengarah pada kapasitas tampung), sehingga N/K→ 1, maka → 0. Jika populasi N berada diantara 0 dan K, maka ruas kanan bernilai dengan catatan r positif, sehingga → 1 Populasi menjadi naik.
Apabila populasi melebihi beban tampung (N> K), 1- bernilai negatif, maka <0
sehingga populasi akan turun. Solusi persamaan logistik yaitu:
Kert+c
N= l+ert+c (8)
Dari persamaan (6) apabila ditambahkan nilai awal t = 0 dan N (0) = N0 lalu disubstitusikan
ke (7) maka akan diperoleh nilai c = ln (N0/ K -
N0) selanjutnya nilai c disubstitusikan ke (8),
diperoleh solusi khusus model logistik yaitu,
K
(⅛1)+ 1
N(t)=
(9)
N diartikan sebagai jumlah populasi ketika t. N0 jumlah populasi awal saat t = 0. K diartikan sebagai daya tampung populasi. r diartikan sebagai laju pertumbuhan dan t diartikan sebagai waktu. Persamaan (9) merupakan bentuk sederhana model logistik untuk proyeksi penduduk.
Nilai galat dihitung dengan MAPE (Mean Absolut Persentage Error) yaitu MAPE.= - ∑|Xi_Fi |X100%. =
n xi L
data sebenarnya,
= data hasil prediksi.
Nilai MAPE terkecil merupakan yang terbaik
karena persentase errornya lebih kecil yang dihasilkan dari sebuah model. Penjelasan tentang nilai MAPE diuraikan dalam Tabel 1.
Tabel 1. Indikator Nilai MAPE
|
<10% |
Sangat Akurat |
|
10% - 20% |
Sangat Baik |
|
21%-50% |
Masuk Akal |
|
>51% |
Tidak Akurat |
Penelitian ini termasuk jenis penelitian
deskriptif dengan rancangan studi kasus. Penelitian menggunakan data sekunder dari BPS Provinsi Jawa Timur yaitu data jumlah penduduk Provinsi Jawa Timur tahun 2012 hingga tahun 2019.
Pada tahapan metode riset langkah-langkah yang digunakan diantaranya menentukan subjek penelitian, mengumpulkan data penelitian, selanjutnya menganalisis data dan terakhir menarik kesimpulan.
Adapun teknik analisis data yang digunakan adalah sebagai berikut:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Mengkonstruksi model eksponensial dan
logistik,
Mencari solusi = (t) dan
dN N.
= (1- )
dt k K7
Mencari waktu saat t,
Menghitung jumlah populasi awal serta populasi pada tahun selanjutnya, Menentukan carrying capacity, Menentukan Laju pertumbuhan,
Menghitung jumlah penduduk dengan model logistik,
Membandingkan seberapa akurat nilai hasil estimasi penduduk menggunakan model ekponensial dan logistik
Membandingkan hasil perhitungan yang mendekati galat terkecil dengan data sebenarnya
10. Menentukan proyeksi jumlah penduduk di Provinsi Jawa Timur tahun 2030.
Dalam melakukan proyeksi penduduk di Provinsi Jawa Timur perlu dilakukan terlebih dahulu analisis perhitungan terhadap jumlah penduduk di Provinsi Jawa Timur agar dapat diketahui pola dan banyaknya data yang digunakan (Khakim. 2011). Jumlah data yang digunakan turut memengaruhi keakuratan model dalam memprediksi kondisi jumlah populasi secara menyeluruh. Adapun data penelitian yang diambil dari Badan Pusat Statistik (BPS) di Provinsi Jawa Timur, secara ringkas dapat
dilihat pada Tabel 2 berikut:.
Tabel 2. Jumlah Penduduk di Jawa Timur Tahun 2012-2019
|
Waktu |
Tahun |
Jumlah Penduduk |
Tahun (N) |
|
t=0 |
2012 |
38,106,590 |
N0 |
|
t=1 |
2013 |
38,363,195 |
N1 |
|
t=2 |
2014 |
38,610,202 |
N2 |
|
t=3 |
2015 |
38,847,561 |
N3 |
|
t=4 |
2016 |
39,075,152 |
N4 |
|
t=5 |
2017 |
39,292,972 |
N5 |
|
t=6 |
2018 |
39,500,851 |
N6 |
|
t=7 |
2019 |
39,698,631 |
N7 |
Berdasarkan data pada Tabel 2, dilakukan proyeksi penduduk di Provinsi Jawa Timur dengan menggunakan model logistik dengan diasumsikan t = 0 pada tahun 2012 maka syarat awal N(0) = 38.106.590. Nilai carrying capacity dapat dihitung menggunakan persamaan dibawah ini:
N(t)Max - lim → ∞N(t)= =
^(2N0N2-N2N1-N0N1)
N0N2-N12
Dari tabel 1 diperoleh t = 0, 1, 2 tahun 2012, 2013, 2014 dengan N0 , , adalah
N0 = 3810,6590,
N1, = 38363195, N2 = 38610202
Nq , , disubstitusikan ke persamaan
diperoleh nilai carrying capacity yaitu = 43.997.165,6
K dan N0 didistribusikan ke solusi (9) diperoleh
= . 997 . 165 ,6— .
= (o,15458)+1 , (10)
Dari persamaan (10) dicari model logistik yang mewakili laju pertumbuhan untuk t=1 pada
tahun 2013 maka N(1) = 38.363.195, jika didist:ribusikan ke (10) diperoleh r = 0,05124, Nilai r disubstitusikan ke (10) maka:
— 43.997.165,6 f 1 1 T\
= (0,15458 .) τ(. ,051 , )t +1 , (Model I)
-
1. Model Logistik I yaitu
= (0,15458 .) T(. ,051 , )t +1 dengan laju pertumbuhan relatif 5,12%
-
2. Model Logistik II yaitu
=(0,15458)T (. 0,05, )t + l dengan laju
pertumbuhan relatif 5,12%
-
3. Model Logistik III yaitu
=(0,15458)T (. 0,05, )t + l dengan laju
pertumbuhan relatif 5,12%
-
4. Model Logistik IV yaitu
=(0,15458)T (. 0,05118)t + l , dengan laju pertumbuhan relatif 5,1%
-
5. Model Logistik V, yaitu
=(0,15458)T (. 0,05111)t + l , dengan laju pertumbuhan relatif 5,1%
-
6. Model Logistik VI yaitu
=(0,15458)T (. 0,05, )t + l , dengan laju
pertumbuhan relatif 5,1%
-
7. Model Logistik VII yaitu
=(0,15458) τ- (. 0,05, )t + l dengan laju
pertumbuhan relatif 5,08%.
Berdasarkan tujuh model yang diperoleh, dan jumlah penduduk pada Tabel 2 dapat dihitung proyeksi jumlah penduduk dengan
menggunakan model 1, 2, 3,..., 7 yang secara lengkap dapat dilihat pada Tabel 3. Pada Tabel 3 dapat dilihat perbandingan jumlah penduduk realnya dengan hasil proyeksi di Provinsi Jawa Timur dari tahun 2012 sampai tahun 2019.
Tabel 3. Perbandingan Jumlah Penduduk Jawa Timur antara Hasil Sensus dan Hasil Model Logistik
|
TAHUN |
HASIL SENSUS |
MODEL I |
MODEL II |
MODEL III |
MODEL IV |
MODEL V |
MODEL VI |
MODEL VII |
|
2012 |
38,106,590 |
38,106,641 |
38,106,641 |
38,106,641 |
38,106,641 |
38,106,641 |
38,106,641 |
38,106,641 |
|
2013 |
38,363,195 |
38,363,192 |
38,363,241 |
38,363,192 |
38,362,904 |
38,362,551 |
38,362,030 |
38,361,310 |
|
2014 |
38,610,202 |
38,610,149 |
38,610,244 |
38,610,149 |
38,609,595 |
38,608,916 |
38,607,912 |
38,606,527 |
|
2015 |
38,847,561 |
38,847,734 |
38,847,871 |
38,847,734 |
38,846,935 |
38,845,955 |
38,844,507 |
38,842,508 |
|
2016 |
39,075,152 |
39,076,177 |
39,076,352 |
39,076,177 |
39,075,152 |
39,073,896 |
39,072,040 |
39,069,477 |
|
2017 |
39,292,972 |
39,295,711 |
39,295,921 |
39,295,711 |
39,294,481 |
39,292,972 |
39,290,742 |
39,287,664 |
|
2018 |
39,500,851 |
39,506,578 |
39,506,819 |
39,506,578 |
39,505,159 |
39,503,421 |
39,500,851 |
39,497,303 |
|
2019 |
39,698,631 |
39,709,018 |
39,709,289 |
39,709,018 |
39,707,430 |
39,705,483 |
39,702,605 |
39,698,631 |
Selanjutnya, dilakukan proyeksi penduduk dengan menggunakan Model Eksponensial. Model Eksponensial untuk menentukan proyeksi penduduk adalah: = (t). Solusi
Umum dari model adalah: N(t)=
-
1 Nt
N0ekt, dengan k=
-
a. Model Eksponensial I bentuk persamaannya,
N(t) = 38.106.590e(0, 00670 )t
-
b. Model Eksponensial II bentuk persamaannya,
N(t) = 38.106.590e(0, 00656 ) t
-
c. Model Eksponensial III bentuk persamaannya,
N(t) = 38.106.590e(0, 00641 )t
-
d. Model Eksponensial IV bentuk persamaannya,
N(t) = 38.106.590e(0, 00627 )t
-
e. Model Eksponensial V bentuk persamaannya,
N(t) = 38.106.590e(0, 00613 )t
-
f. Model Eksponensial VI bentuk
persamaannya,
N(t) = 38.106.590e(0, 00599 )t
-
g. Model Eksponensial VII bentuk
persamaannya,
N(t) = 38.106.590e(0, 005847 ) t
Setelah diketahui bentuk persamaan untuk setiap model eksponensial dari model I hingga model VII, kemudian dilakukan perbandingan antara jumlah penduduk yang sebenarnya dengan hasil model eksponensial. Adapun perbandingannya disajikan dalam bentuk Tabel 4.
Tabel 4. Perbandingan Jumlah Penduduk Antara Hasil Sensus dan Hasil Model Eksponensial
|
TAHUN |
HASIL SENSUS |
MODEL I |
MODEL II |
MODEL III |
MODEL IV |
MODEL V |
MODEL VI |
MODEL VII |
|
2012 |
38,106,590 |
38,106,590 |
38,106,590 |
38,106,590 |
38,106,590 |
38,106,590 |
38,106,590 |
38,106,590 |
|
2013 |
38,363,195 |
38,362,761 |
38,357,391 |
38,351,638 |
38,346,269 |
38,340,901 |
38,335,501 |
38,330,054 |
|
2014 |
38,610,202 |
38,620,655 |
38,609,843 |
38,598,261 |
38,587,455 |
38,576,652 |
38,565,788 |
38,554,829 |
|
2015 |
38,847,561 |
38,880,282 |
38,863,956 |
38,846,471 |
38,830,159 |
38,813,854 |
38,797,458 |
38,780,922 |
|
2016 |
39,075,152 |
39,141,655 |
39,119,741 |
39,096,277 |
39,074,389 |
39,052,513 |
39,030,519 |
39,008,341 |
|
2017 |
39,292,972 |
39,404,784 |
39,377,210 |
39,347,689 |
39,320,155 |
39,292,640 |
39,264,981 |
39,237,094 |
|
2018 |
39,500,851 |
39,669,683 |
39,636,374 |
39,600,717 |
39,567,467 |
39,534,244 |
39,500,851 |
39,467,188 |
|
2019 |
39,698,631 |
39,936,362 |
39,897,243 |
39,855,373 |
39,816,334 |
39,777,333 |
39,738,138 |
39,698,631 |
Lebih lanjut lagi, menghitung galat nilai proyeksi jumlah penduduk dengan menggunakan MAPE. Terlebih dahulu dihitung galat model eksponensial, Adapun nilai galat yang diambil adalah dengan nilai galat terkecil yang terletak pada Model Eksponensial V
dengan persamaan:
N(t) = 38.106.590e(0, 00613 )t.
Model ini digunakan untuk memprediksi jumlah penduduk Provinsi Jawa Timur diperoleh N(t = 18) = 42.552.016. Jumlah penduduk Provinsi Jawa Timur pada tahun 2030
berdasarkan model eksponensial adalah sebesar 42.552.016 jiwa. Hasil perhitungan galat model eksponensial dalam % disajikan dalam Tabel 5.
Tabel 5. Galat Model Eksponensial dalam Persen (Absolute Percent Error)
|
TAHUN |
GALAT MODEL I |
GALAT MODEL II |
GALAT MODEL III |
GALAT MODEL IV |
GALAT MODEL V |
GALAT MODEL VI |
GALAT MODEL VII |
|
2012 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2013 |
0.00113 |
0.01513 |
0.03013 |
0.04412 |
0.05811 |
0.07219 |
0.08639 |
|
2014 |
0.02707 |
0.00093 |
0.03093 |
0.05891 |
0.08689 |
0.11503 |
0.14341 |
|
2015 |
0.08423 |
0.04220 |
0.00281 |
0.04480 |
0.08677 |
0.12897 |
0.17154 |
|
2016 |
0.17019 |
0.11411 |
0.05406 |
0.00195 |
0.05794 |
0.11422 |
0.17098 |
|
2017 |
0.28456 |
0.21439 |
0.86075 |
0.06918 |
0.00084 |
0.07124 |
0.14221 |
|
2018 |
0.42741 |
0.34309 |
0.25282 |
0.16864 |
0.08454 |
0.00000 |
0.08522 |
|
2019 |
0.59884 |
0.50030 |
0.39483 |
0.29649 |
0.19825 |
0.09952 |
0.00000 |
|
∑ Galat /n |
0.199 |
0.154 |
0.203 |
0.086 |
0.072 |
0.075 |
0.100 |
Berdasarkan Tabel 4 kita telah mengetahui bahwa galat model eksponensial yang terkecil adalah galat model V, kemudian akan kita bandingkan lagi dengan hasil galat model logistik dengan menggunakan MAPE
(Mean Absolut Persentage Error), Adapun rincian hasil perhitungan galat model logistik untuk setiap model dari tahun 2012 hingga tahun 2019 disajikan dalam Tabel 6.
Tabel .6 Galat Model Logistik dalam Persen
|
TAHUN |
MODEL I |
MODEL II |
MODEL III |
MODEL IV |
MODEL V |
MODEL VI |
MODEL VII |
|
2012 |
0.000134 |
0.000134 |
0.000134 |
0.000134 |
0.000134 |
0.000134 |
0.000134 |
|
2013 |
0.000007 |
0.000121 |
0.000007 |
0.000758 |
0.001678 |
0.003037 |
0.004912 |
|
2014 |
0.000136 |
0.000109 |
0.000136 |
0.001572 |
0.003331 |
0.005930 |
0.009518 |
|
2015 |
0.000447 |
0.000798 |
0.000447 |
0.001612 |
0.004134 |
0.007862 |
0.013007 |
|
2016 |
0.002623 |
0.003070 |
0.002623 |
0.000000 |
0.003214 |
0.007965 |
0.014523 |
|
2017 |
0.006972 |
0.007506 |
0.006972 |
0.003839 |
0.000000 |
0.005674 |
0.013508 |
|
2018 |
0.014497 |
0.015110 |
0.014497 |
0.010907 |
0.006505 |
0.000000 |
0.008982 |
|
2019 |
0.026165 |
0.026847 |
0.026165 |
0.022164 |
0.017260 |
0.010011 |
0.000000 |
|
∑ Galat /n |
0.006373 |
0.006712 |
0.006373 |
0.005123 |
0.004532 |
0.005077 |
0.008073 |
Hasil perhitungan Tabel 6 dapat diketahui bahwa model galat logistik yang terkecil berada pada model V. Nilai dari MAPE yang paling kecil adalah nilai paling baik dikarenakan persentase errornya paling kecil. Diperoleh nilai MAPE terkecil yaitu 0,004532. Dalam memprediksi jumlah penduduk di Provinsi Jawa Timur Tahun 2030 dengan melihat Nilai MAPE dan model Logistik V yaitu sebesar 0,004532
dipakai dalam memperkirakan jumlah penduduk. Misalkan t = 18 disubstitusikan pada model logistik V diperoleh: N = 41.444.035. Diperoleh jumlah penduduk Provinsi Jawa Timur tahun 2030 dari model logistik sebesar 41.444.035. Adapun gambaran diagram Jumlah Penduduk Provinsi Jawa Timur antara hasil sensus dan hasil model ditampilkan dalam bentuk Grafik 1.
dan
=
43.997.165,6
(O,15458)e(0,05111)t + l
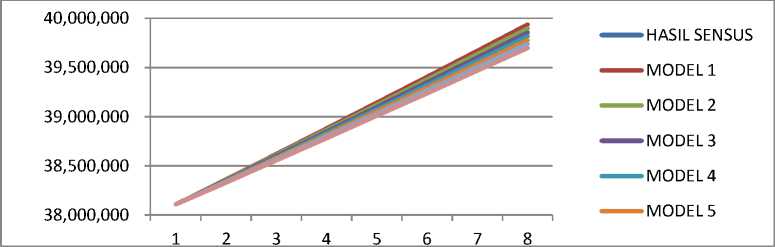
Grafik 1. Jumlah Penduduk Jawa Timur antara hasil sensus dan model eksponensial
40,000,000
39,500,000
39,000,000
38,500,000
38,000,000
HASIL SENSUS
MODEL 1
MODEL 2
MODEL 3
MODEL 4
MODEL 5
MODEL 6
MODEL 7
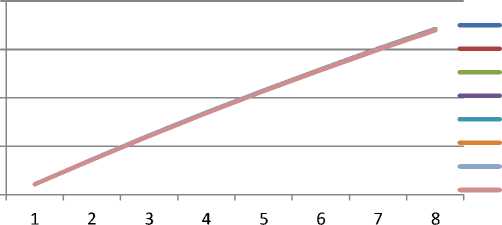
Grafik 2 Perbandingan Jumlah Penduduk antara hasil sensus dan model logistik
Berdasarkan Grafik 1 dan 2 model logistik lebih akurat dalam menggambarkan jumlah penduduk dikarena model logistic dapat memberikan hasil yang lebih mendekati hasil sensus dibandingkan dengan hasil model eksponensial. Dari nilai MAPE diperoleh model eksponensial V dan model logistik V yang memiliki nilai galat paling kecil dibandingkan model lain. Perhitungan Mean Absolut Persentage Error (MAPE) diperoleh nilai galat model eksponensial V sebesar 0,072 sedangkan nilai galat model logistik V sebesar 0,004532. Sehingga dua model tersebut akurat digunakan untuk memprediksi jumlah penduduk karena memiliki nilai galat yang kecil. Akan tetapi berdasarkan tujuan penelitian yaitu mencari model yang paling akurat yang memiliki nilai MAPE terkecil untuk memprediksi jumlah penduduk maka dipilih model Logistik V.
Model eksponensial dan logistik sebenarnya sama-sama mendekati data sensus sehingga bisa digunakan untuk memproyeksikan jumlah penduduk. Model logistik V memiliki nilai yang lebih akurat dalam menggambarkan jumlah penduduk dikarenakan menghasilkan angka yang mendekati dengan hasil sensus dibandingkan dengan model eksponensial.
Berikut akan diberikan proyeksi penduduk Provinsi Jawa Timur menggunakan model eksponensial dengan pengambilan waktu
t = 0,1,2,3..,18. Grafik 3 dan 4 menunjukkan pertumbuhan penduduk Provinsi Jawa Timur dari t=0 hingga t=18 selalu mengalami kenaikan
Zrafikperrumbuhan eksponensial
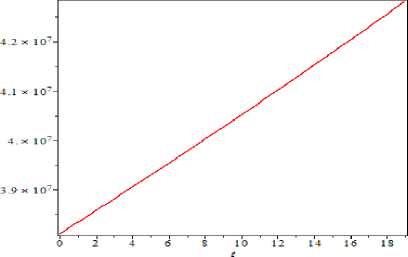
Grafik 3. Proyeksi penduduk dengan t=0,1,2,..,18
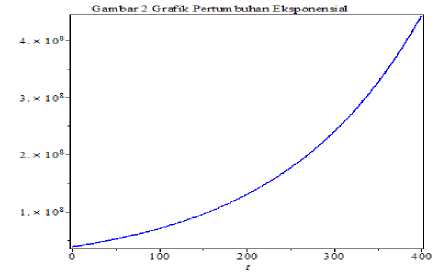
Grafik 4. Proyeksi Penduduk Provinsi Jawa
Timur dengan t = 0,1,2,3,..,400
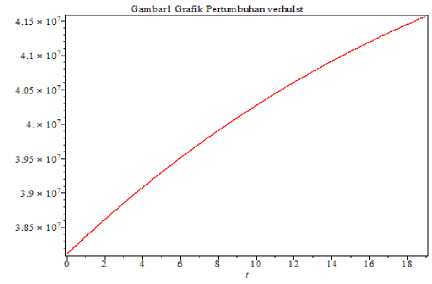
Grafik 5. Proyeksi Pertumbuhan Penduduk Di Provinsi Jawa Timur dengan t = 0,1,2,..,18
Proyeksi penduduk Provinsi Jawa Timur menggunakan model logistik dengan pengambilan t = 0,1,2,..,18. Grafik 5 menunjukkan adanya kenaikan jumlah penduduk dari waktu ke waktu di Provinsi Jawa Timur
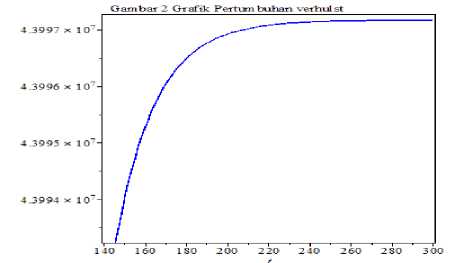
Grafik 6. Proyeksi Pesrtumbuhan Penduduk Di Provinsi Jawa Timur dengan t = 0.1,2,..,.300
Berdasarkan grafik 6 dapat dilihat bahwa di Provinsi Jawa Timur selalu mengalami kenaikan dari waktu ke waktu, akan tetapi pada waktu yang akan datang jumlah penduduk tidak akan melebihi carrying capacity melainkan mendekati nilai carrying capacity. Jadi untuk waktu yang akan datang jumlah penduduk Provinsi Jawa Timur akan mendekati nilai K = 43.997.165,6.
Nilai galat terkecil MAPE (Mean Absolut Persentage Error) merupakan nilai galat yang terbaik, dikarenakan prosentase erronya lebih kecil dan dihasilkan dari estimasi model logistik V sebesar 0,004532. Hal ini sesuai dengan pendapat Ofori dkk (2013) yaitu untuk interpretasi nilai MAPE yang kurang dari 10%
adalah proyeksi yang sangat akurat. Sehingga model Logistik V sangat tepat diterapkan untuk memproyeksikan jumlah penduduk di Jawa Timur pada tahun 2030 dengan jumlah penduduk sebesar 41.444.035 jiwa dan laju pertumbuhan r = 0,05111. Hasil penelitian ini sesuai juga dengan Mondol, Mallick & Biswas (2018) yang menyimpulkan bahwa model logistik memiliki persentase kesalahan mutlak (MAPE) yang sangat rendah dibandingkan dengan model eksponensial. Sehingga model Logistik memberikan hasil peramalan yang lebih baik untuk prediksi jangka panjang. Hal ini sesuai dengan Kurniawan, Holisin dan Kristanti (2017) yang menyatakan meskipun model eksponensial dan logistik sama-sama memiliki nilai galat terkecil tetapi yang lebih akurat dan memiliki galat lebih kecil adalah model logistic.
Penemuan ini sejalan dengan Putri, Widya (2015) yang menyimpulkan bahwa dalam memprediksi jumlah penduduk dengan menggunakan pendekatan model Malthus dan model Verhulst dengan cara menghitung rata-rata galat mutlak masing-masing model bahwa untuk menghitung estimasi jumlah penduduk berdasarkan jenis kelamin dan kelompok umur yang tepat adalah model verhulst. Sejalan juga dengan Febdian, Lindo & Efendi (2013) menyimpulkan bahwa model geometri dan logistik memiliki nilai galat terkecil dibanding model lain. Model geometri tidak relevan apabila diterapkan dalam jangka waktu yang cukup lama, sedang model logistik lebih akurat digunakan untuk menghitung proyeksi jumlah penduduk pada waktu yang akan datang. Ullah dkk (2019) juga mendefinisikan bahwa hasil proyeksi penduduk untuk jangka waktu yang akan datang berdasarkan perhitungan menggunakan model logistik mendekati hasil sensus penduduk.
Proyeksi pertumbuhan penduduk Provinsi Jawa Timur mengalami kenaikan jumlah penduduk tetapi tidak akan melebihi melainkan mendekati nilai carrying capacity. Jadi untuk waktu mendatang yang akan datang jumlah penduduk Provinsi Jawa Timur akan mendekati nilai K = 43.997.165,6. Hal ini sesuai dengan Kucharavy, Dmitry & De Guio, Roland (2015) yang menjelaskan bahwa nilai K adalah tingkat kejenuhan (saturation level) yaitu limit pertumbuhan asimtotik (asymtotic limit of growth) dalam kurva model logistik. Nilai koefisien vital a dan b untuk memperoleh nilai K membatasi pertumbuhan populasi penduduk
disuatu daerah atau negara (Mondol, Mallick dan Biswas. 2018). Jadi nilai limit pertumbuhan asimtotik penduduk Provinsi Jawa Timur adalah sebesar 43.997.165,6.
-
5. KESIMPULAN
Berdasarkan hasil analisa dapat disimpulkan bahwa:
Laju pertumbuhan penduduk (r) di Provinsi Jawa Timur menggunakan model eksponensial adalah sebesar 0,00613 dengan (Nt)= 38.106.590e(0, 00613 )t, sedangkan dengan
menggunakan model logistik laju
pertumbuhannnya (r) adalah sebesar 05111. Jumlah penduduk Provinsi Jawa Timur tahun 2030 dengan estimasi model eksponensial V adalah sebesar 42.552.016. Sedangkan dengan menggunakan estimasi model logistik V adalah sebesar 41.444.035. Nilai carrying capacity (K) = 43.997.165,6.
Model paling akurat untuk estimasi jumlah penduduk Provinsi Jawa Timur tahun 2030 adalah model logistik V berdasarkan nilai
D L Y 1 Y m ⅛+ l 1 • 43.997.165,6
MAPE terkecil yaitu: = ( ) .
(0,15458) ( , )
Proyeksi jumlah penduduk Provinsi Jawa Timur berdasarkan grafik model eksponensial menunjukkan pertumbuhan penduduk
mengalami kenaikan. Proyeksi pertumbuhan penduduk model logistik tidak akan melebihi nilai carrying capacity 43.997.165,6.
Peneliti lain bisa mengembangkan penelitian ini untuk mencari analisis kestabilan lokal dari model persamaan logistik untuk jangka waktu yang akan datang. Hal ini dikarenakan dalam penelitian ini belum membahas kestabilan dari model.
UCAPAN TERIMAKASIH
Penulis mengucapkan terimakasih atas bantuan dari LPPM dan Universitas Bhinneka PGRI atas bantuan hibah penelitian sehingga penelitian ini berjalan dengan lancar dan sukses.
DAFTAR PUSTAKA
Anggreini. 2018. Model Matriks Leslie dengan Strategi Pemanenan pada Kelompok Umur Termuda pada Angka Kesuburan dan Harapan Hidup Populasi Domba Betina. Fourier. 7 (1). 23-34.
Badan Pusat Statistik. 2019.Provinsi Jawa Timur Dalam Angka (Jawa Timur Province in Figures), Surabaya.
Brian J. Winkel. 2011. Parameter Estimates in Differential Equation Models for Population Growth, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 21:2, 101-129.
Brauer, F., Castillo-Chavez, C. 2000. Mathematical Models in Population Biology and Epidemiology. Edisi 2. Newyork:
Springer.
C.C. Kerry, Tessy S, Ezeora J.N, Iweanandu O.J. 2017. A Comparative Study of Mathematical and Statistical Models for Population Projection of Nigeria. International Journal of Scientific & Engineering Research, 8 (2).
Febdian, Lindo & Efendi. 2013. Menentukan Model Pertumbuhan Penduduk Provinsi Sumatera Barat, Jurnal Matematika UNAND,2(4).54-58.
Hasibuan,K.M. 1988. Pemodelan Matematika di dalam Biologi Populasi (Dinamika Populasi). Bogor: Pusat antar Universitas, Institut Pertanian Bogor bekerja sama dengan Lembaga Sumberdaya Informasi-IPB.
Hathout, Dean. 2013. Modeling Population
Growth: Exponential and Hyperbolic
Modeling. Applied Mathematics. 4, 299304.
Huberman. AM. 1977. (2nd Impression) Solving Educational Problems, The Theory and Reality on Innovation in Developping Countries. Paris, Unersco.
Khakim L. 2011. Proyeksi Penduduk Provinsi DKI Jakarta dan Kota Surabaya dengan Model Pertumbuhan Logistik. Universitas Brawijaya: Malang.
Khaqim, Luqman dan Andawaningtyas, Kwardiniya. 2013. Proyeksi Penduduk Provinsi DKI Jakarta dan Kota Surabaya dengan Model Pertumbuhan Logistik. Jurnal Matematika Mahasiswa. 1 (3). 232-235.
Kurniawan, A., Holisin, I., & Kristanti, F. 2017. Aplikasi Persamaan Diferensial Biasa Model Eksponensial dan Logistik pada Pertumbuhan Penduduk Kota
Surabaya. MUST: Journal of Mathematics Education, Science and Technology, 2(1), 129-141.
Kucharavy, Dmitry & De Guio, Roland. 2015. Application of Logistic Growth Curve. Procedia Engineering. 131. 280 – 290.
Malthus, T. R., Winch, D., & James, P. 1992. Malthus:'An Essay on the Principle of Population'. Cambridge University Press.
Mondol. H, Mallick UK, Biswas MAH .2018. Mathematical Modeling And Predicting The Current Trends Of Human Population Growth In Bangladesh. Advances In
Modelling And Analysis A.55 (2). 62-69.
Nuraeni, Zuli. 2015. Aplikasi Persamaan
Diferensial dalam Estimasi Jumlah Populasi, Jurnal Ilmiah Pendidikan Matematika. 5(1) 9-16.
Nurkholipah N.S, Anggriani, N & Supriatna, AK. 2017. Perbandingan Proyeksi Penduduk Jawa Barat Menggunakan Model Malthus dan Verhulst dengan Variasi Interval Pengambilan Sampel. Prosiding SI MaNIs (Seminar Nasional Integrasi Matematika dan Nilai Islami).,1 (1). 195-202.
Ofori, T, dkk. 2013. Mathematical Model of Ghana’s Population Growth, International Journal of Modern Management Sciences. 2(2). 57-66.
O’Neil BC, Balk D, Brickman M, Ezra M. 2001. A Guide To Global Population Projections..Demographic Research. 4(8), 203-288.
Patel, A.J & Prajapati, M.B. 2016. Estimation for Future Population Growth of China by using Logistic model. IJDR. 1(9).52-56.
Putri, Widya. 2015. Perbandingan Model
Malthus Dan Model Verhulst Untuk
Estimasi Jumlah Penduduk Indonesia Tahun 2000 – 2014.Jurnal Matematika UNAND. 4(1). 1-1.
Rahardi, Rustanto, dkk. 2003. Persamaan Diferensial Biasa, Jurusan Matematika, fakultas MIPA, Universitas Negeri Malang
Stephano MA dan Hyo. Jung Il. 2019. Estimation and Prediction of Population Using Mathematical Models in Tanzania. Journal of Mathematics (IOSR-JM). 15 (2) 73-82.
Susanta. 2008. Permodelan Matematis, Modul UT, Jakarta.
Tarumingkeng, R.C. 1994, Dinamika Populasi (Kajian Ekologi Kuantitatif), Pustaka Sinar Harapan, Jakarta
Ullah. MS,, Mustofa G, Jahan N & Khan MAH. 2019. Analyzing and Projection of Future Bangladesh Population Using Logistic Growth Model. International Journal of Modern Nonlinear Theory and Application. 8, 53-61.
Wei. H, Jiang. Y & Zhang. Y. 2015. A Review Of Two Population Growth Models And An Analysis Of Factors Affecting The Chinese Population Growth. Asian Journal of Economic Modelling. 3 (1). 8-20.
Zabadi AM, Assaf R, & Kanan M. 2017. A Mathematical and Statistical Approach for Predicting the Population Growth. World Wide Journal of Multidisciplinary Research and Development. 3(7). 50-59.
239
Discussion and feedback