EFFECT OF NON-UNIFORM HEAT SOURCE AND RADIATION ON UNSTEADY MHD FREE CONVECTION FLOW PAST AN INFINITE HEATED VERTICAL PLATE IN POROUS MEDIUM

E-Jurnal Matematika Vol. 9(4), November 2020, pp. 219-228

DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p302

ISSN: 2303-1751

EFFECT OF NON-UNIFORM HEAT SOURCE AND RADIATION ON UNSTEADY MHD FREE CONVECTION FLOW PAST AN INFINITE

HEATED VERTICAL PLATE IN POROUS MEDIUM

Pratibha Mishra^1§, Sweta Tripathi²

¹Department of Mathematics, Applied Sciences &Humanities, Kanpur Institute of Technology, Kanpur- 208002, U.P, India [E-mail: [email protected], [email protected]] ²Department of Electronics & Communication Engineering, Kanpur Institute of Technology, Kanpur- 208002, U.P, India [E-mail: [email protected]]

^§Corresponding Author

ABSTRACT

Influence of radiation and non-uniform heat source on unsteady, magneto-hydrodynamic free convection flow of viscous incompressible fluid past an infinite vertical heated plate embedded in porous medium of an optically thin environment with time dependent suction and viscous dissipation is investigated in this paper. Analytical solutions of the coupled non-linear equations are obtained for the velocity field and temperature distribution using oscillating time-dependent perturbation technique. Expressions for skin-friction and heat transfer rate are also derived. The effects of the material parameters on velocity, temperature, skin-friction, and rate of heat transfer are discussed quantitatively.

Keywords:  Non-Uniform heat source, time dependent suction, viscous dissipation

for an absorbing emitting liquid in the optically thick region and used the singular perturbation technique. Arpaci (1968) considered a similar problem in both, the optically thin and optically thick regions using the appropriate integral technique. Cheng and Ozisik (1972) investigated an absorbing, emitting and isotropically scattering fluid. Ali et. al. (1984) considered the effects of radiation on natural convective flow of a viscous fluid over a horizontal surface, while Bestman (1985) considered the same problem for the flow of non-Newtonian fluid along a vertical plate under uniform transverse magnetic field. Bestman & Adjepong (1988) also investigated free convection unsteady flow considering radiative heat transfer in a rotating fluid under the influence of uniform magnetic field. Ibrahim (1990) studied mixed convection and radiation interaction for flow of a viscous fluid considering horizontal and vertical surfaces, respectively. Hossain & Takhar (1996) studied the radiation effects on mixed convection along a vertical plate with uniform surface temperature and employed Keller Box finite

difference method. Hossain et. al. (2001) and Hossain et. al. (1999) extended this work for free convection and radiation interaction past a porous vertical plate in the presence of constant suction and with variable viscosity effects respectively. Azzam (2002) studied a similar problem for the effects of radiation on the flow and heat transfer past a moving vertical plate in the presence of magnetic field. Hydromagnetic flow showing the effects of radiation and heat transfer over a wedge was studied by Elbashbeshy and Dimian (2002) taking into account the variable viscosity. Cookey et. al. (2003) investigated the influence of viscous dissipation and radiation in unsteady MHD free convection flow past an infinite vertical heated plate in the optically thin environment with variable suction and used radiative heat flux in differential form.

The aim of the present investigation is to study the influence of radiation, variable suction and non-uniform heat source/sink on unsteady hydromagnetic free convection flow of a viscous fluid past a heated vertical porous plate taking into account the viscous dissipation. In the analysis, we considered both the space and the temperature dependent heat source/sink followed by Abo-Eldahab and El-Aziz (2004) and Abel et. al. (2007). Basu et. al. (2011) have studied Radiation and mass transfer effects on transient free convection flow of dissipative fluid past semi–infinite vertical plate with uniform heat and mass flux.

• 2. MATHEMATICAL FORMULATION

We consider the unsteady free convection flow of an incompressible viscous, electrically conducting, radiating fluid past an infinite porous heated vertical plate embedded in porous medium with time dependent suction and viscous dissipation. In Cartesian coordinate system the x'-axis is taken along the vertical porous plate in the upward direction and the z ' -axis normal to the plate. A constant magnetic field of strength B₀ is maintained in the z ' -direction and the plate moves uniformly along the positive x'-direction with velocityw'( t') . Initially, at time t '= 0 the plate is at the '

temperature T_∞ . At time t '> 0, the temperature

'

of the plate is suddenly increased to T_w and is maintained constant, which is highly enough to

initiate radiative heat transfer. Under Boussinesq’s approximation the flow is governed by the following equations:

∂w'

=0 . ∂z′

∂u' , τy + ^w O t

∂u' ∂z'

a¾√ a>√ ∂z'^{2 +} d t'

⅛ 1 (u '-w') +g β(T '-T))

i∖. J

(1)

^ul ⅛ ⁺

(2)

2

• ∂ T      '∂ T     K_τ Γ ∂ ²T 3  ’l      u f d u\ a

• —7 + W --7 — --- I--T--Q I + --- ( --7 )  +.

d t        dz     p C_p Ldz     dz ^tz!     p C_p ∂dz Jp C

(3)

^∂2q′′      2

---^z- - 3α²q ,-16ασr =

_∂z′2        z′∞ ∂

The boundary conditions relevant to the problem are

u′= w'(t ′) = w (1 + εe^{iω t}),

T′= T_w^'           at

'

u′→ 0,     T′ → T as

(5)

Since the medium is optically thin with relatively low density and α << 1 , the radiative heat flux given in equation (4) Cookey et. al. (2003) becomes

∂

q′ = 4α²(T′-T′ )

∂z ^z

∞

where α = δλ

0

Also from equation (1), it is obvious w ' is either a constant or function of time t ′ only. Hence, we assume

w ' = -w ' (1 + εe^{iω t})

such that ε << 1 and the negative sign indicates that the suction velocity is towards the plate.

In the energy equation (3) q′′′ is the space and temperature dependent internal heat generation/absorption (non-uniform heat

source/sinks), Abel et.al. (2007), which can be expressed in the simplest form as d' ' ' = ⅛ [^‘(^rw - ^r∞)(¹ + ^eeiω7') +

^v P^p

B *(T ^,-T'₀₀]]                             (8)

where A* and B* space and temperature dependent internal heat generation/absorption (non-uniform heat source/sinks).

non-dimensional

z=

We introduce following quantities and parameters

ω=

w'0z′	t=	w'02t′
ϑ,		ϑ,
ϑω′	w	w'
2,		=,
w'0		w0
T′-T′ ∞	1	ϑ2

^K=K′w'^2,

u′ u=

w₀

θ=       ,

′′

w∞

Gr =

ϑgβ(T_w′ - T_∞′)

R=

3

w'₀

4α²ϑ²

^,

^,

Ec =

µC

Pr = ^p

K_T

²

U₀

C_P(T_w′-T_∞′)

2 w'₀

M =M ²+K^-1.

M²

σ_eϑµ_e²H₀′²

2 ρw'₀

In view of (7) and above non-dimensional quantities and parameters, the Eqs. (2) and (3) transform to:

∂u           ∂u  ∂²u ∂w

- (1 + εe^iωt)   =    +   -M (u - w) + Grθ

∂t              ∂z   _∂z²   ∂t ¹

(9)

Pr - Pr(1 + re^iωt)^ = ζ⅛-Rθ +

at ^{v           j} ∂z ∂z²

^EcPr (⅛)² + [^χ *(1 + ^e e^lωt+B*θ]         (10)

Eqs. (9) and (10) are now subject to the boundary conditions.

u = w = 1 + εe^iωt  θ=1 at z = 0

^,

u →0 ,θ→0as    z →∞        (11)

(11), we use multiple parameters perturbation expansion of the form :

u(z, t) = u (z) +εu (z)e^iωt

θ ( z , t ) =θ ₀( z ) +εθ₁(z)e^iωt(12)

Introducing (12) in Eqs. (9)-(10) and neglecting the coefficients ofo(ε²) , we obtain:

u′′ + u′ -M u =-M -Grθ

θ′′+Prθ′ -Kθ =-EcPru′²-A*

u′′+ u′ -K u = -u′ -K -Grθ

θ′′+ Prθ′ -K θ =-Prθ′ -2EcPru′u′-A*

(16) where dashes denote differentiation with respect to z.

K =R -B*,     K =M +iω     and

K = K + iωPr

The boundary conditions (11), now transform to the following form:

u = 1, u = 1, θ=1, θ=0, at z = 0

u → 0,u → 0, θ →0, θ→0,asz →∞  (₁₇)

The Eqs. (13) – (16) are coupled equations and cannot be solved under boundary conditions (17). To solve these equations, we further assume that the viscous dissipation (Eckert number Ec) is small. Hence, to obtain the velocity and temperature field, we assume:

u₀(z) = u₀₀(z) + Ec u₀₁(z)

θ₀(z) = θ₀₀(z) + Ec θ₀₁(z)

u (z) =u  (z) +Ecu (z)

θ₁(z)=θ₁₀(z)+Ecθ₁₁(z)

Substituting (18) into Eqs. (13)-(16), we obtain:

3. METHOD OF SOLUTION

The Eqs. (9) and (10) are highly non-linear equations. Since ε is small (ε << 1), we can advance for analytical solution of these equations, subject to the boundary conditions

u₀′′₀ +u₀′₀ - M₁u₀₀ = -M₁ - Gr θ₀₀ (19) u′′ +u′ -M u = -Grθ (20 θ₀′′₀+Prθ′₀₀-K₁θ₀₀=-A* (21) θ′₀′₁ + Pr θ₀′ ₁ - K₁θ₀₁ = -Pru₀′₀ (22) u₁′′₀ + u₁′₀ - K₂u₁₀ = -u₀′₀ -K₂ - Gr θ₁₀ (23)

u′′ + u′ - K u = -u ′ - Grθ

θ₁′′₀+Prθ₁′₀-K₃θ₁₀=-Prθ₀′₀-A*(25)

θ₁′′₁+ Prθ ₁′₁-K₃θ ₁₁= -Pr θ₀′₁-2Pr u ₀′₀u₁′₀

The boundary conditions (17), transform to:

u₀₀ = 1, u₀₁

= 0, u₁₀ = 1, u₁₁ = 0, θ₀₀ =1,

θ=0, θ=0, θ=0 at z = 0

u ′  → 0, u ′ → 0, u ′ → 0, u ′→

θ′₀₀ →0, θ₀′ ₁ →0, θ₁′₀ →0, θ₁′₁ →0

As z →∞

(30)

The heat transfer rate ( Nu ) at the plate z = 0 is given by :

Nu=(^dθ )   +ε(^dθ ) eiωt

^{dz dz}

=Nu₁ +εNu₂e iωt

(31)

Where

Tl =-M₂(1-Pi - P2)-WlP₂ +

Ec [-M₂ ( P₆ ^- p? ^- Ps ^- P9)+WlP₆ ^-

₂ WlP₇-2M₂P₈-( ^l + M₂ ) P9].

Solving Eqs. (19) - (26) with boundary conditions (27) and substituting in (18) and using (12), the velocity and temperature distributions are given by:

θ(z, t) = θOO(z) +Εcθ01(z)+ ε[R1 (z, t) +

iS1 (z, t)]                                             (28)

u(z,t)=u00(z) +Ecu01(z) +ε[R2 (z, t) + iS2 (z, t)]                                             (29)

τ₂ =-m₄(1-Pu - Pi₂ - P13 - P14)-m₁P₁₁ ^{- m}₂Pι₂ ^{- m}3P13 ⁺ Ec [-M₄P₃₅ ^-2m1P₂3 -2^m₂P₂4 + ^m1P30 ^{- m}₂P31 + M₃P₃₂ ^- P3₆].

4. SKIN-FRICTION AND HEAT TRANSFER RATE

The skin-friction ( τ ) at the plate z = 0 is given by:

du ; )  +ε(^du i )eiωt

^{dz dz}

=τ₁ +ετ₂e iωt

Nu₁ =-m₁(1-A^∗ Ki ¹)+Ec [-m₁ ( ^p3 +

P4 + P₅)+2M₁P₃ +2m₂P₄+2(m₁ + m₂ ) P₆].

Nu₂ =   (Pi₀ +A^∗K3¹)-M₁P₁₀

+ Ec [-^m3P33 ^- MlPlS +2M₁P₁₆+2M2P17 + P34]

( Gr ), Eckert number ( Ec ), space dependent

*

heat source/sink ( A ) and temperature

*

dependent heat source/sink ( B ). To be realistic, the values of Prandtl number ( Pr ) are chosen at one atmospheric pressure for air ( Pr = 0.71), electrolyte solution (Pr = 1.0), water at 100⁰C (Pr = 1.78) and water at 60⁰C ( Pr = 3.0). All numerical calculations are carried out for the fixed values of n = 0.5, t =

1.0 and ε = 0.01. The values of frequency parameter (ω), time (t) and perturbation parameter (ε) are fixed and non-zero; in all the cases, a convective flow regime in presence of variable suction velocity is considered. The values of the remaining parameters are chosen arbitrarily but do retain physical significance in real energy system applications [5]. The values of the space dependent heat source/sink *

parameter ( A ) and temperature dependent *

heat source / sink parameter ( B ) are chosen following Abel et. al. (2007). We now proceed with the discussion and results.

Fig.-1 depicts variations in the velocity field versus z for different numerical values of

Prandtl number ( Pr ) and magnetic parameter (M) at the fixed values of R = 2.0, K = 10.0,

Gr = 14.0, Ec = 0.01, A= 0.3 and *

B = 0.3. It is observed that the velocity increases near the plate and after attaining a maximum value it decreases asymptotically to horizontal axis. As expected, we observe a decrease in the velocity field as the Prandtl number ( Pr ) increases. In fact, increase in Prandtl number ( Pr ) decreases the temperature buoyancy effect which also leads to a decrease in the velocity boundary layer. This observation is in good agreement with in Mbeledogu and Ogulu (2007). It is also observed that an increase in magnetic parameter ( M ) results in a decrease in the velocity field consistent with many other studies.

Hence, hydromagnetic drag embodied in Eq. (9) retards the transient velocity. This is an important controlling mechanism in nuclear energy systems heat transfer, where momentum development can be reduced, for oscillatory

flow regimes, by enhancing the magnetic field

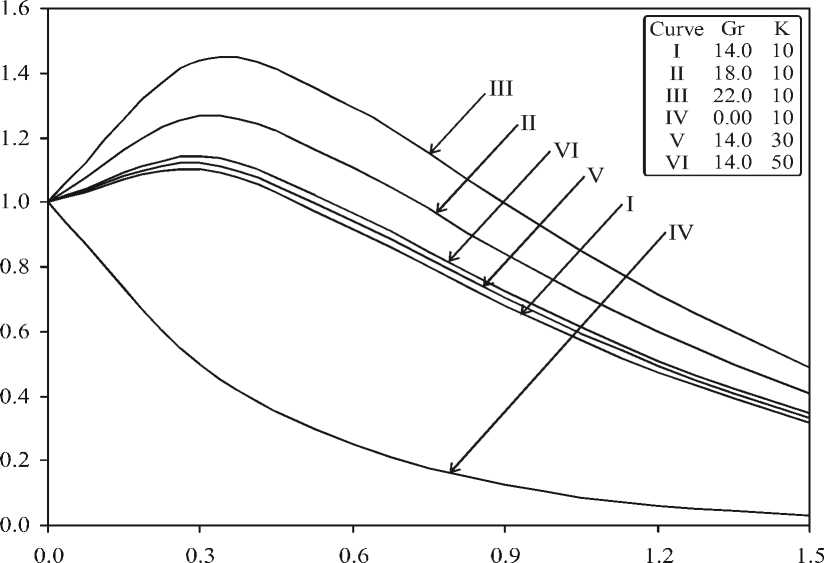
Fig.-2 illustrates the effect of free convection parameter ( Gr) and permeability parameter ( K ) on velocity field versus z for fixed values of Prandtl number ( Pr ) and magnetic parameter (M) at the fixed values of R = 2.0, M = 1.0, K = 10.0, Pr = 0.71,

Ec = 0.01, A = 0.3 and B = 0.3. We observe that velocity increases with increase in free convection parameter (Gr), i.e., maximum velocity corresponds to maximum free convection parameter (Gr > 0). Hence, buoyancy parameter ( Gr ) has dominant effect in escalating transient velocity [25]. Also, we note that transient velocity increases with increase in permeability parameter ( K ). As expected, as K increases, the bulk porous medium is lowered, which increases the momentum development of the flow regime, thereby enhancing transient velocity (Basu, at al. (2011). It is interesting to note that in absence of buoyancy parameter, i.e., Gr = 0.0 the velocity decreases drastically but asymptotically as y increases. These observations are in good agreement of Mbeledogu and Ogulu (2007).

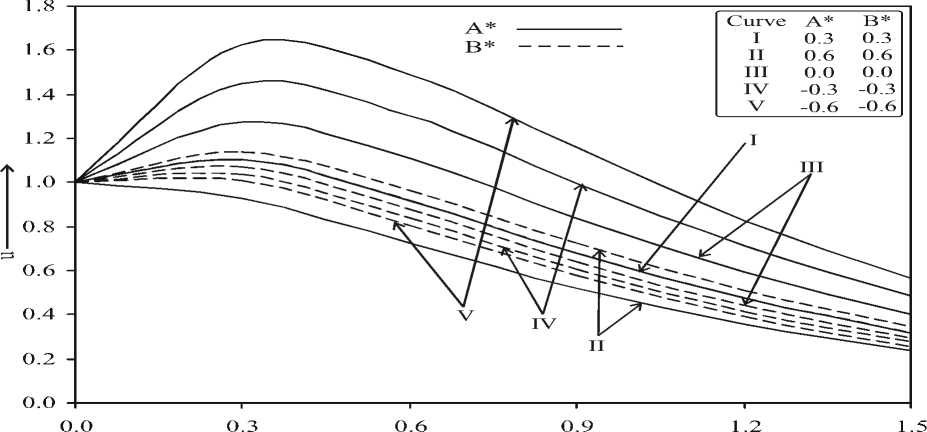
Fig.-3 shows the variation in the velocity field with respect to z for different numerical values of space dependent heat source/sink ( A^*) and temperature dependent heat source/sink _*

(B ) at the fixed values for R = 2.0, M = 1.0 , Pr = 0.71, Ec = 0.01, Gr = 14.0 and

**

K = 10.0, where A > 0 and B > 0 corresponds to internal heat generation, i.e. heat **

source while A < 0 and B < 0 correspond to internal heat absorption, i.e., heat sink.

uu

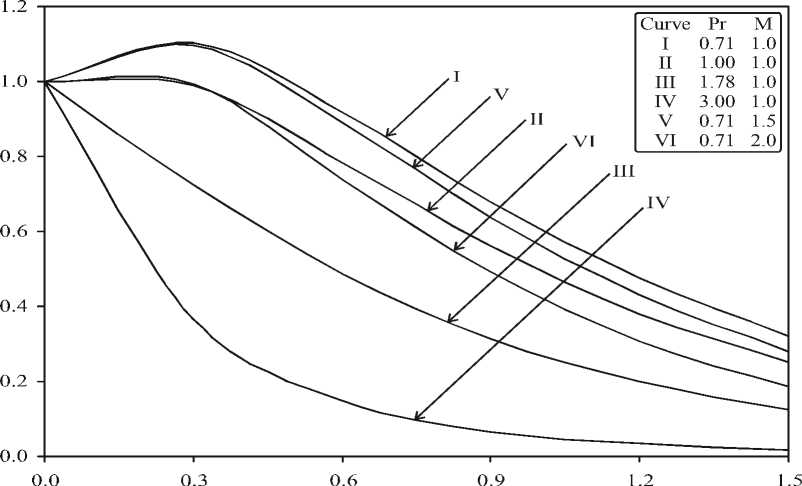
Fig-1: Effect of Pr and M on velocity field at K = 10.0, Gr = 14.0, Ec = 0.01, R = 2.0, A* = 0.3 and B* = 0.3

z---------->

Fig-2: Effect of Gr and K on velocity field at M = 1.0, Pr = 0.71, Ec = 0.01, R = 2.0, A* = 0.3 and B* = 0.3

z---------->

Fig-3: Effect of A* and B* on velocity field at K = 10.0, M = 1.0, Gr = 14.0, Pr = 0.71, Ec = 0.01 and R = 2.0

z---------->

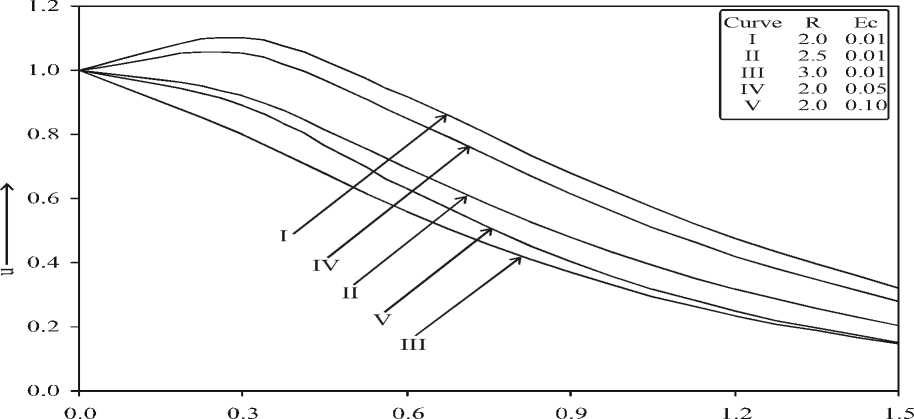
Fig-4: Effect of R and Ec on velocity field at K = 10.0, Gr = 14.0, Pr = 0.71, M = 1.0, A* = 0.3 and B* = 0.3

Curve	Pr	M
I	0.71	1.0
II	1.00	1.0
III	1.78	1.0
IV	3.00	1.0
V	0.71	1.5
VI	0.71	2.0

z

Fig-5: Effect of Pr and M on temperature field at K = 10.0, Gr = 14.0, Ec = 0.01, R = 2.0, A* = 0.3 and B* = 0.3

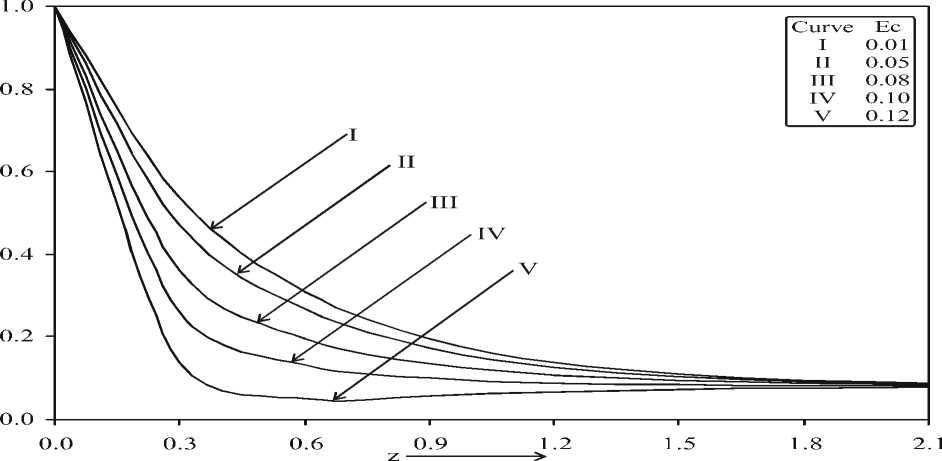
Fig-6: Effect of Ec on temperature field at K = 10.0, R = 2.0, Gr = 14.0, Pr = 0.71, M = 1.0, A* = 0.3 and B* = 0.3

It is noted that an increase in space *

dependent heat source (A > 0) and

*

temperature dependent heat source (B > 0) parameters decreases the velocity field while an *

increase in space dependent heat sink (A < 0)

*

and temperature dependent heat sink ( B < 0 ) parameters enhances the velocity field. The curve III shows the variation in the velocity field in absence of non-uniform heat source or sink. These results are in good agreement with those of Abel et. al. (2007). Fig.-4 demonstrates the variations in the dimensionless velocity field versus z for different numerical values of

radiation parameter ( R ) and Eckert number (Ec) at the fixed values of Pr = 0.71,

K = 10.0, Gr = 14.0, M = 1.0, A = 0.3 *

and B = 0.3 . It is observed that an increase in radiation parameter or Eckert number decreases the velocity and velocity boundary layer. These results are in excellent agreement with Cogley et. al (1968).

Fig.-5 expresses the variations in temperature field versus z for different numerical values of Prandtl number ( Pr ) and magnetic parameter (M) at the fixed values of R = 2.0, K = 10.0, Gr = 14.0, Ec = 0.01, **

A = 0.3 and B = 0.3 . It is observed that a decrease in temperature and temperature

boundary layer exists with increase in Prandtl number and magnetic parameter. It is clear from the curve that the temperature of water at 60⁰C is more stable in comparison to water at 100⁰C

Fig.-6 indicates the effect of Eckert number ( Ec ) on temperature field versus z for fixed values R = 2.0, M = 1.0, K = 10.0,

_*

Pr = 0.71, Gr = 14.0, A = 0.3 and

B = 0.3 . It is clear that the temperature of the fluid uniformly decreases as Eckert number

increases.

The variation in the space dependent heat *

source/sink ( A ) parameter on temperature distribution versus z at R = 2.0, M = 1.0, K = 10.0,      Pr = 0.71,      Ec = 0.01,

_*

Gr = 14.0 and B = 0.3 . For A > 0

corresponds to internal heat generation, i.e. heat *

source while A < 0 correspond to internal heat absorption, i.e., heat sink. It is noted that an increase in space dependent heat source *

(A > 0) parameter increases the temperature and temperature boundary layer while reverse effect is noted for an increase in space *

dependent heat sink (A < 0) parameter. The curve III shows the variation in the temperature field in absence of non-uniform space *

dependent heat source or sink. In fact A > 0

implies that the thermal boundary layer generates the energy, which causes the temperature of the fluid to increase with *

increase in ^  > 0 (heat source) whereas for

*

A < 0 (heat absorption) the temperature

*

decrease with increase in the value of A < 0.

REFERENCE

Abel, M.S.,        Siddheshwar, P.G.,

Nandeppanavar, M.M. 2007. Heat transfer in a viscoelastic boundry layer flow over a stretching sheet with viscous dissipation and non-uniform heat source. Int. J.Heat Mass Traner, 50, 960-966.

Abo-Eldahab, E.M., El-Aziz, M.A. 2004. Blow /suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/ absorption. Int J. Thermal Sci., 43, 709-719.

Ali,M.M., Chen, T.S., Armali, B.F. 1984. Natural convection radiation interaction in boundary layer flow over horizontal surface. AIAAJ, 22, 1797-1803.

Arpaci, V.S. 1968. Effect of thermal radiation on the laminar free convection from a , heated vertical plate. Int. J. Heat Mass Transfer , 11, 871-881.

Ashely, A. 1995. Electric rockets gets a boost. Mech. Energy, 4, 61-65.

Azzam, G.E.A. 2002. Radiation effects on the MHD free mixed convective flow past a semi-infinite moving vertical plate for high temperature difference. Phys. Scripta, 66, 71-76.

Basu, B., Prasad, V.R., Reddy, N.B. 2011. Radiation and mass transfer effects on transient free convection flow of dissipative fluid past semi –infinite vertical plate with uniform heat and mass flux. JAFM,4(1), 15-26.

Beg, O.A., Takhar, H.S., Ajay Kumar Singh. 2005. Multiparameter perturbation analysis of unsteady oscillatory magnetoconvection in porous media with heat source effects. Int. J. Fluid Mech. Research, 32, 635-661.

Bestman, A.R., Adjepong, S.K. 1988. Unsteady hydromagnetic , free convection flow with

radiative heat transfer in a rotating fluid, Astrophysics Space Sci., 143, 73-80.

Bestman, A.R. 1985. Free convection heat transfer to steady radiating non -Newtonian MHD flow past a vertical porous plates, Int. J.Numer . Method. Engng., 21, 899908.

Brewster, M.Q. 1992. Thermal Radiative Tranfer Properties. New York: John Wiley & sons. Inc.

Cess, R.D. 1966. The interaction of thermal radiation with free convection heat transfer, Int. J. Heat Mass Transfer, 9, 1269-1277.

Chengs, E.H., Ozisik, M.N. 1972. Radiation with free convection in an absorbing, emitting and scattering medium, Int. J. Heat Mass Transfer, 15, 1243-1252.

Cogley, A.C., Vincenti, W.C., Gilles, S.E. 1968. Differential approximation for radiative transfer in a non-gray gas near equilibrium. Am. Inst. Aeronaut. Astronau. J., 6, 551-555.

Cookey, C.I., Ogulu, A., Pepple, V.B.O. 2003. Influence of viscous dissipation and radiation   on  unsteady MHD free

convection flow past an infinite heated vertical plate in a porous medium with time dependent suction. Int. J. Heat Mass Transfer, 46, 2305-2311.

Cowling,     T.G.     1957.     Mangneto-

hydrodynamics. New York: Inter Science Publication, Inc

Elbashbeshy, E.M.A., Dimian, M.F. 2002. Effect of radiation on the flow and heat transfer over a wedge with variable viscosity. Appl. Math. Comput., 132, 445454.

Ferraro, V.C.A. and Plumpton, C. 1961. An Introduction to Magneto-Fluid Mechanics. London: Oxford Uni. Press.

Hossain, M.A., Takhar, H.S. 1996. Radiation effect on mixed convection along a vertical plate with uniform surface temprerature. Heat and Mass Transfer, 31, 243-248.

Hossain, M.A., K. Khanafer, K. Vafai. 2001. The effect of radiation on free convection of Fluid with variable viscosity from a porous vertical plate, Int. J. Thermal Sci., 40, 115-125.

Hossain, M.A., Alim, M.A., Ress, D. 1999. The effect of radiation on free convection from porous vertical plate,  Int. J. Heat

Mass Transfer, 42, 181-191.

Ibrahim, F.S. 1990. Mixed convection radiation interaction in boundary layer flow over horizontal surfaces, Astrophysics Space Sci.,168, 263-276.

Mbeledogu, I.U., A. Ogulu, A. 2007. Heat and mass transfer of an unsteady MHD natural convection flow of a rotating fluid past a vertical porous flat plate in the presence of radiative heat transfer. Int. J. Heat Mass Transfer, 50, 1902-1908.

228