A KONTROL OPTIMAL PADA MODEL DINAMIK PENYEBARAN VIRUS KOMPUTER DENGAN MENGGUNAKAN PONTRYAGIN MAXIMUM PRINCIPLE (PMP)

E-Jurnal Matematika Vol. 9(4), November 2020, pp. 278-282

DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p309

ISSN: 2303-1751

KONTROL OPTIMAL PADA MODEL DINAMIK PENYEBARAN VIRUS KOMPUTER DENGAN MENGGUNAKAN PONTRYAGIN MAXIMUM PRINCIPLE (PMP)

Asmianto^1§, Kridha Pusadwijayanti², Mochammad Hafiizh³

¹Program Studi Matematika FMIPA-Universitas Negeri Malang [Email: [email protected]]

²Program Studi Matematika FMIPA-Universitas Negeri Malang [Email: [email protected]] ³Program Studi Matematika FMIPA-Universitas Negeri Malang [Email: [email protected]]

^§Corresponding Author

ABSTRACT

In this paper, it is discussed about giving control variable to dynamic systems to process the spread of viruses on computers. The dynamic model describes the process of spreading viruses on the computer, where susceptible can be instantly removed and infected can instantly become susceptible. And through qualitative analysis on the model is given a control and completed using the Pontryagin Maximum Principle (PMP) method on infected interactions so that the infected computer can be minimized. Dynamic models that have been given control are simulated using MATLAB software and the results show the infected computer is reduced significantly.

Keywords:Optimal control, Pontryagin Maximum Principle, SIR model, Mathematical model.

• 1.    PENDAHULUAN

Internet merupakan salah satu alat yang sangat berguna bagi seseorang untuk berkomunikasi, mencari informasi, membeli barang ataupun pelayanan lain. Dengan adanya internet banyak sekali kegiatan manusia yang menjadi lebih mudah untuk dikerjakan. Apalagi saat ini merupakan masa pandemi karena adanya covid - 19, hampir semua pembelajaran di indonesia menggunakan daring atau online dan tentunya itu semua membutuhkan internet. Orang bekerja pun banyak yang masih WFH (Work From Home). Jika kita bicara mengenai internet maka sangatlah erat hubungannya dengan komputer atau laptop. Seseorang yang biasanya bekerja menggunakan komputer atau laptop tentu tidak asing lagi dengan yang namanya virus. Virus merupakan salah satu ancaman yang cukup mematikan bagi komputer. Penggunaan sistem jaringan pada komputer, menyebabkan virus komputer dapat menyebar dari komputer satu ke komputer lain yang saling terhubung. Komputer yang sudah terjangkit oleh virus tidak akan bisa bekerja secara optimal karena semakin lama virus tersebut dalam komputer dapat menyebabkan kerusakan pada software maupun hardware. Oleh karena itu perlu adanya suatu kontrol

untuk mencegah atau meminimalisir penyebaran virus pada komputer. Pada paper ini digunakan metode Pontryagin Maximum principle, diharapkan dengan adanya suatu pengontrol, komputer lebih aman dan bisa digunakan secara optimal, baik untuk bekerja, bermain ataupun keperluan lain.

• 2.    METODE PENELITIAN

Dalam paper ini, diusulkan tipe model SIR (Susceptible-Infected-Removed) dalam model dinamik penyebaran virus komputer dengan intervensi manusia. Total komputer yang diteliti N(t) dibagi menjadi 3 kategori atau kelompok diantaranya: susceptible yaitu komputer yang bebas dari virus namun rentan terhadap serangan virus S(t), infected yaitu komputer yang terinfeksi adanya virus ((t), dan removed R(t) yaitu komputer yang sehat atau normal dan mempunyai proteksi terhadap virus pada waktu t, untuk t ≥ 0. konstruksi model matematika berdasarkan asumsi-asumsi berikut : (Chenquan et all 2002).

• (1)    Semua akses komputer awalnya bebas dari virus, namun seiring berjalannya waktu ada

yang berubah dan prosentase peningkatan Susceptible sebesar δ.

• (2)    Setiap saat internal komputer terputus dengan internet dengan kemungkinan sebesar δ.

• (3)    Karena pengaruh komputer yang sudah terinfeksi sebelumnya, maka setiap saat prosentase komputer yang terinfeksi meningkat sebesar βS(t)I(t), dimana β konstanta positif

• (4)    Karena adanya faktor perawatan maka komputer yang terinfeksi I(t) dapat menjadi komputer yang sehat/normal R(t) dengan probabilitas sebesar /i atau menjadi Susceptible S(t)  dengan kemungkinan

sebesar /2 .

• (5)    Karena kehilangan proteksi, maka setiap saat komputer dalam kategori recovered bisa menjadi susceptible dengan kemungkinan sebesar «2 .

• (6)    Karena adanya suatu proteksi atau kontrol terhadap komputer maka setiap saat komputer dengan kategori Susceptible bisa pulih menjadi recovered dengan kemungkinan sebesar :

Jika asumsi 1 sampai dengan 6 dinyatakan dalam bentuk diagram kompartemen maka didapatkan sebagai berikut:

• 1.    Membentuk fungsi    pontryagin

(hamiltonian): H(x,U,λ,t)=

g(X,U,t)+Xf(X,λ,t).

• 2.    Memaksimalkan H(X,U,λ,t) terhadap semua vektor kontrol untuk mendapatkan U∗=U ∗( X,λ,t).

• 3.    Mendapatkan fungsi pontryagin

_∗               TTlClX r i

H ∗₍x,λ,t)=Ug U^H (x,U,λ,t).

• 4.    Menyelesaikan persamaan state dan costate, dengan kondisi batas yang diberikan.

• 5.  Mensubstitusikan hasil pada langkah 4

ke ekspresi U^∗ untuk mendapatkan kontrol optimal.

• 3.    HASIL DAN PEMBAHASAN

Dalam hal ini, diusulkan dan dianalisis masalah kontrol optimal yang diaplikasikan ke model dinamik penyebaran anti virus yang dideskripsikan oleh model (1). Dengan menambahkan suatu kontrol U(t) pada sistem (1) yang merepresentasikan adanya treatment pada individu infected melalui software anti virus, dimana interval U adalah 0≤U≤1. Model matematika dilengkapi suatu kontrol diberikan oleh sistem persamaan differensial biasa tak linear berikut:

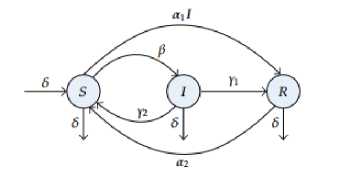
Gambar 1. Diagram Kompartemen model SIRS

' i̇( )= δ- a₁S( ) ( )- SS ( )

⁺ Y₂I( ) -u( ) βS ( ) ( ) + a₂R( );

• 1    (̇ )= u( ) βS ( ) ( )- Y₂I( ^)-  (2)

δl ( ) - YiI( _);           (2)

⎪   İ ( )= YiI( )+ a₁S ( ) ( )-

⎩         δR ( ) - U₂R ( );

Dan dengan asumsi-asumsi tersebut didapatkan model dinamik sebagai berikut: (Chenquan et all 2002).

̇(t)= δ- a₁S(t)I(t)- δS (t)+

Y₂I(t) - βs (t)I(t) + U₂R(t);        (1)

i̇(t)= βS (t)I(t)- Y₂I(t)- δl (t)-

Y1I(t);

l̇ (t)= YiI(t)+ a₁S(t)I(t)- δR (t) - a₂R(t);

Pontryagin Maximum Principle (PMP) adalah salah satu metode yang cukup popular digunakan para peneliti untuk menyelesaikan masalah kontrol optimal. Secara umum langkah-langkah penyelesaian masalah kontrol optimal menggunakan metode Pontryagin Maximum Principle (PMP) adalah sebagai berikut: (Subiono, 2013)

Dengan kondisi awal S(0) ≥0,I(0)≥0 dan R(0) ≥0.

Tujuan akhir dari masalah kontrol optimal dari model penyebaran virus komputer adalah untuk mendapatkan bentuk yang optimal sehingga dapat mengoptimalkan fungsi objektif dengan kontrol U(t) sebagai proteksi yang dilakukan pada komputer agar terhindar atau meminimalisir penyebaran virus komputer.

J(U₁, U_{2)=∫ (}I(t)+C₁U² (t)) dt (3) dengan, ^cι _{= ,} ^cι adalah konstanta positif.

Pada penyelesaian kontrol optimal ini akan dibahas langkah -langkah penyelesaian kontrol optimal tentang penyelesaian menggunakan kontrol optimal untuk mendapatkan treatment yang optimal dengan fungsi tujuan pada

persamaan (3). Dengan kendala pada sistem (2). Berikut Langkah - langkah penyelesaian kontrol optimal menggunakan metode Pontryagin Maximum Principle (PMP).

• 1.    Menentukan fungsi Hamiltonian

  • — —λl (—l₁i*()) — δ

  -uKt)βS*(t)I*(t))

  -λ2 u*(t)β i*(t)

  • ^{- λ}₃aιi*(t)

  
  

M = I (t') + l₁u ²())

+ λ_l(δ - a_l S(t)I(t)- δS(t)

+ γ2K) - u(t)βS(tII(t)

+ a ₂R(t))

+ λ2(u(t)βS(t)I(t)- γ2KO

• -    δi(t)- γlI(t))+λ₃(γli( t)

  2.

  
  

+ a_lS(t)I(t) - δR(t)

• -    a2R(t)

Memaksimumkan fungsi hamiltonian terhadap semua vektor u (t) atau biasa disebut dengan kondisi stasioner.

∂ M

=0

c₁u*(t) - λ_lβS(t)I(t)

+ λ2 βS(t)I(O

= 0

Sehingga diperoleh,

U *(t)

(λlβS(t)I(t)-λ2 βs(t)i(θ)

λ2 (t) —

∂M* ~∂F

• — —1 — λl(—λlS*(t) + γ2 — u*(t)βS*(t) -λ2(u*(t)βS*(t)-γ2 ^{- δ -γ}l) ^{- λ}3(^γl + αlS*(t)))

• 5. Penyelesaian dengan forward-backward sweep Runge Kutta orde 4

Penyelesaian numerik untuk mengoptimalkan sistem dalam permasalahan ini diselesaikan menggunakan software MATLAB dengan nilai parameter hipotesis yang realistis dan kondisi awal yang diberikan sebagai berikut : β — 0.3, δ — 0.01, a_l — 0.2, a₂ — 0.15, γ_l — 0.1, γ₂ — 0.2, S(0) — 0.5, I(0) — 0.4 (Chenquan et al., 2002).

3.

4.

Cl

Karena      u_l(t) himpunan tertutup

[0,1], maka,

u* (t) = min {max {

_o βS(t)I(t)(λl -

Cl

Menyelesaikan Persamaan State

∂H *

⁴ⁱ )■')

S*(t) =

U Ai

= S- a_lS*(t)I*(t) - δS*(t) + γ₂I*(t)

-u*(t)βS*(t)I*(t)

+ a2R*(t)

∂H *

— U*(t)βS*(t)i*(t) - γ2i*(t) - δI*(t)

-γlK(t)

∂H *

^s∙^ffl=¾

= γ_lI*(O + a_lS*(t)I*(t) - δR*(t)

^{- a}2^R*^(t)

Menyelesaikan Persamaan Co-State

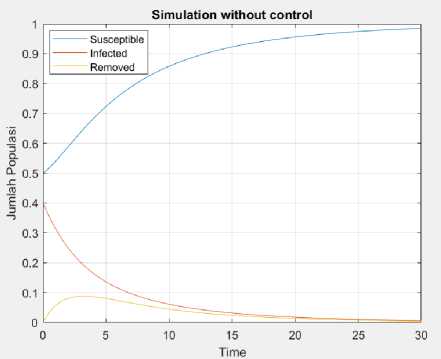
Gambar 2. Plot penyebaran virus komputer sebelum di berikan kontrol.

. *_    UM*

^{λl (n}      US*

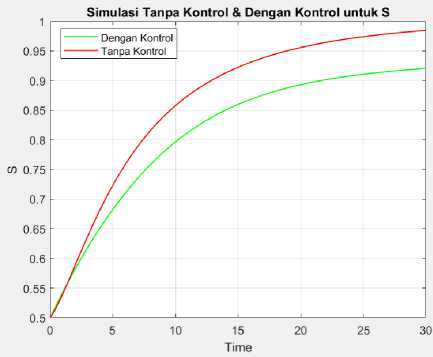
Gambar 3. Plot dari komputer yang rentan terhadap virus S(t) dengan kontrol dan tanpa control

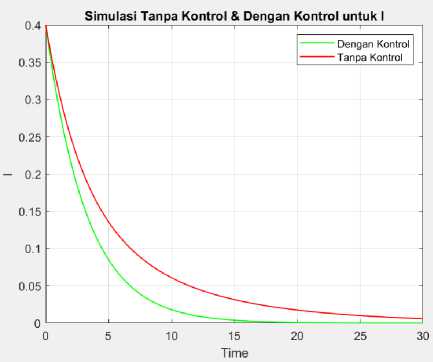
Gambar 4. Plot dari komputer yang terinfeksi oleh virus komputer I(t) dengan kontrol dan tanpa kontrol.

Gambar 5. Plot dari komputer yang sehat dan mempunyai proteksi terhadap virus R(t) dengan kontrol dan tanpa kontrol

Pada Gambar 2, ditunjukkan simulasi penyebaran virus komputer pada setiap kategori S(t),I(t') dan R)). Sedangkan pada gambar 3, gambar 4 dan gambar 5 ditunjukkan simulasi perbandingan penyebaran virus komputer pada masing-masing kategori sebelum dan sesudah dikontrol. Garis merah menunjukkan penyebaran virus komputer sebelum diberikan kontrol dan garis hijau menunjukkan jumlah penyebaran virus komputer setelah diberikan suatu kontrol. Dari gambar 3 dapat dilihat bahwa penyebaran virus komputer setelah diberikan suatu kontrol membuat jumlah komputer yang rentan terhadap virus berkurang cukup drastis. Gambar 4 menujukkan bahwa pemberian suatu kontrol u(t’) pada interaksi antara komputer yang rentan dan komputer yang terinfeksi cukup efektif, hal ini dapat dilihat bahwa jumlah komputer yang terinfeksi virus komputer juga berkurang cukup drastis. sedangkan pada gambar 5 dapat dilihat bahwa jumlah komputer yang sehat dan mempunyai proteksi terhadap virus komputer bertambah cukup pesat. Hal ini dikarenakan komputer yang awalnya terinfeksi dan rentan terhadap virus setelah diberikan suatu kontrol menjadi komputer yang sehat dan lebih aman terhadap adanya virus dari pada sebelum-sebelumnya. Hal ini menunjukkan bahwa pemberian kontrol pada interaksi antara komputer yang terinfeksi virus dan komputer rentan terhadap virus serta metode Pontryagin Maximum Principle (PMP) cukup efektif untuk diterapkan.

4. KESIMPULAN DAN SARAN

Dalam penelitian ini, dilakukan suatu kontrol optimal terhadap model epidemi SIR penyebaran virus komputer menggunakan metode Pontryagin Maximum Principle (PMP). Penyebaran virus komputer sebelum dan sesudah dikontrol disimulasikan menggunakan software MATLAB agar bisa dilihat secara langsung perbandingan dan hasil dari pemberian kontrol pada model tersebut. Dari simulasi numerik dapat dilihat secara jelas bahwa terjadi perubahan yang cukup significan antara jumlah penyebaran virus komputer sebelum dan sesudah di kontrol. Setelah dilakukan suatu kontrol jumlah penyebaran virus komputer yang rentan dan terinfeksi virus berkurang cukup drastis, sedangkan hasil dari simulasi kategori R ecovered atau komputer

yang sehat dan mempunyai proteksi terhadap virus bertambah cukup pesat dengan seiring berjalannya waktu. Hal ini menunjukkan bahwa Pemberian suatu kontrol pada interaksi komputer yang rentan dan terinfeksi virus cukup efektif untuk diterapkan. Dengan demikian komputer akan lebih terlindungi dan aman dari virus komputer.

DAFTAR PUSTAKA

Chenquan Gan, Xiaofan Yang et al, 2002.

Propagation of computer virus under Human Intervention: A dynamical Model

Subiono. 2013. Sistem Linear dan kontrol Optimal. Surabaya: Matematika ITS.

Binay Kumar Mishra,Mathematical Model on Attack of Worm and Virus

in Computer Network,Vol. 9, No. 6 (2016), pp. 245-254.

Mei Peng, Huajian Mou,A Novel Computer Virus Model and Its Stability, VOL. 9, No. 2, February (2014).

Prasant Kumar Nayak, Debdas Mishra and Subhashree Ram,e Epidemic Model on the Computer Viruses in the Network,2015, 2(9): 78-82.

SM Omair and Samir Kumar Pandey,e Epidemic Model on the Computer Viruses in the Network,2015, 2(9): 78-82

N Ilmayasinta, EA Irhami. 2019. Optimal control for extraction lipid model of microalgae Chlorella Vulgaris using PMP method. Journal of Physics: Conference Series 1218 (1), 012043.

282