ANALISIS KESTABILAN MODEL MATEMATIKA JUMLAH PEROKOK PENGARUH KENAIKAN HARGA ROKOK DENGAN DINAMIKA AKAR KUADRAT
on
E-Jurnal Matematika Vol. 9(4), November 2020, pp. 283-287
DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p310
ISSN: 2303-1751
ANALISIS KESTABILAN MODEL MATEMATIKA JUMLAH PEROKOK PENGARUH KENAIKAN HARGA ROKOK DENGAN DINAMIKA AKAR KUADRAT
Fidelis Nofertinus Zai1§, Aryl Zuldaus Sembiring2, Ardinal Vanbasten3, Anggi Novita Nasution4, Lasker Pangarapan Sinaga5
1Jurusan Matematika UNIMED [Email: fidelisnofertinus@gmail.com] 2Jurusan Matematika UNIMED [Email: arylkembaren98@gmail.com] 3Jurusan Matematika UNIMED [Email: ardinalbutarbutar@gmail.com] 4Jurusan Matematika UNIMED [Email: angginst06@gmail.com] 5Jurusan Matematika UNIMED [Email: lazer_integral@yahoo.com]
§Corresponding Author
ABSTRACT
Consumption of cigarettes in large quantities by the public is one of the main concerns in every country because cigarettes contain harmful ingredients that can trigger various diseases. This journal will explain the mathematical model of the number of smokers affected by rising prices of cigarettes with square root dynamics. The population is divided into four, composed of potential smokers, occasionally smokers, heavy smokers, and ex-smokers. The results of the model analysis are that there is a single point of smoker’s endemic equilibrium. If conditions are met, then the endemic equilibrium point of smokers will be asymptotically stable, and over a long period of time there will always be a spread of smokers.
Keywords: Asymptotically Stable, Equilibrium State, Mathematical Model the Number of Smokers
individu yang rentan menjadi perokok, Kelas D: kelompok individu perokok aktif dan Kelas R: kelompok individu yang telah berhenti merokok. Model tersebut dikembangkan oleh Sharomi, dkk. (2008), Alkhudhari, dkk. (2014), mengkaji sistem dinamika model matematika pencegahan pertambahan perokok dengan mengelompokkan populasi menjadi empat kelompok, yaitu P(t): Kelompok individu yang potensial menjadi perokok, S(t): Kelompok individu yang merokok aktif, Qt(t): Kelompok individu perokok temporer, dan Qp(t): Kelompok individu yang permanen berhenti merokok. Jami, dkk (2013) dalam jurnal yang berjudul “Model Matematika Pertambahan Jumlah Perokok dengan Penerapan Denda” mengelompokkan populasi dalam tiga kelas yaitu: P (Potensial Perokok), S (Individu Perokok) dan Q (Populasi Berhenti Merokok).
M.V. Anggraini, dkk. (2013) dalam jurnalnya yang berjudul “Analisis Model Matematika Jumlah Perokok dengan Dinamika Akar Kuadrat”. Jurnal tersebut melakukan
pengembangan model matematika Zeb dkk, pengembangan dilakukan pada bentuk alur model. Soleh & Sazmita (2017) mengkaji model matematika jumlah perokok dengan dinamika akar kuadrat dan faktor migrasi. Berdasarkan latar belakang di atas akan dilakukan analisis model matematika dengan dinamika akar kuadrat dengan adanya pengaruh kenaikan harga rokok.
Tujuan dilakukan penelitian ini adalah untuk mengetahui bentuk kesetimbangan model matematika pengaruh kenaikan harga rokok dengan dinamika akar kuadrat dan perilaku populasi perokok melalui simulasi numerik.
Model yang digunakan dalam penelitian ini adalah:
dP = φ - β PLl - (d + μ + h) P dt
dL = βPll - (γ+d + μ + h)L dt
dS = γL - (δ + d + μ + h)S
dt
dQ = (δ + h)S + hL - (μ + d)Q dt
model di atas merupakan pengembangan dari model Zeb, dkk (2015).
Penelitian dengan cara studi literature dilakukan dengan tahapan sebagai berikut:
-
1. Menentukan asumsi-asumsi yang
digunakan pada model matematika jumlah perokok pengaruh kenaikan harga rokok dengan dinamika akar kuadrat.
-
2. Menentukan titik kesetimbangan dari model
-
3. Menganalisis kestabilan titik
kesetimbangan yang telah didapat dengan linierisasi dan menentukan Matriks Jacobian.
-
4. Menentukkan jenis kesetabilan dengan kriteria Routh-Hurwitz.
-
5. Membentuk simulasi numerik
menggunakan aplikasi MATLAB.
-
6. Menarik kesimpulan.
Tabel 1. Identifikasi parameter dan variabel dalam model
|
No |
Parameter dan Variabel |
Keterangan |
|
1. |
P |
Perokok potensial |
|
2. |
L |
Perokok kadang-kadang |
|
3. |
S |
Perokok berat |
|
4. |
Q |
Mantan perokok |
|
5. |
φ |
Jumlah individu pada populasi |
|
6. |
β4PL |
Laju kontak dinamika akar kuadrat antara perokok potensian dengan perokok kadang-kadang |
|
7. |
d |
Laju kematian disebabkan oleh rokok |
|
8. |
μ |
Laju kemarian alami |
|
9. |
γ |
Laju berkurangnya perokok kadang-kadang |
|
10. |
δ |
Laju berhenti merokok |
|
11. |
h |
Laju kenaikan harga rokok |
Model matematika jumlah perokok dengan dinamika akar kuadrat dan faktor migrasi ini membutuhkan beberapa asumsi yang sesuai dan berhubungan dengan model yang akan diperoleh. Adapun asumsi-asumsi yang digunakan pada model matematika ini adalah sebagai berikut:
-
1. Populasi bersifat terbuka
-
2. Adanya proses kelahiran dan kematian
alami dalam populasi jumlah perokok dengan laju kelahiran dan kematian konstan.
-
3. Individu yang potensial perokok akan
menjadi seorang perokok, disebabkan karena adanya interaksi dengan perokok kadang-kadang, sedangkan individu perokok kadang-kadang akan menjadi seorang perokok berat apabila terjadinya interaksi secara intens antara keduanya.
-
4. Individu yang sudah berhenti merokok
tidak akan merokok lagi.
-
5. Selalu terdapat interaksi antara perokok
potensial dan perokok kadang-kadang, yaitu PfL ≠ 0 sehingga P ≠ 0 dan L ≠ 0.
-
6. Setiap populasi jumlah perokok masing-
masing mengalami laju kematian alami konstan dengan μ > 0, laju kematian karena rokok dengan d > 0 dan juga
mengalami laju kenaikan harga rokok
terpenuhi saat sistemdp = — = — = dQ = 0. dt dt dt dt
Berdasarkan asumsi di atas, diperoleh satu titik
Q*
ini
keadaan
setimbang
kesetimbangan
E = (P *, L, S", Q *) dengan,
perokok,
yaitu
P*
φ(γ + d + μ + h)
(γ + d + μ + h)(d + μ + h) + β2
L* =___________________β'P___________________
(γ + d + μ + h )2 (d + μ + h) + β2 (γ + d + μ + h)
s * =_________________________γβ 2P_________________________
(δ + d + μ + h )(γ + d + μ + h )[(γ + d + μ + h)(d + μ + h )+ β 2 ]
(δ + h )γβ 2p + (δ + d + μ + h)hβ 2φ
(μ + d )(δ + d + μ + h )(γ + d + μ + h )[(γ + d + μ + h)(d + μ + h) + β ]
Setelah mendapatkan titik kesetimbangan, selanjutnya akan dilakukan analisis kestabilan
-
— β2 — 2( d + μ + h )(γ + d + μ + h) 2(γ + d + μ + h)
dari titik kesetimbangan perokok. Analisis kestabilan titik kesetimbangan perokok sebagai berikut:
—
(γ + d + μ + h)
2
0
0
—
(γ + d + μ + h)
2(γ + d + μ + h)
0
0
2
0
0
γ
—
(δ + d + μ + h)
0
h
(δ + h)
—
(μ + d)
Untuk mencari nilai eigen J (E), maka matriks tersebut ditulis sebagai berikut:
I λI — J (E )| = 0
(Z + (δ + d + μ + h )∖λ + (μ + d))
, 2 J (Z + d + μ + h )2 + β2 + 2( d + μ + h )(γ + d + μ + h) Z + Zl-----------------------------------------------
l 2(γ + d + μ + h)
+ ( β 2 + (d + μ + h )(γ + d + μ + h) ^
Ll 2 j
[(λ + (δ + d + μ + h )Xλ + (μ + d ))]r (Z) = 0 dengan, r (Z) = a, Z2 + α1 Z + a0 dengan, a 2 =1
=0 (1)
α1 =
(γ + d + μ + h )2 + β2 + 2( d + μ + h )(γ + d + μ + h)
a 0 =
2(γ + d + μ + h) β2 + (d + μ + h )(γ + d + μ + h)
Berdasarkan Persamaan (1) diperoleh nilai ⅛ dan ⅛, yaitu λ = -(δ + d + μ + h)<0 dan ⅛ = -(μ + d) < 0. Nilai-nilai eigen yang lainnya terdapat pada polinomial r (Z). Berdasarkan kriteria Routh-Hurwitz, diperoleh bahwa polinomial r(Z) memiliki nilai eigen dengan bagian real negatif karena a0 > 0 dan α1 > 0 sehingga titik kesetimbangan E dikatakan stabil asimtotik.
-
3.4 Solusi Numerik
Simulasi dinamika pada populasi perokok menggunakan matlab dilakukan dengan memvariasikan parameter-parameter yang mempengaruhi model tersebut. Pada simulasi ini, nilai awal yang digunakan adalah P = 50,dan L = 10, S = 25 dan Q = 15. Nilai awal di ambil sesuai dengan nilai parameter pada Soleh & Sazmita (2017) dan nilai h diambil sesuai proporsi acak.
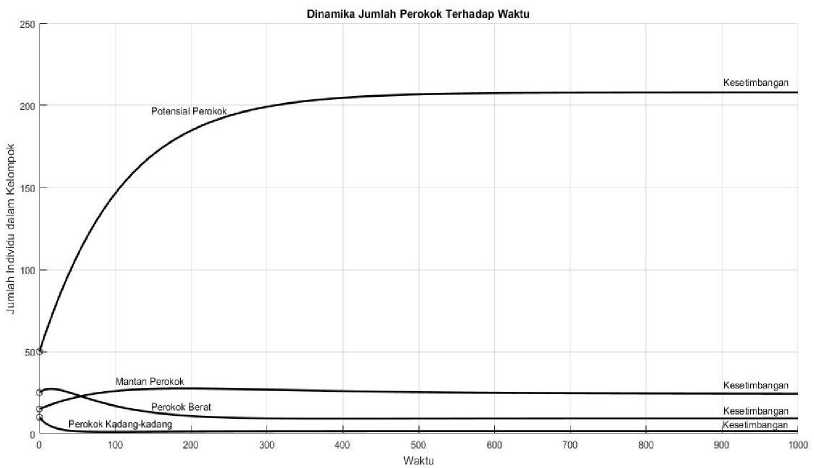
Gambar 1. Perilaku solusi terhadap garis kesetimbangannya dengan h = 0.006, φ = 2, β = 0.006, μ = 0.0021, d = 0.001, γ = 0.06, δ = 0.001
Berdasarkan Gambar 1, populasi potensial perokok mengalami peningkatan secara terus menerus karena adanya penambahan individu pada populasi (φ). Populasi perokok kadang-kadang mengalami penurunan, dikarenakan individu mengalami kematian secara alami ataupun kematian yang disebabkan oleh rokok dan kenaikan harga rokok, selain itu penurunan pada populasi perokok kadang-kadang juga dikarenakan oleh laju perubahan individu perokok kadang-kadang menjadi perokok berat. Populasi perokok berat akan mengalami penurunan karena adanya laju kematian alami, laju kematian karena rokok dan laju perpindahan perokok berat menjadi mantan perokok secara alami maupun karena kenaikan harga rokok. Sedangkan, untuk populasi mantan perokok atau individu yang telah berhenti merokok mengalami peningkatan. Peningkatan jumlah mantan perokok terjadi karena kenaikan harga rokok dan laju berhenti merokok sehingga individu perokok akan berhenti merokok.
Berdasarkan pembahasan tersebut, dapat disimpulkan bahwa model matematika jumlah perokok pengaruh kenaikan harga rokok dengan dinamika akar kuadrat memiliki satu titik kesetimbangan yaitu e = (p’,L,s’,Q’).
Titik kesetimbangan tersebut bersifat stabil asimtotik. Pada simulasi dapat disimpulkan bahwa populasi potensial perokok mengalami peningkatan secara terus menerus karena adanya penambahan individu pada populasi (φ). Populasi perokok kadang-kadang mengalami penurunan, dikarenakan individu mengalami kematian secara alami, kematian yang disebabkan oleh rokok dan kenaikan harga rokok, selain itu penurunan pada populasi perokok kadang-kadang juga dikarenakan oleh laju perubahan individu perokok kadang-kadang menjadi perokok berat. Populasi perokok berat akan mengalami penurunan karena adanya laju kematian alami, laju kematian karena rokok dan laju perpindahan perokok berat menjadi mantan perokok secara alami maupun karena kenaikan harga rokok. Sedangkan, untuk populasi mantan perokok mengalami peningkatan. Peningkatan jumlah mantan perokok terjadi karena kenaikan harga rokok dan laju berhenti merokok sehingga individu perokok akan behenti merokok.
Penelitian ini mengkaji model matematika jumlah peokok yang dipengaruhi oleh kenaikan harga rokok menggunakan dinamika akar kuadrat. Perlu dikembangkan dengan menambahkan beberapa asumsi, seperti individu yang telah berhenti merokok dapat kembali menjadi individu perokok. Asumsi
lainnya juga dapat ditambahkan dengan menjadikan individu perokok berat akan menjadi perokok kadang-kadang akibat kenaikan harga rokok, serta bisa menggunakan metode lain dalam proses penyebarannya.
DAFTAR PUSTAKA
Alkhudhari, Z., dkk. 2014. Global Dynamics of a Mathematical Model on Smoking. ISRN Applied Mathematics. 1-7.
Anggraini, M.V.Miswanto, dan Fatmawati. 2013. Analisis Model Matematika Jumlah Perokok dengan Dinamika Akar Kuadrat. Universitas Airlangga. 2(2), 10-20.
Castillo-Garsow, C., dkk. 1997. Mathematical Model for the Dyamics of Tobacco Use, Recovery and Relapse. MTBI.1-16.
Haris, A. dan Ikhsan, M. & Rogayah, R. 2012. Asap Rokok sebagai Bahan Pencemar dalam Ruangan. Universitas Indonesia-Rumah Sakit Persahabatan, :Jakarta.
Jami, Fitri Yessi. 2013. Model Matematika Pencegahan Pertambahan Jumlah Perokok dengan Penerapan Denda. UNP. Padang.
Mohamad, K. 2014. Fakta Tembakau dan Permasalahannya di Indonesia. Tobacco Control and Support Center: Jakarta.
Sharomi, O. & Gumel, A.B. 2008. Curtailing Smoking Dynamics: A Mathematical Modeling Approach. Applied Mathematics and Computation. Hal 475-499.
Soleh, Mohammad & Sazmita, Delli. 2017. Model Matematika Jumlah Perokok dengan Dinamika Akar Kuadrat dan Faktor Migrasi. Seminar Nasional Teknologi Informasi, Komunikasi dan Industri (SNTIKI).9,628-634.
Tirtosastro, S. & Murdiyati, A.S. 2010. Kandungan Kimia Tembakau dan Rokok. Buletin Tanaman Tembakau, Serat dan Minyak Industri. 2(1), 33-43.
Zeb, A., Bibi F., Zaman, G. 2015. Optimal Control Strategies In Square-Root Dynamics Of Smoking Model. International Journal of Scientific World. 3(1), 91-97.
287
Discussion and feedback