PEMODELAN KASUS PNEUMONIA PADA BALITA DI PROVINSI BALI MENGGUNAKAN METODE REGRESI NONPARAMETRIK B-SPLINE

E-Jurnal Matematika Vol. 9(3), Agustus 2020, pp. 197-204

DOI: https://doi.org/10.24843/MTK.2020.v09.i03.p299

ISSN: 2303-1751

PEMODELAN KASUS PNEUMONIA PADA BALITA DI PROVINSI BALI MENGGUNAKAN METODE REGRESI NONPARAMETRIK B-SPLINE

I Gusti Ayu Made Valentina Dewi^§, I Gusti Ayu Made Srinadi², Made Susilawati³

¹Prodi Matematika, Fakultas MIPA – Universitas Udayana [Email: igamvd@gmail.com] ²Prodi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi @unud.ac.id] ³Prodi Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@gmail.com] ^§Corresponding Author

ABSTRACT

Pneumonia is an inflammatory lung disease caused by bacterium Streptococcus pneumonia, Chlamydophila pneumonia bacteria, influenza virus, and fungi. Bali Provincial Health Service data in 2018 shows that one of the diseases that causes many deaths in children under five is pneumonia. This study aims to model the number of pneumonia cases in children under five in Bali Province in 2018 with six research variables, namely percentage of low birth weight, percentage of coverage of infants who receive vitamin A, percentage of infants who receive exclusive breastfeeding, percentage of under-five health services, percentage of villages that implement community-based total sanitation, and percentage of neonatal complications management. In the B-Spline function there are connecting points called knots. The best estimation of the B-Spline regression model is obtained from selecting the optimum knot point with the criteria for the value of generalized cross validation (GCV) and the selected mean square error (MSE) having the minimum value. The B-Spline regression model that is formed is the quadratic B-Spline model (order 3) with five knots resulting in an R² value of 87.79%.

Keywords: Bali, Generalized Cross Validation (GCV), Knots, B-Spline, Pneumonia.

• 1.    PENDAHULUAN

Regresi nonparametrik merupakan metode statistika yang dapat digunakan untuk mengetahui hubungan antara variabel terikat dengan variabel bebas yang dilandasi pada bentuk kurva regresi yang tidak diketahui serta tidak mengasumsikan pola data tertentu. Oleh karena itu, pendekatan regresi nonparametrik memiliki fleksibilitas yang tinggi karena data diharapkan menentukan sendiri bentuk estimasi kurva regresinya tanpa dipengaruhi oleh faktor subyektivitas dari peneliti. Salah satu pendekatan regresi nonparametrik yaitu regresi spline.

Regresi spline merupakan fungsi polinomial tersegmen atau terpotong, dalam fungsi tersebut terdapat titik-titik penghubung yang disebut titik knot. Titik knot atau titik penghubung merupakan titik fokus dalam fungsi spline sehingga kurva yang dibentuk akan tersegmen atau terpotong. Langkah-langkah yang dilakukan pada regresi spline yaitu menentukan titik knot dengan nilai generalized cross validation (GCV) yang

paling minimum. Adapun basis yang biasa digunakan pada pendekatan spline yakni basis spline truncated dan basis B-Spline (Lyche & Mørken, 2008). Fungsi basis truncated memiliki kelemahan, yaitu pada saat orde spline makin tinggi, titik knot yang banyak dan jarak knot yang terlalu dekat, maka akan membentuk matriks yang mendekati singular. Basis yang dapat menutupi kelemahan dari basis truncated yaitu basis B-Spline dikarenakan basis B-Spline memiliki keunggulan yakni dapat digunakan apabila orde pada Spline tinggi serta jarak knot yang berdekatan (Eubank, 1999).

Beberapa penelitian yang menggunakan metode regresi nonparametrik B-Spline yaitu penelitian oleh Budiantara dkk. (2006) yang menghasilkan nilai koefisien determinasi yaitu sebesar 99,7% dengan variabel terikat yaitu indeks prestasi kumulatif (IPK) dan variabel bebasnya yaitu nilai ujian masuk tulis. Pada penelitian ini penulis menggunakan metode B-Spline pada permasalahan penyakit pneumonia.

Pneumonia merupakan penyakit radang paru-paru yang diakibatkan oleh bakteri Streptococcus pneumonia, dan bakteri Chlamydophila pneumonia, virus influenza, dan jamur. Di Indonesia kasus pneumonia ditemukan sebanyak 478.078 kasus, di antaranya kasus pneumonia pada balita sebanyak 311.227, balita yang mengidap pneumonia berat sebanyak 7.882 dan 142 balita di antaranya meninggal dunia akibat penyakit pneumonia. Permasalahan ini juga merupakan permasalahan yang terjadi di Provinsi Bali itu dapat dilihat pada kasus penemuan pneumonia paling tinggi di Provinsi Bali terjadi pada tahun 2016 dengan jumlah 6.955 balita dan kasus terendah pada tahun 2015 dengan jumlah sebesar 2.350 balita. Penyebab kematian balita di Provinsi Bali tahun 2018 masih didominasi oleh pneumonia dengan persentase sebesar 8,5%; diare sebesar 2,1% dan selebihnya dari penyebab lain (Dinas Kesehatan Provinsi Bali, 2018).

Berdasarkan uraian dalam pendahuluan, penelitian ini bertujuan untuk mengetahui bagaimana model regresi nonparametrik B-Spline pada jumlah kasus pneumonia pada balita di Provinsi Bali pada tahun 2018.

Regresi nonparametrik merupakan metode statistika yang tidak mengacu pada parameter tertentu dan dilakukan untuk mengetahui hubungan antara variabel terikat dengan variabel bebas dengan dilandasi pada asumsi data yang diambil bersifat acak, dan bentuk kurva regresi diasumsikan mulus (smooth). Oleh karena itu, pendekatan dengan menggunakan regresi nonparametrik memiliki fleksibilitas yang tinggi karena data diharapkan mencari sendiri bentuk estimasi kurva regresinya tanpa dipengaruhi oleh faktor subyektifitas dari peneliti. Adapun bentuk umum dari model regresi nonparametrik sebagai berikut:

Vi = f(^χi) + ^εi dengan i = 1,2,..., n       (1)

dengan yi merupakan variabel terikat pada amatan ke-i, ×ι merupakan variabel bebas pada amatan ke-i, f(x_l) merupakan fungsi data yang tidak diketahui bentuk maupun pola datanya εt merupakan galat atau eror yang diasumsikan bersifat acak, bebas dan memiliki nilai harapan nol E(_iε) = 0.  Pada saat

persamaan model regresi (1) didekati fungsi B-Spline dengan orde m dan k titik knot, maka persamaannya dapat ditulis seperti berikut:

y = ∑K ^k βιB_l,_m(x_l++ ε_l ,i = 1,2.....n (2) dengan Bι_mι(x) merupakan basis B-Spline dan merupakan parameter regresi untuk B-

Spline. Untuk membangun fungsi B-Spline yang berorde m dengan k titik knot ki,k2 ,k₃ , -,kk dengan a<ξ₁<∙∙∙<ξ_k< b, terlebih dahulu didefinisikan knot tambahan sebanyak                                 2  ,

^yai^tu ζ(Q_rrlιi), ..., -ii, ^ξθ , kk+i, . , kkmm' dengan ξ₄m- i ) = • = k₀ = a dan k++i = ••• = k _++m = b. Nilai a biasanya diambil dari nilai minimum pada variabel X, sedangkan nilai dari diambil dari nilai maksimum pada variabel X. Menurut Eubank (1999) basis dari fungsi B-Spline pada orde m dengan titik-titik knot pada k_i,..., k_k didefinisikan secara rekursif sebagai berikut ini:

‰ (x) =

m-^T^ - i (x) + 7⅛^lSi+i ,m-i(x) Sl+m-l~Sl              Sl+m~Sl+ι

(3)

dengan l = —(m — 1),..., k, dan

B i, 100 = {

1,x c [ ki, ki+i] 0,

dengan m adalah derajat B-Spline, m = 2 memberikan fungsi B-Spline

(4)

untuk linear,

m = 3 memberikan fungsi B-Spline kuadratik,

dan m = 4 memberikan fungsi B-Spline kubik. Untuk menaksir koefisien pada persamaan (2), didefinisikan matriks:

B (Z)

B-(m-i), m(^xi),  B-Cm_2 ), m⅛),   ..... B-_κ, m(^χl)∙

[B-_(m_i), m(χJ, B--_m_i), _m⅛_ny ..... B-_Kim(x_ny

Jadi B(A) menurut Budiantara et al. (2006) adalah matriks berukuran n × (m + K)

Estimasi parameter β_λ diperoleh dengan menggunakan metode least squares spline. Estimator didapat dengan meminimumkan jumlahan kuadrat error atau residual sum of squares (RSS), sehingga didapat:

β = (B^τ_λB_λy ⁱ By_y                 (5)

^dengaⁿ β_λ =(^β_λi β22-βλ(m+k^βT

Estimasi model B-Spline pada regresi nonparametrik adalah:

y = B_λβ_λ

= B_λ((B_λ^τB_λ)- BBly)

= BB^τ_λB_λy 'By_y

= S_λy              (6)

dengan matriks =   (     )      simetris

dengan definit positif. Pemilihan model B-

Spline terbaik diperlukan titik-titik knot yang optimal. Salah satu metode yang dapat

digunakan dalam pemilihan titik knot yang

optimal adalah generalized cross validation

(GCV). Menurut Eubank (1999) metode GCV

dapat ditulis sebagai berikut:

GCV (A') =

M S E ( λ) (n~ ¹trace[l - S]))²

(7)

dengan MSE (λ) = n~ ¹ ∑^ ₁(Y_i-Y)²,     Y

merupakan estimasi dari λ yang terpilih, l merupakan matriks identitas, merupakan banyaknya data, λ merupakan banyaknya titik knot            (k _i, k ₂ ,k ₃,...,k_p)            dan

Sλ = B((BλBλ)^{1 1} B.p Pemilihan model terbaik B-Spline dilakukan dengan memilih nilai GCV dan nilai MSE yang paling minimum.

• 2.    METODE PENELITIAN

  • 2.1    Jenis dan Sumber Data

Data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari Dinas Kesehatan Provinsi Bali tahun 2018. Data sekunder yang digunakan berupa jumlah kasus pneumonia pada balita pada 57 kecamatan di Provinsi Bali tahun 2018.

• 2.2    Variabel Penelitian

Variabel terikat yang digunakan pada penelitian ini adalah jumlah kasus pneumonia pada balita pada 57 kecamatan di Provinsi Bali tahun 2018 (Y) dan persentase berat bayi lahir rendah (  ), persentase cakupan pemberian

vitamin A pada balita (  ), persentase bayi

yang mendapat ASI eksklusif (  ), persentase

pelayanan kesehatan balita (  ), persentase

desa yang melaksanakan sanitasi total berbasis masyarakat (  ) dan persentase penanganan

komplikasi neonatal (  ) merupakan variabel

bebas.

• 2.3    Metode Analisis Data

Teknik analisis data dilakukan dengan regresi nonparametrik B-Spline dan bantuan Program R-3.6.1. Adapun langkah-langkah analisis data yang dilakukan sebagai berikut:

• 1.    Menyajikan statistika deskriptif variabel terikat dan variabel bebas sebagai gambaran umum untuk mengetahui data tentang pneumonia pada balita di Provinsi Bali.

• 2.    Membuat basis fungsi B-Spline pada m orde dan k titik knot sesuai dengan persamaan (3).

• 3.    Mencari  matriks S^  yang memenuhi

persamaan (6).

• 4.    Mencari  titik knot  optimal dengan

menggunakan nilai GCV yang paling minimum sesuai dengan persamaan (7).

• 5.    Mencari nilai mean square error (MSE) yang paling minimum.

• 6.    Menghitung nilai koefisien determinan (R²).

• 7.    Memodelkan variabel terikat dan variabel bebas dengan regresi nonparametrik B-Spline dengan titik knot optimal.

• 8.    Menginterpretasikan model yang didapatkan dari regresi nonparametrik B-Spline dan menarik kesimpulan.

• 3.    HASIL DAN PEMBAHASAN

  • 3.1    Deskripsi Data

Variabel-variabel pada penelitian ini diringkas dalam statistika deskripsi pada Tabel 1. Statistika deskripsi dari variabel-variabel penelitian ini diproses dengan bantuan Program IBM SPSS Statistics 22.

Tabel 1. Statistika Deskripsi Jumlah Kasus Pneumonia pada Balita dengan Faktor-Faktor yang Diduga Berpengaruh.

Variabel	Statistika Deskriptif
	Min	Max	Mean	Simpangan Baku
Y	0	515	77,29	83,70
X1	0,11	6,28	3,25	1,55
X2	94,46	100	99,39	1,35
X3	45,36	92,56	69,61	11,80
X4	3,96	46,99	15,79	8,46
X5	0	100	89,35	20,30
X6	7,85	100	63,26	25,67

Kasus pneumonia pada balita tertinggi berdasarkan Tabel 1 ditemukan sebanyak 515 kasus dan kasus terendah yaitu 0 kasus. Data dari Dinas Kesehatan Provinsi Bali tahun 2018 menampilkan bahwa Kota Denpasar merupakan kota tertinggi kasus pneumonia pada balita karena ditemukan terdapat 1.908 penderita pneumonia balita dari 93.060 jumlah balita. Dari 1.908 balita penderita pneumonia di Denpasar terdapat 515 kasus pneumonia balita di Kecamatan Denpasar Selatan. Sedangkan di lain hal, Kabupaten Badung merupakan Kabupaten dengan kasus terendah pneumonia

pada balita yang ditemukan terdapat 0 kasus di dua kecamatan di Kabupaten Badung yaitu Kecamatan Kuta dan Kecamatan Kuta Utara.

Dinas Kesehatan Provinsi Bali tahun 2018 mengemukakan bahwa persentase bayi yang memiliki berat badan lahir rendah yaitu terendah 0,11% dan tertinggi sebesar 6,28%. Bayi dengan berat badan lahir rendah ditimbang dalam waktu satu jam pertama setelah bayi lahir dengan berat kurang dari 2.500 gram. Bayi dengan berat badan lahir rendah (BBLR) biasanya dapat terjadi pada bayi prematur, serta pada bayi yang mengalami hambatan pertumbuhan selama kehamilan. Bayi dengan BBLR memiliki kecenderungan menuju peningkatan terjadinya infeksi dan mudah terserang komplikasi, selain itu bayi juga dapat memiliki masalah gangguan pada sistem pernapasan, susunan saraf pusat, ginjal, dan lainnya. Di Provinsi Bali menurut Dinas Kesehatan Provinsi Bali tahun 2018 bayi dengan BBLR tertinggi terjadi di Kabupaten Buleleng yaitu pada Kecamatan Tejakula sedangkan bayi dengan BBLR terendah ditemukan di Kabupaten Badung tepatnya di Kecamatan Kuta Utara.

Kecamatan Kuta Utara merupakan kecamatan dengan persentase tertinggi pemberian cakupan vitamin A pada balita (6-59 bulan) dengan 35 kecamatan lainnya. Sedangkan terdapat persentase terendah pemberian cakupan vitamin A pada balita yaitu sebesar 94,48% dari 100% terjadi pada Kabupaten Buleleng yaitu di Kecamatan Sukasada. Pemberian vitamin A pada balita selain bermanfaat pada kesehatan mata juga dapat meningkatkan daya tahan tubuh balita dari penyakit. Pemberian vitamin A dilaksanakan di posyandu setiap enam bulan sekali yaitu pada bulan Februari dan bulan Agustus. Terdapat dua jenis vitamin A yang diberikan, yaitu yang berwarna biru untuk balita usia 6-11 bulan dan yang berwarna merah untuk balita usia 12-59 bulan. Selain pemberian vitamin A pada balita pemberian ASI eksklusif juga sangatlah penting untuk tumbuh kembang anak. Ditemukan persentase bayi yang mendapat ASI eksklusif tertinggi sebesar 92,56% terjadi di Kabupaten Jembrana yaitu pada Kecamatan Negara dan terendah sebesar 45,36% terjadi di Kota Denpasar yaitu pada Kecamatan Denpasar Timur. Pemberian ASI eksklusif pada bayi dari baru lahir sampai umur 6 bulan bertujuan untuk menjamin pemenuhan pertumbuhan dan perkembangan

bayi dikarenakan ASI mengandung kolostrum yang kaya akan antibodi karena mengandung protein untukdaya tahan tubuh dan pembunuh kuman dalam jumlah tinggi sehingga pemberian ASI eksklusif dapat mengurangi risiko kematian pada bayi (Dinas Kesehatan Provinsi Bali, 2018).

Pelayanan kesehatan balita adalah pelayanan kesehatan pada anak umur 12-59 bulan meliputi pemantauan pertumbuhan dan perkembangan anak. Pemantauan pertumbuhan minimal delapan kali setahun dilakukan dengan pengukuran berat badan pertinggi badan/panjang badan dan pelayanan kesehatan seperti pemberian vitamin A dua kali setahun pada setiap bulan Februari dan Agustus. Pemantauan perkembangan minimal dua kali setahun meliputi perkembangan gerak kasar, gerak halus, bicara dan bahasa, daya dengar dan daya lihat serta sosialisasi dan kemandirian dimana pemantauan perkembangan anak ini dilaksanakan melalui pelayanan Stimulasi, Deteksi dan Intervensi Dini Tumbuh Kembang (SDIDTK) minimal dua kali pertahun (setiap 6 bulan). Pelayanan SDIDTK dilaksanakan oleh tenaga kesehatan, ahli gizi, penyuluh kesehatan masyarakat dan petugas sektor lain yang dalam menjalankan tugasnya melakukan stimulasi dan deteksi dini penyimpangan tumbuh kembang anak. Oleh karena itu pelayanan kesehatan balita disetiap Kabupaten/Kota di Provinsi Bali harus terlaksana dengan baik dan merata, seperti pada Kabupaten Bangli yaitu pada Kecamatan Kintamani dengan persentase pelayanan kesehatan balita tertinggi sebesar 46,99% sedangkan persentase terendah sebesar 3,96% terjadi di Kabupaten Tabanan yaitu pada Kecamatan Selemadeg. Selain itu, program Sanitasi Total Berbasis Masyarakat (STBM) juga merupakan pendekatan untuk mengubah perilaku higienis dan saniter dengan tujuan untuk meningkatkan derajat kesehatan masyarakat. Menurut Peraturan Menteri Kesehatan Nomor 3 Tahun 2014 tentang Sanitasi Total Berbasis Masyarakat dalam pelaksanaannya berpedoman pada lima pilar yakni: stop buang air besar sembarangan, cuci tangan pakai sabun, pengelolaan air minum dan makanan rumah tangga, pengamanan sampah rumah tangga, dan pengamanan limbah cair rumah tangga. Menurut data Dinas Kesehatan Provinsi Bali tahun 2018 persentase desa yang melaksanakan sanitasi total berbasis masyarakat terendah dengan persentase sebesar 0% terjadi di Kota Denpasar pada Kecamatan

Denpasar Barat selain itu di Kota Denpasar juga terjadi persentase tertinggi desa yang melaksanakan sanitasi total berbasis masyarakat sebesar 100% yaitu di Kecamatan Denpasar Utara, Denpasar Timur dan 39 kecamatan lainnya di Provinsi Bali.

Persentase penanganan komplikasi neonatal tertinggi berdasarkan Tabel 1 sebesar 100% terjadi di Kabupaten Gianyar pada Kecamatan Payangan sedangkan persentase penanganan komplikasi neonatal terendah sebesar 7,85% terjadi di Kabupaten Buleleng pada Kecamatan Kubutambahan. Berdasarkan deskripsi data yang telah diuraikan, terdapat 57 objek penelitian pada kasus pneumonia pada balita di Provinsi Bali sehingga regresi nonparametrik yang dapat digunakan yaitu regresi nonparametrik Spline, dengan pengaplikasian regresi nonparametrik Spline tepat menggunakan basis B-Spline untuk menghindari matriks singular.

• 3.2    Pemilihan Titik Knot Optimal Regresi
  
  Nonparametrik B-Spline

Pemilihan titik knot optimal pada regresi nonparametrik B-Spline pada penelitian ini dilakukan dengan bantuan Program R-3.6.1. Selanjutnya diuraikan pemilihan titik knot pada masing-masing orde hanya dengan 5 kombinasi yang menghasilkan GCV paling minimum seperti pada Tabel 2.

Berdasarkan Tabel 2, diperoleh titik knot optimal menggunakan regresi nonparametrik B-Spline berada pada orde 3 dengan 5 titik knot. Titik-titik knot optimal berturut-turut terletak pada titik X1=2.43, 2.64, 3.33, 3.4 dan 3.61,

X2=97.73,	97.94,	99.03,	99.22	dan	99.39,
X3=64.71,	66.91,	69.43,	70.87	dan	72.26,
X4=9.65,	9.86,	12.59,	15.90	dan	16.72,
X5=59.01,	66.65,	70,	72.73	dan	80.50,
X6=42.70,	46.05,	61.65,	66.73	dan	67.40

menghasilkan GCV yang paling minimum sebesar 6614,65 serta nilai MSE paling minimum sebesar 841. Adapun model terbaik yang terbentuk dapat dinyatakan sebagai berikut:

^̂=441+5B-2,3( *1)+355B-ι,3( *1)-21B₀,3(*1)+

114B₁,3(*1)+191B₂,3(*1)-169B₂,3(*1)+

260B₄ ,3(Xl)+21B₅,3(Xl)+52B-2,3(X₂)-

589B-I,3(*2)+151B₀,3( X₂)-

93Bi,3(×2) - 63B₂,3(×2) - 474B₂,3(×2)+

96B₄,3(×2)-

111B₅,3(×2)-38B-₂,3(χ₂)-97B-ι,3(χ₂)-119B₀,3(χ₂ )

-241Bi,3⁽ X₂)-185B₂,3⁽X₂)82B₂,3⁽X₂)-65B₄ ,3⁽X₂ )

-165 ,( X₂)412   ,( X₄) - 316   ,( X₄)+154 ,( X₄ )

- 98 ,( X₄)-43 ,( X₄)+381 ,( X₄)-37B₄ ,3^(, )-56B₅,3^(, )-26B-₂,3^(, )-161B-I,3⁽X₅)-12B₀,3⁽ X₂)+30Bi,3⁽X₅)-264B₂,3⁽X₂)-167B₂,3⁽X₂)+156B₄ ,3⁽X₂)-146B₅,3(χ₂)-94B-₂,3(χ_b)-4B-I,3(χ_b)-220B₀,3( χ_b)-215Bi,3( χ_b)-145B₂,3(χ_b)-145B₂,3( χ_b)-165B₄ ,3(χ_b)-92B₅,3( χ_b )

Tabel 2. Nilai GCV Minimum, Titik Knot dan Orde Optimum pada Regresi Nonparametrik B-Spline.

Banyaknya Titik Knot	Orde	GCV
1	2	6775,07
2		6690,94
3		7182,97
4		7443,88
5		6636,04
1	3	6693,51
2		6625,73
3		7222.64
4		6667.67
5		6614,65
1	4	7005,58
2		6740,32
3		6903,79
4		7148,79
5		6967,52

• 3.3    Interpretasi Model Regresi Nonparametrik B-Spline Kuadratik dengan Lima Titik Knot

Interpretasi dari model terbaik regresi nonparametrik B-Spline diuraikan dengan mempertimbangkan nilai dari basis B-Spline yang diperoleh sehingga interpretasi model dapat diuraikan sebagai berikut:

• 1.    Apabila variabel     ^2 , ^3 ,    ,   , Xg

diasumsikan tetap, maka persentase berat bayi lahir rendah (BBLR) (Xj ) terhadap jumlah kasus pneumonia pada balita pada kecamatan ke- i di Provinsi Bali (Y_i ) adalah sebagai berikut:

^̂=441+5B-₂,3(*1 )             (8)

dengan

	⎧ (( 2 ,1,32 )) 2,0,11≤ Xi < 2,43
	0,	2,43 ≤ Xl < 2,64
	0,	2,64 ≤ X1 < 3,33
2,3(^l)=	0,	3,33 ≤ X1<3,4
	0,	3,4≤ X1 < 3,61
	0,	3,61 ≤ X1 < 6,28
	⎩0,	untuk X1 lainnya

^̂=441+21B_z ,3(*1)        (9)

dengan

B₅,₃⁽Xl ⁾

={ (⁽

0,

- 3,61)

2,67

3,61 ≤ Xl < 6,28

untuk X₁ lainnya

2.

Ketika persentase BBLR pada kecamatan ke-i di Provinsi Bali bernilai minimum yaitu 0,11%, maka nilai minimum tersebut disubstitusikan ke persamaan (8) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut meningkat sebanyak 5 kasus. Selain itu, ketika persentase BBLR pada kecamatan ke-i di Provinsi Bali bernilai maksimum yaitu 6,28%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (9) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut meningkat sebanyak 21 kasus. Dengan demikian, ketika persentase berat bayi lahir rendah (BBLR) meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

Apabila variabel Xj , ^3 , , , ¾ diasumsikan tetap, maka persentase cakupan balita yang mendapat vitamin A ( ^2) terhadap jumlah kasus pneumonia pada balita pada kecamatan ke- i di Provinsi Bali (Y_i) adalah sebagai berikut:

^̂=441+52B-2,3(¾) (10) dengan

B-2,3(X2 )
	(97,73 - (    3,27	h )) 2	, 94,46≤ X2 < 97,73
	0,		99,73 ≤ X2 < 97,94
=	0,		97,94 ≤ X2 < 99,03
	0,		99,03 ≤ X2 < 99,22
	0,		99,22 ≤ X2 < 99,39
	0,		99,39 ≤ X2 <100
	⎩0,		untuk X2 lainnya

̂=441-111B_s ,3(*2)      (11)

dengan

B_s ,3⁽¾⁾

={(⁽h

0,

- 99,39) 0,61

} ²

) ,99,39≤ X₂<100

untuk X₂ lainnya

Ketika persentase cakupan balita yang mendapat vitamin A pada kecamatan ke-i di Provinsi Bali bernilai minimum yaitu 94,46%, maka nilai minimum tersebut disubstitusikan ke persamaan (10) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut meningkat sebanyak 51 kasus. Selain itu, ketika persentase cakupan balita yang mendapat vitamin A pada kecamatan ke-i di Provinsi Bali bernilai maksimum yaitu 100%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (11) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 111. Dengan demikian, ketika persentase cakupan balita yang mendapat vitamin A meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

• 3.    Apabila variabel Xi , X₂ ,   _,   , Xe

diasumsikan tetap, maka persentase bayi yang mendapat ASI eksklusif ( ■^3 ) terhadap jumlah kasus pneumonia pada balita pada kecamatan ke- i di Provinsi Bali (Y_i ) adalah sebagai berikut:

̂=441-38B-2,3(X₃)(12)

dengan

B-2,3⁽X₃)=

⎧(⁽ 64 ^, 71~X₃)₎ ², 45,36≤ X₃ < 64,71 v 19,       ^,,,

^⎪  0,       64,71 ≤ X₃ <66,91

^⎪  0,       66,91 ≤ X₃ <69,43

0,       69,43 ≤ X₃ <70,87

⎪ 0,        70,87 ≤ X₃ <72,26

⎪  0,        72,26 ≤ X₃ <92,56

⎩ 0,       untuk X₃ lainnya

^̂=441-165B_s ,3(X₃)(13)

dengan

B_s ,3⁽X₃ ⁾

( X₃ - 72,26) ²

=(   ₂₀₃^{,  )}) , 72,26≤X₃ < 92,56

20,3

• 0,                 untuk X₃ lainnya

Ketika persentase bayi yang mendapat ASI eksklusif pada kecamatan ke- i di Provinsi Bali bernilai minimum yaitu 45,36%, maka nilai minimum tersebut

disubstitusikan ke persamaan (12) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 38 kasus. Selain itu, ketika persentase bayi yang mendapat ASI eksklusif pada kecamatan ke-i di Provinsi Bali bernilai maksimum yaitu 92,56%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (13) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 165 kasus. Dengan demikian, ketika persentase bayi yang mendapat ASI eksklusif meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

• 4.    Apabila variabel X₁ , X₂ ,   _,   , X₆

diasumsikan tetap, maka persentase pelayanan kesehatan balita (X4 ) terhadap jumlah kasus pneumonia pada balita pada kecamatan ke-i di Provinsi Bali (Yi ) adalah sebagai berikut:

̂ =441+412B-2,3( *4)      (14)

dengan

B-2,3( *4 )

⎧ (3,96 - *4 )2 ⎪⎧(   5,69   ) ,    3,96≤*4 < 9,65

⎪⎪  0,               9,65 ≤ *4 < 9,86

=   0,              9,86 ≤ *4 < 12,56

⎨  0,            12,56 ≤ *4 < 15,90

⎪  0,            15,90 ≤ *4 < 16,72

⎪  0,            16,72 ≤ *4 < 46,99

⎩0,               untuk X4 lainnya

̂ =441-56B_s ,3( *4)      (15)

dengan

B_s ,3⁽*4 ⁾

( *4 - 16,72) ²

=(   ₃₀₂₇^,  ) , 16,72≤X₄ < 46,99

30,27

• 0,                untuk X₄ lainnya

Ketika persentase pelayanan kesehatan balita pada kecamatan ke-i di Provinsi Bali bernilai minimum yaitu 3,96%, maka nilai minimum tersebut disubstitusikan ke persamaan (14) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut meningkat sebanyak 412 kasus. Selain itu, ketika persentase pelayanan kesehatan balita pada kecamatan ke- i di Provinsi Bali bernilai maksimum yaitu 46,99%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (15) sehingga ditemukan jumlah kasus pneumonia pada balita pada

kecamatan tersebut berkurang sebanyak 56 kasus. Dengan demikian, ketika pelayanan kesehatan balita meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

• 5.    Apabila variabel    ^l , %2 ,   ,   , ^6

diasumsikan tetap, maka persentase sanitasi total berbasis masyarakat (¾) terhadap jumlah kasus pneumonia pada balita pada kecamatan ke- i di Provinsi Bali (Yt) adalah sebagai berikut:

̂ =441-26B-2,3(X_z)       (16)

dengan

B-2,3(Xz )
	⎧ (0-k )) ⎪ ( 59,10 ) ,	0≤Xz < 59,10
	⎪ 0,	59,10 ≤ χz < 66,65
=	0,	66,65 ≤ χz <70
	0,	70≤Xz < 72,73
	0,	72,73 ≤ Xz < 80,50
	⎪ 0,	80,50 ≤ χz < 100
	⎩0,	untuk X5 lainnya

^̂ =441-146B_s ,3(X_z)         (17)

dengan

B_s ,3(X_z )

( X_z - 80,50) ²

₌{(   _19,5   ) ,  80,50≤X_z < 100

0,                untuk X₅ lainnya

Ketika persentase sanitasi total berbasis masyarakat pada kecamatan ke-i di Provinsi Bali bernilai minimum yaitu 0%, maka nilai minimum tersebut disubstitusikan ke persamaan (16) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 26 kasus. Selain itu, ketika persentase sanitasi total berbasis masyarakat pada kecamatan ke-i di Provinsi Bali bernilai maksimum yaitu 100%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (17) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut meningkat berkurang sebanyak 146 kasus. Dengan demikian, ketika persentase sanitasi total berbasis masyarakat meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

• 6.    Apabila variabel ^l , ^2 ,   ,   , ¾

diasumsikan tetap, maka persentase komplikasi neonatal balita (Xg ) terhadap jumlah kasus pneumonia pada balita pada

kecamatan ke-i di Provinsi Bali (Yi ) adalah sebagai berikut:

̂ =441-92B₄ ,3(*5)            (18)

dengan

B-2,3(^6 )

⎧ (7,85 - *6 )2 ⎪⎧(  34,85  ),  7,85≤*6 < 42,70

⎪⎪0,                42,70 ≤*6 < 46,05

=  0,               46,05 ≤ *6 < 61,65

⎨0,               61,65 ≤*6 < 66,73

⎪0,               66,73 ≤*6 < 67,40

⎪ 0,               67,40 ≤ *6 < 100

⎩0,              untuk X6 lainnya

^̂ =441-94B_s ,3(*6)           (19)

dengan

B_s ,3⁽^6 ⁾

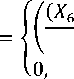
- 67,40) 32,6

67,40 ≤ *6 < 100

untuk X₆ lainnya

Ketika persentase komplikasi neonatal balita pada kecamatan ke-i di Provinsi Bali bernilai minimum yaitu 7,85%, maka nilai minimum tersebut disubstitusikan ke persamaan (18) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 92 kasus. Selain itu, ketika persentase komplikasi neonatal balita pada kecamatan ke-i di Provinsi Bali bernilai maksimum yaitu 100%, maka nilai maksimum tersebut juga disubstitusi ke persamaan (19) sehingga ditemukan jumlah kasus pneumonia pada balita pada kecamatan tersebut berkurang sebanyak 94 kasus. Dengan demikian, ketika persentase komplikasi neonatal balita meningkat, maka akan menurunkan jumlah kasus pneumonia pada balita di Provinsi Bali.

4. SIMPULAN DAN SARAN

Pada kasus pneumonia pada balita di Provinsi Bali menggunakan regresi nonparametrik B-Spline diperoleh model terbaik pada B-Spline kuadratik (orde 3) dengan 5 titik knot optimal, dengan nilai GCV sebesar 6614.65 serta nilai MSE sebesar 841 dan koefisien determinasi R² =0.8778634. Hal ini menunjukkan bahwa model kasus pneumonia pada balita di Provinsi Bali dengan menggunakan regresi nonparametrik B-Spline kuadratik (orde 3) mampu menerangkan 87,79% keragaman jumlah kasus pneumonia

balita pada 57 kecamatan di Provinsi Bali tahun 2018, sisanya 12,21% dipengaruhi oleh variabel lain di luar model.

Berdasarkan model yang didapat pada kasus pneumonia pada Balita di Provinsi Bali dapat disimpulkan bahwa penurunan persentase pelayanan kesehatan balita dapat meningkatkan kasus pneumonia pada balita sebesar 411 kasus di Provinsi Bali, sedangkan persentase balita yang mendapatkan ASI eksklusif dapat menurunkan kasus pneumonia sebanyak 165 kasus, sehingga dapat ditarik kesimpulan bahwa jika ingin menurunkan kasus pneumonia pada balita, haruslah para ibu memberikan ASI eksklusif pada balita serta tenaga kesehatan lebih meningkatkan pemantauan perkembangan dan pertumbuhan anak berusia 12-59 bulan setiap 6 bulan sekali agar kasus pneumonia pada balita di Provinsi Bali dapat menurun.

Pada penelitian selanjutnya diharapkan dapat mengaplikasikan analisis regresi nonparametrik spline dengan basis spline yang lain seperti basis I-Spline, M-Spline, P-Spline atau yang lain untuk meningkatkan signifikansi model pneumonia pada balita di Provinsi Bali.

DAFTAR PUSTAKA

Budiantara et al. (2006). Pemodelan B-Spline dan Mars Pada Nilai Ujian Masuk Terhadap IPK Mahasiswa Jurusan Disain Komunikasi Visual Uk. Petra Surabaya. Jurnal Teknik Industri VOL. 8, NO. 1, 113.

Dinas Kesehatan. (2018). Profil Kesehatan Provinsi Bali. Denpasar: Dinas Kesehatan Provinsi Bali.

Eubank, R. L. (1999). Nonparametric Regression and Spline Smoothing. New York: Marcel Dekker, Inc.

Kementerian Kesehatan RI. (2018). Data dan Informasi        Profil        Kesehatan

Indonesia.Jakarta: Kementrian Kesehatan RI.

Lyche, T., & Mørken, K. (2008). Spline

Methods Draft. Department of Informatics Centre of Mathematics for Applications University of Oslo

Misnadiarly. (2008). Penyakit Infeksi Saluran Napas Pneumonia pada Anak Balita, Orang Dewasa, Usia Lanjut : Pneumonia Atypik dan Pneumonia Atypik Mikobakterium. Jakarta: Pustaka Obor Populer.

204