SOLUSI DARI PERSAMAAN CAUCHY–EULER NONHOMOGEN KASUS LOGARITMIK

E-Jurnal Matematika Vol. 9(2), Mei 2020, pp. 125-133

DOI: https://doi.org/10.24843/MTK.2020.v09.i02.p289

ISSN: 2303-1751

SOLUSI DARI PERSAMAAN CAUCHY–EULER NONHOMOGEN KASUS LOGARITMIK

I Gede Putu Miki Sukadana^1§, I Nyoman Widana², Ketut Jayanegara³

¹Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: [email protected]]

²Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: [email protected]]

³Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: [email protected]]

^§Corresponding Author

ABSTRACT

Ordinary differential equation is one form of differential equations that are often found in everyday life. One form of ordinary differential equations which has non–constant coefficients is the Cauchy– Euler differential equation. In the nonhomogeneous Cauchy–Euler differential equations, the undetermined coefficient and the parameter variation were the most method that often used to find the particular solution. This paper aimed to show a new solution that was shorter than the previous methods for nonhomogeneous Cauchy–Euler differential equations with the right side was a logarithmic form. The new solution had been proven to produce the same solution as the ordinary solution sought using the undetermined coefficient method.

Keywords: Cauchy–Euler differential equation, nonhomogenous differential equations, logarithmic form, particular solution

• 1.    PENDAHULUAN

Persamaan diferensial merupakan salah satu konsep matematika yang banyak digunakan dalam ilmu pengetahuan seperti fisika, kimia, industri dan teknik. Persamaan diferensial adalah persamaan yang melibatkan variabel–variabel tidak bebas dan derivatif– derivatifnya terhadap variabel bebas. Persamaan diferensial dibagi menjadi dua jenis, yaitu biasa dan parsial (Edwards & Penney, 2008).

Persamaan diferensial biasa (PDB) adalah suatu persamaan diferensial yang melibatkan hanya satu variabel bebas (Chapra & Canale, 2015). Penerapan persamaan diferensial dapat ditemukan pada pemodelan perhitungan populasi maupun peluruhan. Salah satu bagian dari PDB adalah persamaan diferensial Cauchy– Euler.

Persamaan diferensial Cauchy–Euler adalah persamaan diferensial biasa (PDB) berorde– n yang menyerupai persamaan polinomial (Batiha & Batiha, 2011). Penelitian sebelumnya dilakukan oleh Dev dan Gleiser (2002) yang menggunakan persamaan diferensial Cauchy– Euler tentang efek dari tekanan pada sifat–sifat benda yang diasumsikan simetris berbentuk

bola dan terikat oleh gravitasi, seperti bintang. Penelitian tersebut menunjukkan bahwa persamaan diferensial Cauchy–Euler berguna untuk menjelaskan fenomena mengenai gravitasi pada bintang.

Penelitian lainnya yang dilakukan oleh Sabuwala dan Leon (2011) mengenai solusi khusus persamaan Cauchy–Euler polinomial nonhomogen. Penelitian tersebut menghasilkan suatu rumus solusi khusus yang baru untuk menyelesaikan persamaan diferensial Cauchy– Euler polinomial nonhomogen.

Berdasarkan uraian tersebut penulis melakukan modifikasi kasus pada persamaan diferensial Cauchy–Euler,yang ruas kanannya berbentuk logaritma natural terhadap suatu variabel pada persamaan tersebut. Persamaan yang berisi logaritma natural ini merupakan kasus khusus dari persamaan diferensial Cauchy–Euler.

• 2.    METODE PENELITIAN

• A.    Jenis dan Sumber Data

Penelitian ini dilakukan dengan mengkaji beberapa literatur berupa buku, jurnal maupun laporan penelitian yang relevan dengan topik

yang akan dibahas. Langkah awal dalam penelitian ini adalah mempelajari konsep dasar dari persamaan diferensial yang akan digunakan dalam penelitian, meliputi persamaan diferensial biasa dan persamaan diferensial Cauchy-Euler beserta beberapa teori terkait, yaitu fungsi logaritma, turunan fungsi logaritma beserta contohnya.

Setelah mempelajar konsep yang berkaitan, langkah selanjutnya adalah mencari solusi khusus persamaan diferensial Cauchy–Euler dengan ruas kanan persamaannya adalah bentuk logaritma.

• B.    Teknik Analisis

Langkah-langkah yang dilakukan adalah sebagai berikut:

• 1.    Menyajikan dua kasus persamaan diferensial Cauchy–Euler yang akan dibahas

• 2.    Mencari solusi untuk masalah dengan bentuk yang sederhana.

• 3.    Menjabarkan beberapa bentuk teorema pendukung sesuai dengan permasalahan.

• 4.    Membentuk solusi untuk kasus umum dari permasalahan.

• 5.    Membuktikan solusi yang diperoleh.

• 3.    HASIL DAN PEMBAHASAN

• a.    Bentuk Permasalahan

Masalah yang dibahas pada penelitian ini adalah persamaan diferensial Cauchy–Euler dengan bentuk sebagai berikut: n         m

∑ a_it^ly⁽ⁱ)=∑^bJ ln(Cjt)

I=O            j=0

Proses pencarian solusi dari persamaan tersebut dimulai dengan memberikan beberapa contoh kasus yang menggunakan persamaan tersebut.

• b.    Contoh Kasus yang Digunakan

Dalam membentuk solusi persamaan diferensial Cauchy–Euler, ditampilkan terlebih dahulu kasus–kasus yang menggunakan persamaan diferensial Cauchy–Euler sebagai berikut.

Contoh kasus:

• 1.    Tentukan solusi khusus dari 2t²y"+7ty' + 10y=3ln2t.

• 2.    Tentukan solusi khusus dari 3t³y"' + 6t²y"+5ty' +9y=2ln5t+ 7ln3t-11ln7t.

Penyelesaian dari kasus di atas dijabarkan sebagai berikut.

1. Tentukan solusi khusus dari 2t²y”+7ty' + 10y=3ln2t.

Penyelesaian:

Misalkan: X =ln2t diperoleh:

dx dt

1    d²x     1

= dan   =--7 ,

t      dt²      t²

Diperoleh pula

dy dy dx dy11dy

^,

d²y  d ⁽dt ⁾

dt² dt

1 f d²ydy∖ t^{2 (}dx² dx ),

Dengan mensubstitusikan x, y', y” ke dalam persamaan yang diberikan maka diperoleh:

2‘2 ( .	1(⅛ - ⅛))+7t (1 ⅛)+10y 2∖dx2 dxJl     \t dx)		=3X
	d2y	dy dy
⟺	2 dx2	-2  +7  +10y dx dx	=3X
⟺		d2y   dy 2 ∕√-v2 +5   +10y dx2    dx	=3X

Selanjutnya misalkan y=    + bx +C

diperoleh

dyd

rl 'v  =2ax +bdan=2

dxdx

dyd

Dengan mensubstitusikan bentuk y, danke

ClXClX

dalam persamaan sebelumnya diperoleh

⟺

⟺

⟺

d²y dyO

2    +5   +10y⁼3X

dx² dx

2(2a)+5(2ax +b)+10(ax² + bx +c) =3x 4a+10ax+5b+10ax² +10bx+10c=3x

10ax²+(10a+10b)x+(4a+5b+10c) =3x

dengan mencocokkan masing masing suku yang bersesuaian diperoleh:

I.

⟺ II.

⟺

⟺

10a=0

a=0

10a+10b =3

0+10b =3

b ³

=₁₀

III.

⟺

⟺

4a+5b+10c=0

0+5(₁³₀)+10^c=0

15

₁₀+10^c=0

⟺

10C=-

⟺

_-

15

10

15

100

=¹( ⅛ -3  +2 ⅛ )

t^{3 (    -      +    )}

dengan mensubstitusikan bentuk y, y', y”,dan y'” ke dalam ruas kiri persamaan (4.1), (4.2), dan (4.3) diperoleh

3t³y'"+6t²y"+5ty' +9y

Selanjutnya substitusikan nilai a,b,c ke dalam bentuk y yaitu:

y=    + bx +C

3        15

=0+₁₀^x+(-₁₀₀)

1 d³y =3t³ ∙ -(   -

t³ ∖dx³

3d²y dx²

+2T) dx /

+6t²1( ⅛ - ≤ )+5t∙¹( ^)+9y t²∖dx² dx) t\dx)

d³y

= 3——

⁼³

_-

d²y dy

3   +5  +9y

dx² dx

3 ⁼10

3

_-

15

100

=₁₀ln2^t

_-

15

100

(4.1)

Sehingga diperoleh

A. Misalkan X=ln5t maka persamaan (4.2) dapat ditulis sebagai

2. Tentukan solusi khusus dari 3t³y"' + 6t²y"+5ty'+9y=2ln5t+

7ln3t-11ln7t

d³y

3——

³

_-

d²y dy

3   +5   +39y=2X   (4.5)

dx² dx

Penyelesaian:

Persamaan diferensial Cauchy–Euler menjadi tiga bagian, yaitu

A.3t³y'"+6t²y"+5ty' +9 =

2ln5t

B. Misalkan X =ln3t maka persamaan (4.3) dapat ditulis sebagai

dipecah

d³y

3——

³

_-

d²y dy               „

3   +5   +9y=7x (4.6)

dx² dx

(4.2)

C. Misalkan x=ln7X maka persamaan (4.4) dapat ditulis sebagai

B. 3t³y^,"+6t² 7ln3t

C. 3t³y'"+6t² -11ln7t

y"+5ty'+9 =

y"+5ty'+9 =

Misalkan x =lnkt diperoleh

dx 1 d²x

^{= ,    =}

1     d³x2

- dan=

t²      dt³t

(4.3)

(4.4)

diperoleh pula

y'

dy dy dx dy 1

_∙

_∙

y”

dt dx dt dx t d²y d ⁽ dt ⁾ dt² dt

d (¹ r)

_ \tdxj

1 dy t dx

y”

d³y

3——

³

_-

d²y dy                „

3   +5   +9y=-11x   (4.7)

dx² dx

Selanjutnya misalkan y=    + bx² + CX +d

diperoleh

dy dx d²y dx² d³y dx³

=3ax² +2bx +c,

=6ax+2b,

=6a,

dy d^y d^y

Dengan mensubstitusikan bentuk ,   ,   ,

dx dx² dx'

ke dalam ruas kiri dari persamaan (4.5), (4.6),

(4.7) diperoleh

d³y

3——

³

_-

dt

=¹(   _-  )

t^{2 (    -   )}

d²y dy

3   +5  +9y

dx² dx

d³y

^{=   =}

^d(dt^{2 )}

dt

d(1 (⅛ - 3^z ))

V ∖dx² dx)J

=3∙6a-3(6ax+2b)

+5(3ax² +2bx +c)

=+9(ax³ + bx² + CX +d)

=9ax³+(15a+9b)X²

= +(-18a+10b+9c)x

= +(18a-6b+5c+9d)

dt

Berdasarkan penjabaran di atas, persamaan (4.5), (4.6), dan (4.7) dapat ditulis menjadi bentuk persamaan umum, yaitu:

9ax³ +(15a+9b)x²

+(-18a+10b+9c)x

+(18a-6b+5c+9d)=px

dengan mencocokkan masing–masing suku yang bersesuaian diperoleh

p a b

C

d

y_B

=7 =0 =0 =^p =₉

_-

7

9

5

81 ^p

35

_-

81

I.	⟺	9a =0 a =0
II.		15a+9b =0
	⟺	0+9b =0
	⟺	b =0
III.		-18a+10b +9c =
	⟺	0+0+9c =
		P
	⟺	C =9
IV.		18a-6+5c+9d =0
	⟺	0-0+5(9)+9d =0
		5
	⟺	-P+9d =0
		5
	⟺	9d =- P
		5
	⟺	d
		=  81

=    + bx² + CX +d

7       35

=0+0+₉¹+(-₈₁)

7

=₉ln3^t-

35

81

C. Untuk persamaan (4.7) dapat dicari solusi khusus sebagai berikut

d³y 3——

³

_-

d²y dy

3   +5  +9y=-11x

dx^z dx

P =-11

a =0

b =0

c

d

y_c

p 11

=₉=-₉

5     55

=-₈₁^{p =}81

=    + bx² + CX +d

11     55

=0+0+(-₉)¹⁺81

11

55

Ini berarti,

A. Untuk persamaan (4.5) dapat dicari solusi khusus sebagai berikut

-₉ln7^t+81

d³y

3——

³

_-

d²y dy

3   +5  +9y=2x

dx^z dx

p a b

c

=2 =0 =0 = v =₉

d

_-

2 ⁼9

5

81 ^p

_-

10

81

y_A

=    + bx² + CX +d

2       10

=0+0+₉¹+(-₈₁)

2

=₉ln5^t

_-

10

81

B.

Untuk persamaan (4.6) dapat dicari solusi khusus sebagai berikut

Diperoleh

yp =   + Vb + y_c

2

= ln5 t-1081+79ln3t - 3581

1155

=+(- ln7^t)+81

2       7       1110

= ln5t + ln3t-₉ln7t+₈₁

Dalam pembahasan akan memakai teorema– teorema berikut:

Teorema Turunan Logaritma Orde ke – i

Diberikan y =Aln(kt)+B

maka ⁽ _{i )}   (-1) ⁱIl ⁽i-1)!

maka ⁽⁾ =             A

Bukti:

Teorema ini akan dibuktikan menggunakan induksi matematika

d³y

3——

³

_-

d²y dy

3   +5  +9y=7x

dx^z dx

Untuk i=1 maka

1

y' =   =

t

A

t

Di lain pihak

y' (-1)   (1-1)!

t

(-1)⁰0!

=

t

1×1

=

t

_A ⁼

Terbukti benar untuk i=1

Selanjutkan diasumsikan benar untuk i= sehingga

d^{n 1}y

dtⁿ~¹

n-l

^{= 1}1 _∑

i=i

pi-i ( Il

_-

2, n-2)

( -1)!

(-1)

dx’

Akan dibuktikan untuk k= berlaku

dⁿy di”

n

=¹∑ tⁿZ-_l i=i

pi-ι ( Il-1,Il-1)(-1)ⁿ~’ d’y

( -1)!

dx’

(_k) ₌(-1)k-l ⁽k-1)! y ⁼

Akan dibuktikan untuk i=  +1.

dⁿy di”

d( y

(      )

dt

d( _i ¹ )∑Ij = I

P⁽i-i)₍Il-2,Il-2)

( -1)! dt

y(k+l)  ₌(

(-1)^k~¹ (k-1)! t^k

^A)

(-1)n-i-l d^y

(-1)

= ((-1)k-l (k-1)!At~^k)

= (-1) k-l (k-1)!A (-k)t~^k~¹

(-1)^k~¹(-1)(k-1)!kA ⁼

(-1)^kk!A

⁼

Di lain pihak

1

⁺ tⁿ~¹ d (∑ Pi

_∙

⅛) dx’)

P⁽i-i)₍Il-2,Il-2)

( -1)! dt

(-1) n-j-1

Teorema Turunan Orde ke–k

Jika x=lnbt,y=(t) dan k=1,2,⋯ maka k

d^ky 1   P^j-¹ (k-1,k^-1)(-1)k-i^Z

clt^ ^{=  ∑}     ( -1)!     ^(-1)

J=I

n-l

= ¹ ∑( ⁿ

i=i

-1)

P⁽i-i)₍n-2,n-2)

Bukti:

Akan dibuktikan menggunakan induksi matematika.

Untuk k=1

dy  1P(0,0)(-1)⁰ dy

Akan dibuktikan =

dt t 0! dx

11(-1)⁰ dy

=    0! dx

1 dy t dx

n-l

^{+ 1} . ∑

i=i

( -1)!

. d’y

(-1)

dx’

P⁽i-i)₍Il-2,Il-2)d’^y

1 = (-1) n-j-1 ∙

n-l

= ¹ ∑( ⁿ-1) i=l

. d’y

= (-1)ⁿ~^jT7 ClX ^]

1 ⁿ~ι

( -1)!

dx’⁺¹

P⁽i-i)₍ n-2,n-2)

P⁽i-i)₍ n

_-

( -1)!

2, n-2)

x dx dt dy dt

=lnbt

1

⁼

dy dx

dx dt

1 dy t dx

i=i

(-1) n-j-l

( -1)!

dx’⁺¹

dengan menguraikan diperoleh

(4.9)

Terbukti untuk k=1

Asumsikan benar untuk k=  -1 yaitu

n-l

∑(n-1) i=i

P⁽i-i)₍ n-2,n-2)

( -1)!

. d’y

(-1)

dx’

(n-1)P(n-2,n-2) _- n-l^dy 0!          ^(-1)

n-l

+∑(Tl-1)

P⁽J-ι)₍Il-2,Il-2)

( -1)!

=¹(∑

V=¹

Terbukti.

P⁽j-i)₍Tl-1,Tl-1) ( -1)!

(-1)ⁿ~ⁱ^)

dx^j I

■ (Vy

(-1)

dx^J

P(n-1,n-1)

Teorema Penjumlahan Turunan Orde ke–k

0! n-l

+∑(n-1)

1=2

. d^Jy (-1)

dx^J

(-1) ⁿ~¹7Γ dx

Jika x=lnbt maka

sehingga

P⁽J-I)₍ n-2,n-2)

( -1)!

ⁿ

∑ ÷k^d y

k=l n k

=∑∑a_k

P⁽J-T)₍ k-1,k-1)

( -1)!

(-1)

dx¹

yp⁽  )₍ 2-2,Tl^-2)(-1)_n-_j-₁d^y

( -1)!               dχj+ι

Bukti:

n

=∑

J=2 n

=∑

J=2 n

=∑

}=2 n-l

=∑

}=2

p⁽j 2)₍Tl-2,Tl-2) _- n-j-2^d y

( -2)!      ^(-1) dχi

( -1)P⁽ J-2)₍Tl-2,Tl-2)(-1)ⁿ~i Vy

( -1)( -2)!

( -1)P⁽ j~2)₍Tl-2,Tl-2)

( -1)!

( -1)P⁽ j~2)₍Tl-2,Tl-2)

(-1)² dχi . di y (-1)n-j? dx^J

+

( -1)!

. di y (-1)n-j? dx^J

( Tl-1)P⁽ n-2)₍Tl-2,Tl-2)

n-l

=∑

J=2

( Tl-1)!

diy

- n-n__i

^(-1)

( -1)P⁽ j-2)₍Tl-2,Tl-2)

( -1)!

. di y (-1)n-j? dx^J

+

P⁽ n-l)₍Tl-1,Tl-1)dⁿy

Kembali ke (4.9)

( Tl-1)!      dxⁿ

ⁿ             Is

∑ _tk^d y ^ak dv

n

k

=∑ <v* ¹ ∑ k=l       j=l

P⁽j-i)₍ k-1, ( -1)!

k-1)

(-1)^k-i — ^{( 1)}

^p⁽ J-i)₍ k-1,k-1)

= ∑  _∑     (_{( -1}1₎,_!   1)

= (-1)

∑∑   ⁽J-T)₍k-1,k-1)

(_{( -1}1₎,_!    1)

= (-1)

Terbukti benar.

n-l 1_∑ tⁿ La

( Tl-1)P⁽j-i)₍Tl-2,Tl-2)

1

( -1)!

P⁽j-i)₍Tl-2,Tl-2) ( -1)!

(-1)n-j_L

^{( 1)}

. ₁ d^j+1y

(-1)n-J-I---_L

^(-1)

(

^∑

( Tl-1)P⁽i~¹ )₍Tl-2,Tl-2) ( -1)!

(-1)n-j

+ ∑P⁽  )₍ 2-2,Tl ^-2)(-1)n-j-1

dx^]+∑     ( -1)!     ^(-1)

J=T

d>»y

)

Teorema Superposisi

Jika f= adalah solusi dari n

∑ 9if ⁽ ' )_=ℎ

I = O

dan f= adalah solusi dari n

∑ 9if ⁽ ‘ )_{=ℎ 2}

1 = 0

maka f=   +f2 adalah solusi dari

n

∑ 9if ⁽ ‘ ⁾=ℎ₁ +ℎ₂

1 = 0

Bukti:

f (i)₌ f ⁽i⁾+

J =+

nn

⟺∑9ifι^{( 1} )₊∑9i⅛^{( 1} )_=ℎ1 +ℎ₂

1 = 01 = 0

n

⟺∑9i (Λ^{( 1} )₊Λ^{( 1 )})=ℎ₁ +ℎ₂

i=o

n

⟺∑Pif⁽ ‘ )_=ℎ1+ℎ ₂

1 = 0

Terbukti.

Teorema 1

Diberikan persamaan diferensial Cauchy–Euler nonhomogen dengan ruas kanan adalah suatu logaritma, yaitu n

⟺ a₀rx+(∑a_i (i-1)!(-1)i I_r +S)=bx

Diperoleh:

a₀rx = b

⟺ =

^αo

Akibatnya

n

∑ a_i (i-1)!(-1)I I_r +S=0

1=1

∑ a_it^ly⁽ⁱ)₌b ln(ct)

(4.10)

Maka solusi khususnya adalah

n

y_P =  ln(Ct)-4∑ a_i(-1)i-i (i-1)!

a₀            Z-∣

i=i

Bukti:

Pertama persamaan 4.10 dipecah menjadi:

(∑ a_it^ly⁽ⁱ))₊a₀y = ln(ct)       I

(4.11)

Misalkan X =lnCt dan berdasarkan teorema penjumlahan turunan orde ke–k, persamaan (4.11) dapat ditransformasi menjadi

n i

∑∑a_i i=l7=1

p⁽J-ι)₍i

_-

1, i-1)

( -1)!

. . d’y

(-1)

dx¹

=

_-

_-

n

∑ a_i (i-1)!(-1)i ι_r

i=i n

r∑ a_i(-1)i-i (i-1)!

i=i n

_∑ a_i(-1) ■ -1 (i-1)!

Solusinya berupa

y

=  +S

b

= ln ct

^αo

Terbukti.

Teorema 2

Berikut

_-

n

1∑ a_i(-1) i-i (i-1)!

^a°⅛

akan diuraikan persamaan

+ ^ao y =

Bentuk di atas adalah diferensial nonhomogen

(4.12) bentuk persamaan dengan ruas kanan

diferensial Cauchy–Euler yang berisi logaritma natural dan merupakan masalah inti yang ingin dijawab. Diberikan persamaan diferensial Cauchy–Euler berbentuk

n

m

berbentuk polynomial sehingga solusinya dapat dibentuk menjadi bentuk polynomial, yaitu: y=  +s

dy

=

dx

d^Jy

=0,j=2,3,⋯,n

dx¹

Dengan mensubstitusikan solusi bentuk polinomial dan turunannya ke dalam persamaan (4.12) maka diperoleh:

∑ a_it^ly^{( 1} )=∑^bJ ln(Cjt)

i=0

J=O

Dengan solusi khusus

m

y_P =∑  lnCjt

J=O

■o

- ¹ (∑ ⁴' )(∑«_t(-1) “ ⁽ ' -1)!)

ⁿ / ∑(

I=I ^x

aiP (i-1,i-1)

0!

(-1)I I_r+0)

+ «0 (rx +s)=bx n

⟺∑at (i-1)!(-1)I I_r + a₀rx +s=

Akan dibuktian rumus di atas Bukti:

n

m

i=o

Dipecah menjadi

n

∑ a_it^ly^{( 1} )=∑^bJ ln(Cjt)

J=O

∑ a_it^ly⁽¹)  ₌ ^O ln( £"0 £ ) memiliki solusi

i=o

7o =   ln(^cot)- „2 ∑ a_i(-1) i-ι (i-1)!

^ao          ^ao γ~!

n

∑ a_it^ly^(l)  = bi ln(Cy t) memiliki solusi

i=o

b₁ \ b± V

yi =   ln(Cy t)-4∑ a_i(-1) i—i (i-1)!

^ao        ^aO ^¹

n

∑ a_it^ly⁽¹⁾ = b-rn ln(Cjyy ) memiliki solusi

n

y_m =   ln(c_mt)-   ∑ at(-1)t-i (i-1)!

^ao           ^αo

Menurut prinsip superposisi akan membentuk

Contoh kasus:

• 1.    Tentukan solusi khusus dari 2t²y"+7ty^r + 10y=3ln2t.

• 2.    Tentukan solusi khusus dari 3Cy^rrr + 6t²y^rr+5ty^,+9y=2ln5t+ 7ln3t-11ln7t.

Solusi dari kasus yang diberikan adalah sebagai berikut :

1. Diketahui 2t²y^rr+7ty'+10y=3ln2t

^aO =10 a₁=7  «2 =2 b=3 c=2

Sehingga solusi khususnya berupa

m

∑

r ln(Cjt ⁾

j=o ⁰

Vv =  + Vi +⋯Vm

( T ln(C₀1)-⅛ ∑ a_l (-1) :-l ( i - 1)!)

ξ⅝      ^o 4           /

(

- ln(Cy t)-⅞ ∑ a_i (-1) t-i (i-1)!

®o         ⅝ ^zt

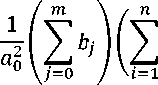
a_i(-1)   (i-1)!)

1

=   ln(ct)--(b)(a₁(-1) 1-1(1-1)!

«o         «0

+ «2 (-1) 2-1(2-1)!)

+⋯

=+(bm ln(Cτ∏t)-   ∑ a_i(-1)^¹ ( i

∖^0         ^o ~^

- 1)!)

=∑ ⅛ ln(Cjt ⁾

=- ¹ (∑⅛)(∑ (-1)  ^{( ;}

- 1)!)

Jadi solusi khusus yang diberikan terbukti benar.

Berikut ini teorema 1 dan teorema 2 digunakan untuk menyelesaikan persamaan

3

=₁₀ln(2 ')

1

=-   ∙3(7∙1∙1+2(-1)∙1)

10 ^z

31

=₁₀ln2 ' -₁₀₀∙3(7-2)

3

₁₀ln2 ' ^-

15

100

(4.14)

2. Diketahui 3t³y^rrr+6t²y^rr+5ty'+9 =

2ln5t+7ln3t-11ln7t

cLq =9 CCy =5 bo =2  bi=7

Cq =5    =3

¾ =6 b₂ =-11

C₂ =7

^a3 =3

Sehingga solusi khususnya berupa

y_P

diferensial Cauchy-Euler pada dua kasus yang sebelumnya telah diselesaikan dengan metode biasa.

Untuk pembuktian solusi khusus baru yang telah dibentuk maka solusi khusus tersebut diterapkan pada contoh kasus yang telah diberikan sebelumnya.

=(h ln(c₀t)+h. ln(Cy t)+— ln(c₂t)

∖CIq              CIqCLq

. b₂1

=+  ln(^c3^))-—(bo + bi + b₂ )

^aO/

=∙(a₁(-1) 1-1(1-1)!

=+α₂ (-1) 2-1(2-1)!

=+a₃ (-1) 3-1(3-1)!)

2        711

=( ln(5t)+ ln(3t)-₉ln(7t)

01

=+ ln(0t))-  (2+7-11)

981

=∙(5(1)1+6(-1)∙1+3∙1∙2) 27

=  ln5t+ ln3 t

11       10

=- ln7t +                   (4.15)

Diperoleh bahwa solusi khusus yaitu persamaan (4.1) sama dengan (4.14) dan persamaan (4.8) sama dengan (4.15). Jadi terbukti bahwa solusi khusus baru sama dengan solusi khusus yang diperoleh dengan cara biasa.

• 4.    KESIMPULAN DAN SARAN

Berdasarkan uraian pada hasil dan pembahasan, berikut diberikan kesimpulan dan saran sehubungan dengan penelitian.

Kesimpulan

Solusi khusus yang diperoleh pada penelitian ini mampu menyelesaikan persamaan diferensial Cauchy–Euler yang ruas kanannya berbentuk logaritma. Solusi tersebut sudah dibuktikan dan sama dengan solusi yang diperoleh dengan menggunakan langkah biasa. Keunggulan solusi baru ini adalah bentuknya yang lebih sederhana dan lebih cepat daripada solusi khusus dengan langkah biasa.

Saran

Berdasarkan hasil yang telah diperoleh, penulis sudah melakukan perhitungan abstrak untuk mencari dan membuktikan solusi yang diinginkan serta hasilnya sudah teruji. Disarankan untuk penelitian selanjutnya yaitu dengan mengambangkan bentuk logaritma natural agar lebih kompleks seperti perpangkatan pada logaritma natural.

DAFTAR PUSTAKA

Batiha, K. & Batiha, B., 2011. A Reliable Algorithm For Solving Cauchy-Euler Differential Equation. Australian Journal of Basic and Applied Sciences, 5(11), pp. 2161-2169.

Chapra, S. C. & Canale, R. P., 2015. Numerical Methods for Engineers. 7 ed. New York: McGraw-Hill Education.

Dev, K. & Gleiser, M., 2002. Anisotropic Stars: Exact Solutions. General Relativity and Gravitation, 34(11), pp. 1793-1818.

Edwards, C. H. & Penney, D. E., 2008.

Elementary Differential Equations. 6 ed. New Jersey: Pearson Education.

KBBI, 2016. Kamus Besar Bahasa Indonesia. [Online]

Available at: https://kbbi.kemdikbud.go.id/ [Accessed 25 April 2019].

Oxford, 2019. Oxford English Dictionary. [Online]

Available                                at:

https://en.oxforddictionaries.com/ [Accessed 27 April 2019].

Sabuwala, A. H. & Leon, D. D., 2011.

Particular Solution To The Euler–Cauchy Equation With Polynomial Non– Homogeneities. Discrete And Continuous Dynamical Systems, pp. 1271-1278.

Wright, C.,    1990. Wittgenstein on

Mathematical Proof. Royal Institute of Philosophy Supplement, Volume 28, pp. 79-99.

133