E-Jurnal Matematika Vol. 8(3), Agustus 2019, pp.246-252

DOI: https://doi.org/10.24843/MTK.2019.v08.i03.p260

ISSN: 2303-1751

PERHITUNGAN PREMI ASURANSI JOINT LIFE DENGAN MODEL VASICEK DAN CIR

I Made Wahyu Wiguna1§, Ketut Jayanegara 2, I Nyoman Widana3

§Corresponding Author

ABSTRACT

Premium is a sum of money that must be paid by insurance participants to insurance company, based on insurance contract. Premium payment are affected by interest rates. The interest rates change according to stochastic process. The purpose of this work is to calculate the price of joint life insurance premiums with Vasicek and CIR models. The price of a joint life insurance premium with Vasicek and CIR models, at the age of the insured 35 and 30 years has increased until the last year of the contract. The price of a joint life insurance premium with Vasicek model is more expensive than the premium price using CIR model.

Keywords: premium payments, interest rates, Vasicek and CIR.

  • 1. PENDAHULUAN

Secara konseptual asuransi merupakan pemindahan risiko dimana pihak tertanggung mengikatkan diri dalam bentuk kontrak polis kepada perusahaan asuransi Futami, (1993). Setiap peserta asuransi diwajibkan membayar premi kepada pihak perusahaan asuransi. Premi merupakan sejumlah uang yang wajib dibayarkan oleh peserta asuransi kepada perusahaan asuransi sesuai dengan kontrak yang telah disetujui.

Nilai premi bersih dipengaruhi oleh tingkat mortalitas dan tingkat suku bunga. Terdapat dua jenis suku bunga yaitu, suku bunga tetap dan suku bunga berubah secara tidak menentu (stokastik). Model tingkat suku bunga stokastik diantaranya menggunakan model Vasicek dan Cok Ingersol Ros (CIR).

Penelitian ini bertujuan menghitung nilai premi asuransi jiwa joint life dengan model Vasicek dan CIR. Peserta yang mengikuti asuransi yaitu dua orang berusia X dan y tahun dengan lama kontrak selama 10 tahun dan uang pertanggungan Rp. 100.000.000,00.

Menurut Futami (1993), tabel mortalitas merupakan tabel observasi mengenai peluang tingkat kematian berdasarkan kelompok umur. Fungsi-fungsi utama dalam tabel mortalitas adalah:

lχ+ι =  - dχ

_ dx =

Px=1-Qx

dengan lx merupakan banyaknya individu yang berhasil mencapai usia tepat X tahun, dx merupakan banyaknya individu yang meninggal antara umur X tahun sampai X+1 tahun, Qx merupakan  peluang individu  berumur  X

meninggal dalam kurun waktu 1 tahun, dan Px

merupakan  peluang individu  berumur  X

mencapai umur X+1 tahun.

Fungsi   gabungan yang  menyatakan

banyaknya orang berusia X tahun yang masih hidup dikalikan dengan banyaknya orang berumur y tahun yang masih hidup dinotasikan dengan ^xy . Peluang orang berusia x tahun dan y tahun akan tetap hidup selama 1 tahun dinotasikan dengan Pxy . Peluang orang berusia X tahun dan y tahun akan tetap hidup selama t tahun dinotasikan dengan tPxy dan dirumuskan sebagai berikut:

^xy =

lχ+l ly+1   lχy+l

Pxy =     ==

Lx Ly Lxy lχ+t ^y+tlχy+t

tPxy =        ==

l-x i-y

Peluang salah satu diantara X dan y meninggal dalam jangka waktu 1 tahun dinotasikan dengan tJxy dan dirumuskan sebagai berikut:

_ 1       _ ^χy - lχy+ι

fIxy=1-   =

fxy

Model Vasicek merupakan suatu model suku bunga stokastik yang mempunyai ciri khusus yaitu tingkat suku bunga akan cenderung kembali ke tingkat suku bunga rata-rata setelah mengalami penurunan atau peningkatan yang didefinisikan sebagai (Zeytun, 2007):

dr (t)=κ[θ-r(t)] dt + σdW(t),(1) r(0)= ⅞

Dengan    menggunakan    persamaan

differensial  parsial diperoleh solusi

persamaan (1) adalah:

r(t)=r0e kt +θ(1-e kt)

dari

(2)


+σ


∫

Jo


-k ( t-u ) dW (u)


Dari persamaan (2) di tentukan ekspektasi dan variansi yaitu (Bayazit, 2004)

E(r (t)) = r0e -kt + θ(1-е-kt )

Var(r (t)) = σ ( 1- e 2kt )    (3)

2k

Misalkan P^ (t) menyatakan ekspektasi dari nilai tunai pembayaran sebesar 1 unit pada saat t untuk tingkat suku bunga yang mengikuti model Vasicek Hull, (2003).

(B(')-‘)(β-2k2 )

σ2B(t) 2\

-r (0) B(t))(4)

4K/

Bi (t)=exp(


dengan ( t)=ι-eχp ( kt); B(t). Nilai awal pada tahap estimasi parameter didapatkan dari metode OLS(Ordinary Least Square). Metode OLS adalah metode estimasi dalam ilmu statistika yang meminimalkan jumlahan kuadrat dari eror. Persamaan (4) diubah menjadi bentuk

rt+ι - rt =(θ- rt)∆t+ CQ (5)

dengan εt ~N (0,1). Untuk menggunakan OLS, persamaan (5) ditranformasi ke bentuk:

rt+ι - rt = ∆t- Brt∆t+ σεt (6) dengan meminimalkan jumlahnya kuadrat dari bagian eror∑l=i ( ^, ^t )2 terhadap ̂ dan θ akan mendapatkan estimator untuk ̂ dan ̂ sebagai berikut:

n2-2n+l+U2U3-U1U3-(n-1) U4 (n2-2n+l-U3)∆t

(7)


̂


(n-1)U2-UjUi________

(n2-2n+l+U2U3-U1U3-(n-1) Uj )

(8)


dengan Ui =∑I=Ir t, U2 =∑1=1 rt+l,    =

∑1=1 r , dan U4 =∑i=i tv

Dan estimator untuk σ adalah Mariana dkk, (2015):

a=√n-2 ∑1=1 (( s √? -√ +Ǩ√r< ) (9)

Model CIR menjamin tingkat suku bunga bernilai positif dan memiliki sifat mean reversion atau mempunyai kecendrungan kembali menuju rata – rata. Bentuk dari model CIR adalah. Cox & Ross, (1985)

dr (t)=k(θ-r(t)) dt +σ√r(t) dW(t) (10)

Dengan menggunakan formula itu didapatkan penyelesaian model CIR sebagai berikut:

r(t+1)=θ(1-ek∆t)+e k∆  (t)

+∈(t+1)      (11)

dengan

e(t+1)=∫t+1σe k( t+i-u )

×√r(u) dW (u)

Setelah mendapatkan penyelesaian dari model CIR, selanjutnya dicari rata–rata dan varians. Dengan menghitung rata–rata model CIR, bisa dibuktikan sifat mean reversion dari model CIR. Rata–rata bisa didapat dengan menghitung ekspektasinya

E[r(t)]=e ktr(0)+θ(1-e kt)   (12)

Selanjutnya akan dihitung varians dari model CIR. Dengan terlebih dahulu menghitung E[ ^,2 (t)] dan (E[r(t)])2 maka bisa dihitung varians dari suku bunga model CIR.

Var (r(t))=E[ r2 (t)]-(E[r(t)])2

= (0)( ≤ )(e~kt - e 2kt)

+θ( I )(1-e kt)2 (13)

Sudah didapatkan penyelesaikan mean dan varians dari model CIR. misal P2 (t) menyatakan ekspetasi dari nilai tunai pembayaran sebesar 1 unit pada saat t untuk tingkat suku bunga yang mengikuti model CIR Hull, (2003).

2kθ

( t )        2d exp (2 t)     σ2

P2 (t)=(exp(td)(A:+d)+d-k )

× exp (- 2r (2 )(exp ( td )-1) )      (14)

∖ exp(td)(k+d)+d-k)

Nilai awal pada tahap estimasi parameter didapatkan dari metode OLS(Ordinary least square) persamaan (14) diubah menjadi bentuk:

rt+ι - rt =(θ- rt)∆t+σ√    (15)


Sebelum mencari nilai kappa, teta, dan zigma, terlebih dahulu mencari ∑t=ι rt ,  ∑t = l ,

∑ t = l t+1 , dan ∑ t = l rt + 1 sebagai berikut: rt 39


dengan εt ~N(0,1). Untuk menggunakan OLS, persamaan (15) ditransformasi ke bentuk:


∑ rt =   + T2+ ...+r39

t=l

= 0,06 + 0,065+ ... +0,0675


(rt+ι - rt )



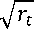
kθ∆ t

-k√ rt ∆t+ σεt (16)


39

∑ t=l


1

rt


= 2,85


1

=  +


11

r2        r39


Nilai tunai manfaat model Vasicek dan model CIR dihitung menggunakan persamaan sebagai berikut:

n-1

^xy: =∑P(k + 1)( kPxy - k+lPxy) (17) k=0


11   1

0,06 + 0,065+ ...+0,0675


= 16,66+15,38+⋯+14,81


= 535,3556

39


∑ n±ι

t=l l


Nilai tunai anuitas model Vasicek dan model


CIR dihitung menggunakan persamaan sebagai berikut:

̈ χy ∶ =∑k=θP(k) kPxy     (18)


=  + rl+⋯+ *40

rl r2        r39

0,065   0,065       0,065

= 0,06 + 0,065+⋯+0,075

= 1,08+1+⋯+0,96


= 39,09096

39


Perhitungan nilai Premi Asuransi Joint Life dengan Model Vasicek dan CIR dihitung


menggunakan persamaan sebagai berikut:


p   nxy: ̈ χy ∶


(19)


2. METODE PENELITIAN

Penelitian ini menentukan nilai premi asuransi jiwa joint life menggunakan tingkat suku bunga Vasicek dan CIR. Adapun langkah-langkah yang dilakukan dalam penelitian ini adalah:

  • 1.    Menentukan estimasi parameter untuk suku bunga Vasicek dan CIR

  • 2.    Menghitung suku bunga Vasicek dan CIR.

  • 3.    Membuat nilai tabel mortalitas joint life menggunakan Tabel Mortalitas Indonesia 2011.

  • 4.    Menghitung nilai premi Vasicek dan CIR pada asuransi joint life.

  • 5.    Menginterpretasikan hasil.


∑ rt+ι =   + T3+ ...+ ^40

t=l

= 0,065 + 0,065 + ⋯ + 0,065

= 2,855

Setelah memperoleh nilai tersebut, nilai kappa, teta, dan sigma dapat dihitung sebagai berikut:


K̂ = (402-2 .40+1+2,855 .535,3556

2,85 .535,3556-39 .39,09096)

1

×

(402+2 . 40+1-535,3556). 1

= 2,193516

-0,06424

θ = -0,87066

= 0,073778

σ = √ 1 (0,0658 + ⋯ + 0,078212)

38


= 0,325004


  • 3.    HASIL DAN PEMBAHASAN

    • 3.1    Estimasi Paramater Suku Bunga Vasicek

      dan CIR

Estimasi parameter suku bunga Vasicek dan CIR dicari menggunakan data suku bunga bulanan Bank Indonesia pada periode Juni 2013 - Juli 2016 seperti terlampir (Lampiran 1).


3.2 Menghitung Suku Bunga Vasicek dan CIR

Setelah memperoleh estimasi parameter dari suku bunga vasicek dan CIR, dilanjutkan dengan menghitung suku bunga vasicek dan CIR dengan menggunakan parameter yang sudah diperoleh sebelumnya, yaitu sebagai berikut: r(t)=r0e kt +θ (1 - e kt)


+σ∫te-k( t-u ) dW (U) r(1) = 0,065 . e-2, 193516 .1

+0,073778 (1

+0,325004 ∫

■'O

e-2,193516 .1)


-


1

e^2, 193516 . (I-U ) dW (U)


r(1) = 0,062863308

Selanjutnya, menghitung suku bunga CIR yaitu sebagai berikut:

r(t+1)= e k∆  (t)+θ (1 - e k∆t)

∫

σek( t+i-u)√ r(u)dW(u)

r (1) = e-2, 193516 .1 . 0,065

+0,073778 ( 1 - e^2, 193516 .1)

+∫ (0,325004 .e-2, 193516 (I-U)

■'O _______

×√r(u) dW (u)

= 0,06506093

hasil perhitungan disajikan pada tabel 1.

Tabel 1. Suku Bunga Vasicek dan CIR.

r(t)

Bunga Vasicek

Bunga CIR

1

0,062863308

0,06506093

2

0,075257336

0,073618098

3

0,076510695

0,074480968

4

0,064237383

0,071161118

5

0,068317996

0,072334078

6

0,070364989

0,072825063

7

0,070046763

0,07276794

8

0,074409478

0,074049469

9

0,072299374

0,073332396

10

0,075538539

0,074215606

(Sumber Data Diolah 2019)

  • 3.3    Tabel Perhitungan

Tabel 2. Perhitungan Single Life usia X = 35 sd 44 dan y = 30 sd 39 tahun

X

Q1

Px

y

Qy

Py

0

35

0.00091

0,99909

97389,85

30

0,00054

0,99946

98681,91

36

0.00099

0,99901

97301,22

31

0,00057

0,99943

98628,62

44

0,00279

0,99721

95897,39

39

0,00114

0,99886

97974,66

(Sumber: Biro Pusat Aktuaria)

Untuk mendapat nilai pada baris pertama Px dan Py , didapatkan dengan menggunakan persamaan Pzs = 1 - Q35 dan P30 = 1 - Q30, sehingga diperoleh nilai,

Px = 1 - 0,99909 = 0,00091. dan

Py = 1 - 0,99946 = 0,00054,

Selanjutnya dilanjutkan dengan membuat nilai tabel mortalitas joint life.

Tabel 3. Tabel Mortalitas Joint Life usia = 35 sd 44 dan y = 30 sd 39 tahun

(X,y)

Px ,y        \

cIx,y         \

(35,30)

0,99855

0,00145

(36,31)

0,998441

0,001559

(37,32)

0,998311

0,001689

(38,33)

0,998181

0,001819

(39,34)

0,998011

0,001989

.

.

.

(44,39)

0,996073

0,003927

(Sumber Data Diolah 2019)


Untuk mendapatkan nilai pada baris pertama yaitu,

,  =  0,99909 . 0,99946 = 0,99855

Q35 ,, 30 = 1-  P30,35 = 0,00145

Setelah melengkapi perhitungan tabel mortalitas joint life, dilakukan perhitungan premi asuransi joint life dengan tingkat suku bunga mengikuti model Vasicek dan CIR.

  • 3.4    Nilai Tunai Manfaat Model Vasicek dan

CIR

Nilai tunai manfaat model vasicek dihitung sebagai berikut:

n-1

^xy:    = ∑ Pvas (k + 1)( kPxy- k+lPxy)

k=0

^35 ,30:   =     (1)( 0^35,30 - 1^35,30)

+ Pvas(2)( 1P35,30 - 2P35,30)

+⋯+Pvas(10)( 9P35,30

  • -    lθP35,30)

= 0,93725323(1 - 0,99855049)

+ 0,87979054(0,99855049

–0,996993316+⋯

+0,53230018(0,98104953

- 0,977618367)

= 0,015271731

Nilai tunai manfaat model CIR sebagai berikut:

n-1

^xy:    = ∑ Pcir (k + 1)( kPxy - k+lPxy)

k=0

^35 ,30:   =    (1)( θP35,30 - 1P35,30)

+ Pcir(2)( 1P35,30 - 2P35,30)

+⋯+Pcir(10)( 9P35,30

  • -    lθP35,30)

= 0,932454057(1 - 0,998550491)

+0,867092258 - 0,996993316)

+⋯ +0,483618378(0,98104953

-0,977618367)

= 0,014488325

Untuk hasil perhitungan yang lebih lengkap disajikan pada tabel 4.

Tabel 4. Nilai Tunai Manfaat Model Vasicek dan CIR

x,y

A vasicek %y :

A CIR :

35,30

0.015271731

0.014488325

36,31

0.016883679

0.016010654

37,32

0.018754476

0.017777989

38,33

0.020926401

0.019830172

39,34

0.023458183

0.022224411

40,35

0.026362271

0.024972937

41,36

0.029677036

0.028111729

42,37

0.033413809

0.031648927

43,38

0.037631351

0.035641468

44,39

0.042369949

0.040131303

(Sumber Data Diolah 2019)

  • 3.5    Nilai Tunai Anuitas Model Vasicek dan

CIR

Nilai tunai anuitas model vasicek dihitung sebagai berikut:

n-1

̈ xy ∶       =∑Pvas (k) kPxy

k=0

̈35,30∶      =     (0) 0^35,30 + Pvas (1) 1P35,30

+⋯+Pvas (9) 9P35,30

= 1 × 1 + 0,93725323

× 0,998550491 + ⋯ +0,5668016 × 0,98104953 = 7,589956343

Selanjutnya dihitung nilai tunai anuitas model CIR sebagai berikut:

n-1

̈ xy ∶    =∑P(k) kPxy

k=0

̈35,30∶   =     (0) θP35,30 + Pcir (1) 1P35,30

+⋯+Pcir (9) 9P35,30

= 1 × 1 + 0,932454057

× 0,998550491 + ⋯

+0,520235652 × 0,98104953

= 7,328968194

Untuk hasil perhitungan yang lebih lengkap disajikan pada tabel 5.

Tabel 5. Nilai Tunai Anuitas Model Vasicek dan CIR

x,y

̈                                                             , ∶

̈ CIR x,y∶

35,30

7.589956343

7.328968194

36,31

7.584685159

7.324004023

37,32

7.578521414

7.31819869

38,33

7.571337682

7.311431927

39,34

7.56280898

7.303393255

40,35

7.552848908

7.294001673

41,36

7.541355564

7.283160921

42,37

7.5284848

7.271024655

43,38

7.513924723

7.25729747

44,39

7.49722236

7,26044119

(Sumber Data Diolah 2019)

  • 3.6    Perhitungan Premi Asuransi Joint Life dengan Model Vasicek dan CIR.

Perhitungan nilai premi asuransi joint life

model vasicek pertanggungan


dan CIR dengan uang Rp. 100.000.000,00 dihitung

menggunakan persamaan sebagai berikut:

p

rv as


χy : . 100000000

Cl ■xy ∶

=    , 30:   . 100000000

̈ •35 ,30∶

0.014488325

=7.589956343. 100000000

= Rp. 201.210,00

41

Pcir = lχy : . 100000000

Cl ■xy ∶

A1

ττ^ , 30:   .100000000

̈ •35 ,30∶

0.014488325

7.328968194


. 100000000


= Rp. 197.686,00

Sehingga diperoleh hasil perhitungannya disajikan pada tabel 6.

Tabel 6. Premi Asuransi Joint Life dengan Model Vasicek dan CIR.

x,y

Premi Vasicek

Premi CIR

35,30

Rp

201.209,00

Rp

197.685,00

36,31

Rp

222.602,00

Rp

218.605,00

37,32

Rp

247.468,00

Rp

242.928,00

38,33

Rp

276.389,00

Rp

271.221,00

39,34

Rp

310.178,00

Rp

304.302,00

40,35

Rp

349.037,00

Rp

342.376,00

41,36

Rp

393.523,00

Rp

385.982,00

42,37

Rp

443.831,00

Rp

435.274,00

43,38

Rp

500.821,00

Rp

491.112,00

44,39

Rp

565.142,00

Rp

554.181,00

(Sumber Data Diolah 2019)

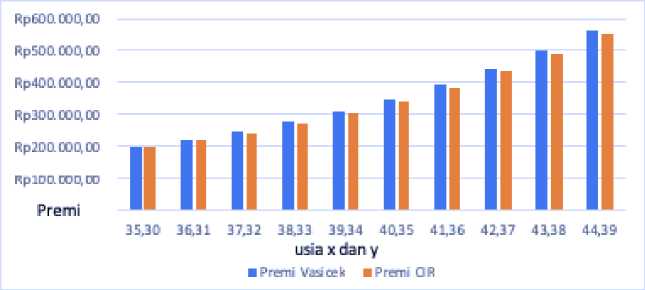
Gambar 1. Perbandingan nilai premi Vasicek dan CIR.


Untuk melihat lebih jelas hasil pada tabel 6, disajikan dalam bentuk grafik pada gambar 1. Gambar 1 menunjukan bahwa nilai premi asuransi jiwa joint life dengan usia tertanggung 35 tahun dan 30 tahun dengan lamanya kontrak 10 tahun menggunakan model Vasicek dan CIR mengalami peningkatan hingga akhir tahun kontrak, dan diketahui bahwa model Vasicek lebih mahal dari CIR.

  • 4. SIMPULAN DAN SARAN

Berdasarkan kontrak dalam penelitian ini, nilai premi asuransi jiwa joint life dengan usia tertanggung X = 35 dan y = 30 tahun dengan

DAFTAR PUSTAKA

Bayazit, D. 2004. Yield Curve Estimation and Prediction with Vasicek Model. The Midldle East Technical University, Ankara.

Cox J. C., Ingersoll J. E., and Ross S. A. 1985. “A Theory of The Term Structure of Interest Rates”. Econometrica Vol. 53, Issue 2, pp.385-408.

Futami, T. (1993). Matematika Asuransi Jiwa, Bagian I. Tokyo: Oriental Life Insurance Cultural Development Center.

lamanya kontrak 10 tahun dengan uang pertanggungan rp.100.000.000,00, menggunakan model Vasicek adalah Rp. 201.210,00 sedangkan dengan model CIR adalah sebesar Rp.197.686,00. Nilai premi asuransi jiwa joint life dengan menggunakan model Vasicek relatif lebih mahal dibandingkan dengan harga premi asuransi jiwa joint life dengan menggunakan model CIR.

Disarankan untuk penelitian selanjutnya dapat menghitung nilai premi produk asuransi dengan model tingkat suku bunga yang berbeda dan juga diharapkan dapat memperhitungkan faktor biayanya dalam menghitung premi.

Hull, J.C. 2003. Option, Future, and Other Derivatives. USA: Prentice Hall.

Mariana, E., Erna, A., & Sentot, D, S. 2015. “Estimasi Parameter pada Model Suku Bunga Cox  Ingersoll  Ross  (CIR)

Menggunakan  Kalman  Filter  untuk

Menentukan Harga Zero Coupon Bond”. Jurnal Sains dan Seni, ITS.Surabaya: FIMPA Institut Teknologi Sepuluh Nopember.

Zeytun, S., 2007. A Comparative Study of the Vasicek and the CIR Model of the Short Rate. Germany: Fraunhofer: Institut fur Techno- und Wirtschaftsmathematik.

Lampiran 1. Estimasi Parameter Suku Bunga Bank Indonesia

Tanggal

Bunga

Bunga (Tt)

t

r( t+1 )

1/Tt

r(t+ι∙)∕rt

((T( t+ι)→"t)∕sqrt(Tt) - teta∕sqrt(rt) + K*sqrt( t))^2

13-Jun-13

6,00%

0,06

1

0,065

16,666667

1,083333

0,065799097

11-Jul-13

6,50%

0,065

2

0,065

15,384615

1

0,072822709

15-Agu-13

6,50%

0,065

3

0,07

15,384615

1,076923

0,08379198

29-Agu-13

7,00%

0,07

4

0,0725

14,285714

1,035714

0,096685686

12-Sep-13

7,25%

0,0725

5

0,0725

13,793103

1

0,100246084

08-Okt-13

7,25%

0,0725

6

0,075

13,793103

1,034483

0,106211714

12-Nov-13

7,50%

0,075

7

0,075

13,333333

1

0,10977223

12-Des-13

7,50%

0,075

8

0,075

13,333333

1

0,10977223

09-Jan-14

7,50%

0,075

9

0,075

13,333333

1

0,10977223

13-Feb-14

7,50%

0,075

10

0,075

13,333333

1

0,10977223

13-Mar-14

7,50%

0,075

11

0,075

13,333333

1

0,10977223

08-Apr-14

7,50%

0,075

12

0,075

13,333333

1

0,10977223

08-Mei-14

7,50%

0,075

13

0,075

13,333333

1

0,10977223

12-Jun-14

7,50%

0,075

14

0,075

13,333333

1

0,10977223

10-Jul-14

7,50%

0,075

15

0,075

13,333333

1

0,10977223

14-Agu-14

7,50%

0,075

16

0,075

13,333333

1

0,10977223

11-Sep-14

7,50%

0,075

17

0,075

13,333333

1

0,10977223

07-Okt-14

7,50%

0,075

18

0,075

13,333333

1

0,10977223

13-Nov-14

7,50%

0,075

19

0,0775

13,333333

1,033333

0,115904591

18-Nov-14

7,75%

0,0775

20

0,0775

12,903226

1

0,119459836

11-Des-14

7,75%

0,0775

21

0,0775

12,903226

1

0,119459836

15-Jan-15

7,75%

0,0775

22

0,075

12,903226

0,967742

0,11333279

17-Feb-15

7,50%

0,075

23

0,075

13,333333

1

0,10977223

17-Mar-15

7,50%

0,075

24

0,075

13,333333

1

0,10977223

14-Apr-15

7,50%

0,075

25

0,075

13,333333

1

0,10977223

19-Mei-15

7,50%

0,075

26

0,075

13,333333

1

0,10977223

18-Jun-15

7,50%

0,075

27

0,075

13,333333

1

0,10977223

14-Jul-15

7,50%

0,075

28

0,075

13,333333

1

0,10977223

18-Agu-15

7,50%

0,075

29

0,075

13,333333

1

0,10977223

17-Sep-15

7,50%

0,075

30

0,075

13,333333

1

0,10977223

15-Okt-15

7,50%

0,075

31

0,075

13,333333

1

0,10977223

17-Nov-15

7,50%

0,075

32

0,075

13,333333

1

0,10977223

17-Des-15

7,50%

0,075

33

0,0725

13,333333

0,966667

0,103806535

14-Jan-16

7,25%

0,0725

34

0,07

13,793103

0,965517

0,094452868

18-Feb-16

7,00%

0,07

35

0,0675

14,285714

0,964286

0,08529028

17-Mar-16

6,75%

0,0675

36

0,0675

14,814815

1

0,081749933

21-Apr-16

6,75%

0,0675

37

0,0675

14,814815

1

0,081749933

19-Mei-16

6,75%

0,0675

38

0,0675

14,814815

1

0,081749933

16-Jun-16

6,75%

0,0675

39

0,065

14,814815

0,962963

0,076340004

21-Jul-16

6,50%

0,065

40

0

15,384615

0

0,000222185

252