PEMODELAN JUMLAH KASUS PNEUMONIA BALITA DI JAWA TIMUR MENGGUNAKAN REGRESI SPATIAL AUTOREGRESSIVE MOVING AVERAGE
on
E-Jurnal Matematika Vol. 8(3), Agustus 2019, pp.236-245
DOI: https://doi.org/10.24843/MTK.2019.v08.i03.p259
ISSN: 2303-1751
PEMODELAN JUMLAH KASUS PNEUMONIA BALITA DI JAWA TIMUR MENGGUNAKAN REGRESI SPATIAL AUTOREGRESSIVE MOVING AVERAGE
Made Narymurti Widyastuti1§, I Gusti Ayu Made Srinadi2, Made Susilawati3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: nary.widyastuti@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@gmail.com] §Corresponding Author
ABSTRACT
The purpose of this study is to model and determine the factors that significantly influence the number of toddler pneumonia cases in East Java Province. Modeling the number of toddler pneumonia cases was conducted using spatial autoregressive moving average (SARMA) regression analysis. The results showed that the best model to modeling was SARMA (1.1) with the AIC value is 649,55 and the coefficient of determination (R2) is 73,17%. The significant factors that affect the number of these cases are the number of toddler receiving complete basic immunization and the number of toddler receiving health services in each district/city.
Keywords: Regression, SARMA, toddlers Pneumonia case
Analisis regresi spasial adalah metode statistika untuk data yang memiliki pengaruh lokasi atau daerah. Analisis terhadap data seperti ini memerlukan perhatian khusus karena kondisi dari suatu lokasi pengamatan berbeda dengan lokasi pengamatan lain. Meskipun demikian, sesuai dengan hukum pertama geografis yang dikemukakan oleh Tobler kondisi di suatu lokasi pengamatan memiliki hubungan yang erat dengan lokasi pengamatan lain yang berdekatan (Anselin, 1988).
Pemodelan spasial dapat dibedakan menjadi dua yaitu pemodelan dengan tipe data berdasarkan pendekatan titik dan tipe data berdasarkan pendekatan area. Selain itu, dikembangkan analisis spasial dengan pengaruh spasial pada tingkat yang lebih tinggi yaitu spatial autoregressive moving average (SARMA). Model SARMA memiliki struktur yang dibangun melalui model deret waktu ARMA. Dalam model SARMA terdapat matriks pembobot spasial sebagai pengganti pengaruh waktu pada model deret waktu ARMA. Menurut Kruk (2002) kelebihan dari model ini adalah parameter model spasial dapat diestimasi untuk hubungan spasial pada tingkatan yang lebih tinggi.
Di Provinsi Jawa Timur pneumonia pada balita masih menjadi masalah kesehatan yang cukup besar. Pada tahun 2017 kasus pneumonia di Provinsi Jawa Timur mencapai 86.358 balita penderita ditemukan dan ditangani. Walaupun jumlah ini menurun dari tahun sebelumnya (tahun 2016 mencapai 102.712), kasus pneumonia balita di Provinsi Jawa Timur masih tinggi.
Tingginya jumlah kasus pneumonia balita ini berdampak buruk bagi kualitas kesehatan. Oleh karena itu, untuk menanggulangi hal ini dilakukan analisis guna meminimalkan jumlah kasus tersebut. Penularan penyakit serta peningkatan frekuensi infeksi pneumonia balita menurut Qaulyiah (2010) dipengaruhi oleh letak geografis. Oleh karena itu analisis dilakukan dengan analisis regresi SARMA untuk memodelkan kasus pneumonia pada setiap kabupaten/kota di Provinsi Jawa Timur. Tujuan dari penelitian ini adalah untuk memodelkan jumlah kasus pneumonia di setiap kabupaten/kota di Provinsi Jawa Timur serta untuk mengetahui faktor yang secara signifikan berpengaruh terhadap jumlah kasus pneumonia balita di Provinsi Jawa Timur.
Data pada penelitian ini berupa data sekunder yang diperoleh dari Profil Kesehatan Dinas Kesehatan Provinsi Jawa Timur. Unit observasi (amatan) penelitian ini adalah data profil kesehatan pada 38 kabupaten/kota di Provinsi Jawa Timur pada tahun 2017. Varibel dependen penelitian ini adalah jumlah kasus pneumonia balita di setiap kabupaten/kota di Provinsi Jawa Timur ( K) .Variabel independen terdiri dari jumlah balita yang mendapat ASI eksklusif (X1), jumlah balita yang mendapat imunisasi dasar lengkap (X2 ), jumlah balita yang mendapatkan pelayanan kesehatan (X3 ), jumlah rumah tangga ber-PHBS (X4), dan jumlah penduduk miskin (X5) di setiap kabupaten/kota di Provinsi Jawa Timur.
Metode analisis yang digunakan pada penelitian ini adalah analisis regresi spasial autoregresive moving average (SARMA), dengan tahapan analisis sebagai berikut:
-
1. Estimasi Model Regresi Linier dan Uji
Asumsi Regresi Linier
Analisis regresi merupakan metode statistika yang memanfaatkan hubungan antar dua variabel sehingga salah satunya dapat diramalkan dari variabel lainnya. Model umum dari analisis regresi dapat dinyatakan sebagai berikut (Kutner, et al., 2005).
Yt = βo + 1x^1, 1 +-----+ βk - 1 Xi, k - 1 + £(■ (1)
Model regresi linier sederhana yang merupakan landasan dari banyak teori ekonometrika memiliki beberapa asumsi (Gujarati & Porter, 2009), diantaranya yaitu: a. Varians dari galat adalah konstan atau homoskedastisitas.
Menurut Gujarati & Porter (2009), salah satu uji formal yang dapat dilakukan untuk mengidentifikasi homokedastisitas adalah uji Bruesch-Pagan. Hipotesis dari uji ini adalah sebagai berikut:
H0 : Ragam homogen
H1 : Ragam tidak homogen
Keputusan penolakan adalah ketika
nilai B >>^κ _ i )2.
-
b. Tidak terdapat autokorelasi antarsisaan.
Mengidentifikasi adanya autokorelasi dapat dilakukan dengan uji Durbin-Watson.
Hipotesis dari uji ini adalah sebagai berikut:
H0 : Tidak terdapat autokorelasi
H1 : Terdapat autokorelasi
Nilai statistik uji Durbin-Watson ( d)
dibandingkan dengan nilai dan
pada tabel Durbin-Watson. Daerah kritis didefinisikan sebagai berikut:
-
- jika d < dL maka H0 ditolak yang artinya terdapat autokorelasi;
-
- jika > maka tidak dapat
-
d itolak yang artinya tidak terdapat autokorelasi;
-
- jika LL < d ≤ dU maka pengujian tidak meyakinkan.
-
c. Tidak terdapat multikolinieritas, artinya tidak terdapat hubungan linier yang sempurna antar variabel bebas.
Multikolinieritas pada suatu model regresi linier diidentifikasi dengan menghitung nilai variance-inflating factor (VIF). Nilai VIF yang kurang dari lima menunjukkan bahwa tidak terdapat multikolinieritas pada model.
-
d. Sisaan dari model yang diestimasi
berdistribusi normal.
Kenormalan sisaan dari suatu model dapat diketahui dengan melakukan uji Jarque-Bera. Hipotesis dari uji ini adalah sebagai berikut:
H0 : Sisaan mengikuti sebaran normal H1 : Sisaan tidak mengikuti sebaran normal
Uji Jarque-Bera mempunyai distribusi chisquare dengan derajat bebas 2. Jika JP > x2 maka H0 ditolak yang artinya sisaan dari model tidak berdistribusi normal.
-
2. Uji Kebergantungan Spasial
Regresi spasial merupakan metode statistika yang digunakan untuk menganalisis hubungan antara variabel dependen dan independen dengan mempertimbangkan pengaruh antar daerah. Model regresi spasial secara umum dapat dinyatakan sebagai berikut (Anselin, 1988).
y = φW1+Xl+ + ΘW2+ + μ. (2)
Matriks W1 sama dengan W2 yang sering disebut matriks pembobot spasial (W). Matriks ini berupa matriks simetris berukuran n × n yang menunjukan hubungan kedekatan antar wilayah. Struktur yang mendasari hubungan kedekatan antar wilayah adalah bahwa jika dua daerah yang memiliki batas umum dengan panjang tidak-nol, daerah ini dianggap berdekatan dan nilai bobotnya adalah satu, jika tidak makan nilai bobotnya adalah nol.
Terdapat pengembangan regresi spasial pada tingkat yang lebih tinggi yaitu spatial autoregressive moving average (SARMA). SARMA merupakan analisis spasial yang mengasumsikan bahwa terdapat pengaruh spasial pada variabel dependen dan sisaan. Model SARMA merupakan analogi spasial dari kelas model deret waktu ARMA yang dengan matriks pembobot spasial sebagai pengganti faktor waktu dalam model deret waktu ARMA.
Model SARMA dikembangkan menjadi model regresi SARMA yang ditandai dengan penambahan variabel independen pada model SARMA. Model regresi SARMA secara umum adalah sebagai berikut:
n
n
Vi = + Φι ∑ Wi , jyj+⋯+Φp ∑ ,
7 = 1
7 = 1
+ βlXl,i+⋯+βk-Λ-l,i n
(3)
+ 01 ∑ Wi ,jzi+⋯
J = I n
+ θq ∑ W! , 'iεi + ?i .
J=I
Bila dinotasikan dengan matriks, Persamaan (3) dapat dinyatakan sebagai berikut.
(ι-∑φiWi)y= +('+∑ θiWi)ε . (4)
Matriks W merupakan matriks simetris, sehingga dapat didiagonalisasi. Oleh karena itu dapat dibentuk matriks orthogonal U dan V yang memenuhi W= AV, dengan V = U = U1 , Ʌ menyatakan dicιc∣ ( ^-I ,A 2,… ,λn ) dan An merupakan nilai eigen dari matriks W. Berdasarkan hal tersebut, Persamaan (4) dapat dinyatakan sebagai berikut:
U (' -∑ΦiΛ)Vy= + U (' +∑Oi Λ)Vε. (5)
misalkan:
Ω1
Ω2
=('-∑φtΛ ' ), ÷∑ *Λ ' ),
Α=UΩ1 V,
B=UΩ2 V.
Sehingga Persamaan (5) dapat dinyatakan
sebagai berikut:
Ay = + Bε
ε= (Ay - Xβ).
(6)
ε berdistribusi normal, sehingga dapat dibentuk fungsi densitas peluang sebagai berikut:
f( Zi)=√2πσ2eXP [-2 σ2 ( ε∙2 )].(7)
Fungsi likelihood dari fungsi densitas peluang
pada Persamaan (7) adalah sebagai berikut: n
L( Zi , ”2)=(2πσ2 ) 2 exp{-2 1(λ )}.(8)
Logaritma natural dari Persamaan (8) adalah
sebagai berikut:
ln(L)=- ln(2π)- ln(σ2)+ln|B~1A |
+[-2σ2 ( B-^ ( Ay
- Xβ))τB~1 ( Ay - Xβ)]. (9) diperhatikan bahwa
ln|B~1A | = ln(|UΩ21VUΩ1v|) (10)
= ln(| ||ΩΞ1ΩiIlVl)
=ln(|U||ΩΞ1Ωi||1 |)
= ln|Ω21Ω1|
=ln
(' +∑ *Λ ' ) ('
-
n
=∑ln i=i
∑ φt Λ • )|
(1-∑1J=M ) (1+∑cJ=M).
Dengan mensubstitusikan Persamaan (10) ke Persamaan (9), diperoleh fungsi logaritma natural (In) likelihood sebagai berikut: n
ln(L)=- In(2π)-?'n(σ2)+∑In(9i ) 22
1 +[-2σ2 ( s- ( Ay
- Xβ))τB~1( Ay - Xβ)]. (11)
(i-∑j=ι Φjλi ) 1
dengan 9i = dan Ω2 1Ω=
dia,Q (9i, 92,…,9n).
Penduga parameter model regresi SARMA terdiri dari:
-
a. Penduga Parameter β
Pendugaan parameter β diperoleh dengan menurunkan fungsi ln likelihood pada
Persamaan (10) secara parsial terhadap β dan menyatakannya dengan nol. Penduga parameternya adalah sebagai berikut:
̂=(xτ(̂ ̂τ) 1X)~1χτ(̂ ̂τ) ̂y (12)
-
b. Penduga Parameter σ2
Pendugaan parameter σ2 diperoleh dengan menurunkan fungsi ln likelihood pada Persamaan (11) secara parsial terhadap σ2 dan menyatakannya dengan nol, sehingga diperoleh penduga parameternya sebagai berikut:
̂2 =1( ∕ ̂y)τM∕̂y (13)
n
-
c. Penduga Parameter Φ dan θ
Pendugaan parameter Φ dan θ tidak dapat dilakukan dengan dilakukan dengan menurunkan fungsi ln likelihood (metode maximum likelihood estimator) (Huang, 1984). Oleh karena itu diperlukan metode iterasi dalam menduga parameternya. Metode iterasi yang digunakan adalah iterasi numerik Davidon-Fletcher-Powell.
Adanya kebergantungan spasial pada data dapat diketahui dengan melakukan uji Lagrange Multiplier (LM). Terdapat tiga jenis uji Lagrange Multiplier (LM), antara lain: a. uji kebergantungan spasial pada variabel
dependen;
-
b. uji kebergantungan spasial pada sisaan;
-
c. uji kebergantungan spasial pada variabel dependen dan sisaan.
-
3. Pemodelan regresi spatial autoregressive moving average (SARMA)
Setelah itu, data yang memiliki kebergantungan spasial pada variabel dependen dan sisaan dianalisis dengan analisis regresi (SARMA). Pertama dilakukan penentuan model SARMA dengan fungsi autokorelasi spasial, selanjutnya menduga parameter model regresi SARMA yang diidentifikasi, memilih model terbaik dari model yang diidentifikasi dengan kriteria nilai AIC, melakukan uji signifikansi pada parameter model yang terpilih, dan terakhir interpretasi pada model terbaik.
Deskripsi Jumlah Kasus Pneumonia Balita di Provinsi Jawa Timur serta Faktor yang Memengaruhinya
Angka yang menunjukkan banyaknya kasus dari setiap variabel dalam penelitian ini tampilkan dalam peta tematik (terlampir), hal ini bertujuan untuk mengetahui penyebaran data dari setiap variabel dari sudut kewilayahan. Dalam peta tematik banyaknya
kasus dari setiap variabel dikelompokan menjadi lima kategori yaitu sangat rendah, rendah, sedang, tinggi, dan sangat tinggi.
Pada Lampiran 1 menampilkan pembagian wilayah Provinsi Jawa Timur dengan keterangan warna yang berbeda di setiap Kabupaten/Kota, sedangkan pada lampiran 2 menampilkan gambar peta tematik dari setiap variabel penelitian. Peta tematik pada Lampiran 2 menunjukkan bahwa warna lokasi semakin gelap mengidentifikasikan penyebaran jumlah kasus semakin tinggi.
-
- Kabupaten/kota yang masuk dalam kategori jumlah kasus pneumonia balita sangat tinggi adalah Kabupaten Gresik dan Sidoarjo (Gambar 2(a)).
-
- Kategori jumlah balita yang mendapat ASI eksklusif sangat rendah ada pada Kabupaten Lamongan, Kota Probolinggo, Kota Malang, Kota Madiun, Kabupaten Lumajang, Kota Blitar, Kota Mojokerto, Kota Pasuruan, Kota Kediri, dan Kota Batu (Gambar 2(b)).
-
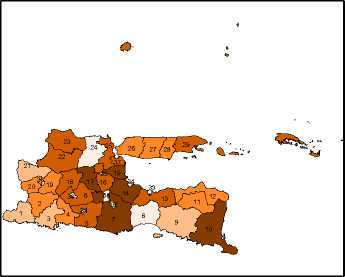
- Kabupaten/kota yang masuk dalam kategori jumlah balita yang mendapat imunisasi dasar lengkap sangat rendah adalah Kabupaten Probolinggo, Kota Mojokerto, Kota Blitar, Kabupaten Kediri, Kota Madiun, Kota Batu, Kota Pasuruan, Kabupaten Malang, Kota Probolinggo, Kota Kediri, dan Kabupaten Pacitan (Gambar 2(c)).
-
- Kabupaten/kota yang masuk dalam kategori jumlah balita yang mendapatkan pelayanan kesehatan sangat tinggi adalah Kabupaten Sidoarjo, Kabupaten Jember, Kabupaten Malang, dan Kabupaten Surabaya (Gambar 2(d)).
-
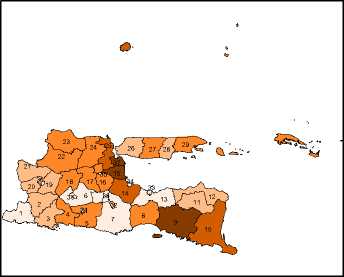
- Kabupaten/kota yang masuk dalam kategori jumlah rumah tangga ber-PHBS sangat rendah adalah Kota Batu, Kabupaten Blitar, Kabupaten Pacitan, Kota Blitar, Kota Pasuruan, Kabupaten Malang, Kota Mojokerto, Kabupaten Sumenep, Kabupaten Kediri, Kota Blitar, Kabupaten Blitar, Kabupaten Situbondo, Kota Lumajang, Kota Kediri, dan Kabupaten Sampang (Gambar 2(e)).
-
- Kabupaten/kota yang masuk dalam kategori jumlah penduduk miskin sangat tinggi adalah Kabupaten Sampang, Kabupaten Probolinggo, Kabupaten Jember, dan Kabupaten Malang (Gambar 2(f)).
Estimasi Model Regresi Linier dan Uji
Asumsi Analisis Regresi Linier
Estimasi parameter model regresi linier dari penelitian ini adalah sebagai berikut:
Tabel 1. Estimasi Parameter Model Regresi
|
Estimasi Parameter |
Standar Eror |
^hitung |
p l value | |
|
β0 |
361,032509 |
438,09472 |
0,824 |
0,4160 |
|
βl |
0,032430 |
0,046397 |
0,699 |
0,4896 |
|
β2 |
0,084991 |
0,032475 |
2,617 |
0,0134 |
|
β3 |
0,020332 |
0,009613 |
2,115 |
0,0423 |
|
β4 |
0,002648 |
0,003903 |
0,679 |
0,5023 |
|
β- |
-0,004027 |
0,004147 |
-0,971 |
0,3388 |
|
R2 = 59,07% | ||||
Sumber: data diolah, 2019
Estimasi model regresi linier pada Tabel 1 berdasarkan pada variabel X yang signifikan berpengaruh, yaitu variabel X yang mempunyai nilai P lebih kecil dari α=0,05. Estimasi model regresi dapat dituliskan sebagai berikut:
̂ = 361,032509 + 0,084991 , + 0,020332 , ,. (14)
Hasil pengujian asumsi analisis regresi linier pada Persamaan 14, dengan menggunakan software R diperoleh sebagai berikut:
Tabel 2. Uji Asumsi Analisis Regresi Linier
|
Hipotesis Uji |
Statistik Uji |
Keputusan |
|
Hq= Sisaan mengikuti sebaran normal Hγ= sisaan tidak mengikuti sebaran normal |
Z2=5,866 df=2 p-value=0,05324 Z(0.05)3= 5,991 |
Hq diterima. Hal ini berarti sisaan pada model mengikuti sebaran normal. |
|
H0 = tidak terdapat autokorelasi H-^= terdapat autokorelasi |
DW =1,6286 dL =1,2042 dU =1,7916 dl < DW < dU \ |
Pengujian tidak meyakinkan. Ada indikasi bahwa terdapat autokorelasi. |
|
Hq = ragam homogen H-^ = ragam tidak homogen |
BP = 14,241 df = 5 p-value= 0,01412 Z(0.1)5= 11,070 |
H0 ditolak. Hal ini berarti ragam pada model tidak homogen. |
Sumber: data diolah, 2019
Tabel 3. Uji Multikolinieritas
|
Variabel |
Nilai VIF |
Keputusan |
|
*1 |
2,232909 |
Tidak terdapat multikolinieritas |
|
X2 |
1,966625 | |
|
X3 |
2,904407 | |
|
X4 |
1,538612 | |
|
X5 |
2,216688 |
Sumber: data diolah, 2019
Tabel 3 menunjukkan bahwa tidak terdapat multikolinieritas pada model karena nilai VIF dari masing-masing variabel kurang dari lima. Pada Tabel 2 terlihat bahwa masih terdapat pelanggaran asumsi dari uji asumsi analisis regresi linier yang dilakukan. Pada uji homoskedastisitas hasil yang diperoleh adalah ragam tidak homogen dan pada uji autokorelasi hasil yang diperoleh tidak meyakinkan, sehingga ada indikasi bahwa terdapat autokorelasi pada model. Oleh karena itu model regresi linier pada Persamaan 14 kurang baik untuk digunakan. Karena model yang diperoleh kurang baik, terdapat indikasi/kemungkinan adanya pengaruh spaisal pada data yang dianalisis. Untuk mengetahui hal tersebut, analisis dilanjutkan dengan uji kebergantungan spasial guna melihat ada tidaknya pengaruh spasial pada data yang digunakan.
Uji Kebergantungan Spasial
Kebergantungan spasial pada data dapat diketahui dengan melakukan uji Lagrange Multiplier. Hasil uji diperoleh sebagai berikut:
Tabel 4. Uji Lagrange Multiplier
|
Hipotesis |
Nilai Statisti Uji |
Keputusan |
|
H0 : =0 Hi : ≠0 |
LMlag = 0,1663 Z(0.1)5 = 3,841 P- = 0,68342 |
Hq diterima. Tidak terdapat kebergantungan spasial pada variabel dependen. |
|
H0 : =0 Hi : ≠0 |
= 1,4114 Z(0.1)5 = 3,841 P- = 0,23483 |
Hq diterima. Tidak terdapat kebergantungan spasial pada sisaan. |
|
H0 : =0 dan θ =0 Hi : ≠0 dan : θ≠0 |
^lag ,err = 6,796 Z(0.1)5 = 5,991 P- = 0,03344 |
H0 ditolak. Terdapat kebergantungan spasial pada variabel dependen dan sisaan. |
Sumber: data diolah, 2019
Hasil uji Lagrange Multiplier pada Tabel 4 menunjukkan bahwa terdapat kebergantungan spasial pada variabel dependen dan sisaan sehingga analisis dilanjutkan dengan model analisis regresi spatial autoregressive moving average (SARMA).
Fungsi Autokorelasi Spasial
Untuk mengidentifikasi model yang tepat dalam pendugaan model SARMA digunakan
fungsi autokorelasi (ACF) seperti halnya pada model ARMA. Fungsi autokorelasi spasial menunjukkan kekuatan autokorelasi spasial dari unit spasial pada tingkat tertentu.
Tabel 5. Uji Signifikansi ACF
|
Koefisien |
Selang (Interval) | |
|
Autokorelasi Pada Variabel Dependen | ||
|
1 |
0,3614708 |
(0,08731657; 0,635625) |
|
2 |
-0,02107975 |
(-0,295234; 0,2530744) |
|
3 |
-0,09034016 |
(-0,3644944; 0,183814) |
|
4 |
-0,09292131 |
(-0,3670755; 0,181233) |
|
5 |
-0,05388414 |
(-0,3280383; 0,220270) |
|
6 |
-0,06880983 |
(-0,342964; 0,2053444) |
|
7 |
-0,05341103 |
(-0,327565; 0,2207432) |
|
Autokorelasi Pada Sisaan | ||
|
1 |
-0,1660659 |
(-0,440220; 0,1080883) |
|
2 |
0,0127776 |
(-0,261377; 0,2869318) |
|
3 |
-0,06905472 |
(-0,343209; 0,2050995) |
|
4 |
-0,1230305 |
(-0,97185; 0,1511237) |
|
5 |
0,02602153 |
(-0,248133; 0,3001757) |
|
6 |
0,01401625 |
(-0,260138; 0,2881705) |
|
7 |
0,00316206 |
(-0,270992; 0,2773163) |
Sumber: data diolah, 2019
Hasil Uji signifikansi koefisien autokorelasi pada Tabel 5 menunjukkan bahwa koefisien autokorelasi signifikan pada fungsi autokorelasi variabel dependen order (tingkat) pertama karena interval pada koefisien autokorelasi tersebut tidak memuat nilai 0, sehingga pemodelan regresi SARMA yang akan dilakukan adalah pemodelan regresi SARMA pada tingkat pertama.
Pemodelan Regresi Spatial Autoregressive Moving Average (SARMA)
Model regresi SARMA pada tingkat pertama terdiri dari SARMA (1,0), SARMA (0,1), dan SARMA (1,1). Penduga parameter dari masing–masing model regresi SARMA tersebut adalah sebagai berikut:
Tabel 6. Penduga Parameter Regresi SARMA
|
Penduga Parameter | |||
|
SARMA (1,0) |
SARMA (0,1) |
SARMA (1,1) | |
|
βn |
240,69631 |
252,18542 |
-144,89 |
|
β, |
0,0304212 |
0,0421493 |
-0,02097 |
|
β2 |
0,0819201 |
0,0920442 |
0,09932 |
|
β3 |
0,0194716 |
0,0273765 |
0,02247 |
|
β4 |
0,0024479 |
0,0041200 |
0,00122 |
|
β. |
-0,0034122 |
-0,0075780 |
-0,00472 |
|
Φl |
0,057329 |
0,08332 | |
|
θ1 |
-0,38079 |
-0,63415 | |
|
R2 |
59,27% |
62,99% |
73,17% |
Sumber: data diolah, 2019
Untuk menentukan model terbaik, dilakukan dengan melihat nilai Akaike’s Information Criterion (AIC) pada masing-masing model. Nilai AIC dari masing-masing model adalah sebagai berikut.
Tabel 7. Nilai AIC Model Regresi SARMA
|
Nilai AIC | |
|
SARMA (1,0) |
660,45 |
|
SARMA (0,1) |
658,36 |
|
SARMA (1,1) |
649,55 |
Sumber: data diolah, 2019
Model terbaik dengan kriteria AIC yang dipilih adalah model SARMA(1,1) karena memiliki nilai AIC terkecil.
Pengujian signifikansi parameter model regresi SARMA (1,1) dilakukan dengan uji Wald. Hasil yang diperoleh adalah sebagai berikut:
Tabel 8. Uji Wald Model Regresi SARMA(1,1)
|
Parameter |
Wald |
P- value ∖ |
|
βl |
-0,56557 |
0,57169 |
|
β2 |
4,39936 |
0,00001 |
|
β3 |
3,18990 |
0,00142 |
|
β4 |
0,51871 |
0,60398 |
|
β5 |
-1,87749 |
0,06045 |
|
Φ |
3,70011 |
0,00022 |
|
θ |
-2,96207 |
0,00717 |
Sumber: data diolah, 2019
Tabel 8 menunukkan bahwa variabel ^2 dan ^3 berpengaruh secara signifikan terhadap variabel Y. Begitu juga dengan variabel Y serta sisaan dari suatu daerah akan berpengaruh secara signifikan terhadap daerah yang dikelilinginya.
Estimasi dari model regresi SARMA (1,1) dapat dituliskan sebagai berikut: n
J=I
n
J=I
Model SARMA (1,1) yang dimiliki oleh setiap kabupaten/kota di Provinsi Jawa Timur berbeda. Hal ini bergantung pada nilai pembobot spasial dari kabupaten/kota yang saling berhubungan. Salah satunya adalah model SARMA (1.1) dari Kabupaten Pacitan yaitu:
XPacitan = -144,89 + 0,08332(0,5Yponorogo +0,5YrTrenggalek) + 0,09932¾ ,Pacitan + 0,02247^3 ,Pacitan - 0,63415(0,5^Ponorogo +0,5 ^Trenggalek )
Interpretasi Model Regresi SARMA
Model SARMA (1,1) pada Persamaan 15 dapat diinterpretasikan sebagai berikut:
-
1. Koefisisien ̂ = 0,08332 bermakna jika
suatu daerah dikelilingi n daerah lain, maka pengaruh dari masing-masing daerah yang mengelilinginya dapat diukur sebesar 0,08332 dikali jumlah kasus pneumonia balita pada daerah di sekitarnya.
-
2. Koefisien ̂ = -0,63415 bermakna jika suatu daerah dikelilingi n daerah lain, maka sisaan dari daerah tersebut dikoreksi oleh sisaan dari daerah tetangganya sebesar -0,63415 dikali nilai pembobot spasial pada daerah disekitarnya.
-
3. Koefisien ̂Q = -144,89 bermakna jika ada variabel X yang bernilai 0, maka jumlah kasus pneumonia balita di setiap kabupaten/kota akan menurun sebesar 144,89. Jika tidak ada faktor yang bernilai 0, maka nilai ̂Q = -144,89 tidak bermakna.
-
4. Koefisien ̂2 = 0,09932 bermakna jika jumlah balita yang mendapat imunisasi dasar lengkap di suatu kabupaten/kota meningkat satu satuan maka akan meningkatkan jumlah kasus pneumonia balita di kabupaten/kota tersebut sebesar 0,09932 apabila faktor-faktor lainnya dianggap konstan. Peningkatan jumlah kasus pneumonia yang harusnya menurun dengan bertambahnya jumlah balita yang mendapat imunisasi dasar lengkap diindikasi disebabkan oleh imunisasi yang dilakukan tidak sesuai untuk penyakit pneumonia. Menurut dr. Nastiti Kaswandani, Sp.A (K) dalam yang dapat mencegah pneumonia adalah vaksin Pneumokokus dan HiB yang belum termasuk dalam program imunisasi dasar lengkap yang dilakukan oleh pemerintah. Vaksin Pneumokokus dan HiB akan menurunkan 50% angka kematian balita akibat pneumonia.
-
5. Koefisien ̂3 = 0,02247 bermakna jika jumlah balita yang mendapatkan
pelayanan kesehatan di suatu
kabupaten/kota meningkat satu satuan maka akan meningkatkan jumlah kasus pneumonia balita di kabupaten/kota tersebut tersebut sebesar 0,02247 apabila faktor-faktor lainnya dianggap konstan. Hal ini sesuai karena semakin banyak balita yang mendapat pelayanan kesehatan berarti semakin banyak balita yang dirawat karena sakit dan ada kemungkinan bahwa penyakit adalah pneumonia.
-
6. Model SARMA (1,1) memiliki nilai R2 sebesar 73,17%. Hal ini berarti faktor-faktor yang berpengaruh dalam penelitian ini mampu menjelaskan jumlah kasus pneumonia balita di Provinsi Jawa Timur sebesar 73,17%, sedangkan sisanya dijelskan oleh faktor lain diluar model.
-
4. KESIMPULAN DAN SARAN
Kesimpulan
-
1. Pada pemodelan jumlah kasus pneumonia di setiap kabupaten/kota di Provinsi Jawa Timur diperoleh bahwa ada
kebergantungan spasial pada variabel dependen dan sisaan dari model pada tingkat pertama, sehingga estimasi model regresi linier dengan koefisien determinasi (R2) sebesar 59,07% kurang baik untuk memodelkan jumlah kasus pneumonia tersebut. Oleh karena itu model yang dipilih adalah regresi SARMA (1,1) dengan AIC sebesar 649,55 dan R2 sebesar 73,17%.
-
2. Faktor yang berpengaruh secara signifikan terhadap jumlah kasus pneumonia balita pada setiap kabupaten/kota di Provinsi Jawa Timur adalah jumlah balita yang mendapat imunisasi dasar lengkap dan jumlah balita yang mendapat pelayanan kesehatan
Saran
-
1. Niai R2 yang diperoleh dari model belum cukup tinggi. Disarankan untuk menambahkan variabel independen yang diduga signifikan serta mempertimbangkan kelinieran dari model.
-
2. Dalam penelitian selanjutnya disarankan untuk menggunakan data balita yang
mendapat vaksin pneumokokus dan HiB agar faktor yang berpengaruh terhadap jumlah kasus pneumonia lebih akurat lagi.
DAFTAR PUSTAKA
Anselin, L., 1988. Spatial Econometrics:
Methods and Models. Netherlands: Kluwer Academic Publishers.
Dinas Kesehatan Provinsi Jawa Timur. 2018. Profil Kesehatan Provinsi Jawa Timur Tahun 2017. Jawa Timur: Dinkes Provinsi Jawa Timur.
Gujarati, D. N. & Porter, D. C., 2009. Basic Econometrics. Fifth Edition ed. New York: McGraw-Hill/Irwin,.
Huang, J. S., 1984. The Autoregressive Moving Average Model for Spatial Analysis. Austral. J. Statist, Volume 26(2), pp. 169178.
Ikatan Dokter Anak Indonesia. 2017. Sekilas Vaksin Pneumokokus. http://www.idai. or.id/artikel/klinik/imunisasi/sekilas-vaksin-pneumokokus. Diakses: 6 Mei 2019.
Kruk, R. v. d., 2002. A General Spatial ARMA Model: Theory and Application (online). https://core.ac.uk/download/pdf/7036080.p df. Diakses: 8 November 2018
Kutner, M. H., Nachtsheim, C. J., Neter, J. & LI, W., 2005. Applied Linear Statistical Model. Fifth Edition ed. New York: McGraw-Hill/Irwin.
Qauliyah, Asta. 2010. Referat Kedokteran: Etiologi dan Patofisiologi Penyakit Pneumonia.https://www.astaqauliyah.com/ blog/read/1924/referat-kedokteran-etiologi-dan-patofisiologi-penyakit-pneumonia.html. Diakses 7 Januari 2019.
DOI: https://doi.org/10.24843/MTK.2019.v08.i03.p259
Lampiran 1. Peta Wilayah Provinsi Jawa Timur
Peta Provinsi Jawa Timur
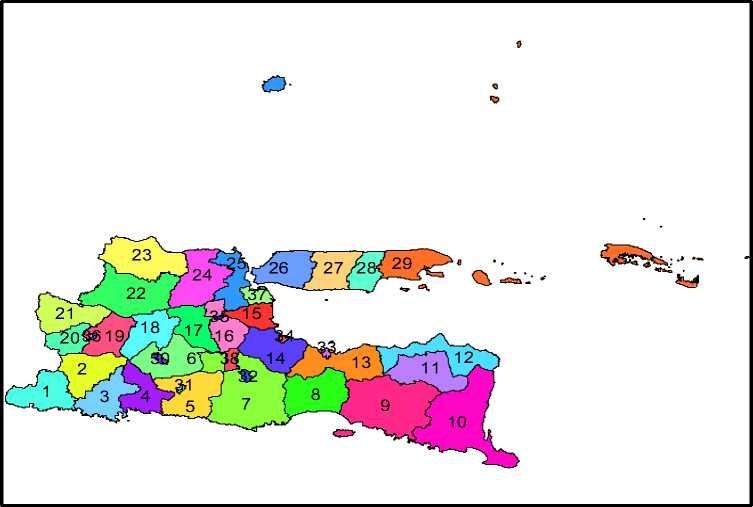
Provinsi Jawa Timur
^∣ 1. Pacitan
~| 2. Ponorogo
~| 3. Trenggalek
I I 4. Tulungagung ~l 5. Blitar ^^ 6. Kediri
awa_1t.imPaucr.itsahnp>1 a Ia n g
-
2. . Ponorogoi majang
-
3. Trenggalek
-
4. Tulungagung jer
-
5. Blitar
-
6. KediriI Banyuwangi
-
78. . LMuamlaanjgangJond owoso
-
91. 0.JeBmanbyeurwangij bon do
-
1112. . SBiotnubdoonwdooso^bolinggo
-
13. Probolinggosu ru a n
-
14. Pasuruan
-
16. . Mojokertoidoarjo
-
17. JombangIojokerto
-
18. Nganjuk
-
19. MadiunJombang
-
2201. . NMgaagwetian Iganjuk
-
2223. . TBuobjoannegoro idiun
-
2245. . LGarmesoikngan g eta n
-
2267. . SBaamngpkaanlagn jawi
-
2289. .. PSaummaeknaespan•jonegoro
-
3301. . KKoottaa__kbelidtairriban
-
32. Kota_malangnongan
-
33. Kota_probolinggo
-
34. Kota_pasuruani k
-
35. Kota_mojokerto
-
36. Kota_madiunigkalan
-
38. . Kootaa__sbuartau aya
~| 28. Pamakasan
I 29. SumenN
I 30. Kota_kediri
2 31. Kota_blitar ■ 32.Wota_malang E
I 33. Kota_probolinggo
~| 34. Kota_pasuruan
I I 35. Kota_rrS>jokerto
I__f 36. Kota_madiun
I__3 37. Kota_su rabaya
I j 33. Kota_batu
Lampiran 2. Peta Tematik Variabel Penelitian
Peta Penyebaran Jumlah Balita yang Mendapat
ASI Eksklusif di Provinsi Jawa Timur
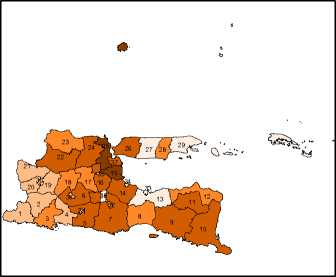
1.shp
108 - 669
670 - 1466
1467 - 2378
□ 2379 - 4736
M 4737 - 8747

1.shp
136 - 2099
2100 - 3808
3809 - 9202 M 9203 - 16424 □ 16425 - 26976

Peta Penyebaran Jumlah Balita yang Mendapat
Imunisasi Dasar Lengkap di Provinsi Jawa Timur
1.shp
1592 - 5681
5682 - 12159
12160 - 18374
M 18375 - 23826 □ 23827 - 40078

(a)
(b)
(c)
Peta Penyebaran Jumlah Balita yang Mendapat Pelayanan Kesehatan di Provinsi Jawa Timur
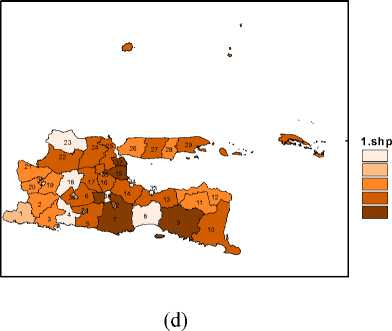
517 - 11702
11703 - 25178
25179 - 43963
43964 - 80529
80530 - 149176
Peta Penyebaran Jumlah Rumah Tangga ber-PHBS di Provinsi Jawa Timur
N
W

E
S
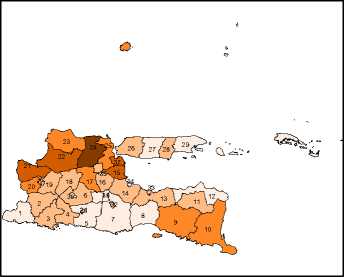
1.shp
1996 - 15042
15043 - 38551
38552 - 96523 □ 96524 - 166094 □ 166095 - 362999
(e)

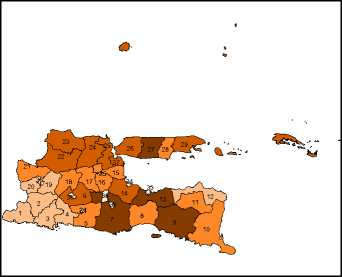
1.shp
7280 - 35890
35891 - 99030 99031 - 138540
CZ 138541 - 211920 □ 211921 - 283960

(f)
245
Discussion and feedback