MODEL GEOGRAPHICALLY WEIGHTED REGRESSION (GWR) FAKTOR-FAKTOR YANG MEMENGARUHI KECELAKAAN LALU LINTAS DI PROVINSI BALI

E-Jurnal Matematika Vol. 8(2), Mei 2019, pp.140-147

DOI: https://doi.org/10.24843/MTK.2019.v08.i02.p245

ISSN: 2303-1751

MODEL GEOGRAPHICALLY WEIGHTED REGRESSION (GWR) FAKTOR-FAKTOR YANG MEMENGARUHI KECELAKAAN LALU LINTAS DI PROVINSI BALI

Ni Kadek Endah Yanita Utari^1§, I Gusti Ayu Made Srinadi², Made Susilawati³

• ¹Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: endah.yanit4@gmail.com]

• ²Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]

• ³Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id] ^§Corresponding Author

ABSTRACT

The number of traffic accidents in Bali kept increasing since 2015 until 2017. The factors that affected the traffic accidents in every region were suspected to be varied according to geographic position. This geographic effect was known as spatial heterogeneity. Spatial heterogeneity was analized by using Geographically Weighted Regression (GWR). This study aim to model the factors which affected the traffic accidents in every subdistrict in Bali by using fixed and adaptive gaussian kernel. The result showed that GWR with adaptive gaussian kernel was better at estimated the models because it had higher value of R² which was at 90,64%. The factors which significantly affected the number of traffic accident in 57 subdistrict in Bali were the average rainfall and the number of population within age of 15 to 29 years old.

Keywords: traffic accidents, spatial heterogeneity , geographically weighted regression (GWR), adaptive kernel gaussian

2015 terjadi 1.492 kejadian, tahun 2016 terjadi 1.580 dan pada tahun 2017 terjadi 1.698 kejadian. Faktor utama yang dapat memengaruhi terjadinya kecelakaan lalu lintas adalah faktor manusia, kendaraan, jalan, selain itu faktor lingkungan dan cuaca juga dapat berpengaruh terhadap terjadinya kecelakaan lalu lintas (Putri, 2014).

Provinsi Bali terdiri dari 9 kabupaten/kota dengan 57 kecamatan. Secara geografis masing-masing kecamatan memiliki karakteristik yang berbeda-beda, misalnya dari segi jumlah penduduk, luas wilayah maupun kepadatan penduduk. Melihat kasus kecelakaan di Bali terus mengalami peningkatan dan perbedaan karakteristik yang dimiliki oleh masing-masing kecamatan, maka dalam penelitian ini diharapkan diketahui hubungan kecelakaan lalu lintas dan faktor-faktor yang memengaruhinya di setiap kecamatan yang ada di Provinsi Bali.

Pada umumnya untuk mengetahui model hubungan antara variabel bebas dengan variabel terikat digunakan metode regresi linier (Dewi & Zain 2016). Namun, metode regresi linier tidak memperhatikan letak geografis, setiap wilayah diasumsikan memiliki karakteristik yang sama. Oleh karena itu, digunakan suatu metode yang memperhatikan letak geografis yaitu metode geographically weighted regression (GWR). GWR menghasilkan penaksir parameter model yang bersifat lokal untuk setiap titik atau lokasi dimana data tersebut diamati (Caraka & Yasin, 2017).

Secara umum, model GWR dapat dinyatakan sebagai berikut (Caraka & Yasin, 2017):

ΣP

β_k (u ,,v )x _ik + ε _i

k=ι

dengan i = 1,2, .,n dan n merupakan

banyaknya pengamatan,    y_i menyatakan

variabel terikat pada pengamatan ke- i, Xi_k

menyatakan variabel bebas ke-k pada pengamatan ke- i, β₀(u ,,v) merupakan konstanta regresi pada lokasi pengamatan ke- i, (ui, v i) merupakan koordinat letak geografis (longitude,latitude) dari lokasi pengamatan kei, β_k(u,, v) menyatakan koefisien regresi ke- k pada lokasi pengamatan ke- i dan ε_i merupakan error pengamatan ke- i.

Penelitian mengenai kecelakaan lalu lintas menggunakan metode GWR pernah dilakukan oleh Dewi & Zain (2016) di Jawa Timur. Variabel bebas yang digunakan adalah kepadatan penduduk, persentase usia remaja, persentase kecelakaan terjadi di kawasan jalan kabupaten/kota, persentase pendidikan terakhir pelaku adalah di atas SMP, rasio jenis kelamin dan persentase kecelakaan terjadi pada waktu gelap. Fungsi pembobot yang digunakan adalah fixed Gaussian, adaptive Gaussian, fixed bisquare, adaptive bisquare, fixed tricube dan adaptive tricube. Hasil dari penelitian tersebut, diperoleh bahwa tidak ada perbedaan antara model regresi linier berganda dengan model GWR. Penelitian tersebut menyatakan bahwa, model GWR dengan pembobot fixed bisquare lebih baik karena memiliki nilai R² yang lebih

besar dibandingkan dengan pembobot lain yang digunakan. Faktor-faktor yang berpengaruh signifikan adalah kepadatan penduduk dan persentase pendidikan terakhir pelaku kecelakaan adalah di atas SMP.

Penelitian Agustianto et al., (2018) yang memodelkan faktor penyebab kecelakaan lalu lintas di Kalimantan Barat menggunakan metode GWR. Fungsi pembobot yang digunakan adalah fixed kernel yaitu Gaussian, bisquare, dan tricube. Variabel bebas yang digunakan adalah jumlah penduduk, panjang kondisi jalan rusak, rasio jenis kelamin, dan jumlah pelanggaran lalu lintas. Selain itu, hasil uji kesesuaian model menyatakan bahwa tidak ada perbedaan antara model regresi linier berganda dengan model GWR namun model GWR dengan fungsi pembobot fixed kernel gaussian lebih sesuai digunakan. Faktor yang berpengaruh signifikan adalah jumlah pelanggaran lalu lintas.

Berdasarkan paparan di atas, penulis melakukan penelitian mengenai faktor-faktor yang memengaruhi kecelakaan lalu lintas pada masing-masing kecamatan yang ada di Provinsi Bali menggunakan metode GWR.

• 2. METODE PENELITIAN

• 2.1    Sumber Data

Penelitian ini menggunakan data sekunder tahun 2017 yang diperoleh dari tiga sumber yaitu Polda Bali, Badan Pusat Statistik (BPS), dan Badan Meteorologi, Klimatologi dan Geofisika (BMKG). Unit amatan yang digunakan pada penelitian adalah 57 kecamatan yang ada di Provinsi Bali.

• 2.2    Variabel Penelitian

Variabel yang digunakan dalam penelitian ini terdiri dari satu variabel terikat (F) dan tiga variabel bebas (X).

Tabel 1. Variabel Penelitian

No              Variabel              Skala

• ¹    Jumlah kecelakaan lalu lintas ( F)    Rasio

• ²   Kepadatan penduduk (X₁)          Rasio

• 3    Rata-rata curah hujan (X₂ )           Rasio

• ⁴   Penduduk usia 15-29 tahun (X₃ )     Rasio

• 2.3 Analisis Data

Langkah-langkah analisis data yang digunakan dalam penelitian ini sebagai berikut:

• 1.    Mendeskripsikan data dengan melakukan analisis statistika deskriptif.

• 2.    Membentuk model regresi linier berganda, dengan tahapan-tahapan sebagai berikut:

• a.    Menduga parameter model regresi linier berganda menggunakan metode Ordinary Least Square (OLS).

β — (X^τX)^{- 1}X ^τY.           (1)

• b.    Memeriksa kenormalan    sisaan

menggunakan uji Anderson Darling (Gujarati, 2004).

Hipotesis uji:

H₀: Residual berdistribusi normal

H₁: Residual tidak berdistribusi normal Statistik uji:

A² = —n — -∑"- ι(2 i - 1) { ln^ffi) + ln[1 — F‰ ₁₊₁)]}                (2)

dengan, F(Vj) adalah fungsi distribusi kumulatif dari normal baku dan adalah data yang diurutkan.

Kriteria pengujian:

Jika A² > AD_tabei maka H₀ ditolak.

• c.    Melakukan uji serentak (Uji F).

Hipotesis uji:

• ^ho ^: βo — ^β1 ^— " ^— βk — O^

• H₁: minimal ada satu β_k ≠ O, k — 1,2,3,...,p.

Statistik uji:

_{f    =}     [∑Hι(yt -y)² ]/(p)

• ^h11    [∑" βy_l -yt )² W -p - i)      .

(3)

Kriteria pengujian:

Jika Fft i t > F_a(-p,_n-p - i) atau Pa_a iue < , maka ditolak.

• d.    Melakukan uji parsial (Uji t).

Hipotesis uji:

H : βk — O, H₀ tβ_k≠O, k— 1,2,3.....p.

Statistik uji:

P.

^{th it —} Ξ≡c⅛) .              ⁽⁴⁾

Kriteria pengujian:

Jika ∣tf_l f 11 > t^,_{n- p - 1} / atau ^Paa Iue < , maka ditolak.

• 3.    Melakukan uji multikolinieritas dengan melihat nilai variance inflation factor (VIF) (Montgomery et al., 2012).

Hipotesis uji:

H₀: Tidak ada multikolinearitas antarvariabel bebas dalam model regresi, H₁: Ada multikolinearitas antarvariabel bebas dalam model regresi.

Statistik uji:

VIFi — A          (5)

dengan j — 1,2,3,", k, dengan k menyatakan banyaknya variabel bebas, dan R² menyatakan koefisien determinasi variabel bebas ke-j.

Kriteria pengujian:

Jika nilai VIF > 5 maka H₀ ditolak.

• 3.    Menyelidiki adanya heterogenitas spasial menggunakan uji Breusch Pagan (Anselin, 1988).

Hipotesis uji:

^H0: ^σ1 ^{— σ}2 ^— '" ^{— σ}n ^{— σ ,} H₁: Minimal terdapat satu σj² ≠ σ². Statistik uji:

BP — 1f^τ X(X^τX)^{- 1} X^t f     (6)

dengan, BP merupakan nilai uji Breusch Pagan, X merupakan matriks berukuran n × (k + 1), dan f merupakan vektor berukuran (n × 1) yang elemennya didefinisikan sebagai:

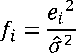
dengan,

y? p-²

Q² ₌ ∑i=i^e_-

e j² — (Y_i-Y_i)²

dengan, Q² merupakan varian galat dan e² merupakan nilai kuadrat galat.

Kriteria pengujian:

Jika nilai B P > χ_k² atau p_{α a} ι_ue < a maka H₀ ditolak.

• 4.    Membentuk model GWR dengan tahapan-tahapan sebagai berikut:

• a.    Mengonversi koordinat longitude dan latitude menjadi satuan kilometer (km) masing-masing kecamatan.

• b.    Menghitung jarak Euclid antarkecamatan.

d i j ^— J(i¾-i¾y + ⅛-⅛².  (7)

• c.    Menghitung nilai bandwidth optimum menggunakan metode cross validation (CV) (Fotheringham et al., 2002).

CV =∑ill^[Vi - ̂ ≠i (b)] ²    (8)

• d.    Menghitung matriks pembobot dengan fungsi pembobot fixed kernel gaussian dan adaptive kernel gaussian.

• 1.    Fixed Kernel Gaussian

^wH =exp[-i^. ⅛^/ ],    (9)

• 2.    Adaptive Kernel Gaussian

^wC =exp[-i^. ⅜^/ ].   (10)

Hal yang membedakan dari

persamaan (9) dan (10) adalah pada

nilai bandwidth. Fungsi fixed kernel gaussian memiliki bandwidth yang sama untuk setiap titik lokasi pengamatan, sedangkan fungsi

adaptive kernel gaussian memiliki

bandwidth yang berbeda untuk masing-

e.

f.

masing titik lokasi pengamatan.

Menduga parameter model GWR berdasarkan matriks pembobot yang telah diperoleh.

Pengujian kesesuaian model GWR

menggunakan uji F (Caraka & Yasin, 2017).

Hipotesis uji:

Hq :     (^i ^, Vi)=βk , dengan =

1,2,3,…,P dan i=1,2,3,…,n

H^ : Minimal ada satu βk (U_i, V_i)≠βk , dimana k=1,2,3,…,P dan = 1,2,3,…,n

Statistik uji:

Matriks S merupakan proyeksi dari model GWR yang memproyeksikan nilai y menjadi ̂ pada lokasi (U_i , V_i). Kriteria pengujian:

Jika ∏hit ^> Ftabel (a; df₁ , df₂ ) maka ∏o ditolak.

g. Pengujian signifikansi model GWR menggunakan uji t (Caraka & Yasin,

2017).

Hipotesis uji:

H₀ :  (U_i, V_i)=0,k=1,2,3,…P

H^ : Minimal ada satu βk (U_i, V_i)≠0, k=1,2,3,…P

Statistik uji:

̂

=     ⁽ U₁ ^, U₁ ⁾(12)

hitung   _SE ^̂(12)

₍ ^uI, ^vI )

dengan,

_̂_

SE βk(u_i,u_i) =√var βk(u_i,u_i )

= √CC^τσ²

5.

C=(X^tW(U_i, v_i )X)~¹X^τW(U_i, v_i )

₂    ^∑   ( Yi - ̂ _i )²

=

Kriteria pengujian:

Jika | ^-hitung |> ^tabel .f; n-p-1/^, maka Hq ditolak.

Interpretasi hasil.

• 3.    HASIL DAN PEMBAHASAN

  • 3.1    Statistika Deskriptif

Statistika deskriptif mengenai jumlah kecelakaan lalu lintas di Provinsi Bali dan faktor-faktor yang memengaruhinya disajikan pada Tabel 2.

Tabel 2 Statistika Deskriptif

,   —^SSE (H₀)/dfi

hit =    (H₁)/df₂

dengan,

SSE ( Ho )   : Y^t (I-H)Y , dengan

H= (X^tX)-¹X^t

SSE ( Hi )   : Y^t (I-S)T(I-S)Y

dfi       :n-P-1

df₂       : (n-2tr (S)+tr (S^tS))

Variabel	Min	Maks	Mean	St. Dev
Y	6	147	33,91	31,784
X1	162	6.009	1.253,39	1.382,407
X	93,250	393,125	223,317	70,314
X 3	2.960	92.540	17.223,33	17.000,176

^X1^T (X^tW(u_i, ^vi )X)~¹X^rW(u_i, u_i )

⎢ X₂' (X^rW(U_i , u_i )X)-¹X^rW(U_i , u_i)⎥ ⎢⋮⎥

⎣   (X^rW(u_i , u_i )X)-¹X^rW(U_i, u_i)⎦

Tabel 2 menunjukkan bahwa di Provinsi Bali pada tahun 2017, jumlah kecelakaan lalu lintas (Y) yang tertinggi sebesar 147 satuan sedangkan yang terendah sebesar 6 satuan. Kondisi tertinggi terletak di Kecamatan Denpasar Barat sedangkan kondisi terendah terletak di Kecamatan Pupuan, Nusa Penida, dan Selat (Polda Bali, 2018 Komunikasi Personal)

Kepadatan penduduk (^l ) tertinggi sebesar 6009 satuan sedangkan terendah sebesar 162 satuan. Kondisi tertinggi terletak di Kecamatan Kuta sedangkan kondisi terendah terletak di Kecamatan Selemadeg Barat (BPS, 2018).

Rata-rata curah hujan (%2 ) tertinggi sebesar 393,125 satuan sedangkan yang terendah sebesar 93,250 satuan. Kondisi tertinggi terletak di Kecamatan Bebandem sedangkan kondisi terendah terletak di Kecamatan Seririt (BMKG, 2018 Komunikasi Personal).

Selanjutnya, penduduk usia 15-29 tahun ( ■^3) tertinggi sebesar 92540 satuan sedangkan yang terendah sebesar 2960 satuan. Kondisi tertinggi terletak di Kecamatan Denpasar Selatan sedangkan kondisi terendah terletak di Kecamatan Selemadeg dan Selemadeg Barat (BPS, 2018).

• 3.2    Pemodelan Regresi Linier Berganda

Model regresi linier berganda yang terbentuk untuk jumlah kecelakaan lalu lintas di Provinsi Bali tahun 2017 adalah sebagai berikut:

^̂i = 23,93881 + 0,00742 *1 - 0,08067 X₂ + 0,001085 X₃

• a.    Uji Kenormalan

Uji kenormalan dilakukan untuk mengetahui residual berdistribusi normal atau tidak. Berdasarkan uji Anderson Darling diperoleh p-value sebesar 0,1178 pada taraf signifikansi a = 0,05. Karena p-value > a, maka gagal untuk menolak Hq . Hal tersebut berarti residual berdistribusi normal.

• b.    Uji Serentak (uji F)

Uji F dilakukan untuk mengetahui pengaruh semua variabel bebas (X) terhadap variabel terikat (Y). Berdasarkan hasil analisis Uji F diperoleh p-value sebesar 2,2×10 16 pada taraf signifikansi a = 0,05, karena p-value < a maka Hq ditolak. Hal tersebut berarti minimal ada satu variabel bebas ke-k yang berpengaruh signifikan terhadap variabel terikat.

• c.    Uji Parsial (uji t)

Uji parsial dilakukan untuk mengetahui variabel bebas mana saja yang berpengaruh signifikan terhadap variabel terikat. Hasil analisis dengan uji t disajikan pada Tabel 3.

Tabel 3 Hasil Uji Parsial

Variabel	P-value	Kesimpulan
Kepadatan Penduduk ( *1 )	0,001	Tolak H0
Rata-rata Curah Hujan (x?. )	0,001	Tolak H0
Usia Penduduk 15 29 Tahun (X-I )	0,000	Tolak H0

Berdasarkan Tabel 3 dapat disimpulkan bahwa semua variabel bebas berpengaruh signifikan terhadap variabel terikat. Hal tersebut dapat dilihat pada kesimpulan yang menolak H₀ .

• 3.3    Uji Multikolinieritas

Uji multikolinieritas dilakukan untuk menyelidiki ada tidaknya korelasi antara dua atau lebih variabel bebas. Berdasarkan hasil analisis, nilai VIF masing-masing variabel bebas disajikan dalam Tabel 4.

Tabel 4 Hasil Uji Multikolinieritas

Variabel bebas                  2__________³

VIF    3,996621   1,052691    4,085825

Tabel 4 menunjukkan bahwa masing-masing variabel bebas memiliki nilai VIF<5, dengan demikian dapat disimpulkan bahwa tidak ada multikolinieritas antarvariabel bebas.

• 3.4    Uji Heterogenitas Spasial

Tujuan dilakukan uji heterogenitas spasial adalah untuk menyelidiki adanya perbedaan karakteristik antarwilayah dalam model regresi linier berganda.

Perhitungan menggunakan uji Breusch Pagan menghasilkan p-value sebesar 7,276 × 10 ⁵ pada taraf signifikansi = 0,05, karena p-value < a maka Hq ditolak. Hal tersebut berarti terdapat heterogenitas spasial pada data.

Adanya heterogenitas spasial menyebabkan metode regresi linier berganda kurang tepat digunakan untuk mengetahui faktor-faktor yang memengaruhi kecelakaan lalu lintas pada masing-masing kecamatan yang ada di Provinsi Bali. Hal tersebut dikarenakan metode regresi linier tidak memperhatikan perbedaan karakteristik antarwilayah artinya metode tersebut menghasilkan penduga parameter yang bersifat global. Oleh karena itu, dilakukan pemodelan lebih lanjut menggunakan metode yang dapat mengatasi adanya heterogenitas spasial yaitu metode geographically weighted regression (GWR) (Fotheringham et al., 2002).

• 3.5    Pemodelan Geographically Weighted

Regression (GWR)

Langkah awal dalam membentuk model GWR adalah dengan mengonversi koordinat lintang dan bujur yang diperoleh dari Google Map masing-masing kecamatan yang ada di Provinsi Bali dari satuan degree minute second (DMS) menjadi satuan kilometer (km). Selanjutnya menentukan matriks pembobot yang dalam penelitian ini dihitung menggunakan dua fungsi, yaitu fixed kernel gaussian dan adaptive kernel gaussian. Perhitungan matriks pembobot memerlukan jarak Euclid dan nilai bandwidth optimum. Nilai bandwidth optimum diperoleh dengan metode CV.

Setelah diperoleh matriks pembobot menggunakan fixed kernel gaussian dan adaptive kernel gaussian maka akan diperoleh model untuk setiap kecamatan yang ada di Provinsi Bali.

• 3.6    Pengujian Kesesuaian Model GWR

Berdasarkan hasil perhitungan uji F, diperoleh nilai ^hitung model GWR dengan pembobot fixed kernel gaussian sebesar 2,314889 dengan Ftabel (a; Afr , Af₂ ) sebesar 1,668353 yang berarti Fhitung > Ftabel sehingga Hq ditolak, dengan demikian dapat disimpulkan bahwa ada perbedaan yang signifikan antara model regresi dengan model GWR dengan pembobot fixed kernel gaussian.

Selanjutnya, nilai Fhitung model GWR dengan pembobot adaptive kernel gaussian sebesar 3,051497 dengan Ftabel (a; Afi , Af₂ ) sebesar 1,644949 yang berarti Fhitung > Ftabel sehingga Hq ditolak, dengan demikian dapat disimpulkan bahwa ada perbedaan yang signifikan antara model regresi dengan model GWR dengan pembobot adaptive kernel gaussian.

• 3.7    Uji Signifikansi Parameter Model GWR

Uji signifikansi parameter dilakukan dengan menguji parameter secara parsial (uji t) untuk mengetahui pengaruh signifikansi masing-masing variabel bebas terhadap variabel terikat.

Tabel 5. Contoh hasil uji t Kecamatan Selemadeg dengan Fixed Kernel Gaussian

Variabel	Nilai ̂	| ^hitung |	^tabel
*1	0,00351	1,23214	2,30687
X2	-0,09881	2,74384	2,30687
X2	0,00142	5,96231	2,30687
Tabel 6.	Contoh hasil uji t Kecamatan Selemadeg dengan Adaptive Kernel
	Gaussian
Variabel	Nilai ̂	| ^hitung |	^tabel
Xt	0,00349	1,270895	2,30687
χ2	-0,09872	2,83664	2,30687
X2	0,00142	6,176635	2,30687

Berdasarkan Tabel 5 dan 6, dapat dilihat bahwa variabel bebas yang berpengaruh signifikan terhadap variabel terikat adalah rata-rata curah hujan (¾) dan usia penduduk 15-29 tahun ( X3), karena nilai | t hitung|> ^tabel sehingga H o ditolak.

Adapun variabel yang berpengaruh signifikan pada masing-masing kecamatan di Provinsi Bali dengan pembobot fixed kernel gaussian diperoleh 5 kelompok yang disajikan pada Tabel 7.

Selanjutnya, variabel yang berpengaruh signifikan pada masing-masing kecamatan di Provinsi Bali dengan pembobot adaptive kernel gaussian diperoleh 4 kelompok yang disajikan pada Tabel 8.

Tabel 7 Hasil uji t setiap kecamatan

Kecamatan	Variabel yang signifikan
Kintamani, Tejakula, Kubu dan Abang.	*1
Selemadeg Barat, Pupuan, Gerokgak, Seririt, Busungbiu, Banjar, Sukasada, Buleleng, Sawan, Kubutambahan, Melaya, Negara, Jembrana, Mendoyo dan Pekutatan.	X3
Nusa Penida, Klungkung, Dawan, Rendang, Sidemen, Manggis, Karangasem, Bebandem, Selat, Tampaksiring, Tegallalang, Susut, Bangli dan Tembuku.	^^ dan Jf 3
Selemadeg, Selemadeg Timur, Kerambitan, Tabanan, Kediri, Marga, Penebel, Sukawati, Blahbatuh, Ubud, Kuta Selatan, Kuta, Kuta Utara, Mengwi, Abiansemal, Denpasar Selatan, Denpasar Timur, Denpasar Barat dan Denpasar Utara.	Jf 2 dan Jf 3
Baturiti, Banjarangkan, Gianyar, Payangan dan Petang.	*1 , X2 , dan X3 ∖

Tabel 8 Hasil uji t setiap kecamatan

Kecamatan	Variabel yang signifikan
Pupuan, Banjarangkan, Gianyar, Gerokgak, Seririt, Busungbiu, Banjar dan Sukasada.	χ3
Klungkung, Dawan, Rendang, Sidemen, Manggis, Karangasem, Abang, Bebandem, Selat, Kubu, Tampaksiring, Tegallalang, Payangan, Sawan, Kubutambahan, Tejakula, Petang, Susut, Bangli, Tembuku dan Kintamani.	^l dan Jf 3
Selemadeg, Selemadeg Timur, Selemadeg Barat, Kerambitan, Tabanan, Kediri, Marga, Penebel, Sukawati, Blahbatuh, Ubud, Kuta Selatan, Kuta, Kuta Utara, Mengwi, Abiansemal, Denpasar Selatan, Denpasar Timur, Denpasar Barat, Denpasar Utara, Negara, Jembrana, Mendoyo dan Pekutatan.	Jf 2 dan Jf 3
Baturiti, Nusa Penida, Buleleng dan Melaya.	■^1 , Jf 2 , dan Jf 3

• 3.8    Pemilihan Model Terbaik

Untuk mengetahui model GWR terbaik yang dapat digunakan untuk memodelkan jumlah kecelakaan lalu lintas di Provinsi Bali adalah dengan membandingkan rata-rata nilai R² fixed kernel gaussian dan adaptive kernel gaussian.

Tabel 9. Perbandingan Model GWR

Model              R²

GWR Fixed Kernel Gaussian     0,9033

GWR Adptive Kernel Gaussian   0,9064

Tabel 9 menyatakan bahwa secara matematika nilai rata-rata R² terbesar secara keseluruhan dimiliki oleh model GWR dengan pembobot adaptive kernel gaussian. Selanjutnya, dilakukan uji t independen, untuk mengetahui model terbaik secara statistika. Hipotesis yang digunakan adalah sebagai berikut:

H₀ :    fixed = R² adaptif (Tidak ada

perbedaan antara nilai R² fixed dan R² adaptif) H^ :   fixed ≠ R² adaptif (Ada perbedaan

antara nilai R² fixed dan R² adaptif)

Jika P- value <a = 0,05, maka H₀ ditolak.

Berdasarkan hasil analisis diperoleh P- value sebesar 0,422 yang berarti P-value >a (0,05), sehingga gagal untuk menolak Hq . Oleh karena itu, secara statistik tidak ada perbedaan antara nilai R² fixed dan R² adaptif.

Dengan demikian, dapat disimpulkan bahwa secara statistika, nilai R² antara fixed dengan adaptif tidak ada perbedaaan tetapi secara matematika nilai R² adaptif lebih baik. Sehingga model terbaik yang dapat digunakan untuk memodelkan jumlah kecelakaan lalu lintas pada masing-masing kecamatan yang ada di Provinsi Bali adalah model GWR dengan pembobot adaptif kernel gaussian.

• 3.9    Interpretasi Hasil

Setelah diperoleh model GWR terbaik untuk memodelkan jumlah kecelakaan lalu lintas pada masing-masing kecamatan yang ada di Provinsi Bali, selanjutnya dilakukan

interpretasi model GWR. Sebagai contoh, model GWR dengan pembobot adaptive kernel gaussian Kecamatan Selemadeg adalah sebagai berikut:

̂ j = 29,48885 - 0,09872 X₂ + 0,00142 X₃

Interpretasi dari model tersebut adalah apabila rata-rata curah hujan (^2 ) pada Kecamatan Selemadeg meningkat sebesar satu satuan, maka dapat menurunkan jumlah kecelakaan lalu lintas sebesar 0,09872 satuan dengan variabel bebas lainnya dianggap konstan. Interpretasi untuk variabel bebas lainnya juga sama, nilai untuk masing-masing parameter menentukan besarnya kenaikan ataupun penurunan.

• 4.    KESIMPULAN DAN SARAN

Berdasarkan hasil dan pembahasan, dapat disimpulkan bahwa terdapat heterogenitas spasial yang berarti terdapat perbedaan karakteristik antarwilayah sehingga dilakukan pemodelan menggunakan metode GWR. Model GWR dengan pembobot adaptive kernel gaussian lebih sesuai digunakan untuk memodelkan jumlah kecelakaan lalu lintas pada masing-masing kecamatan yang ada di Provinsi Bali karena secara keseluruhan variabel bebasnya mampu menjelaskan variabel terikat sebesar 90,64 %.

Variabel bebas pada model GWR dengan pembobot adaptive kernel gaussian yang berpengaruh signifikan dapat dikelompokkan menjadi empat kelompok. Variabel bebas yang paling dominan berpengaruh terhadap jumlah kecelakaan lalu lintas di 57 kecamatan yang ada di Provinsi Bali adalah rata-rata curah hujan (^2) dan penduduk usia 15-29 tahun (X₃).

Diharapkan kepada masyarakat yang mengendarai kendaraan bermotor agar selalu berhati-hati terlebih pada situasi hujan dan kepada orang tua agar tidak membiarkan anaknya yang masih di bawah umur untuk mengendarai kendaraan serta kepada pihak yang berwajib diharapkan agar dilakukan pengetatan dalam pemberian SIM agar

mengurangi jumlah kecelakaan lalu lintas di Provinsi Bali.

DAFTAR PUSTAKA

Agustianto, S.P., Martha, S. & Satyahadewi, N. 2018. Pemodelan Faktor Penyebab Kecelakaan Lalu Lintas di Kalimantan Barat  dengan  Metode Geographically

Weighted Regression (GWR). Buletin Ilmiah  Math.  Stat. dan Terapannya

(Bimaster), 7(4): 303 – 310.

Anselin, L. 1988. Spatial Econometrics: Methods and Models. London: Kluwer Academic Publishers.

BPS 2018. Provinsi Bali Dalam Angka. Denpasar: BPS Provinsi Bali.

Caraka, R.E. & Yasin, H. 2017. Geographically Weighted Regression (GWR) Sebuah Pendekatan Regresi Geografis. First ed. Yogyakarta: Mobius.

Dewi, P.L.A. & Zain, I. 2016. Pemodelan Faktor-Faktor Penyebab Kecelakaan Lalu Lintas Berdasarkan Metode Geographically Weighted Regression di Jawa Timur. Jurnal Sains dan Seni ITS, 5(1): 58-64.

Fotheringham, A.S., Brunsdon, C. & Charlton, M. 2002. Geographically Weighted Regression:  The Analysis of Spatially

Varying Relationships. England: John Wiley & Sons Ltd.

Gujarati, D.N. 2004. Basic Econometrics. Fourth ed. New York: The McGraw-Hill.

Montgomery, D.C., Peck, E.A. & Vining, G.G. 2012. Introduction to Linear Regression Analysis. Fifth ed. New Jersey: John Wiley & Sons, Inc.

Putri, C.E. 2014. Analisis Karakteristik Kecelakaan dan Faktor Penyebab Kecelakaan Pada Lokasi Blackspot di Kota Kayu Agung. Jurnal Teknik Sipil dan Lingkungan, 2(1): 154–161.

Undang-Undang Nomor 56 Tahun 1960 tentang Penetapan Luas Tanah Pertanian.

147