PENERAPAN STATIC HEDGE DALAM PENGELOLAAN RISIKO PADA OPSI TIPE BARRIER
on
E-Jurnal Matematika Vol. 7(4), November 2018, pp. 357-363
DOI: https://doi.org/10.24843/MTK.2018.v07.i04.p225
ISSN: 2303-1751
PENERAPAN STATIC HEDGE DALAM PENGELOLAAN RISIKO PADA OPSI TIPE BARRIER
Ni Made Nita Astuti1§, Komang Dharmawan2, Tjokorda Bagus Oka3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdnithaastuti@yahoo.co.id]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: k.dharmawan@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: bagusoka@unud.ac.id]
§Corresponding Author
ABSTRACT
The barrier option is an option whose payoff depends on whether the underlying asset touches the barrier or not during the lifetime of the option. The determination of the barrier option requires a numerical approach, one of which is the Binomial Tree model. The purpose of this study is to determine barrier option type down and out call on a static hedging using the Binomial Tree model and compare it with the analytic value. The results show that the increases in strike price would decrease the option value. Moreover, values from 80 periods using the Binomial Tree model for the four strike prices are close to analytic with error less than or equal to 0.00182.
Keywords: Options, Barrier Options, Static Hedge, Binomial Tree.
Kontrak opsi saham merupakan perjanjian atau kontrak antar penjual opsi saham dengan pembeli opsi saham di mana penjual yang memberikan hak bukan suatu kewajiban kepada pembeli opsi saham untuk membeli atau menjual saham pada waktu tertentu dan harga yang telah ditentukan, apabila pada saat jatuh tempo pemegang opsi tidak menggunakan haknya maka haknya tersebut akan hilang dengan sendirinya (Tandelilin, 2010). Salah satu jenis opsi adalah opsi barrier. Opsi barrier merupakan opsi exotic yang bersifat path dependent, yang artinya nilai bergantung pada pergerakan harga saham sampai dengan waktu jatuh tempo. Pengeksekusian pada opsi barrier dilakukan tergantung pada apakah harga aset yang mendasari menyentuh barrier atau tidak selama masa hidup opsi atau selama periode waktu yang ditentukan (Hull J. , 2009). Fungsi payoff dari opsi barrier adalah fungsi diskontinu pada saat barrier disentuh dan opsi bernilai nol. Para pemegang opsi perlu melakukan strategi pengelolaan risiko untuk melindungi dana trader dari fluktuasi nilai underlying yang tidak menguntungkan. Pemegang opsi akan dapat
memaksimalkan keuntungan dan meminimalkan kerugian dari aset yang diperjualbelikan dengan melakukan hedging (lindung nilai).
Lindung nilai dapat dibagi menjadi dua yaitu static hedging (lindung nilai statis) dan dynamic hedge (lindung nilai dinamis). Lindung nilai dinamis melakukan penyeimbangan bobot pada portofolio secara terus menerus sehingga adanya biaya transaksi saat melakukan penyeimbangan portofolio. Lindung nilai statis tidak memerlukan penyeimbang sehingga biaya hedge dan transaksi menjadi satu dalam harga pasar dari opsi yang dipakai dalam lindung nilai Oleh karena itu, lindung nilai statis (static hedge) digunakan untuk menyelesaian masalah dalam lindung nilai dinamis (Derman et al., 1994).
Menghitung harga kontrak opsi dapat menggunakan model Black-Scholes. Akan tetapi untuk menghitung harga kontrak opsi yang bersifat path-dependent seperti opsi barrier memerlukan pendekatan numerik. Salah satu metode pendekatan numerik yang sering dilakukan adalah dengan the lattice methods. Metode ini terdiri dari model Binomial Tree,
model Trinomial Tree dan model Multinomial
Tree.
Model Binomial Tree merupakan salah satu
pendekatan numerik yang dapat
direpresentasikan pergerakan harga saham
memiliki dua kemungkinan pada setiap periode yaitu kemungkinan harga saham naik dan
kemungkinan harga saham turun serta dapat
digambarkan oleh garis kecil yang dibuat dari suatu node (titik) (Cox et al., 1979)
Nilai opsi beli barrier tipe Down and Out
(DOC) dihitung dengan rumus (Mendes, 2011):
DOC={0max[S
-K,0] ; St >B ; St ≤B.
(1)
Selanjutnya, nilai diskonto opsi pada waktu t dihitung dengan rumus:
Vt = ∆t(pVtu+∆t+(1-P) Vtd+ ∆t ) (2)
Pada penelitian yang dilakukan oleh Ermia et al. (2016) dalam mengestimasi harga kontrak opsi tipe amerika menggunakan metode Binomial Tree diperoleh bahwa kontrak opsi tipe Amerika dengan model Binomial Tree menggunakan variance matching pada PT. Telkomunikasi Indonesia, Tbk. harganya lebih dekat dengan perhitungan harga kontrak opsi dengan metode Black-Scholes dibandingan dengan model Binomial Tree menggunakan proporsional u∙d=1, dan risk neutral. Sedangkan pada penelitian yang dilakukan oleh Bratha et al. (2017) dalam penentuan harga kontrak opsi komoditas emas menggunakan model Binomial Tree. Penelitian tersebut didapatkan hasil bahwa perhitungan dengan model Binomial Tree pada kontrak opsi beli (call) harganya lebih murah dibandingkan dengan perhitungan metode Black-Scholes. Selain itu juga diperoleh bahwa perhitungan dengan metode Binomial Tree pada kontrak opsi jual (put) harganya lebih mahal dibandingkan dengan perhitungan metode Black-Scholes.
-
II. METODE PENELITIAN
Jenis dan Sumber Data
Jenis data yang digunakan dalam penelitian ini adalah data sekunder berupa data historis harga penutupan harian Indeks Harga Saham
Gabungan (IHSG) selama dua tahun terakhir. Dalam penelitian ini data dicatat mulai tanggal 11 Mei 2015 sampai dengan tanggal 11 Mei 2017. Penelitian ini akan mencari nilai lindung statis untuk penentuan harga kontrak opsi beli barrier tipe Down and Out dengan model Binomial Tree sebagai strategi pengelolaan risiko
Adapun langkah-langkah analisis data dalam penelitian ini adalah sebagai berikut:
-
1. Mengumpulkan data historis Indeks Harga Saham Gabungan 11 Mei 2015 sampai dengan tanggal 11 Mei 2017.
-
2. Menghitung tingkat pengembalian (return) pada waktu t(R^)dari nilai penutupan (close) saham IHSG menggunakan persamaan:
Rt =ln( St ) (3)
t=1,2,3,… , 488.
-
3. Menghitung nilai masukan deskriptif statistik yaitu rata-rata (mean), ragam (varians), kemencengan data (skewness) dan kurtosis dari data return harga saham.
-
4. Menghitung volatilitas tahunan harga opsi saham dari Indeks Harga Saham Gabungan diselesaikan dengan persamaan:
σ=√s2 ×k (4)
-
5. Menentukan nilai masukan seperti harga saham awal ( $0), harga pelaksanaan (K), waktu jatuh tempo (T), suku bunga bebas risiko (r), harga barrier (B).
-
6. Menentukan nilai pembagian periode (n) serta menghitung nilai parameter memengaruhi gerak saham naik (u), nilai parameter memengaruhi gerak saham turun (d) dan peluang harga naik (p) menggunakan persamaan (Ponte, 2013):
= u-d
-
7. Menghitung nilai saham naik dan nilai saham turun pada setiap periode dan aproksimasi nilai opsi model Binomial Tree pada Static Hedge untuk opsi beli barrier tipe Down and Out, dengan kondisi yang bersyarat yaitu (Loucks, 2010):
DOC C(K) - B P( τ ) ;b≤κ (6)
∖,c (K)-(B-K)Bdi (B)-P(K) ;B≥K dengan,
Bdi (B) =2BP (B)-^P(B)
BP (B) =N (-β)
R = —(i)(Lzf)
P σ√τ→ .
-
8. Ulangi langkah 7 dengan barrier (B) dan harga pelaksanaan (K) yang berbeda-beda.
-
9. Menghitung nilai analitik menggunakan persamaan:
nilai analitik = BqS qT (N(d1)-
b(1-N(d8))) - Ke~rτ(N(d2)-a(1-
N(d7)) (7)
-
10. Membandingkan hasil Static Hedge nilai kontrak opsi beli barrier tipe Down and Out dengan nilai analitik.
Deskripsi Data
Harga saham yang digunakan adalah penutupan harian (close price) dari Indeks Harga Saham Gabungan disajikan dalam bentuk grafik pada Gambar 1.
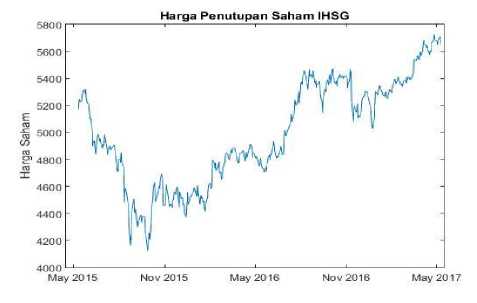
Gambar 1 Grafik Indeks Harga Saham Gabungan
Berdasarkan Gambar 4.1 dapat diamati bahwa data Indeks Harga Saham Gabungan mengalami fluktuasi pada hari-hari tertentu. Harga saham mengalami penurunan dari bulan Mei 2015 hingga Nopember 2015 kemudian mengalami kenaikan dari bulan Nopember 2015 hingga Mei 2017. Grafik selama dua tahun terakhir juga terlihat memiliki pergerakan harga saham yang cenderung meningkat.
Menghitung Tingkat Pengembalian (Return)
Nilai R t dapat dihitung menggunakan persamaan (3). Dari nilai Rt dapat nilai statistik deskriptif dari data return yaitu mean, variance, skewness, dan kurtosis yang dihitung menggunakan bantuan software Ms. Excel sehingga diperoleh hasil seperti Tabel 1 sebagai berikut:
Tabel 1 Nilai Statistik Deskriptif Data Return Indeks Harga Saham Gabungan
|
Karakteristik |
Nilai |
|
Mean |
0,00018 |
|
Variance |
0,00009 |
|
Skewness |
-0,29141 |
|
Kurtosis |
2,76698 |
Sumber: Data diolah (2018)
Berdasarkan Tabel 1 dapat dilihat bahwa rata-rata tingkat pengembalian Indeks Harga Saham Gabungan bernilai positif menunjukan bahwa adanya keuntungan. Karakteristik data memiliki bentuk yang tidak simetris hal ini ditunjukan dengan skewness yang bernilai negatif sehingga mengakibatkan data menceng ke kiri. Selanjutnya, diperoleh nilai kurtosis yang lebih kecil dibandingankan dengan nilai kurtosis yang berdistribusi normal yaitu 3 (Byrne, 2010).
Menghitung Nilai Volatilitas pada Indeks Harga Saham Gabungan
Standar deviasi dapat dipakai dengan representasi dari volatilitas dinyatakan dalam simbol σ, apabila dalam bentuk kuadrat disebut dengan variance dinyatakan dalam simbol S2. Berdasarkan data return tersebut dilakukan perhitungan untuk mencari nilai variance (S2) yang dapat dilihat pada Tabel 1. Selanjutnya volatilitas (σ) dapat dihitung sebagai berikut: σ =√S2 × k.
= √0,00009 × 246
= 0,15085.
Jadi, diperoleh volatilitas tahunan Indeks Harga Saham Gabungan sebesar 0,15085 atau 15,08%
Variabel-variabel Penentuan Harga Kontrak Opsi
Dalam penentuan lindung nilai statis pada harga kontrak opsi beli barrier tipe Down and Out menggunakan model Binomial Tree terdapat beberapa variabel yang digunakan yaitu sebagai berikut:
-
1. Menentukan nilai harga saham awal (¾)
Harga saham awal yang digunakan adalah harga penutupan Indeks Harga Saham dapat dilihat pada lampiran 1 yaitu tanggal 10 Mei 2017 sebesar 5653.
-
2. Menentukan harga pelaksanaan (K)
Harga pelaksanaan atau strike price adalah harga yang telah disepakati diawal kontrak oleh penjual dan pembeli opsi. Dalam penelitian ini harga pelaksanaan yang digunakan adalah K = 5300, K = 5400, K = 5500, K = 5600.
-
3. Menentukan waktu jatuh tempo (T)
Waktu jatuh tempo diperoleh dari lamanya kontrak opsi yaitu selama empat bulan, sehingga waktu jatuh tempo penelitian ini adalah tahun.
3
-
4. Menentukan volatilitas (σ)
Nilai volatilitas pada penelitian ini dihitung dengan menggunakan data return Indeks Harga Saham Gabungan periode 11 Mei 2015 sampai dengan 11 Mei 2017. Berdasarkan data return tersebut didapat nilai volatilitas tahunan sebesar 0,15085.
-
5. Menentukan suku bunga bebas risiko (r) Tingkat suku bunga yang digunakan dalam penelitian ini adalah suku bunga yang dikeluarkan oleh pihak berwenang yaitu Bank Indonesia sebesar 6,5%.
-
6. Menentukan nilai barrier (B)
Nilai barrier adalah nilai yang disepakati antara penjual dan pembeli opsi. Dalam penelitian ini barrier yaitu B = 3000.
Penentuan Nilai Parameter u, d dan p
Model Binomial Tree terdapat parameter memengaruhi gerak saham naik (u),
memengaruhi gerak saham turun (d) dan peluang harga saham naik (p). Nilai-nilai parameter u, d, dan p tersebut dapat dihitung
dengan nilai deskriptif statistika dari data return seperti pada Tabel 1. Berikut dipaparkan nilai-nilai variabel yang digunakan untuk menentukan nilai parameter u, d, dan p yang dapat dilihat dalam Tabel 2:
Tabel 2 Nilai-nilai Variabel Penentuan Harga Kontrak Opsi
|
Variabel |
Nilai |
|
σ |
0,15085 |
|
T |
0,33 |
|
N |
4 |
|
r |
0,065 |
|
T ∆ = n |
0,0825 |
Sumber: Data diolah (2018)
Langkah pertama dalam menentukan nilai parameter u,d dan p yaitu menghitung nilai parameter u dengan cara mensubtitusi nilai-nilai variabel yang telah diperoleh sebagai berikut: u = √∆ t
= ,15085√0,0825
= (0,15085)(0,28722 )
= ,04332
= 1,04428
Selanjutnya dapat dihitung nilai parameter d dengan dengan d = sehingga:
1
= 1,04428
= 0,95759
Setelah nilai parameter u dan d telah diperoleh, maka selanjutnya dapat dihitung nilai peluang harga saham naik p sebagai berikut:
-
er∆t-d
=
u-d
e(0, 065)( 0, 0825 ) - 0,95759
= 1,04428 - 0,95759
= 0,55119.
Peluang pergerakan saham turun dapat dihitung dengan persamaan 1-P , sehingga
1-P = 1 - 0,55119
= 0,44881.
Aproksimasi Harga Kontrak Opsi Barrier Menggunakan Model Binomial Tree
Model Binomial Tree digunakan dalam proses aproksimasi harga kontrak opsi beli barrier tipe Down and Out pada strategi lindung nilai statis dalam pengelolaan risiko.
Aproksimasi harga kontrak pada Indeks Harga Saham Gabungan dilakukan setelah mendapatkan parameter-parameter yang diperlukan lalu mengkontruksikan melalui cabang-cabang dari model Binomial Tree. Setiap node dihitung menggunakan rumus model Binomial Tree dalam perhitungan kontrak opsi beli barrier tipe Down and Out pada persamaan (1). Harga kontrak opsi beli barrier tipe Down and Out diperoleh dengan mendiskonto nilai dari simpul terakhir pada model Binomial Tree dengan menggunakan persamaan (2).
Dari data historis telah diperoleh harga saham awal ( ) sebesar 5653. Sedangkan dari
beberapa harga pelaksanaan dipilih salah satu untuk melakukan perhitungan manual yaitu sebesar 5300 dan barrier sebesar 3000. Kemudian, telah didapatka nilai parameter = 1,04428, = 0,95759, = 0,55119 dan
-
1- = 0,44881 dengan jangka waktu 4 bulan
dan menggunakan 4 periode.
Langkah yang pertama yakni menentukan nilai simpul terakhir pada C(K) (opsi call dengan strike K) digunakan persamaan sebagai berikut ( - ,0) ; >
dihitung nilai pada simpul akhir
max 0
Dari model maka dapat
, ={
secara manual sehingga diperoleh hasil sebagai berikut:
0,95759 - 5300),0)
= max((6722,76 - 5300),0) = max((1422,76),0) = 1422,76
, max((5653 × 1,04428 × 0,95759 -
5300),0)
= max((6164,72 - 5300),0)
= max(864,72,0)
= 864,722
Dengan cara yang sama seperti perhitungan , , , dapat dicari nilai untuk , , ,
Selanjutnya untuk menghitung nilai diskonto digunakan persamaan (2) sebagai berikut:
Sehingga dapat dihitung nilai diskonto secara manual untuk opsi call dengan strike K
diperoleh hasil:
= , ∙ , [0,55119 × 1422,76
+0,44881 × 864,722]
= 1166,04
Dengan cara yang sama seperti perhitungan , dapat dicari nilai untuk C2,3 C1, 3 C3,2, ..., C0,0
Langkah kedua menghitung nilai ()
(opsi put dengan ) Untuk menentukan nilai simpul terakhir pada digunakan persamaan sebagai berikut:
, ={max ( -
0
,0) ; >
; ≤
maka dapat dihitung nilai pada simpul akhir secara manual sehingga diperoleh:
0,95759),0)
= max((1698 - 6722,76),0)
= max(-5024,65,0)
=0
, = max(( - 5653 × 1,04428 ×
= max((1698 - 6164,72),0)
= max(-4466,61,0)
=0
Dengan cara yang sama seperti perhitungan , , , dapat dicari nilai untuk , , ,
Selanjutnya untuk meghitung nilai diskonto digunakan persamaan sebagai berikut:
Sehingga dapat dihitung nilai diskonto secara manual untuk opsi put dengan strike K diperoleh hasil:
= , ∙ , [0,55119×0+0,44881×0]
=0
Dengan cara yang sama seperti perhitungan , , dapat dicari nilai untuk P3,3 , P31 3, P2,2, ., P0,0
Terakhir menghitung aproksimasi lindung nilai statis untuk harga kontrak opsi beli tipe
barrier tipe Down and Out dengan model
Binomial tree menggunakan persamaan (6)
dengan B≤K sebagai berikut:
^4 ,4
'4 ,4- × ^4 ,4
1422,76
5300
×
3000
0
= 1422,76
Dengan cara yang sama seperti perhitungan , dapat dicari ⅝ ,4, ¾ ,4, ^l ,4, …, ½) ,0.
Dari perhitungan aproksimasi harga saham tersebut, diperoleh lindung nilai statis untuk opsi beli barrier tipe Down and Out dapat dibentuk Binomial Tree. Binomial Tree dapat dilihat pada Gambar 2.
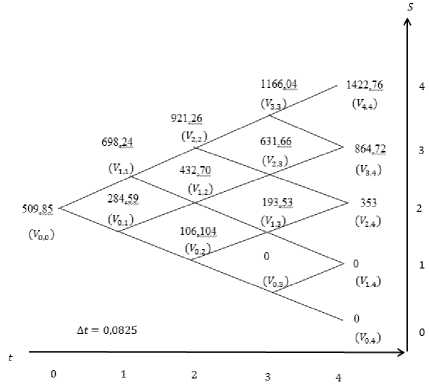
Gambar 2 Model Binomial Tree Empat Periode
Sehingga diperoleh lindung nilai statis untuk opsi beli barrier tipe Down and Out empat periode dengan harga pelaksanaan dan barrier yang ditentukan sebesar 5300 dan 3000 dalam waktu jatuh tempo selama empat bulan yaitu sebesar 509.85.
Perhitungan selanjutnya mencari aproksimasi nilai opsi dengan model Binomial Tree dihitung 2 periode, 4 periode, 10 periode, 40 periode, 80 periode dalam jangka waktu empat bulan untuk mengetahui hubungan harga pelaksanaan dengan nilai harga opsi. Penelitian ini ditetapkan harga pelaksanaan lebih besar dari barrier yaitu B = 3000 dengan K = 5300, K = 5400, K = 5500, K = 5600. Perhitungan tahapan pertama dengan mensubtitusikan nilai-nilai deskriptif
statistik dalam persamaan (9). Kemudian, menghitung lindung nilai statis menggunakan model Binomial Tree. Aproksimasi beberapa periode memerlukan perhitungan banyak sehingga perlu menggunakan software Matlab. Hasil diperoleh dalam bentuk seperti Tabel 3.
Tabel 3. Nilai Kontrak Opsi Barrier Tipe Down and Out dengan Model Binomial Tree
|
Harga Pelakasanaan (K) |
n |
Harga Opsi |
Galat |
|
5300 |
2 |
518,93 |
0,02723 |
|
4 |
509,85 |
0,00926 | |
|
10 |
504,87 |
0,00059 | |
|
40 |
505,64 |
0,00093 | |
|
80 |
505,38 |
0,00041 | |
|
5400 |
2 |
438,93 |
0,02803 |
|
4 |
435,45 |
0,01988 | |
|
10 |
427,5 |
0,00126 | |
|
40 |
427,61 |
0,00152 | |
|
80 |
427,29 |
0,00077 | |
|
5500 |
2 |
358,93 |
0,01075 |
|
4 |
361,05 |
0,01672 | |
|
10 |
359,03 |
0,01103 | |
|
40 |
354,06 |
0,00295 | |
|
80 |
355,56 |
0,00126 | |
|
5600 |
2 |
278,93 |
0,03946 |
|
4 |
286,65 |
0,01287 | |
|
10 |
290,55 |
0,00550 | |
|
40 |
291,22 |
0,00285 | |
|
80 |
290,92 |
0,00182 |
Sumber: Data diolah (2018)
Perhitungan Nilai Analitik Opsi Beli Barrier Tipe Down and Out
Nilai analitik opsi beli barrier tipe Down and Out merupakan persamaan Black-Scholes dengan adanya batasan harga (barrier). Nilai analitik diperoleh dengan mensubtitusikan nilai
, ,B,r,T dan σ ke dalam persamaan (7),
yaitu:
nilai analitik = 5653 e 0, 33 (0,8497
-
- 0,0142(1 - 1))
-
- 5300 e 0, 065 ∙0, 33 (0,8285
-
- 0,0505(1 - 1)
= 505,17
Dengan cara yang sama diperoleh nilai analitik kontrak opsi beli barrier tipe Down and Out dari setiap Harga Tebus (K) yang lainnya ditampilkan pada Tabel 4.
Tabel 4. Nilai Analitik Opsi Beli Barrier Tipe Down and Out
|
Harga Pelaksanaan (K) |
Nilai analitik opsi beli barrier tipe Down and Out |
|
5300 |
505,17 |
|
5400 |
426,96 |
|
5500 |
355,11 |
|
5600 |
290,39 |
Sumber: Data dioleh (2018)
Perbandingan Hasil Static Hedge Nilai Kontrak Opsi Beli Barrier Tipe Down and Out dengan Nilai Analitik.
Dari Tabel 3 dapat dilihat bahwa saat nilai B = 3000 pada n=80 memperlihatkan harga opsi model Binomial Tree untuk K = 5300 yaitu 505,38 mendekati nilai opsi analitik yaitu sebesar 505,17, Kemudian untuk K = 5400 harga opsi yaitu 427,29 mendekati nilai opsi analitik yaitu sebesar 426,96, selanjutnya untuk K = 5500 harga opsi yaitu 355,56 mendekati nilai opsi analitik sebesar 355,11 dan untuk K = 5600 harga opsi yaitu 290,92 mendekati nilai opsi analitik sebesar 290,39. Sehingga, dapat dinyatakan perhitungan lindung nilai statis untuk opsi beli barrier tipe Down and Out menggunakan model Binomial Tree mendekati ke nilai analitik dengan galat yang dihasilkan cukup kecil yaitu lebih kecil atau sama dengan 0,00182 untuk empat harga pelaksanaan.
IV. KESIMPULAN & SARAN
Harga opsi beli barrier tipe Down and Out menggunakan model Binomial Tree dengan harga pelaksanaan semakin besar maka semakin kecil nilai opsi. Hal ini menunjukkan hubungan harga pelaksanaan dengan harga opsi yaitu semakin jauh harga pelaksanaan dari barrier maka semakin kecil lindung nilai yang diberikan, sehingga nilai harga opsi akan semakin kecil. Berdasarkan hasil aproksimasi tersebut, galat dari harga opsi beli barrier Down and Out yang dihasilkan cukup baik karena error yang dihasilkan pada aproksimasi 80 periode cukup kecil yaitu lebih kecil atau sama dengan 0,00182 untuk empat harga pelaksanaan.
Berdasarkan hasil yang telah diperoleh, adapun saran untuk pengembangan penelitian selanjutnya diharapkan memilih barrier tipe Up and Out, Up and Out dan Down and In menggunakan The Laticce Methods lainnya seperti model Trinomial Tree, Multinomial Tree untuk menentukan harga kontrak opsi. Penentuan harga opsi dengan memasukkan faktor-faktor lain seperti suku bunga yang tidak konstan, pembagian dividen.
DAFTAR PUSTAKA
Bratha, R., Dharmawan, K., & Suciptawati, N.
L. P. 2017. Penentuan Harga Kontrak Opsi Komoditas Emas Menggunakan Metode Pohon Binomial. E-Jurnal Matematika, 6(2), pp 99-105.
Byrne, B. M. (2010). Structural Equation Modeling with AMOS: basic concepts, applications, and programming. New York: Taylor and Francis Group, LLC.
Cox, J. C., Ross, S. A., & Rubinstein, M. (1979).
Options Pricing : A Simplified Approach.
Journal of Financial Economics 7, 229-263.
Derman, E., Ergener, D., & Kani, I. 1994. Static Options Replication. Quantitative Strategies Research Note, Goldman Sachs.
Ermia, M., Dharmawan, K., & Oka. T. B. 2016.
Penerapan Metode Binomial Tree dalam Mengestimasi Harga Kontrak Opsi Tipe Amerika. E-Jurnal Matematika, 5(4),
pp.156-163.
Hull, J. 2009. Options, Future, and Others Derivatives. New Jearsey: Pearson Prentice Hall (Cox, Ross, & Rubinstein, 1979).
Loucks, J. 2010. Static Hedging. Swedia: Uppsala University.
Mendes, G. N. 2011. Valuation of Barrier Options Through Trinomial Trees. Portugal: Universidae De Lisboa.
Ponte, C. d. 2013. Pricing Barrier Options With Numerical Method. Afrika Selatan: North West University.
Tandelilin, E. 2010. Portofolio dan Investasi.
Yogyakarta: Kanisius.
363
Discussion and feedback