PEMODELAN JUMLAH TINDAK KRIMINALITAS DI PROVINSI JAWA TIMUR DENGAN ANALISIS REGRESI SPATIAL AUTOREGRESSIVE AND MOVING AVERAGE
on
E-Jurnal Matematika Vol. 7(4), November 2018, pp. 346-356
DOI: https://doi.org/10.24843/MTK.2018.v07.i04.p224
ISSN: 2303-1751
PEMODELAN JUMLAH TINDAK KRIMINALITAS
DI PROVINSI JAWA TIMUR DENGAN ANALISIS REGRESI SPATIAL AUTOREGRESSIVE AND MOVING AVERAGE
Ni Made Lasti Lispani1§, I Wayan Sumarjaya2, I Komang Gde Sukarsa3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: nimadelastilispani13@gmail.com]
-
2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
-
3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: gedesukarsa@unud.ac.id] §Corresponding Author
ABSTRACT
One of spatial regression model is spatial autoregressive and moving average (SARMA) which assumes that there is a spatial effect on dependent variable and error. SARMA can analyze the spatial effect on the higher order. The purpose of this research is to estimate the model of the total crime in East Java along with factors that affect it. The results show that the model can describe total crime in East Java is SARMA(0,1). The factors that influence the total crime are population density (X ), poverty total (X ), average length of education at every regency/city and error from the neigbors.
Keywords: total crime, spatial regression, spatial autoregressive and moving average, SARMA
Metode spasial merupakan metode yang digunakan untuk menggali informasi mengenai efek spasial pada suatu data. Hukum yang menjadi dasar dari metode spasial ini adalah hukum pertama geografis yang dikemukakan oleh Tobler yang menyatakan bahwa segala sesuatu saling berhubungan satu dengan yang lainnya, tetapi sesuatu yang dekat lebih berpengaruh daripada sesuatu yang lebih jauh (Anselin, 1988).
Seiring perkembangan analisis spasial, berkembang metode regresi spasial pada tingkat (order) yang lebih tinggi, yaitu spatial autoregressive and moving average (SARMA). SARMA adalah metode regresi spasial yang digunakan apabila diasumsikan bahwa pengaruh spasial bergantung pada variabel dependen dan sisaan. Model SARMA digunakan untuk menganalisis data cross section dengan matriks pembobot spasial sebagai bentuk hubungan antar daerah (Huang, 1984).
Tindak kriminal adalah salah satu hal yang diduga dapat dianalisis menggunakan pendekatan spasial karena pelaku tindak kriminal cenderung berpindah-pindah dari satu
wilayah ke wilayah lainnya. Menurut BPS (2017) indikator yang biasa digunakan untuk mengukur kejahatan adalah angka jumlah kejahatan (crime total), angka kejahatan per 100.000 penduduk (crime rate), dan selang waktu terjadinya suatu tindak kejahatan (crime clock). Salah satu daerah dengan jumlah tindak kriminalitas yang cukup tinggi adalah Provinsi Jawa Timur. Menurut BPS (2017), Provinsi Jawa Timur termasuk ke dalam lima provinsi dengan jumlah tindak kriminal tertinggi di Indonesia.
Tujuan dari penelitian ini adalah untuk menduga model jumlah tindak kriminalitas di Provinsi Jawa Timur dengan analisis regresi SARMA serta faktor-faktor yang memengaruhi secara signifikan.
Menurut Kutner et al. (2005), analisis regresi adalah metode statistika yang memanfaatkan hubungan antara dua atau lebih variabel kuantitatif untuk memprediksi nilai dari satu variabel respon. Adapun jenis-jenis variabel pada analisis regresi yaitu variabel tak bebas (dependen) dan variabel bebas (independen). Jika diasumsikan variabel dependen dan variabel
independen memiliki hubungan linear, maka hubungan variabel-variabel tersebut membentuk sebuah model yang disebut dengan model regresi linear. Adapun model umum analisis regresi linear dapat dinyatakan sebagai berikut.
y= +ε (1)
dengan y merupakan vektor variabel dependen berdimensi n×1,X merupakan matriks variabel independen berdimensi n×k,β menyatakan vektor parameter dari koefisien regresi yang berdimensi k×1, dan ε adalah vektor berdimensi n×1 yang menyatakan peubah acak normal bebas dan berdistribusi
identik N (0, σ2I). Salah satu metode pendugaan parameter untuk persamaan (1) adalah ordinary least square (OLS). Konsep dari metode OLS dalam menduga parameter regresi adalah meminimumkan jumlah kuadrat error. Penduga parameter β dengan metode OLS adalah sebagai berikut.
̂=(X'X)~1X,y. (2)
Salah satu bentuk pengembangan dari analisis regresi adalah analisis regresi spasial. Regresi spasial merupakan salah satu metode statistika yang digunakan untuk mengetahui hubungan antara variabel dependen dengan variabel independen dengan mempertimbangkan pengaruh spasial antardaerah. Pengaruh spasial tersebut disajikan dalam bentuk koordinat daerah atau pembobotan. Model regresi spasial dinyatakan dalam persamaan berikut (Anselin, 1988).
y= + xβ +U (3)
dengan
U= +ε (4)
dengan y menyatakan vektor variabel dependen yang berukuran n×1, X menyatakan matriks variabel independen yang berukuran n×k, β adalah vektor parameter koefisien regresi yang berukuran k×1,p merupakan koefisien spasial beda kala (lag) variabel dependen, λ adalah koefisien spasial beda kala (lag) pada error, u adalah vektor error pada persamaan (3) yang berukuran n×1, ε merupakan vektor error pada persamaan (4) berukuran n×1, yang berdistribusi normal dengan mean 0 dan varians (σ2I), I adalah matriks identitas, berukuran
n×n, 14^ = yang merupakan matriks pembobot spasial (W) berukuran n×n , dan n merupakan banyaknya pengamatan atau daerah (i=1,2,…,n) serta k adalah banyaknya parameter regresi.
Hal yang sangat penting dalam analisis spasial adalah adanya pembobot atau yang sering disebut sebagai matriks pembobot spasial. Matriks pembobot spasial digunakan untuk menentukan bobot antardaerah yang diamati berdasarkan hubungan ketetanggaan antardaerah. Menurut Anselin (1988) struktur yang mendasari ketetanggaan diungkapkan dengan bobot 0 sampai 1.
Daerah pengamatan berdasarkan sisi-sisi dan atau titik yang saling bersinggungan diberi pembobot 1, sedangkan untuk daerah lainnya diberi pembobot 0. Persinggungan tepi atau sisi disebut dengan persinggungan rook (benteng), persinggungan titik disebut dengan persinggungan bishop (menteri), dan gabungan keduanya disebut persinggungan queen (ratu). Gambar 1 merupakan ilustrasi persinggungan mengenai perhitungan matriks pembobot spasial dengan enam daerah sebagai amatannya.
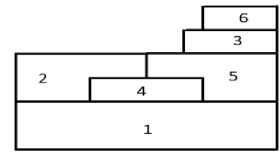
Gambar 1.Ilustrasi Persinggungan
Melalui Gambar 1 diperoleh matriks pembobot spasial tingkat pertama menggunakan persinggungan queen dengan elemen-elemen matriks yaitu : , = , =1, , = , =
-
1, W1 ,5= ,1=1, W2 ,4= ,2 =1,W2 , =
W5,2 =1, W3,5= ,3 =1, W3 ,6= ,3 =1,
, = , =1 dan pembobot yang lain sama
dengan nol. Matriks pembobot spasial tingkat pertama adalah sebagai berikut:
Diperoleh pula matriks pembobot spasial tingkat kedua menggunakan persinggungan queen
dengan elemen-elemen matriks yaitu : __ -1 __ -1 ι∣f2 _
,3= ,1=1, w2 ,3= ,2=1, w3, =
, =1, , = , =1 dan elemen
yang lainnya bernilai nol. Matriks pembobot spasial tingkat kedua adalah sebagai berikut:
001000 001 000 110100 001000 000 001 000010
Menurut LeSage (1999), transformasi sering digunakan pada penerapan matriks pembobot spasial, yaitu dengan melakukan standarisasi baris pada matriks pembobot spasial. Rumus
standarisasi baris W dengan elemen , , yaitu: ∗ _ wi,j
W ∗, i =∑ i=J , , ; (5)
dengan W ∗, j adalah nilai , yang telah
distandarisasi.
Pengembangan dari model regresi spasial adalah model regresi SARMA. Menurut Huang (1984) model regresi SARMA dibangun dari model analisis deret waktu ARMA dengan
matriks pembobot spasial W sebagai pengganti faktor waktu pada model ARMA yang menggambarkan hubungan antarlokasi. Diperlihatkan model regresi SARMA adalah sebagai berikut.
n
n
7=1
7=1
+ Θl ∑ Wi , i Zj+⋯+e, ∑ W,i , 'jεj ․
(6)
Dalam bentuk matriks diperoleh model regresi SARMA sebagai berikut.
y =∑ΦiWly + χβ +ε +∑θlWlε (7)
dengan y merupakan vektor variabel dependen
yang berukuran n×1,X adalah matriks variabel independen yang berukuran n×k,β adalah vektor parameter koefisien regresi yang berukuran k×1, Φi merupakan koefisien spasial beda kala (lag) variabel dependen pada tingkat ke- i, ^i menyatakan koefisien spasial beda kala (lag) pada error pada tingkat ke-i, ε adalah vektor error berukuran n×1, yang
berdistribusi normal dengan mean 0 dan varians (σ2I), I adalah matriks identitas, berukuran n×n, IV1 adalah matriks pembobot pada tingkat ke-i berukuran n×n dengan n merupakan banyaknya pengamatan/daerah ( = 1,2,…,n) dan k merupakan banyaknya parameter regresi.
Mengingat ε~N (0, σ2I) maka ε dapat dinyatakan dalam bentung fungsi densitas sebagai berikut.
f ( Zi)=√2πσ2 ехр[-2 σ2 ( φ )]․
Berdasarkan persamaan (8) diperoleh fungsi likelihood sebagai berikut:
L( Zi , O2)=(2πσ2) exp,- 2σ2 ( ετε)-․(9)
Berdasarkan fungsi likelihood L pada persamaan (9), dapat dinyatakan fungsi dari = (β, σ2, Φι,…,Φp , ^l ,…,Pq ) sebagai berikut:
n
L(9|y)=( ) (/)exp *- 2σ2 ( B-1 ( Ay -
√ L M Z L
Xβ))tB-1 ( Ay - Xβ)+ (10)
dengan ∖∂ε∖
J =| |=|B~1A|=|B-1|| |․
Operasi logaritma natural (ln) likelihood dari persamaan (10) dinyatakan pada persamaan berikut:
. n ~ n, ,
ln(L)=- ln2π - ln σ2 +∑ln9i +
1 2 (11)
[- 5(B~1( Ay - Xβ)) B~1( Ay - Xβ)]
dengan
Ω1 =(I -∑ ^1ΦiΛi), Ω2 =(I +∑i-ιθiΛi),
(1-∑ ‰ΦjP)
A= ΩI^, B= Ω2^, 9i = ),
Ω2 1Ω1 = diag(<91 , 92,…,9n)․ Matriks U dan V adalah matriks orthogonal yang memenuhi W= ΛV dengan ketentuan V= =
dan Λ menyatakan diag( ^-I ,A 2,… ,λn ) dengan λn merupakan nilai-nilai eigen dari matriks W. Adapun pendugaan parameter model regresi SARMA adalah sebagai berikut.
-
a. Penduga Parameter β
Pendugaan parameter β , dilakukan dengan menurunkan fungsi pada persamaan (11) secara
parsial terhadap β dan menyamakannya dengan nol. Diperoleh nilai penduga parameter β adalah sebagai berikut:
£ = (Xτ (B BtY1 Xy rXτ (B BtY1 Ay. (12)
-
b. Penduga Parameter σ2
Pendugaan parameter , dilakukan dengan menurunkan fungsi pada persamaan (11) secara parsial terhadap dan menyamakannya dengan nol. Diperoleh nilai penduga parameter untuk adalah sebagai berikut:
-
σ2 =^AyYMA y (13)
dengan
M = (BBtY 1 - (BBτY1X(Xt(BBτY 1XY 1Xτ(BBτY 1
-
c. Penduga Parameter
Menurut Huang (1984) penduga φ dan θ diperoleh dengan meminimumkan fungsi berikut:
2
F (θ, )) = nσ YHYg g)~. (14)
Pendugaan parameter diperoleh dengan
menurunkan persamaan (14) secara parsial terhadap dan menyamakannya dengan nol. Diperlukan iterasi numerik Davidon-Fletcher-Powell dalam pendugaaan parameter φ.
-
d. Penduga Parameter
Pendugaan parameter diperoleh dengan menurunkan persamaan (14) secara parsial terhadap θ dan menyamakannya dengan nol. Diperlukan iterasi numerik Davidon-Fletcher-Powell dalam pendugaaan parameter .
Sebelum memodelkan suatu data menggunakan analisis spasial, perlu diselidiki ada atau tidaknya kebergantungan spasial pada data tersebut. Anselin (1988) menyatakan bahwa uji yang digunakan untuk menguji kebergantungan spasial pada suatu data adalah uji Lagrange Multiplier (LM). Adapun jenis-jenis uji LM diperlihatkan pada Tabel 1.
Tabel 1. Uji Lagrange Multiplier
|
Statistik Uji |
Keputusan |
|
[ετWy∕(^)]2 LMiag = L d n i dengan : H0 tφ = 0 H1 -.φ≠0 |
Hipotesis null dapat ditolak jika nilai LMiag > X2a, 1 |
|
r T i 2 [ετWε∕(^)] = ---— e rr tr (W2 + WτW) dengan : H0 tθ = 0 H1 ^ ≠0 |
Hipotesis null dapat ditolak jika nilai LMen > X2, 1 |
|
LM(lag, err) = E~ iRyYT - 2RyRεT + (RεY(D+T) dengan : H0 : φ d nn θ = 0 H1: φ nnn θ ≠ 0 |
Hipotesis null dapat ditolak jika nilai LM(iag,err) > Y2 λ a, 2 |
dengan = γ^)YYAxyγγ^γγ
tr (W2 + WτW), ε menyatakan vektor sisaan dari OLS, β adalah penduga parameter yang diperoleh dengan metode OLS, σ2 menyatakan adalah kuadrat tengah sisaan dari model OLS, dan tr adalah operator teras matriks (penjumlahan elemen diagonal suatu matriks), Ry = ^, R =-^Y = tr tr{(W' + W)W}, D = σ((W, XβVM(W' Xβ),
M = I- X(X'Xy 1 X,l E = (D + DT - (T)2.
Pada analisis deret waktu, fungsi autokorelasi (ACF) digunakan untuk mengidentifikasi model yang tepat dalam pendugaan model. Begitu pula pada analisis spasial, koefisien autokorelasi spasial menunjukkan kekuatan autokorelasi spasial dari unit spasial pada tingkat tertentu. Fungsi autokorelasi spasial pada tingkat ke- l dinyatakan dengan rumus sebagai berikut:
= 3iL ∑io∑2=o(Λ-y)(y∕^vMj (15)
p () n + 1-r ∑τi=0(yl-yY
dengan p(l) merupakan koefisien autokorelasi spasial pada tingkat ke- l, n adalah jumlah amatan, adalah nilai variabel dependen pada amatan ke- i., y merupakan rata-rata nilai variabel dependen dan w-j adalah nilai bobot antara amatan ke- dan ke- pada tingkat ke- .
Uji Signifikansi dari koefisien autokorelasi spasial di setiap tingkat dapat ditentukan dengan suatu selang sebagai berikut:
̂(I)-Za√1/n ≤ ̂(I)≤ ̂(I)+Za√1/n (16) 2 2
Koefisien autokorelasi dinyatakan signifikan pada taraf nyata a apabila pada selang yang diperoleh tidak memuat nilai nol.
Pemilihan model terbaik dilakukan untuk mendapatkan model yang paling baik dari beberapa model yang terbentuk. Ada beberapa kriteria dalam menentukan model terbaik. Kriteria pemilihan model terbaik yang digunakan dalam penelitian ini adalah Akaike’s Information Criterion (AIC). AIC dirumuskan sebagai berikut (Anselin, 1988).
AIC=-2L+2k (17)
dengan L merupakan nilai maksimum ln likelihood, k merupakan banyaknya parameter dalam model. Model yang dipilih berdasarkan kriteria AIC adalah model yang memiliki nilai AIC paling kecil.
Menurut Gujarati (2009), ada beberapa asumsi yang menjadi dasar dalam pembentukan model analisis regresi linear sederhana. Adapun asumsi-asumsi tersebut adalah asumsi
kenormalan sisaan (uji Anderson-Darling), tidak terdapat autokorelasi antar sisaan (uji Bruesh-Godfey), asumsi homoskedastik (uji Bruesh-Pagan), dan tidak terdapat multikolinearitas
(nilai VIF < 5).
Pengujian signifikansi pendugaan parameter
model dilakukan untuk mengetahui peranan variabel independen dalam menjelaskan variabel dependen pada model. Pengujian signifikansi parameter pada penelitian ini menggunakan uji
Wald (Hq : ,θ,β =0). Statistik uji yang
digunakan adalah sebagai berikut.
(18)
Wald =
se(r)
dengan r menyatakan nilai penduga suatu
parameter yang diperoleh dan se(r) menyatakan standar error dari penduga parameter r.
Hipotesis null yang menyatakan bahwa parameter tidak signifikan dapat ditolak jika
nilai Wald > Za .
2
Data yang dipergunakan dalam penelitian ini berupa data sekunder. Data diperoleh dari Badan Pusat Statistik Indonesia dan Badan Pusat Statistik Provinsi Jawa Timur. Unit observasi (amatan) yang digunakan dalam penelitian ini adalah setiap kabupaten/kota di Provinsi Jawa Timur pada tahun 2016, yaitu sebanyak 38 kabupaten/kota.
Variabel yang digunakan dalam penelitian adalah variabel dependen (y) berupa jumlah tindak kriminalitas di setiap kabupaten/kota di Jawa Timur dan variabel independen pada penelitian ini meliputi kepadatan penduduk di setiap kabupaten/kota di Jawa Timur ( ^l ), jumlah penduduk miskin di setiap kabupaten/kota di Jawa Timur ( %2 ) dan rata-rata lamanya sekolah di setiap kabupaten/kota di Jawa Timur ( ^3).
Metode dan tahapan analisis yang digunakan dalam penelitian ini adalah sebagai berikut:
-
a. Melakukan eksplorasi data untuk
-
b. mengetahui penyebaran pada setiap variabel dari sudut kewilayahan dengan
menggunakan peta tematik.
-
c. Melakukan pendugaan parameter β dan pemodelan regresi linear dengan metode ordinary least square (OLS).
-
d. Melakukan pengujian asumsi analisis regresi pada model regresi linear yang diperoleh dengan metode OLS.
-
e. Jika terdapat autokorelasi pada model regresi linear, lakukan uji kebergantungan spasial dengan tahapan sebagai berikut.
-
- Menentukan matriks pembobot spasial
(W) tingkat pertama dengan menggunakan metode persinggungan queen.
-
- Uji kebergantungan spasial dengan menggunakan Uji Langrange Multiplier.
Jika tidak terdapat autokorelasi, maka pemodelan dilanjutkan dengan pemodelan regresi linear dengan metode OLS.
-
f. Identifikasi model SARMA melalui fungsi autokorelasi spasial dengan langkah-langkah sebagai berikut.
-
- Menentukan matriks pembobot spasial ( wz ) menggunakan metode persinggungan queen pada order yang lebih tinggi.
-
- Menghitung koefisien autokorelasi dari setiap tingkat spasial berdasarkan fungsi autokorelasi spasial pada persamaan (18) dan menguji signifikansinya dengan persamaan (19).
Beberapa model regresi SARMA dapat dibentuk dengan memperhatikan koefisien autokorelasi yang signifikan.
-
g. Melakukan pemodelan regresi SARMA dengan tahapan sebagai berikut.
-
- Melakukan pendugaan parameter untuk model regresi SARMA dengan maximum likelihood estimation (MLE).
-
- Pemilihan model terbaik dengan kriteria AIC (Akaike’s information criterion). Model yang terbaik adalah model yang memiliki nilai AIC paling kecil.
-
- Pengujian asumsi-asumsi analisis regresi pada model SARMA yang terpilih.
-
- Pengujian signifikansi setiap parameter pada model regresi SARMA yang terpilih menggunakan uji Wald.
-
h. Menginterpretasikan dan menyimpulkan hasil yang diperoleh.
Pada penelitian ini angka yang menunjukkan banyaknya kejadian dari setiap variabel digambarkan dalam sebuah peta tematik. Peta tematik merupakan sebuah peta khusus yang menyajikan tema tertentu yang berfungsi untuk menambah informasi, sehingga memudahkan pembaca dalam membaca peta. Setiap variabel akan dikategorikan menjadi tiga kategori yaitu rendah, sedang dan tinggi. Warna daerah yang semakin gelap menunjukkan semakin tinggi nilai dari variabel tersebut. Gambar 2 menunjukkan penyebaran jumlah tindak kriminalitas di Provinsi Jawa Timur tahun 2016.
Terdapat 33 kabupaten/kota yang termasuk dalam kategori jumlah tindak kriminalitas rendah (99 - 1279). Kabupaten dengan jumlah tindak kriminalitas terendah adalah Kabupaten Pacitan yaitu sebanyak 99 kejadian. Terdapat empat kabupaten pada kategori jumlah tindak kriminalitas sedang (1280 - 3805) dan satu
kabupaten pada kategori jumlah tindak kriminalitas tinggi (3806 - 7817), yaitu Kota Surabaya. Jumlah tindak kriminalitas di Kota Surabaya sebanyak 7.817 kejadian.
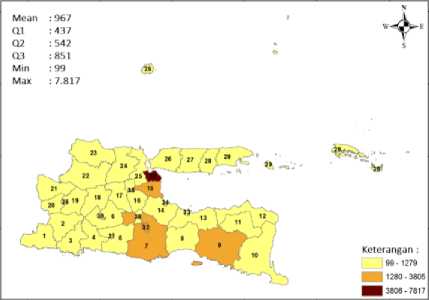
Gambar 2. Peta Spasial Jumlah Tindak Kriminalitas Provinsi Jawa Timur Tahun 2016
Selanjutnya, penyebaran kepadatan penduduk dari setiap kabupaten/kota di Provinsi Jawa Timur pada Tahun 2016 ditunjukkan pada Gambar 3.
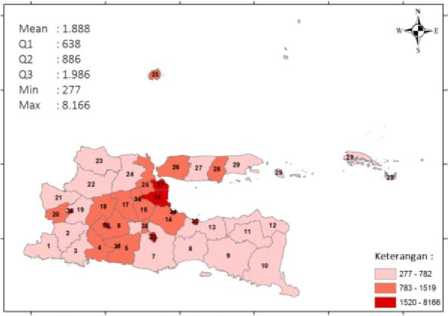
Gambar 3. Peta Spasial Kepadatan Penduduk di Provinsi Jawa Timur Bedasarkan Kabupaten/Kota Tahun 2016
Pada tahun 2016 kepadatan penduduk di Jawa Timur adalah sebesar 817 jiwa/km2. Kabupaten/Kota yang termasuk dalam kategori tingkat kepadatan penduduk rendah adalah sebanyak 17 kabupaten/kota dengan nilai terendah adalah 397 jiwa/km2 yaitu terdapat di kabupaten Pacitan. Terdapat 12 kabupaten/kota yang termasuk dalam kategori kepadatan penduduk sedang dan 9 kabupaten/kota masuk dalam kategori tingkat penduduk tinggi. Kepadatan penduduk tertinggi terdapat di Kota Surabaya, yaitu sebesar 8.166 jiwa/km2.
Penyebaran jumlah penduduk miskin dari setiap kabupaten/kota di Provinsi Jawa Timur pada tahun 2016 diperlihatkan pada Gambar 4.
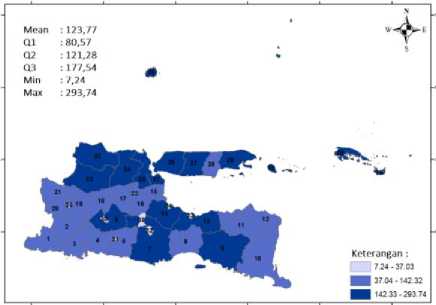
Gambar 4. Peta Spasial Jumlah Penduduk Miskin di Provinsi Jawa Timur Bedasarkan
Kabupaten/Kota Tahun 2016
Jumlah penduduk miskin di Provinsi Jawa Timur pada tahun 2016 adalah sebanyak 4.703.300 jiwa. Terdapat delapan kabupaten/kota yang termasuk dalam kategori jumlah penduduk miskin rendah (7,24 -37,03). Jumlah penduduk miskin yang terendah adalah Kabupaten Mojokerto, yaitu sebanyak 7.240 jiwa. Tujuh belas kabupaten/kota masuk ke dalam kategori sedang (37,04 - 142,32) dan 13 kabupaten/kota lainnya masuk dalam kategori jumlah penduduk miskin tinggi (142,33 - 293,74). Kabupaten/Kota dengan jumlah penduduk miskin tertinggi adalah Kabupaten Malang, yaitu sebanyak 293.740 jiwa.
Gambar 5 menunjukkan penyebaran rata-rata lamanya sekolah dari setiap kabupaten/kota di Provinsi Jawa Timur pada tahun 2016.
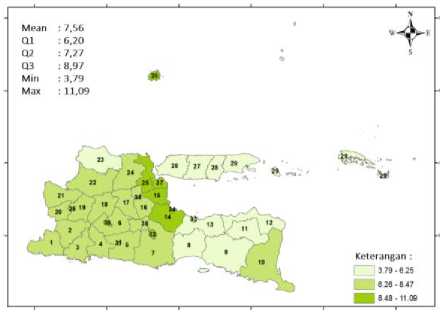
Gambar 5. Peta Spasial Rata-rata Lamanya Sekolah di Provinsi Jawa Timur Bedasarkan
Kabupaten/Kota
Pada Gambar 5, terdapat sepuluh kabupaten/kota yang masuk dalam kategori rata-rata lamanya sekolah rendah (3,79 - 6,25). Kabupaten Sampang adalah kabupaten dengan nilai rata-rata lamanya sekolah terendah, yaitu selama 3,79 tahun. Terdapat 18 kabupaten/kota yang masuk dalam kategori sedang (6,26 - 8,47) dan sepuluh kabupaten/kota lainnya masuk dalam kategori tinggi (8,48 - 11,09) dengan Kota Madiun memiliki nilai yang tertinggi, yaitu 11,09 tahun.
Estimasi model regresi linear dilakukan menggunakan metode OLS. Diperoleh estimasi model regresi linear seperti pada Tabel 2.
Tabel 2. Estimasi Parameter Model Regresi Linear
|
Parameter |
Estimasi Paramete r |
Standar Error |
^■hitung |
Pvalue |
|
βo |
-3․221,323 |
1․176,273 |
-2,739 |
0,009 |
|
0,374 |
0,114 |
3,281 |
0,002 | |
|
β2 |
11,922 |
2,549 |
4,676 |
0,000 |
|
β3 |
265,507 |
149,147 |
1,780 |
0,084 |
|
R2 = 54,660 % | ||||
Sumber : Data diolah, 2018
Diperoleh estimasi model regresi linear berdasarkan Tabel 2 adalah sebagai berikut: ̂i = -3․221,323+0,374X1,i +11,922X2,i
+265,507X , ․
Pengujian asumsi-asumsi persamaan (19) diperlihatkan pada Tabel 3.
Tabel 3. Uji Asumsi Model Regresi Linear
|
Jenis Uji |
Hipotesis Uji |
Nilai Kritis |
Keputusan |
|
Anderson-Darling |
¾ : Sisaan mengikuti sebaran normal ^1 : Sisaan tidak mengikuti sebaran normal |
AD = 0,863 co ,05 = 0,730 |
H0 ditolak |
|
Bruesch-Godfrey |
Wq : Tidak terdapat autokorelasi Wi : Terdapat autokorelasi |
BG = 2,998 x(0,05), 1 = 3,841 |
H0 tidak dapat ditolak |
|
Bruesch-Pagan |
Wq : Ragam homogen Wi : Ragam tidak homogen |
BP = 21,766 Y2 (0,05), 3 = 7,815 |
H0 ditolak |
|
Uji Multiko-linearitas |
y I Fi>5 : Terdapat multikolinearita s |
VIF1 = 2,457 VIF2 = 1,560 VIF3 = 2,752 |
Tidak terdapat Multiko-linearitas |
Sumber : Data diolah, 2018
Uji Bruesch-Godfrey dan uji Bruesch-Pagan mengasumsikan bahwa sisaan pada model telah mengikuti sebaran normal, sedangkan pada Tabel 3 diperoleh keputusan uji Anderson-Darling adalah Hq ditolak yang artinya sisaan tidak mengikuti sebaran normal. Sehingga keputusan uji Bruesch-Godfrey dan uji Bruesch-Pagan pada Tabel 3 dapat dinyatakan belum akurat. Salah satu cara untuk mengatasi masalah pelanggaran asumsi-asumsi tersebut adalah melakukan transformasi pada data. Jenis transformasi data yang akan digunakan dapat ditentukan dengan memperhatikan nilai λ pada model regresi Box-Cox (lihat Gujarati, 2009, hal.187).
Diperoleh estimasi parameter λ untuk data jumlah tindak kriminalitas di Provinsi Jawa Timur adalah -0,216. Hasil estimasi tersebut mendekati nilai nol, sehingga data akan ditransformasi dalam bentuk log natural (ln). Tabel 4 menunjukkan hasil estimasi parameter regresi pada data yang telah ditransformasi.
Tabel 4. Estimasi Parameter Regresi pada Data yang Telah Ditransformasi
|
Paramete r |
Estimasi Paramete r |
Standar Error |
^hitung |
Pvalue |
|
β∗ |
-4,411 |
1,377 |
-3,203 |
0,002 |
|
β∗ |
0,586 |
0,153 |
3,836 |
0,001 |
|
β∗ |
0,771 |
0,111 |
6,969 |
0,000 |
|
β∗ |
1,641 |
0,552 |
2,975 |
0,005 |
|
R2 = 63,870% | ||||
Sumber: Data diolah, 2018
Diperoleh estimasi model regresi linear pada data yang telah ditransformasi adalah sebagai berikut:
ln ̂l=-4,411+0,585lnX1,i+0,771lnX2,i
+1,6418 ln X , ․ ,
Selanjutnya dilakukan pengujian asumsi-asumsi regresi linear untuk persamaan (20) yang dapat dilihat pada Tabel 5.
Diperlihatkan bahwa masih terdapat pelanggaran asumsi autokorelasi. Objek yang menjadi amatan pada penelitian ini berupa wilayah kabupaten/kota di Provinsi Jawa Timur (amatan spasial), sehingga diduga masih terdapat autokorelasi spasial dalam model pada persamaan (20). Oleh karena itu, analisis akan dilanjutkan dengan pengujian kebergantungan spasial.
Tabel 5. Uji Asumsi Model Regresi pada Data yang Telah Ditransformasi
|
Jenis Uji |
Hipotesis Uji |
Nilai Kritis |
Keputusan |
|
Anderson-Darling |
¾ : Sisaan mengikuti sebaran normal #1 : Sisaan tidak mengikuti sebaran normal |
AD = 0,208 co,05 = 0,730 |
H0 tidak dapat ditolak |
|
Bruesch-Godfrey |
Hq : Tidak terdapat autokorelasi Hi : Terdapat autokorelasi |
BG = 5,112 Y2 (o,05), 1 = 3,841 |
H0 ditolak |
|
Bruesch-Pagan |
Hq : Ragam homogen H1 : Ragam tidak homogeny |
BP = 4,674 Y2 (o,05), 3 = 7,815 |
H0 tidak dapat ditolak |
|
Uji Multiko-linearitas |
VlFi>5 : Terdapat multikolinearitas |
VIF1 = 2,738 VlF2 = 1,881 VlF2 = 2,398 |
Tidak terdapat Multiko-linearitas |
Sumber : Data diolah, 2018
Pengujian kebergantungan spasial dapat dilakukan dengan uji Lagrange Multiplier. Sebelum melakukan uji kebergantungan spasial, terlebih dahulu dibentuk matriks pembobot spasial tingkat pertama. Matriks pembobot spasial dibentuk menggunakan metode queen.
Tabel 6. Hasil Uji Lagrange Multiplier
|
Jenis Uji |
Nilai Kritis |
Nilai Statistik Uji |
Keputusan |
|
Kebergantungan spasial pada variabel dependen |
3,841 |
0,488 |
H0 tidak dapat ditolak |
|
Kebergantungan spasial pada sisaan |
3,841 |
4,085 |
H0 ditolak |
|
Kebergantungan spasial pada variabel dependen dan sisaan |
5,991 |
6,156 |
H0 ditolak |
Sumber : data diolah, 2018
Tabel 6 menunjukkan hasil dari uji Lagrange Multiplier. Diperlihatkan bahwa terdapat kebergantungan spasial pada variabel dependen dan sisaan sehingga pemodelan dapat dilanjutkan dengan model analisis regresi SARMA.
Fungsi autokorelasi digunakan untuk mengidentifikasi model yang tepat dalam analisis regresi SARMA. Pembentukan fungsi autokorelasi spasial memerlukan matriks pembobot spasial pada tingkat yang lebih tinggi. Matriks pembobot spasial yang dapat dibentuk
adalah matriks pembobot spasial hingga tingkat ke-7. Tabel 7 menunjukkan koefisien-koefisien autokerelasi dari setiap tingkat spasial serta selang signifikansinya.
Tabel 7. Koefisien-Koefisien Autokorelasi Spasial
|
Jenis Autokorelasi |
Tingkat Spasial ke- |
Koefisien |
Interval |
|
Pada Variabel Dependen |
1 |
0,250 |
(-0,024;0,524) |
|
2 |
0,029 |
(-0,244;0,304) | |
|
3 |
0,016 |
(-0,258;0,291) | |
|
4 |
-0,009 |
(-0,283;0,265) | |
|
5 |
-0,021 |
(-0,295;0,253) | |
|
6 |
-0,213 |
(-0,487;0,061) | |
|
7 |
-0,025 |
(-0,299;0,248) | |
|
Pada Sisaan |
1 |
0,283 |
(0,009;0,558) |
|
2 |
0,112 |
(-0,161;0,386) | |
|
3 |
0,021 |
(-0,253;0,295) | |
|
4 |
-0,123 |
(-0,397;0,151) | |
|
5 |
-0,035 |
(-0,309;0,238) | |
|
6 |
0,051 |
(-0,223;0,325) | |
|
7 |
-0,065 |
(-0,339;0,209) |
Sumber : Data diolah, 2018
-
b. Pemilihan Model Terbaik
Pemilihan model terbaik dilakukan dengan melihat nilai AIC. Model yang dipilih adalah model dengan nilai AIC terendah.
Tabel 9. Nilai AIC Masing-masing Model SARMA
|
Model SARMA |
Nilai AIC |
|
SARMA(0,1) |
60,385 |
|
SARMA(1,0) |
64,343 |
|
SARMA(1,1) |
60,664 |
Sumber: Data diolah, 2018
Pada Tabel 9 diperoleh model dengan nilai AIC terendah adalah model regresi SARMA(0,1). Sehingga model yang dipilih untuk dianalisis selanjutnya adalah model SARMA(0,1).
-
c. Pengujian Asumsi Model SARMA(0,1)
Hasil pengujian asumsi-asumsi model SARMA(0,1) dapat dilihat pada Tabel 10.
Pada Penelitian ini dihitung koefisien-koefisien autokorelasi pada variabel dependen serta pada sisaan dari setiap tingkat spasial. Jika pada selang signifikansi tidak memuat nilai 0, maka koefisien autokorelasi signifikan pada tingkat tersebut. Diperlihatkan bahwa interval yang tidak memuat nilai 0 adalah interval koefisien korelasi pada sisaan tingkat pertama, sehingga pemodelan yang dilakukan adalah pemodelan SARMA pada tingkat pertama.
-
a. Pendugaan Parameter Model Regresi
SARMA
Pendugaan parameter regresi SARMA diperoleh dengan metode maximum likelihood estimator (MLE). Pada Tabel 8 diperlihatkan tiga model SARMA yang dapat dibentuk pada tingkat pertama. Satu dari tiga model tersebut akan dipilih sebagai model terbaik dengan menggunakan kritera AIC.
Tabel 8. Penduga Parameter Model Regresi
SARMA
|
Parameter |
Estimasi | ||
|
SARMA(0,1) |
SARMA(1,0) |
SARMA(1,1) | |
|
β∗ |
-4,912 |
-4,779 |
-4,684 |
|
β∗ |
0,769 |
0,582 |
0,845 |
|
β∗ |
0,798 |
0,752 |
0,714 |
|
β∗ |
1,179 |
1,474 |
0,885 |
|
Φl |
- |
0,124 |
0,009 |
|
0,427 |
- |
0,477 | |
|
R2 |
71,148% |
65,541% |
72,612% |
Sumber : Data diolah, 2018
Tabel 10. Pengujian Asumsi Model SARMA (0,1)
|
Jenis Uji |
Hipotesis Uji |
Nilai Kritis |
Keputusa n |
|
Anderson-Darling |
Hq : Sisaan mengikuti sebaran normal H^ : Sisaan tidak mengikuti sebaran normal |
AD = 0,302 co,05 = 0,730 |
H0 tidak dapat ditolak |
|
Bruesch-Godfrey |
H0 : Tidak terdapat autokorelasi H1 : Terdapat autokorelasi |
BG = 0,128 Y2 (o,05), 1 ∖ = 3,841 |
H0 tidak dapat ditolak |
|
Bruesch-Pagan |
Hq : Ragam homogen H-^ : Ragam tidak homogen |
BP = 3,978 Y2 (o,05), 3 ∖ = 7,815 |
H0 tidak dapat ditolak |
|
Uji Multiko-linearitas |
VIF1>5 : Terdapat multikolineari-tas |
VIF1 = 2,737 VIF2 = 1,881 VIF3 = 2,398 |
Tidak terdapat Multiko-linearitas |
Sumber : data diolah, 2018
Hasil pengujian asumsi model SARMA(0,1) menunjukkan bahwa model regresi SARMA(0,1) memenuhi asumsi-asumsi analisis regresi linear. Oleh karena itu, model regresi
SARMA(0,1) layak digunakan untuk menduga model jumlah tindak kriminalitas di Provinsi Jawa Timur.
-
d. Uji Signifikansi Parameter
Pengujian signifikansi parameter digunakan untuk menyelidiki peranan variabel-variabel independen dalam menjelaskan variabel dependen. Uji yang dapat digunakan untuk menguji signifikansi parameter adalah uji Wald yang ditunjukkan pada Tabel 11.
Tabel 11. Uji Wald Model Regresi SARMA (0,1)
|
Parameter |
Estimasi Parameter |
Standar Error |
Wald |
Pvalue |
|
β∗ |
-4,912 |
1,391 |
-3,531 |
0,000 |
|
β∗ |
0,769 |
0,150 |
5,117 |
0,000 |
|
β∗ |
0,798 |
0,103 |
7,740 |
0,000 |
|
β∗ |
1,177 |
0,547 |
2,153 |
0,031 |
|
0,427 |
0,196 |
2,183 |
0,033 |
Sumber: data diolah, 2018
Diperlihatkan bahwa terdapat pengaruh spasial yang signifikan pada sisaan serta variabel ^l , variabel ^2 , dan variabel ^3 memengaruhi variabel y secara signifikan. Sehingga diperoleh model terbaik adalah sebagai berikut: ln ̂i=-4,912+0,769ln , +0,798ln ,
+1,179lnχ3 , l +0,427,∑ "=1 ,I≠i Wι∣̂ , (21)
dengan ̂i adalah penduga jumlah tindak
kriminalitas pada kabupaten/kota ke-i, Xj
merupakan jumlah tindak kriminalitas pada kabupaten/kota ke-j, , adalah nilai bobot
spasial pada kabupaten/kota ke-i dan ke-j, ,
adalah kepadatan penduduk pada kabupaten/kota ke- i, , adalah jumlah warga miskin pada
kabupaten/kota ke-i, , adalah rata-rata lama
sekolah pada kabupaten/kota ke-i , dan ̂ adalah sisaan ke-j dari model SARMA(0,1).
Berdasarkan analisis regresi SARMA yang dilakukan untuk memodelkan jumlah tindak kriminalitas di Provinsi Jawa Timur, diperoleh model yang terbaik adalah model SARMA(0,1). Ketiga variabel independen menunjukkan pengaruh positif yang signifikan terhadap jumlah tindak kriminalitas di Provinsi Jawa Timur setelah dilakukan transformasi log natural pada data. Pengaruh variabel yang paling
dominan memengaruhi jumlah tindak kriminalitas di Provinsi Jawa Timur pada tahun 2016 adalah rata-rata lamanya sekolah, yaitu sebesar 1,177, artinya jika nilai log natural dari rata-rata lamanya sekolah di suatu kabupaten/kota naik 1 nilai, maka dapat menaikkan nilai log natural dari jumlah tindak kriminalitas di kabupaten/kota tersebut sebesar 1,177 apabila faktor lain dianggap konstan.
Variabel jumlah penduduk miskin memberikan pengaruh sebesar 0,798 yang artinya jika nilai log natural dari jumlah warga miskin di suatu kabupaten/kota naik 1 nilai, maka dapat menaikkan nilai log natural dari jumlah tidak kriminalitas di kabupaten/kota tersebut sebesar 0,798 apabila faktor lain dianggap konstan.
Variabel kepadatan penduduk memengaruhi jumlah tindak kriminalitas sebesar 0,769 yang artinya jika nilai log natural dari tingkat kepadatan penduduk di suatu kabupaten/kota naik 1 nilai, maka dapat menaikkan nilai log natural dari jumlah tidak kriminalitas di kabupaten/kota tersebut sebesar 0,769 apabila faktor lain dianggap konstan.
Kenaikan nilai rata-rata lamanya sekolah diharapkan mampu menurunkan jumlah tindak kriminalitas, namun dalam estimasi model SARMA(0,1) menunjukkan hasil yang tidak sesuai harapan, dimana rata-rata lamanya sekolah justru berpengaruh positif terhadap jumlah tindak kriminalitas. Hal tersebut dapat disebabkan oleh berbagai faktor, salah satunya diduga karena tindak kriminalitas mulai melibatkan penduduk yang menempuh pendidikan lebih tinggi baik sebagai korban atau pelaku tindak kriminal. Penelitian lebih lanjut perlu dilakukan untuk menganalisis masalah tersebut.
Selain variabel-variabel tersebut, diperoleh pula hasil bahwa terdapat interaksi spasial sebesar 0,427 pada sisaan antarkabupaten/kota yang berhubungan melalui persinggungan titik dan sisi. Setiap kabupaten/kota memiliki model SARMA (0,1) yang berbeda-beda, hal ini bergantung pada nilai pembobot spasial (W ) dari kabupaten/kota yang berhubungan. Sebagai contoh Kabupaten Pacitan yang mempunyai
model SARMA(0,1) sebagai berikut.
lnŷKab ․Pacitan=-4,912+0,769lnX1, Kab ․Pacitan
+0,798lnX2, Kab ․Pacitan +1,177lnX3, Kab ․Pacitan + 0,427(0,5)̂εKab․Ponorogo + 0,427(0,5)̂εKab․Trenggalek
-
4. KESIMPULAN DAN SARAN
Berdasarkan hasil dan pembahasan yang telah diperolah, dapat dijabarkan beberapa kesimpulan sebagai berikut.
-
a. Pada jumlah tindak kriminalitas di Provinsi Jawa Timur pada tahun 2016, terdapat kebergantungan spasial antarkabupaten/kota pada variabel dependen serta pada sisaan model, sehingga pemodelan dilakukan menggunakan metode regresi spasial yaitu model SARMA. Terdapat kebergantungan spasial pada sisaan tingkat pertama dan dipilih model SARMA(0,1) sebagai model terbaik dengan nilai AIC sebesar 60,385. Model SARMA (0,1) yang terbentuk untuk memodelkan jumlah tindak kriminalitas di Provinsi Jawa Timur pada tahun 2016 adalah sebagai berikut:
ln ̂l=-4,912+0,769ln , +0,798ln , +1,177 ln X3 ,i+0,427,∑ , ̂
dengan koefisien determinasi (R2) sebesar 71,163%, artinya model mampu menjelaskan jumlah tindak kriminalitas di Provinsi Jawa Timur sebesar 71,163%, sedangkan sisanya dijelaskan oleh variabel lain diluar model.
-
b. Faktor yang berpengaruh secara signifikan terhadap jumlah tindak kriminalitas di Provinsi Jawa Timur pada tahun 2016 adalah faktor tingkat kepadatan penduduk di setiap kabupaten/kota di Provinsi Jawa Timur, jumlah penduduk miskin di setiap kabupaten/kota Provinsi Jawa Timur dan rata-rata lamanya sekolah di setiap kabupaten/kota Provinsi Jawa Timur.
Saran yang dapat diberikan untuk penelitian selanjutnya adalah sebagai berikut.
-
a. Nilai dari R2 yang diperoleh belum cukup tinggi sehingga disarankan untuk mempertimbangkan kelinearan model dan penambahan variabel independen.
-
b. Menggunakan matriks pembobot spasial yang berbeda sebagai perbandingan.
DAFTAR PUSTAKA
Anonim. 2018. Kamus Besar Bahasa Indonesia (Online). https://kbbi.web.id/kriminalitas, diakses pada tanggal 23 April 2018.
Anselin, L. 1988. Spatial Econometrics: Methods and Models. The Netherlands: Kluwer Academic Publishers.
Anselin, L. dan Smirnov, O. 1996. Efficient Algorithms for Constructing Proper Higher Order Spatial Lag Operators. Journal of Regional Science, Volume 36, Nomor 1, hlm 67 – 89.
BPS. 2017. Statistik Kriminal 2017. Jakarta : Badan Pusat Statistik.
BPS Provinsi Jawa Timur. 2017. Provinsi Jawa Timur Dalam Angka 2017. Jawa Timur: Badan Pusat Statistik.
Gujarati, D. N. dan Porter D. C. 2009. Basic Econometrics. New York: McGraw-Hill.
Huang, J. S. 1984. The Autoregressive Moving Average Model for Spatial Analysis. Austral. J. Statist., Volume 26, Nomor 2, hlm 169 – 178.
Kutner, M. H., Nachsheim, C. J., Neter, J. dan Li, W. 2005. Applied Linear Statistical Models (Fifth ed.). New York: McGraw-Hill.
LeSage, J. P. 1999. The Theory and Practice of Spatial Econometrics. Department of Economics: University of Toledo.
4.2 Saran
356
Discussion and feedback