PENDEKATAN REGRESI SPLINE UNTUK MEMODELKAN POLA PERTUMBUHAN BERAT BADAN BALITA
on
E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 259-263
DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p212
ISSN: 2303-1751
PENDEKATAN REGRESI SPLINE UNTUK MEMODELKAN POLA PERTUMBUHAN BERAT BADAN BALITA
Ni Luh Sukerni1, I Komang Gde Sukarsa2, Ni Luh Putu Suciptawati3
1Program Studi Matematika, FMIPA – Universitas Udayana [Email: sukeerni@gmail.com] 2Program Studi Matematika, FMIPA – Universitas Udayana [Email:gedesukarsa@unud.ac.id] 3Program Studi Matematika, FMIPA – Universitas Udayana [Email:suciptawati@unud.ac.id]
ABSTRACT
The study is aimed to estimate the best spline regression model for toddler’s weight growth patterns. Spline is one of the nonparametric regression estimation method which has a high flexibility and is able to handle data that change in particular subintervals so thus resulting in model which fitted the data. This study uses data of toddler’s weight growth at Posyandu Mekar Sari, Desa Suwug, Kabupaten Buleleng. The best spline regression model is chosen based on the minimum Generalized Cross Validation (GCV) value. The study shows that the best spline regression model for the data is quadratic spline regression model with six optimal knot points. The minimum GCV value is 0,900683471925 with the determination coefficient (R2) equals to 0,954609.
Keywords: GCV, Knot points, Nonparametric Regression, Spline, Toddler’s Weight
Pendekatan nonparametrik digunakan untuk mengetahui pola hubungan antara variabel respon dengan variabel prediktor yang bentuk fungsinya tidak diketahui. Pendekatan nonparametrik tidak terikat oleh asumsi-asumsi tertentu seperti sisaan berdistribusi normal dan memiliki variansi yang konstan. Bentuk kurva hanya diasumsikan bersifat mulus (smoothness) di mana data akan mencari sendiri bentuk estimasinya. Terdapat beberapa pendekatan dalam regresi nonparametrik (Hardle, 1994) di antaranya histogram, penduga kernel, penduga spline, deret Fourier, dan lain-lain.
Regresi spline mempunyai fleksibilitas yang tinggi dan mampu menangani data yang perilakunya berubah–ubah pada sub–sub interval tertentu (Eubank, 1999). Spline merupakan potongan polinomial (piecewise polynomial) dengan sifat tersegmen yang terbentuk pada titik-titik knot. Titik knot merupakan titik perpaduan bersama yang terjadi karena terdapat perubahan pola perilaku data. Terdapat beberapa metode untuk memilih titik knot yang optimal dalam regresi nonparametrik
spline antara lain metode cross validation (CV), unbiassed risk (UR), generalized cross validation (GCV), dan generalized maximum likelihood (GML).
Metode yang digunakan untuk menentukan titik knot optimal pada penelitian ini adalah generalized cross validation (GCV) dengan kriteria GCV minimum (Wahba, 1990). Penggunaan titik knot pada penelitian ini dibatasi sebanyak sepuluh titik knot.
Salah satu kasus yang menggunakan penduga spline dalam menduga model regresi adalah kasus pertumbuhan balita. Pemantauan pertumbuhan pada balita dapat dilakukan dengan cara mengukur berat badan pada balita. Pola pertumbuhan pada balita cenderung memiliki perubahan perilaku pada umur-umur tertentu, sehingga penduga spline merupakan metode yang sesuai untuk melihat dan memantau pertumbuhan berat badan pada balita. Penelitian ini bertujuan untuk mengestimasi model regresi spline terbaik pada pola pertumbuhan berat badan balita di Posyandu Mekar Sari, Desa Suwug, Kabupaten Buleleng.
Secara umum, model regresi nonparametrik dapat dituliskan sebagai berikut:
yi = f (Xi)+ εii i = 1,2,...,n (1)
dengan yi menyatakan variabel respon dari data ke-i , xt menyatakan variabel prediktor dari data ke-i, f(x= menyatakan fungsi regresi yang tidak diketahui bentuknya, dan menyatakan error ke-i yang diasumsikan menyebar N ~(0,σ2 ).
Fungsi spline berorde p adalah sebarang fungsi yang dapat ditulis dalam bentuk:
Vi — βo + βι× t + " + βpX f
K
+ ∑β++k(x - K k++ + ε i k=i
Σ β jxi + Σ [βp+k-
dengan fungsi sepenggal (truncated) sebagai berikut:
( (Xi - Kk)p>
(x —k k)+= Iun tuk x i ≥ k k
\ 0, Xt < κk
dengan j j adalah konstanta real dan
k 1 ,κ2, ...,κk adalah titik-titik knot.
Fungsi spline dapat disajikan dalam bentuk matriks yang dituliskan sebagai berikut:
Y = Xβ + ε
dengan
yi y2
yn.
r β° i
βι
βp βr .β(p+ky
(3)
ε1
ε2
£ = ⋮ ,
ε∏.
(X1 - K) )+ (X2 - K) )+
( - )
Untuk mencari nilai penduga β digunakan metode least square. Metode ini dilakukan dengan meminimumkan terhadap
(Draper & Smith, 1992).
ετε — (Y -Xβ) (Y -Xβ)
= YτY - 2βτXtY - (4)
XτβτXβ.
Kemudian meminimumkan persamaan (4) dengan menurunkan terhadap β sama dengan 0.
XτXβ —XtXY
Sehingga diperoleh nilai β sebagai berikut: β = (XτX)- 1XtY (5)
Bentuk penduga dari fungsi Y dapat dituliskan sebagai berikut:
Y — X(XtX) ~ 1Xt (6)
Titik knot optimal dipilih berdasarkan kriteria generalized cross validation (GCV) yang minimum. Rumus untuk menghitung GCV adalah sebagai berikut:
MSE (k)
GCV (k) — r 1 /,λ1λ7 (7)
(n~ttr[I - A(k])22
dengan MSE)=- n~ 1∑ "^(yi-^)2, n
adalah jumlah data, I adalah matriks identitas, k
adalah titik knot ( , , ,., ) dan A (k) — X(XτX) Xt (Eubank, 1999).
Setelah diperoleh model regresi spline terbaik, selanjutnya dilakukan pengujian parameter model. Pengujian parameter model terdiri dari dua tahapan, yaitu pengujian secara serentak kemudian dilanjutkan dengan pengujian secara individu. Uji serentak dilakukan untuk mengetahui signifikansi parameter model regresi secara bersama-sama (Neter et al., 1997a). Hipotesis yang digunakan pada uji serentak adalah sebagai berikut:
Hq: βl — β2 — "' — P++k - 0,
m i n i ma I ad a s a tu βj ≠ 0,j :
— 1,2, ..,p + k
dengan nilai p+k adalah jumlah parameter dalam model regresi spline, p adalah derajat pada spline dan k adalah jumlah knot. Statistik uji yang digunakan adalah uji F:
phitmg ssr ∕db
— SSE/db
Tolak H0 jika
Fh i tung > F a((++k'), n-(k+k') - 1 ).
Pengujian parameter secara
(8)
nilai
individu
bertujuan untuk mengetahui mana variabel yang berpengaruh secara signifikan terhadap model
(Neter et al., 1997a). Hipotesis yang digunakan dalam uji individu adalah sebagai berikut:
Ho: βj = 0
H1: βj≠O ; y = 1,2.....p + k
Statistik uji yang digunakan adalah uji t:
β
^h i tung = ^^~) (9)
dengan daerah kritis tolak Hj jika ∖t hitung∖ > i(Ξn^p+k-)-^ dengan n merupakan jumlah pengamatan dan (p+k) merupakan jumlah parameter dalam model regresi spline.
-
2. METODE PENELITIAN
Jenis dan Sumber Data
Data yang digunakan adalah data rekam berat badan balita yang diambil di Posyandu Mekar Sari, Desa Suwug, Kabupaten Buleleng. Variabel respon (Y) pada penelitian ini adalah berat badan balita saat ditimbang dalam satuan kg. Variabel prediktor dalam penelitian ini adalah berat badan balita saat lahir dalam satuan kilogram (X1) dan umur balita saat ditimbang dalam satuan bulan (X2).
Metode Analisis Data
Langkah analisis dalam penelitian ini adalah sebagai berikut:
-
1. Mengidentifikasi pola hubungan antara variabel respon (Y) dengan variabel prediktor (X1) serta (X2) menggunakan scatter plot.
-
2. Memodelkan hubungan variabel prediktor (X1) dan (X2) terhadap variabel respon (Y) dengan regresi spline satu knot sampai sepuluh knot untuk masing-masing orde linearr, kuadratik, kubik.
-
3. Menentukan titik knot optimal dengan kriteria Generalized Cross Validation (GCV) minimum.
-
4. Menetapkan model regresi spline terbaik.
-
5. Melakukan uji signifikansi parameter
secara serentak dan individu.
-
6. Menginterpretasikan model regresi spline terbaik dan menarik kesimpulan dari model.
-
3. HASIL DAN PEMBAHASAN
Scatterplot untuk Variabel Respon dengan Variabel Prediktor
Scatterplot of Berat Saat Ini (kg) vs Berat Lahir (kg)
£ S n n (n
n £
14
12
10
8
6
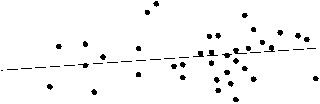
2.00 2.25 2.50 2.75 3.00 3.25 3.50 3.75
Berat Lahir (kg)
Gambar 1. Scatterplot antara Berat Badan Balita saat
Lahir (X1) dengan Berat Badan Balita saat Ditimbang ( k)
Scatterplot of Berat Saat Ini (kg) vs Umur (bulan)
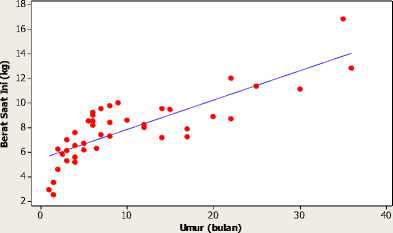
Gambar 2. Scatterplot antara Umur Balita saat Ditimbang (X2) dengan Berat Badan Balita saat Ditimbang ( k)
Pola hubungan antara setiap variabel prediktor dengan variabel respon memiliki pola yang tidak mengikuti pola tertentu sehingga sulit didekati dengan pendekatan regresi parametrik.
Estimasi Model Regresi Spline Terbaik
Pemilihan model regresi spline terbaik dipengaruhi oleh lokasi dan banyaknya titik knot. Lokasi titik knot yang berbeda akan menghasilkan model yang berbeda. Pemilihan titik knot optimal berdasarkan kriteria GCV minimum. Berikut ini merupakan tabel yang menunjukkan titik-titik knot yang optimal, nilai GCV minimum serta orde yang optimal untuk setiap variabel.
Tabel 1. Nilai GCV Minimum untuk Masing-masing Titik Knot
|
Titik knot |
Nilai GCV minimum |
Orde | |
|
X1 |
X2 | ||
|
1 titik knot |
1,455221 |
kubik |
kubik |
|
2 titik knot |
1,328506 |
kuadratik |
kuadratik |
|
3 titik knot |
0,9947627 |
kubik |
kubik |
|
4 titik knot |
0,9910701 |
kuadratik |
kuadratik |
|
5 titik knot |
0,9173034 |
kuadratik |
kuadratik |
|
6 titik knot |
0,9006834 |
kuadratik |
kuadratik |
|
7 titik knot |
1,0140267 |
kuadratik |
kuadratik |
|
8 titik knot |
1,1362618 |
linear |
linear |
|
9 titik knot |
1,2691636 |
linear |
linear |
|
10 titik knot |
1,5345317 |
linear |
linear |
Tabel 1 menunjukkan bahwa nilai GCV minimum diperoleh untuk model dengan enam titik knot pada orde kuadratik. Titik knot pada X1 adalah K1 = 1,8878; K2 = 2,081622; K3 = 2,275444; κ4 = 2,6630889 ;
K5 = 2,85691111 ;K6 = 3,05073333. Titik knot pada X2 adalah κ4 = 1,35; κ2 = 5,16111; κ3 = 8,9722222; K4 = 16,594444; = 20,4055556; κ6 = 24,2166667.
Nilai estimasi parameter ̂ yang diperoleh untuk regresi spline orde kuadratik dengan 6 titik knot adalah sebagai berikut:
-0,156245062553979
⎡ 0,100550364394037 ⎤ ⎢-1,108564002538701⎥
1,52722226563398
-0,577515588303437 0,100833839676168
⎢-0,045746458863910⎥ ⎢0,0016664516812001⎥
⎢-0,086243375517550⎥ ⎢ 0,032517164203101⎥
⎢-0,032660375867682⎥ ⎢ 0,000082183735415⎥
⎢-0,000346005761766⎥
Selanjutnya dilakukan uji signifikansi parameter regresi nonparametrik spline secara serentak dengan hipotesis sebagai berikut:
:
minimal ada satu βj≠0,j =1,2,…,16
Tabel 2. Analisis Varians Regresi Nonparametrik Spline
|
Sumber |
db |
SS |
MS |
hitung |
|
Regresi |
15 |
280,90 |
18,72 |
37,45 |
|
Error |
26 |
13,12 |
0,5 | |
|
Total |
41 |
294,02 |
Dengan menggunakan α = 0,05, maka diperoleh nilai F tabel sebesar 2,07 sehingga Tabel 2 menunjukkan bahwa nilai Khitung > Ktabel . Hal ini mengindikasikan bahwa H0 ditolak, yang artinya terdapat pengaruh yang signifikan secara bersama-sama antara variabel bebas terhadap variabel respon pada model regresi nonparametrik spline. Kemudian dilakukan uji parameter secara individu dengan menggunakan uji t. Hasil pengujian signifikansi parameter model secara individu yang disajikan pada Tabel 3.
Tabel 3. Hasil Uji Individu Parameter Model Regresi Nonparametrik Spline
|
Variabel |
Parameter |
t-hitung |
t-tabel |
Keputusan |
|
X1 |
Pl |
-5,18 |
2,05954 |
Tolak |
|
P2 |
6,48 |
Tolak | ||
|
Pl |
-7,02 |
Tolak | ||
|
P4 |
6,84 |
Tolak | ||
|
Ps |
-5,96 |
Tolak | ||
|
P6 |
2,14 |
Tolak | ||
|
P7 |
-0,94 |
Gagal Tolak | ||
|
Ps |
0,07 |
Gagal Tolak | ||
|
X2 |
P9 |
-3,17 |
Tolak | |
|
PlO |
3,19 |
Tolak | ||
|
Pll |
-3,18 |
Tolak | ||
|
Pl2 |
0,65 |
Gagal Tolak | ||
|
Pi2 |
1,22 |
Gagal Tolak | ||
|
P14 |
0,82 |
Gagal Tolak | ||
|
PlS |
-2,15 |
Tolak | ||
|
P16 |
3,02 |
Tolak |
Dengan menggunakan tingkat signifikansi α = 5% didapatkan parameter-parameter yang signifikan yaitu βl , β2 , β3 , β4 , β5 , β6 , βg , βlθ , βll , βl5 , βl6 ․ Meskipun terdapat beberapa parameter yang tidak signifikan pada model, namun semua variabel bebas berpengaruh terhadap pola pertumbuhan berat badan balita.
Berikut merupakan estimasi model regresi nonparametrik spline pada orde kuadratik dengan 6 titik knot optimal yaitu:
̂= -0,1562450625539 xl
+ 0,100550364394037 Xi
-1,108564002538701 (Xi - 1,8878) i
+1,52722226563398 (Xi - 2,0816222) i
-0,577515588303437 (Xi
- 2,2754444) i
+0,100833839676168 (Xi - 2,66308889)i
-0,04574645886391 (Xi - 2,85691111) i
+0,0016664516812001 (Xi - 3,05073333)i
-0,08624337551755 X2
+ 0,0325171642031 χ22
-0,032660375867682 (X2 - 1,35) i
+0,000082183735415 (χ2 - 5,161111) i
+0,000079441422929 (χ2 - 8,9722222) i
+0,000090794244481 (χ2 - 16,5944444)i
-0,000346005761766 (χ2 - 20,4055556)i
+0,00029106019013 (χ2 - 24,2166667)i
Estimasi model regresi nonparametrik spline yang terbaik pada kasus pertumbuhan berat badan balita adalah model regresi spline dengan orde optimal kuadratik dengan 6 titik knot pada masing-masing variabel prediktor. Nilai GCV minimum yang dihasilkan adalah 0,900683471925 serta koefisien determinasi (R2) sebesar 0,954609. Hal ini menunjukkan bahwa regresi nonparametrik spline dapat memodelkan hubungan antara berat badan balita saat lahir (X1) dan umur balita saat ditimbang (X2) terhadap berat badan balita saat ditimbang (Y) dengan baik.
Untuk penelitian selanjutnya saran yang dapat penulis sampaikan untuk penelitian lebih lanjut dengan pendekatan regresi nonparametrik yang lain regresi kernel. Penentuan orde pada setiap variabel dalam regresi spline tidak harus sama melainkan bisa berbeda-beda untuk setiap variabel.
DAFTAR PUSTAKA
Draper, N. R., & Smith, H. (1992). Analisis Regresi Terapan, diterjemahkan oleh Bambang Sumantri. Jakarta: PT. Gramedia Pustaka Utama.
Eubank, R. (1999). Spline Smoothing and Nonparametric Regression. New York: Marcell Dekker.
Hardle,W. (1994). Applied Nonparametric Regression.New York: Cambridge
University Press.
Neter, J., Wasserman, W., & Kutner, M. H. (1997a). Model Linier Terapan I : Analisis Regresi Linier Sederhana. Terjemahan Bambang Sumantri. Bogor: Jurusan
Statistika FMIPA IPB.
Wahba, G. (1990). Spline Models for Observational Data. CBMS-NSF Regional Conference Series in Applied Mathematics, 59.
263
Discussion and feedback