MENYELESAIKAN VEHICLE ROUTING PROBLEM MENGGUNAKAN ALGORITMA FUZZY EVOLUSI
on
E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 252-258
DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p211
ISSN: 2303-1751
MENYELESAIKAN VEHICLE ROUTING PROBLEM MENGGUNAKAN ALGORITMA FUZZY EVOLUSI
I Putu Arya Yoga Sumadi1§, I Putu Eka Nila Kencana2, Luh Putu Ida Harini3
1Program studi Matematika, Fakultas MIPA – Universitas Udayana [Email: yoga.sumadi87@gmail.com]
2Program studi Matematika, Fakultas MIPA – Universitas Udayana [Email: i.putu.enk@unud.ac.id]
3Program studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ballidah@unud.ac.id]
§Corresponding Author
ABSTRACT
The purpose of this research is to know the performance of Fuzzy Evolutionary Algorithm in solving one type of Vehicle Routing Problem that is Capacitated Vehicle Routing Problem (CVRP). There are 8 different CVRP data to be solved. The performance of the algorithm can be determined by comparing the value obtained by AFE with the optimal value of the data. The result of this research is fuzzy evolution algorithm yields the best average relative error from all data for distance that is equal to 69,5855% and for minimum vehicle equal to 26%.
Keywords: Vehicle Routing Problem, Fuzzy Evolutionary Algorithm, Genetic Algorithm, Fuzzy Logic
Vehicle Routing Problem (VRP) merupakan permasalahan combinatorial optimization yang termasuk dalam kategori NP-Hard Complete. Permasalahan inti dari VRP adalah menentukan rute terpendek yang dilakukan beberapa kendaraan dalam proses pengiriman barang dan menentukan kelompok konsumen yang akan dilayani oleh setiap kendaraan tersebut sedemikian sehingga menghasilkan biaya pengiriman terendah. Dalam perkembangannya VRP memiliki berbagai macam varian dalam segi kendalanya seperti mempertimbangkan jendela waktu, depot lebih dari satu, kapasitas kendaraan yang berbeda-beda, dan lain-lain. Namun setiap varian tersebut merupakan perluasan dari model dasar VRP yaitu Capacitated Vehicle Routing Problem (CVRP).
Seiring dengan perkembangan zaman, berbagai pendekatan baru telah berkembang dalam menyelesaikan masalah CVRP. Salah satu pendekatan tersebut adalah Algoritma Genetika (AG). Beberapa penelitian mengenai CVRP yang diselesaikan menggunakan AG telah banyak dilakukan. Salah satunya dilakukan oleh
Áslaug Sóley Bjarnadóttir pada tahun 2004 dengan judul Solving The Vehicle Routing Problem with Genetic Algorithms. Penelitian ini menunjukkan perancangan AG dengan menggunakan beberapa jenis operator crossover berbeda memberikan hasil yang belum cukup baik daripada Algoritma Tabu Search dan Hybrid AG.
Penelitian lain dilakukan oleh Ikhsan Hidayat mahasiswa dari UNY pada tahun 2016. Penelitian yang berjudul “Penerapan Algoritma Genetika pada Penyelesaian Capacitated Vehicle Routing Problem (CVRP) untuk Distribusi Surat Kabar Kedaulatan Rakyat di Kabupaten Sleman” memperoleh kesimpulan yaitu Algoritma AG mendapatkan hasil yang lebih baik dengan jarak tempuh 133,7 km dan waktu tempuh 198 menit daripada penelitian sebelumnya yang menggunakan algoritma Sweep dengan jarak tempuh sebesar 142,9 km dan waktu tempuh 210 menit.
Dalam perkembangannya, AG memiliki beberapa kelemahan dalam pencarian solusi optimum. Salah satu hal yang mempengaruhi adalah penggunaan parameter yang kurang tepat
dalam menyelesaikan suatu kasus pada algoritma tersebut. Inilah yang menyebabkan AG sering terjebak dalam kondisi nilai optimum lokal (Xu & Vukovich, A Fuzzy Genetic Algorithm with Effective Search and Optimization, 1993). Salah satu solusi mengurangi kemungkinan terjadinya kondisi tersebut adalah menggabungkan AG dengan logika fuzzy. Dalam beberapa penelitian gabungan dua metode ini disebut dengan nama Algoritma Fuzzy Evolusi (AFE).
Dalam tahapan penyelesaian masalah, AFE menggunakan alur yang sama seperti pada algoritma genetika, yang membedakannya adalah penentuan parameter-parameter yang digunakan dalam algoritma fuzzy evolusi menggunakan sistem fuzzy. Namun belum diketahui bagaimana kinerja dan tahapan yang digunakan AFE dalam menyelesaikan CVRP. Berdasarkan penjelasan tersebut, penulis ingin mencoba menyelesaikan masalah CVRP dengan menggunakan AFE.
Model VRP yang paling dasar adalah CVRP dan digunakan sebagai acuan dalam membangun model jenis VRP yang lainnya. Model CVRP mempunyai beberapa parameter yaitu (Bjarnadóttir, 2004):
-
1. mewakili jumlah konsumen
-
2. mewakili jumlah permintaan dari
konsumen ke
-
3. mewakili biaya atau jarak atau waktu
tempuh yang diperlukan untuk bepergian dari konsumen ke konsumen
Semua parameter tersebut mempunyai nilai yang non-negatif. Setiap kendaraan diasumsikan sama berangkat dari satu depot tunggal yang disimbolkan dengan vertek 0 dan akan mengirimkan barang ke himpunan konsumen
={1,2,.., }. Setiap konsumen akan dilayani
oleh tepat satu kendaraan yang memiliki tepat satu rute dan setiap kendaraan mengawali dan mengakhri perjalanannya di depot. Jumlah permintaan konsumen dalam setiap rute tidak boleh melebihi kapasitas kendaraan dalam rute tersebut. Fungsi objektif dalam kasus ini adalah meminumkan biaya atau kuantitas lain yang
cocok untuk masalah dalam kasus yang akan diselesaikan.
Model matematika permasalahan VRP dapat direpresentasikan menggunakan graph =
( , ) dengan vertek ={0}∪ dan busur ={( , )∈ × } dengan asumsi graph
lengkap. Setiap busur dalam A misalkan ( , ), mempunyai biaya perjalanan sebesar dan
diasumsikan = serta =0. Himpunan
semua kendaraan adalah ={1,2,… } dan
memiliki kapasitas sebesar . Satu-satunya variabel keputusan dalam kasus ini adalah sebagai berikut:
⎩0,
Jika kendaraan k bergerak dari konsumen i. ke konsumen j
Jika lainnya
(1)
Fungsi objektif dari model matematika tersebut adalah
∑∑∑ (2)
∈ ∈ ∈
Dengan fungsi kendala, yaitu:
|
∑∑ =1 |
∀ ∈ |
(3) |
|
∈ ∈ ∑ ∑ ≤ |
∀ ∈ |
(4) |
|
∈ ∈ ∑ =1 |
∀ ∈ |
(5) |
|
∈ ∑ -∑ =0 ∈ ∈ |
∀ ∈ ∀ ∈ |
(6) |
∈ {0,1}, ∀( , )∈ ∀ ∈ (7)
Persamaan 3 memastikan setiap konsumen dilayani oleh tepat satu kendaraan dan setiap kendaraan melalui tepat satu busur setelah melayani konsumen ke maupun berawal dari depot. Persamaan 4 adalah kendala kapasitas kendaraan. Jumlah permintaan konsumen tidak melebihi dari kapasitas kendaraan yang melayani konsumen tersebut. Persamaan 5 memastikan setiap kendaraan hanya bisa meninggalkan depot tepat satu kali sedangkan persamaan 6 adalah kendala yang memastikan jumlah kendaraan yang melayani setiap
DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p211
konsumen dan kembali ke depot sama dengan jumlah kendaraan yang berangkat.
Algoritma Fuzzy Evolusi (AFE) adalah sebuah teknik gabungan antara AG dengan Logika Fuzzy. Tahapan atau alur dari metode ini hampir sama dengan AG. Perbedaannya terletak pada penggunaan parameter kontrol dalam AG yang biasanya ditentukan oleh pengguna, sedangkan pada AFE ditentukan menggunakan aturan dalam logika fuzzy. Tahapan dari AFE adalah sebagai berikut :
-
1. Teknik penyandian atau representasi kromosom
-
2. Prosedur inisialisasi atau inisialisasi populasi 3. Penentuan parameter, yaitu parameter kontrol yang diperoleh dari proses sistem fuzzy
-
4. Fungsi evaluasi
-
5. Seleksi
-
6. Crossover
-
7. Mutasi
-
8. Elitisme
Dalam makalah ini model yang digunakan adalah model yang dikemukakan oleh Xu dan Vukovich pada tahun 1993 dan 1994. Penentuan parameter dari model ini menggunakan FIS metode Mamdani. Metode mamdani dalam model Xu menggunakan dua buah masukkan dan dua buah keluaran. Dua masukkan yang digunakan adalah jumlah populasi yang digunakan dan generasi yang akan diproses. Sedangkan dua keluaran yang diperoleh adalah nilai probabilitas Crossover dan nilai probabilitas Mutasi.
Terdapat Sembilan aturan yang dikembangkan dalam model Xu yaitu:
-
1. IF (Generation is SHORT) AND (Population
is SMALL) THEN (ProbCrossover is
MEDIUM) AND (ProbMutation is LARGE)
-
2. IF (Generation is SHORT) AND (Population is MEDIUM) THEN (ProbCrossover is SMALL) AND (ProbMutation is MEDIUM)
-
3. IF (Generation is SHORT) AND (Population is LARGE) THEN (ProbCrossover is SMALL) AND (ProbMutation is SMALL)
-
4. IF (Generation is MEDIUM) AND (Population is SMALL) THEN (ProbCrossover is LARGE) AND (ProbMutation is MEDIUM)
-
5. IF (Generation is MEDIUM) AND (Population is MEDIUM) THEN (ProbCrossover is LARGE) AND (ProbMutation is SMALL)
-
6. IF (Generation is MEDIUM) AND (Population is LARGE) THEN (ProbCrossover is MEDIUM) AND (ProbMutation is VERY SMALL)
-
7. IF (Generation is LONG) AND (Population is SMALL) THEN (ProbCrossover is VERY LARGE) AND (ProbMutation is SMALL)
-
8. IF (Generation is LONG) AND (Population is MEDIUM) THEN (ProbCrossover is VERY LARGE) AND (ProbMutation is VERY SMALL)
-
9. IF (Generation is LONG) AND (Population is LARGE) THEN (ProbCrossover is LARGE) AND (ProbMutation is VERY SMALL)
Sembilan aturan yang telah diberikan akan diimplementasikan dalam FIS mamdani. Namun perlu diperhatikan, agar keluaran dari FIS mamdani menghasilkan nilai atau hasil tentunya perlu dibuatkan semesta pembicaraan dan domain yang menentukan batasan-batasan nilai untuk semua himpunan yang ada pada setiap variabel. Misakan nilai untuk semesta pembicaraan pada variabel generasi adalah [0 500], yang berarti bahwa variabel generasi mempunyai semesta pembicaraan dengan nilai dari 0 sampai dengan 500. Sedangkan misal domain untuk himpunan SMALL pada variabel generasi adalah [50 100], yang berarti bahwa generasi dikatakan small jika memiliki nilai antara 50 dan 100. Aturan nilai untuk semesta pembicaraan dan domain dalam penelitian ini menggunakan nilai batas yang dikemukan oleh Sri Hartati dan Shofwatul ‘Uyun (2011) dengan fungsi keanggotaan yang digunakan adalah kurva-S dan kurva lonceng PI. Nilai batas dan fungsinya adalah sebagai berikut:
-
1. Aturan nilai Variabel Populasi adalah
-
a. Semesta pembicaraan : [0 150]
-
b. Domain SMALL : [0 75]
-
c. Domain MEDIUM : [30 120]
-
d. Domain LARGE : [75 150]
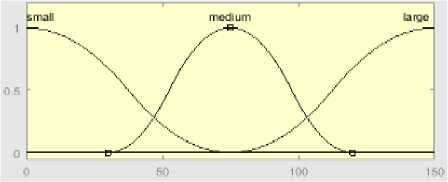
Gambar 1. Semesta pembicaraan dan domain untuk variabel Populasi (Hartati & Uyun, 2011)
-
2. Aturan nilai Variabel Generasi adalah
-
a. Semesta pembicaraan : [0 1500]
-
b. Domain SHORT : [50 530]
-
c. Domain MEDIUM : [250 1250]
d. Domain LONG : [970 1450]
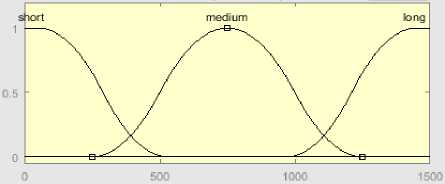
Gambar 2. Semesta pembicaraan dan domain untuk variabel Generasi (Hartati & Uyun, 2011)
-
3. Aturan nilai Variabel Probabilitas Crossover
adalah
-
e. Domain VERY LARGE : [0.65 0.95]
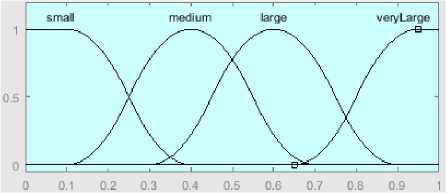
Gambar 3. Semesta pembicaraan dan domain untuk variabel Probabilitas Crossover (Hartati & Uyun, 2011)
-
4. Aturan nilai Variabel Probabilitas Mutasi adalah
-
a. Semesta pembicaraan : [0 01]
-
b. Domain VERY SMALL : [0.1 0.4]
-
c. Domain SMALL : [0.1 0.7]
-
d. Domain MEDIUM
-
e. Domain LARGE
: [0.3 0.9]
: [0.65 0.95]
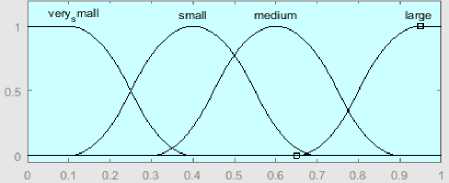
Gambar 4. Semesta pembicaraan dan domain untuk variabel Probabilitas Mutasi (Hartati & Uyun, 2011)
Jenis data yang digunakan dalam penelitian ini berupa data kuantitatif. Sumber data yang digunakan yaitu data sekunder. Adapun data sekunder yang digunakan adalah data benchmark yang terdiri dari delapan data set berbeda dan disediakan pada web : http://vrp.atd-lab.inf.puc-rio.br/.
Analisa dilakukan dengan menghitung nilai relative error parameter tiap data dan rata-rata relative error keseluruhan data untuk mengetahui kinerja AFE dalam menyelesaikan masalah CVRP secara umum. Kemudian akan disimpulkan hasil dari penelitian ini.
Terdapat delapan data berbeda yang digunakan untuk proses uji coba pada AFE dalam menyelesaikan permasalahan CVRP. Data-data tersebut disajikan pada Tabel 1.
Dalam penelitian ini, perangkat lunak yang digunakan untuk mendapatkan hasil dari AFE dalam menyelesaikan CVRP adalah Matlab R2017a. Sedangkan untuk inputan yang diberikan pada AFE yaitu berupa populasi sebesar 50, 100 dan 150 dan generasi sebesar 200, 500, 750, 1250, dan 1500. Sehingga dalam satu data uji, akan dilakukan sebanyak 15 kali percobaan dengan menggunakan kombinasi populasi dan generasi yang berbeda-beda.
Tabel 1. Data Uji Coba
|
No |
Data |
Deskripsi |
|
1 |
P-n16-k8 |
Data set yang diteliti oleh Augerat et al. pada tahun 1995 dengan jumlah konsumen 15, kendaraan optimum 8 buah dan kapasitas kendaraaan sebesar 35 unit. |
|
2 |
E-n22-k4 |
Data set yang diteliti oleh Gaskell pada tahun 1967 dengan jumlah konsumen 21, kendaraan optimum 4 buah dan kapasitas kendaraan sebesar 6000 unit. |
|
3 |
B-n31-k5 |
Data set yang diteliti oleh Augerat et al. pada tahun 1995 dengan jumlah konsumen 30, kendaraan optimum 5 buah dan kapasitas kendaraan sebesar 100 unit. |
|
4 |
A-n32-k5 |
Data set yang diteliti oleh Augerat et al. pada tahun 1995 dengan jumlah konsumen 31, kendaraan optimum 5 buah dan kapasitas kendaraan sebesar 100 unit. |
|
5 |
F-n45-k4 |
Data set yang diteliti oleh Fisher pada tahun 1994 dengan jumlah konsumen 44, kendaraan optimum 4 buah dan kapasitas kendaraan sebesar 2010 unit. |
|
6 |
CMT1 |
Data set yang diteliti oleh Christofides et al. pada tahun 1979 dengan jumlah konsumen 50, kendaraan optimum 5 buah dan kapasitas kendaraan sebesar 160 unit. |
|
7 |
Tai75a |
Data set yang diteliti oleh Rochat and Taillard pada tahun 1995 dengan jumlah konsumen 75, kendaraan optimum 10 buah dan kapasitas kendaraan 1445 unit. |
|
8 |
X-n101-k25 |
Data set yang diteliti oleh Uchoa, Pecin, Pessoa, Poggi, Vidal, & Subramanian pada tahun 2016 dengan jumlah konsumen 100, kendaraan optimum 25 buah dan kapasitas kendaraan sebesar 206 unit. |
Sumber: (Uchoa, Pecin, Pessoa, Poggi, Vidal, & Subramanian, 2016)
Untuk mengetahui kinerja dari AFE dan parameter-parameternya, dibentuk tabel relative error setiap data. Relative error dalam penelitian ini didefinisikan sebagai presentase selisih solusi yang diperoleh suatu kombinasi parameter terhadap solusi optimal data. Berikut ini diberikan hasil Rata-rata Relative Error Eksperimen AFE, untuk setiap parameter terhadap keseluruhan data permasalahan CVRP dalam bentuk tabel.
Tabel 2. Rata-rata Relative Error setiap parameter terhadap keseluruhan data
|
No |
Populasi |
Generasi |
Rata-rata Relative Error Jarak (%) |
Rata-rata Relative Error Kendaraan Minimal (%) |
|
1 |
50 |
200 |
85,4233 |
26 |
|
2 |
50 |
500 |
80,3193 |
30 |
|
3 |
50 |
750 |
69,5855 |
26 |
|
4 |
50 |
1250 |
79,6096 |
61 |
|
5 |
50 |
1500 |
82,5809 |
22 |
|
6 |
100 |
200 |
88,4239 |
30 |
|
7 |
100 |
500 |
80,7597 |
50 |
|
8 |
100 |
750 |
73,4759 |
42 |
|
9 |
100 |
1250 |
86,6391 |
86 |
|
10 |
100 |
1500 |
82,8790 |
50 |
|
11 |
150 |
200 |
86,7524 |
40 |
|
12 |
150 |
500 |
81,9767 |
56 |
|
13 |
150 |
750 |
87,3672 |
71 |
|
14 |
150 |
1250 |
76,7717 |
50 |
|
15 |
150 |
1500 |
80,5588 |
26 |
Sedangkan grafik yang menunjukkan hubungan antara setiap populasi dan generasi terhadap relative error diberikan sebagai berikut
|
XVV |
♦ Pop 50 |
|
Q RO 80 |
-5—u-4-_∣U∏ |
|
LlJ |
f ■ Pop |
|
60 | |
|
QJ |
100 |
|
t> (U 40 40 | |
|
OJ K | |
|
20 | |
|
n 0 | |
|
0 1000 2000 | |
|
Generasi | |
Gambar 5. Grafik hubungan antara populasi dan generasi terhadap rata-rata Relative Error Jarak
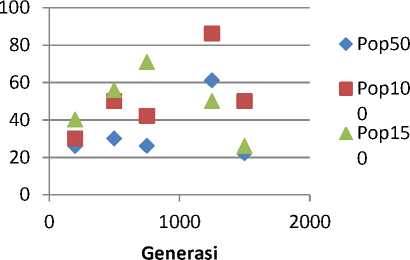
Gambar 6. Grafik hubungan antara populasi dan generasi terhadap rata-rata Relative Error Kendaraan Minimum
Secara umum, kinerja AFE dapat dilihat dari rata-rata relative error (̅̅̅̅) pada Tabel 2. ̅̅̅̅ jarak terkecil diperoleh oleh parameter populasi 50 dan generasi 750 yaitu sebesar 69,5855% dengan ̅̅̅̅ kendaraan minimumnya adalah sebesar 26%. Sedangkan ̅̅̅̅ kendaraan minimum terkecil diperoleh oleh parameter populasi 50 dan generasi 1500 yaitu sebesar 22% dengan ̅̅̅̅ jarak sebesar 82,5809%. Hal ini menunjukkan bahwa jarak tempuh yang kecil belum tentu menggunakan kendaraan yang lebih sedikit. Karena tujuan dari menyelesaikan CVRP adalah mencari jarak terpendek, maka parameter terbaik adalah populasi 50 dan generasi 1500.
Lebih lanjut, kedua grafik hubungan pada Gambar 5 dan Gambar 6, menunjukkan hasil yang diperoleh setiap populasi. Grafik pertama memperlihatkan hasil yang diperoleh setiap populasi dalam mencari jarak optimum. Ketiga populasi memperlihatkan hasil ̅̅̅̅ berada pada rentang nilai 70-90%. Untuk grafik kedua memperlihatkan hasil yang diperoleh setiap populasi dalam mencari kendaraan minimum. ^^^^^^^^^^^^^^^^^™ Ketiga populasi memiliki grafik dengan yang menyebar dengan peningkatan generasi tidak mempengaruhi hasil. Berdasarkan penjelasan tersebut, populasi terbaik AFE dalam menyeleasaikan kasus CVRP adalah populasi 50.
Hasil RE yang diperoleh AFE relatif besar. Hal ini dapat disebabkan oleh beberapa hal, yaitu:
-
1. AFE memecahkan masalah bukan dengan mencari solusi optimalnya, melainkan hanya menyeleksi kemungkinan solusi secara acak dan menyimpan solusi terbaik.
-
2. Tidak keseluruhan hasil kemungkinan solusi yang diperoleh dicek nilai fitnesnya. Ini diperlihatkan pada implementasi Algoritma ketika melakukan crossover. Ketika
melakukan crossover, tidak semua hasil dicari nilai fitneessnya. Sehingga ada kemungkinan solusi terbaik yang terlewatkan dalam proses crossover.
-
3. Domain dan fungsi keanggotaan dalam FIS yang digunakan dalam penelitian kurang tepat. Ini mengakibatkan hasil yang diperoleh parameter dalam pencarian solusi tidak maksimal.
-
4. KESIMPULAN DAN SARAN
KESIMPULAN
Berdasarkan hasil simulasi yang telah dilakukan terhadap 8 buah data menggunakan Algoritma Fuzzy Evolusi (AFE) dalam menyelesaikan CVRP, dapat disimpulkan Parameter terbaik dalam AFE berdasarkan hasil Relative Error nya adalah populasi 50 dan generasi 750 dengan nilai relative error jarak yaitu sebesar 69,5855% dan ̅̅̅̅ kendaraan minimum sebesar 26% dan populasi terbaiknya adalah populasi 50.
SARAN
Berdasarkan evaluasi yang dilakukan terhadap kinerja AFE, ada beberapa saran yang perlu dipertimbangkan dalam pengembangan tugas akhir ini, antara lain sebagai berikut: 1. Diharapkan adanya penelitian yang lebih mengkhusus tentang AFE, khususnya untuk model Xu yang meneliti aturan (Rule) dan batasan nilai untuk model mamdani yang digunakan.
-
2. Diharapkan adanya penelitian yang menggunakan model lain dari AFE selain model Xu.
-
3. Untuk permasalahan Vehicle Routing Problem (VRP), diharapkan adanya
penelitian lebih lanjut mengenai AFE yang dapat diterapkan dalam permasalahan VRP jenis lain selain CVRP.
DAFTAR PUSTAKA
Bjarnadóttir, Áslaug Sóley. 2004. Solving the Vehicle Routing Problem with Genetic Algorithms. Tesis. Technical University of Denmark.
Hartati, S., & Uyun, S. (2011). Computation of Diet Composition for Patients Suffering from Kidney and Urinary Tract Diseases with the Fuzzy Genetic System. International Journal of Computer Applications , 38-45.
Uchoa, E., Pecin, D., Pessoa, A., Poggi, M., Vidal, T., & Subramanian, A. (2016). New Benchmark Instances for the Capacitated Vehicle Routing Problem,. European Journal of Operational Research .
Xu, H. Y., & Vukovich, G. (1993). A Fuzzy Genetic Algorithm with Effective Search and Optimization. Proceedings of 1993 International Joint Conference on Neural Networks , 2967-2970.
Xu, H. Y., & Vukovich, G. (1994). Fuzzy Evolutionary Algorithms and Automatic Robot Trajectory Generation. Proceedings of the First IEEE International Conference on Evolutionary Computation , 595-600.
258
Discussion and feedback