PERAMALAN CURAH HUJAN MENGGUNAKAN METODE ANALISIS SPEKTRAL
on
E-Jurnal Matematika Vol. 5 (4), November 2016, pp. 183-193
ISSN: 2303-1751
PERAMALAN CURAH HUJAN MENGGUNAKAN METODE ANALISIS SPEKTRAL
Ni Putu Mirah Sri Wahyuni1§, I Wayan Sumarjaya2, I Gusti Ayu Made Srinadi3
-
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: mirahsriwahyuni@gmail.com]
-
2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
-
3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadiigustiayumade@yahoo.co.id] §Corresponding Author
ABSTRACT
The purpose of this research is the model of forecasting rainfall using spectral analysis method. To obtain complete information on characteristics of time series data we need to examine periodicity of the data. Examining the periodicity of time series data in the frequency domain is called spectral analysis. The results of spectral analysis show that periodogram is clearly dominated by a very large peak at frequency ω 10 = 0,083. This frequency corresponds to period of 12 cycle per month. Based on the results of analysis of time series data rainfall is SARIMA (0,1,1)(0,1,1)12 where the model can be written as X∗=X∗ .1 +X∗ -12 -X∗ -13 +a∗ - 0,9045a∗ .1 - 0,8199a∗ -12 + 0,7416a∗ -13 ․ The result indicates minimum rainfall happen in January and maximum rainfall happen in August.
Keywords: Forecasting, Periodicity, SARIMA, and Spectral Analysis.
Peramalan merupakan studi terhadap data historis untuk menemukan hubungan, kecenderungan, dan pola data yang sistematis (Makridakis, et al., 1999). Pada proses peramalan data yang digunakan adalah data deret waktu (time series). Deret waktu merupakan serangkaian pengamatan atau observasi terhadap peristiwa, kejadian atau variabel yang diukur dalam urutan waktu, misalnya jam, harian, bulanan, tahunan, dan lain-lain. Analisis data deret waktu memiliki tujuan yaitu untuk mengetahui perubahan data, kejadian atau variabel serta menemukan pola data sehingga berdasarkan pola data tersebut dapat diramalkan peristiwa yang akan terjadi di masa depan. Adapun contoh data deret waktu (time series) adalah data curah hujan. Hasil prediksi curah hujan yang akurat akan sedikit banyak memengaruhi aktivitas manusia. Misalnya dalam bidang pertanian, peramalan curah hujan digunakan untuk menentukan jenis tanaman yang ditanam dan menentukan awal musim tanam.
Ditinjau dari segi domain, analisis deret waktu dibagi menjadi dua yaitu analisis deret waktu pada domain waktu (time domain) dan analisis deret waktu pada domain frekuensi (frequency domain) (Chatfield, 1996). Analisis deret waktu dalam domain waktu yaitu berupa analisis yang menggunakan fungsi autokorelasi, autokorelasi parsial, dan autokovarians. Modelmodel deret waktu pada domain waktu antara lain Autoregressive (AR), Moving Average (MA), Autoregressive Moving Average (ARMA) dan Autoregressive Integrated Moving Average (ARIMA). Namun, analisis deret waktu pada domain frekuensi yaitu analisis deret waktu dianggap sebagai akibat dari adanya komponen siklus pada frekuensi berbeda yang sulit diperoleh dalam domain waktu.
Analisis spektral adalah penaksiran dalam domain frekuensi untuk menelaah periodisitas tersembunyi, yaitu periodisitas yang sulit ditemukan dalam domain waktu (Mulyana, 2004). Metode analisis spektral dapat dituliskan
dalam bentuk transformasi Fourier. Data yang digunakan dalam metode analisis spektral haruslah data yang stasioner. Untuk melihat periodisitas tersembunyi dari data deret waktu dapat dilihat dari periodogramnya.
Berdasarkan permasalahan tersebut, pada penelitian ini penulis ingin menunjukkan tentang aplikasi metode analisis spektral untuk mengetahui model peramalan dan aplikasi metode analisis spektral untuk meramalkan data deret waktu curah hujan.
Tujuan dari penelitian ini adalah untuk menentukan model dan memperoleh peramalan data deret waktu curah hujan menggunakan metode analisis spektral.
-
2. KAJIAN PUSTAKA
Stasioneritas Data
Menentukan model peramalan dengan metode analisis spektral menggunakan data deret waktu stasioner dalam mean dan varians. Pemeriksaan kestasioneran data dapat dilakukan dengan melihat plot data deret waktu. Ketidakstasioneran data dalam mean dapat diatasi dengan melakukan proses differencing agar data menjadi stasioner dengan notasi pada metode differencing adalah backward shift (B) sebagai berikut:
∇d=(1-B)d ․ (1)
Sedangkan untuk data yang tidak stasioner dalam varians dapat dilihat nilai λ (lamda) estimate pada transformasi Box-Cox. Transformasi varians secara umum menggunakan transformasi pangkat (power transformation) Box-Cox (Wei, 2006, p.85) sebagai berikut:
≠
T( %t)={ ^ , ≠0; (2)
ln(Xt ), λ=0․
Transformasi Box-Cox berdasarkan nilai A ditunjukkan pada Tabel 1.
Tabel 1. Transformasi Box Cox
|
λ |
Bentuk Transformasi |
|
-1 |
1 x~t |
|
-0,5 |
1 √ |
|
0 |
ln( Xt ) |
|
0,5 |
√ |
|
1 |
Xt |
Fungsi Autokovarians, Fungsi Autokorelasi (ACF) dan Fungsi Autokorelasi Parsial (PACF)
Fungsi autokovarians dan fungsi autokorelasi digunakan dalam analisis deret waktu sebagai pencocokkan model. Fungsi autokovarians dan autokorelasi yaitu (Wei, 2006, p.10):
Yk =(Xt -B)(Xt+k -B),
_ Cov ( xt,Xt+k) Yk
Pk =√Var ( Xt)√Var (xt+k)= ․
didefinisikan
(3)
(4)
Fungsi autokorelasi parsial digunakan untuk menunjukkan hubungan antara dan Xt+k dengan menganggap pengaruh semua kelambatan waktu yang lain adalah konstan. Fungsi autokorelasi parsial (PACF) didefinisikan sebagai berikut:
̂ - pk~ ∑ LA ̂ 'k-ι ,JPk-J
Φkk = ∑ ̂ -1 ,JPJ
(5)
dengan k j= k-1 j - kk Φk-1,k-J , untuk
j=1,2,…,k-1.
Analisis Spektral
Analisis spektral digunakan pada data deret waktu untuk mencari periodisitas tersembunyi. Analisis spektral atau juga disebut analisis spektrum diperkenalkan oleh Schuster yaitu seorang pekerja sosial pada abad ke-19 digunakan pada bidang kelautan, meterologi, dan astronomi dengan tujuan mencari periodisitas terembunyi (Bloomfield, 2000). Menentukkan spektrum dari data deret waktu stasioner adalah menggunakan transformasi
Fourier dari proses fungsi autokovarians (Nurhayati, et al., 2008). Transformasi Fourier Yk merupakan spektrum dari %t yaitu:
f(ω)=⅛ ∑k=-∞Yke lMk․ (6)
Persamaan (6) dapat diuraikan menggunakan hubungan Euler yaitu eιω =cosω+i sin ω dan e ιω =cosω-i sin ω maka diperoleh:
∞
f(ω)=1 ∑γke iωk
2 π Z—i k--∞
= + ⅛ {∑k=lYk cos(ωk)}․ (7)
Fungsi Pembangkit Autokovarians dan Fungsi Densitas Spektral
Misalkan Xt merupakan deret waktu stasioner bernilai real pada kovarians dan nilai tengah E( Xt)=E dan deret autokovarians ke-k adalah Yk dengan k=0,±1,±2,…, sehingga fungsi pembangkit autokovarians didefinisikan (Wei, 2006, p.274) sebagai berikut:
Y(B)=∑k=-∞YkBk = (B)Φ(B-1)․ (8)
Dengan demikian fungsi densitas spektral yaitu (Wegman, 1996):
f(ω)= π^ (e ιω )Φ(eιω)
2 2
= |φ( e--)| . (9)
Analisis Spektral Pada Model Deret Waktu Stasioner
-
1. Spektrum proses ARMA (P,q)
Model Autoregressive Moving Average (ARMA) merupakan suatu gabungan dari model AR( P ) dan MA( cI). Bentuk umum model ARMA (p,q) (Wei, 2006, p.274) yaitu:
%t = + Φ2Xt-2+⋯+ΦpXt-p + a-t +
Spektrum model ARMA ( P, cI ) dapat ditulis sebagai berikut:
-
2. Spektrum Proses White Noise
Model white noise (Wei, 2006, p.276)
Spektrum dari proses white noise dapat ditulis sebagai berikut:
2
-
3. Spektum Proses AR(1)
Bentuk umum model Autoregressive orde 1 atau AR (1) (Wei, 2006, p.276) dapat ditulis sebagai berikut:
Xt = + at ․
(13)
Spektrum pada proses AR (1) ditulis sebagai berikut:
f(ω)=
2π (l-2φ COS(ω) +φ2)․
(14)
-
4. Spektrum Proses MA(1)
Bentuk model proses Moving Average orde 1 atau MA(1) (Wei, 2006, p.277) adalah
sebagai berikut:
Xt = - θa^1. (15)
Adapun spektrum dari proses stasioner MA(1) adalah sebagai berikut:
/T2
f(ω)=⅛(1+θ2 -2θ cos(ω)) . (16)
-
5. Spektrum Model Musiman
Spektrum model musiman dengan musiman dua belas mempunyai model (Wei, 2006, p.279) sebagai berikut:
(1-ΦB12) Xt = . (17)
Jika model musiman stasioner maka spektrum dapat dihitung sebagai berikut:
f(ω)=
⅛______1______
2π (1-2Φ COS(12ω)+Φ2)․
(18)
Periodogram
Periodogram digunakan untuk melihat periodisitas tersembunyi dari data deret waktu. Penerapan analisis spektral dalam menetukkan model peramalan data deret waktu yaitu digunakan untuk melihat periodisitas dari data deret waktu dengan melihat plot periodogramnya. Periode yang diperoleh selanjutnya digunakan untuk menentukkan periode dari suatu model data deret waktu. Persamaan periodogram dituliskan sebagai berikut (Wei, 2006, p.290):
f nal. k - O
i⅛)-{i⅛+⅛). k—1.....M (19)
[ nah/2. k = j Jika n genaP
dengan Rp — √a2 + b2 amplitudo harmonik ke- k dan φp — arctan (— ^) fase harmonik ke- k.
Uji untuk Komponen Periodik Tersembunyi
Periode yang diperoleh dari plot periodogram selanjutnya akan diuji komponen periodik dari periodogram dapat dilakukan dengan menggunakan uji Fisher dengan statistik uji yaitu:
T — (20)
∑⅛√( ω fc)
dengan hipotesis sebagai berikut:
H0: periodogram tidak terdapat komponen periodik,
: periodogram terdapat komponen periodik.
Kriteria keputusan, apabila P (T > ga} — a. Jika nilai yang dihitung dari deret waktu lebih besar dari , maka ditolak yang berarti bahwa deret waktu berisi komponen periodik.
Proses Peramalan
-
1. Identifikasi Model
Menurut Wei (2006), langkah-langkah yang dilakukan dalam mengidentifikasi model adalah sebagai berikut:
-
a. Plot data deret waktu dan apabila data deret waktu tidak stasioner dalam varians maka dilakukan transformasi Box-Cox.
-
b. Menghitung dan memeriksa ACF dan PACF sampel dari deret asli dan bila data deret waktu diindikasikan tidak stasioner dalam rata-rata maka dilakukan proses differencing.
-
c. Menghitung dan memerika ACF dan PACF sampel dari data deret waktu hasil transformasi Box-Cox dan differencing untuk mengidentifikasi orde dari model ARIMA (p. d, q).
-
d. Menguji deterministik tren jika d > 0.
-
2. Estimasi Parameter
Uji signifikansi parameter bertujuan untuk mengetahui parameter tersebut layak digunakan dalam model. Uji signifikansi parameter menggunakan hipotesis sebagai berikut:
: — O (parameter tidak signifikan),
H1 :d ≠ 0 (parameter signifikan).
Statistik uji yang digunakan untuk
pengujian signifikansi parameter adalah statistik
uji t persamaannya adalah sebagai berikut:
SE ( S)
(21)
Apabila nilai |t| > t « atau p-value < a —
;n-p
0,05 maka dapat diputuskan menolak H0.
-
3. Diagnostik Model
Untuk menguji model yang telah ditetapkan sementara maka perlu dilakukan uji kesesuaian model untuk membuktikan bahwa model tersebut sudah sesuai digunakan untuk memodelkan data deret waktu dan melakukan peramalan. Dalam hal ini, pemeriksaan diagnostik model meliputi uji galat white noise dan uji kenormalan.
-
a. Uji White Noise
Untuk mengetahui autokorelasi antar galat sudah mengikuti proses white noise atau tidak maka perlu dilakukan pengujian galat white noise melalui nilai autokorelasinya dengan menggunakan uji kelayakan model Ljung Box, dengan hipotesis:
Hq : = =⋯ =0 (tidak terdapat
autokorelasi antar galat),
Hy : minimal ada satu Pk≠0 (terdapat autokorelasi antar galat).
Statistik uji Ljung Box (Wei, 2006, p.153) adalah
Q=(n+2)∑k=ι(n-k) ^1 ̂k ․ (22)
-
b. Uji Kenormalan
Uji ini dapat dilakukan dengan uji Shapiro Wilk dengan hipotesis:
Hq : galat berdistribusi normal, Hy : galat tidak berdistribusi normal.
Statistik uji Shapiro Wilk yaitu:
W= [∑i=ι ai (x∏-i+ι - Xi )] 2 ․ (23)
Kriteria pengambilan keputusan adalah jika
p-value < a = 0,05 maka tolak Hq , p-value ≥ a = 0,05 maka menerima Hq .
-
4. Pemilihan Model Terbaik
Tahap pemilihan model terbaik dilakukan dengan menggunakan kriteria Akaike’s Information Criterion (AIC) yang didefinisikan sebagai berikut:
AIC=n ln ̂ a +2m (24)
dengan n banyaknya pengamatan, ̂ a adalah estimasi likelihood maksimum dari σa , dan m adalah banyaknya parameter dalam model (Wei, 2006, p.156).
Data yang digunakan dalam penelitian ini adalah data curah hujan. Data curah hujan diambil dari stasiun Chicago West, Chicago Dupage Airport IL US pada situs (http://www.ncdc.noaa.gov/cdo.web/datasets) dari periode 2005-2015. Analisis data dalam penelitian ini menggunakan software R i386 3.3.1 dan MINITAB14. Langkah –langkah yang diambil dalam membuat prakiraan cuaca dengan metode analisis spektral:
-
1. Identifikasi data.
-
a. Melakukan plot data, digunakan untuk melihat apakah data deret waktu sudah stasioner atau belum.
-
b. Plot ACF dan PACF digunakan untuk mengidentifikasi model data deret waktu dan melihat kestasioneran data dalam mean.
-
c. Apabila data tidak stasioner dalam varians maka dilakukan transformasi Box-Cox.
-
d. Memeriksa apakah data telah stasioner
dalam mean dengan melakukan uji Augmented Dickey Fuller (ADF).
-
e. Apabila data tidak stasioner dalam mean
atau rata-rata maka dilakukan differencing untuk menstasionerkan data.
-
2. Setelah diperoleh data yang stasioner maka selanjutnya dilakukan analisis spektral untuk menentukan periode dari data deret waktu yang diperoleh dari periodogramnya.
-
3. Menguji komponen periodik tersembunyi dari periodogramnya.
-
4. Melakukan pendugaan model sementara melalui plot ACF dan PACF.
-
5. Tahap estimasi parameter model.
-
6. Melakukan pemeriksaan diagnostik model.
-
7. Pemilihan model terbaik dengan menggunakan kriteria AIC dengan pengambilan keputusan didasarkan pada nilai AIC minimum.
-
8. Membuat peramalan atau prakiraan curah hujan.
Langkah pertama yang dilakukan adalah melakukan plot data curah hujan dapat dilihat pada Gambar 1.
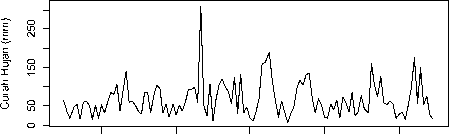
2006 2008 2010 2012 2014
Tahun
Gambar 1. Plot Data Deret Waktu Curah Hujan
menstasionerkan data dalam varians maka data
harus mengikuti nilai yang dihasilkan dari transformasi pertama yakni √ . Selanjutnya dibuat plot deret waktu untuk data curah hujan setelah dilakukan transformasi √ yang dapat dilihat dari Gambar 4 berikut ini.
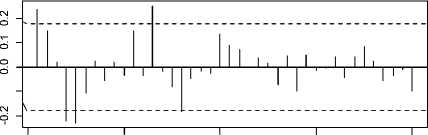
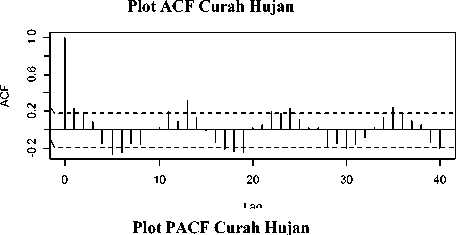
0 10 20 30 40
Lag
Gambar 2. Plot ACF dan PACF Curah Hujan
Pada Gambar 1 terlihat bahwa data curah hujan periode Januari 2005 sampai Desember 2014 berfluktuasi. Pola data seperti ini menunjukkan bahwa data curah hujan mempunyai pola musiman. Plot ACF dan PACF pada Gambar 2 menunjukkan bahwa laglag berpola sinusoidal yang mengindikasikan bahwa pada data curah hujan terdapat pengaruh musiman dan korelasi yang kuat pada data karena plot ACF dan PACF menujukkan lag-lag yang signifikan yaitu lag yang keluar dari batas selang kepercayaan. Lag-lag yang signifikan tersebut misalnya lag 1, 5 dan 6, sehingga perlu dilakukan differencing terhadap musiman. Kestasioneran data dalam varians akan diselidiki menggunakan plot transformasi BoxCox.
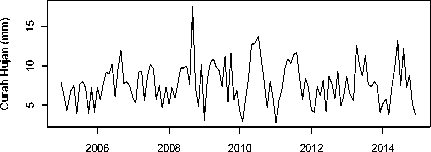
Tahun
Gambar 4. Plot Data Deret Waktu Curah Hujan Setelah Transformasi √
Melalui transformasi √ diperoleh bahwa data sudah stasioner dalam varians. Kemudian
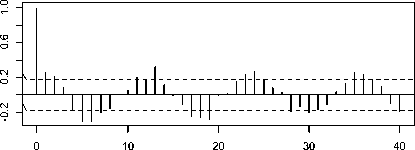
dilihat apakah data curah hujan sudah stasioner dalam rata-rata, dapat dilihat dari plot ACF dan PACF data hasil transformasi √ pada Gambar 5 berikut ini.
Plot ACF Hasil Transformasi √X~t
Lag
Box-Cox Plot of data
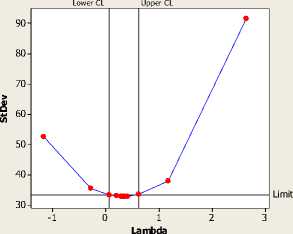
Lambda
(using 95.0% confidence)
Estimate 0.34
Lower CL 0.06
Upper CL 0.61
Rounded Value 0.50
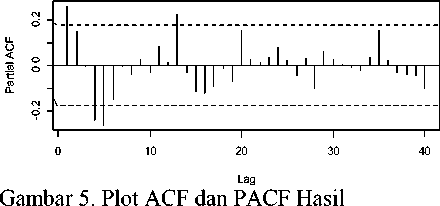
Plot PACF Hasil Transformasi √Xt
Transformasi √
Gambar 3. Plot Transformasi Box Cox
Berdasarkan Gambar 3 nilai Rounded Value ( )=0,5 yang menandakan bahwa data curah hujan belum stasioner dalam varians. Untuk
Plot ACF Gambar 5 di atas masih memperlihatkan bentuk autokorelasi sinusoidal hal ini memperkuat indikasi bahwa data tidak stasioner dalam rata-rata. Begitu pula pada
kasus musiman perlu dilakukan differencing karena turun secara lambat dengan bertambahnya lag. Pada plot PACF menunjukkan lag-lag yang signifikan yaitu pada lag 1, 3, 4, dan 12.
Mengingat bahwa data curah hujan sudah stasioner dalam varians maka selanjutnya dilakukan pengujian stasioner dalam rata-rata. Untuk melihat stasioner dalam rata-rata atau tidak maka dilakukan uji formal kestasioneran menggunakan uji ADF. Hipotesis yang digunakan adalah
H0: β — (d (data curah hujan tidak stasioner),
H1: β < 0 (data curah hujan stasioner).
Pengambilan keputusan yaitu apabila p-value < a maka tolak H0 dengan a — 0,05 merupakan tingkat kesalahan. Hasil analisis diperoleh p-value — 0,01 < 0,05 hal ini berarti cukup kuat untuk menerima . Jadi dapat disimpulkan bahwa data curah hujan sudah stasioner dalam rata-rata.
Plot ACF dan PACF hasil transformasi √X^t memperlihatkan adanya pengaruh musiman maka perlu dilakukan differencing terhadap tren dan musiman.
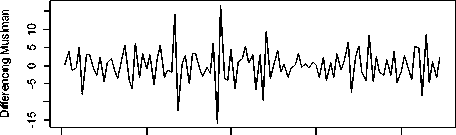
2006 2008 2010 2012 2014
Tahun
Gambar 6. Plot Deret Waktu Differencing Terhadap Tren dan Musiman
Pada Gambar 6 data curah hujan telah mengalami proses differencing tren dan musiman, grafik tidak lagi menunjukkan tren dan musiman dan bergerak di sekitar garis rata-rata. Dengan demikian, dapat disimpulkan bahwa data tersebut sudah stasioner dalam rata-rata dan varians. Lebih lanjut, dapat dilihat juga pada plot ACF dan PACF hasil differencing terhadap tren dan musiman.
Plot ACF Curah Hujan Hasil Differencing Tren dan Musiman
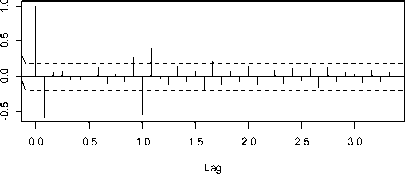
Plot PACF Curah Hujan Hasil Differencing Tren dan Musiman
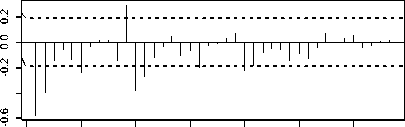
0.0 0.5 1.0 1.5 2.0 2.5 3.0
Lag
Gambar 7. Plot ACF dan PACF Hasil Differencing Tren dan Musiman
Setelah dilakukan differencing terhadap tren dan musiman ternyata plot ACF menurun secara cepat. Berdasarkan hasil plot ACF dan PACF pada Gambar 7 data sudah stasioner, namun masih ada lag yang keluar dari batas interval yaitu 2, 6, 11, 12, 13. Untuk memudahkan menentukkan orde dari musiman pada lag-lag yang signifikan pada plot ACF dan PACF maka tahap selanjutnya dilakukan pendekatan analisis spektral untuk membantu menentukan periode waktu curah hujan.
Analisis spektral merupakan analisis untuk mengetahui periodisitas tersembunyi dari data deret waktu. Periodogram yang dihasilkan dalam analisis spektral menunjukkan nilai amplitudo yang tertinggi. Hasil analisis spektral pada data curah hujan dari periodogramnya dapat dilihat pada Gambar 8 berikut ini.

0.1
0.2 0.3 0.4 0.5
Frequency
Gambar 8. Periodogram Data Curah Hujan
Pada periodogram menunjukkan bahwa puncak frekuensi tertinggi adalah pada
frekuensi ke-10 yaitu ω10 = 0,083. Pada frekuensi yang dihasilkan ini berhubungan dengan periode yaitu =12,048 atau dapat
<u10
dibulatkan menjadi 12 siklus per bulan. Hal ini menunjukkan bahwa karakteristik perubahan curah hujan cenderung akan mengalami kenaikan atau penurunan curah hujan setiap 12 bulan sekali.
Selanjutnya dilakukan uji Fisher untuk melihat signifikansi maksimum dari periodogram, sehingga diperoleh:
244 199
T = , = 0,299 dan , =0, 1132․
-
816, , , ,․
Karena nilai T = 0,299 > 0,1132 maka keputusan tolak Hq yaitu pada periodogram terdapat komponen periodik. Dengan demikian, dapat disimpulkan bahwa data curah hujan mengandung komponen periodik pada frekuensi 0,083 dan periode sebesar 12,048.
Setelah diperoleh periode dari data deret waktu maka hal ini menunjukkan bahwa data deret waktu curah hujan terdapat parameter musiman dengan periode 12. Langkah selanjutnya yaitu menentukkan model dari data deret waktu curah hujan.
Plot ACF dan PACF pada Gambar 7 terbentuk suatu dugaan sementara model SARIMA untuk data curah hujan. Model tersebut adalah SARIMA(1,1,2)(0,1,1)12,
SARIMA(1,1,2)(1,1,1)12, SARIMA(0,1,1)(0,1,1)12, SARIMA(0,1,1)(1,1,0)12, SARIMA(0,1,1)(1,1,1)12.
Estimasi parameter untuk model SARIMA(1,1,2)(0,1,1)12,
SARIMA(1,1,2)(1,1,1)12 ,SARIMA(0,1,1)(0,1,1 )12,SARIMA(0,1,1)(1,1,0)12, SARIMA(0,1,1)(1,1,1)12, adalah sebagai berikut:
Tabel 2. Estimasi Parameter model
SARIMA(1,1,2)(0,1,1)12
|
Parameter |
Estimasi |
p-value |
|
Φl |
-0,3515 |
0,008 |
|
̂ |
0,6490 |
0,000 |
|
̂ |
0,3565 |
0,003 |
|
Θ̂ |
0,8735 |
0,005 |
Tabel 3. Estimasi Parameter model
SARIMA(1,1,2)(1,1,1)12
|
Parameter |
Estimasi |
p-value |
|
Φl |
-0,2810 |
0,014 |
|
— ̂ |
0,7269 |
0,000 |
|
̂ |
0,2794 |
0,002 |
|
Φ̂ |
-0,2696 |
0,017 |
|
Θ̂ |
0,8624 |
0,000 |
Tabel 4. Estimasi Parameter model
SARIMA(0,1,1)(0,1,1)12
|
Parameter |
Estimasi |
p-value |
|
̂ |
0,9045 |
0,000 |
|
Θ̂ |
0,8199 |
0,000 |
Tabel 5. Estimasi Parameter model
SARIMA(0,1,1)(1,1,0)12
|
Parameter |
Estimasi |
p-value |
|
— ̂ |
0,9792 |
0,000 |
|
Φ |
-0,6278 |
0,000 |
Tabel 6. Estimasi Parameter model
SARIMA(0,1,1)(1,1,1)12
|
Parameter |
Estimasi |
p-value |
|
̂ |
0,9194 |
0,000 |
|
Φ̂ |
-0,2866 |
0,015 |
|
Θ̂ |
0,8124 |
0,000 |
Estimasi model pada Tabel 2 sampai Tabel 6 menunjukkan parameter dari setiap model signifikan pada tingkat kesalahan a = 0,05 sehingga kelima model tersebut dapat dijadikan sebagai pilihan. Selanjutnya dilakukan uji diagnostik untuk model yang nilai dugaan parameternya signifikan.
Model-model yang nilai dugaan parameternya signifikan selanjutnya akan dilakukan uji diagnostik untuk mengetahui apakah galat dari model sudah bersifat white noise dan berdistribusi normal. Untuk mengetahui galat bersifat white noise maka dilakukan uji Ljung Box.
Tabel 7. Uji Ljung Box
|
Model |
Lag | |||
|
12 |
24 |
36 |
48 | |
|
SARIMA(1,1,2)(0,1 ,1)12 |
0,10 6* |
0,36 7* |
0,36 6* |
0,50 9* |
|
SARIMA(1,1,2)(1,1 ,1)12 |
0,13 3* |
0,36 3* |
0,31 7* |
0,52 8* |
|
SARIMA(0,1,1)(0,1 ,1)12 |
0,22 5* |
0,48 4* |
0,57 2* |
0,72 3* |
|
SARIMA(0,1,1)(1,1 ,0)12 |
0,25 1* |
0,03 6* |
0,04 5* |
0,12 0* |
|
SARIMA(0,1,1)(1,1 ,1)12 |
0,33 6* |
0,57 0* |
0,58 8* |
0,78 1* |
Galat pada lag dari model dikatakan tidak berkorelasi apabila p-value untuk masing-masing galat pada setiap lag lebih besar dari tingkat kesalahan a = 0,05. Berdasarkan Tabel 7 terdapat empat model yang yang memenuhi asumsi galat white noise. Model tersebut adalah SARIMA(1,1,2)(0,1,1)12, SARIMA(1,1,2)(1,1,1)12, SARIMA(0,1,1)(0,1,1)12, SARIMA(0,1,1)(1,1,1)12.
Selanjutnya akan diuji kenormalan galat dari keempat model tersebut dengan menggunakan uji Shapiro Wilk dengan hipotesis yang digunakan adalah
H0: galat berdistribusi normal,
H1: galat tidak berdistribusi normal.
Pengambilan keputusan yaitu apabila p-value ≥ a maka terima H0 atau p-value < a maka tolak H0 dengan a = 0,05 merupakan tingkat kesalahan.
Tabel 8. Uji Kenormalan Shapiro Wilk
|
Model |
p-value |
|
SARIMA(1,1,2)(0,1,1)12 |
0,1986 |
|
SARIMA(1,1,2)(1,1,1)12 |
0,2986 |
|
SARIMA(0,1,1)(0,1,1)12 |
0,2248 |
|
SARIMA(0,1,1)(1,1,1)12 |
0,3060 |
Hasil uji Shapiro Wilk pada Tabel 8 menunjukkan bahwa p-value > a = 0,05 maka terima sehingga empat model tersebut
memenuhi asumsi galat berdistribusi normal.
Berdasarkan keempat kandidat model yang cocok dan telah memenuhi asumsi galat white
noise dan uji kenormalan galat maka selanjutnya akan dipilih model terbaik berdasarkan kriteria AIC. Nilai AIC pada keempat model dapat dilihat pada Tabel 9.
Tabel 9. Nilai AIC model SARIMA
|
Model |
AIC |
|
SARIMA(1,1,2)(0,1,1)12 |
522,79 |
|
SARIMA(1,1,2)(1,1,1)12 |
523,94 |
|
SARIMA(0,1,1)(0,1,1)12 |
519,14 |
|
SARIMA(0,1,1)(1,1,1)12 |
520,21 |
Pada Tabel 9 terlihat bahwa model SARIMA(0,1,1)(0,1,1)12 memiliki nilai AIC terkecil yaitu sebesar 519,14. Dengan demikian model peramalannya dapat dinyatakan sebagai berikut:
X t* = Xt*-1+Xt*-12-Xt*-13 + ^-0,9045αt-1 - 0,8199αt-12 + 0,7416α^.13
dengan X1 = √Xt dan at = √at.
Langkah selanjutnya yakni menentukan spektrum dari model SARIMA (0,1,1)(0,1,1)12. Spektrum dari model SARIMA (0,1,1)(0,1,1)12 dapat ditulis sebagai berikut:
^2
f(ω) = -^ [{1 + 0,8181 + 0,6722 + 0,5499 2^
-
—1,809 cos(ω) — 1,6398 cos(12ω) +1,4832 cos(11ω) — 1,3416 cos(12ω) + 1,4832 cos(13ω) — 1,2161 cos(ω)} /{4 — 4 cos(ω) + 2 cos(11ω) — 4 cos(12ω) +2 cos(13ω).
Spektrum dari model SARIMA (0,1,1)(0,1,1)12 dapat dilihat pada Gambar 9.
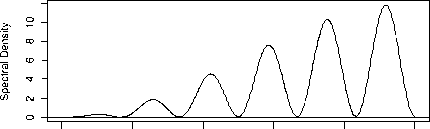
0.0 0.1 0.2 0.3 0.4 0.5
Frequency
Gambar 9. Spektrum Model SARIMA (0,1,1)(0,1,1)12
Gambar 9 menunjukkan bahwa terdapat lima buah puncak spektrum. Pada setiap puncak spektrum yang dihasilkan mengalami peningkatan setiap frekuensinya. Selain itu,
spektrum yang dihasilkan juga menunjukkan bagaimana kekuatan spektral didistribusikan sebagai fungsi-fungsi dari frekuensi. Spektrum pada data curah hujan adalah hubungan periode curah hujan dengan waktu terjadinya curah hujan.
Model SARIMA (0,1,1)(0,1,1)12 merupakan model terbaik sehingga perlu dilakukan peramalan untuk melihat apakah model tesebut sudah tepat atau tidak. Peramalan dilakukan untuk 12 periode ke depan dapat dilihat pada Tabel 10.
sebesar 0,083 pada frekuensi yang dihasilkan ini berkaitan dengan periode yaitu
=12,048 sehingga hal ini menunjukkan <u10
bahwa periode curah hujan terjadi setiap 12 bulan sekali.
-
2. Model terbaik dari data deret waktu untuk meramalkan data curah hujan yaitu model SARIMA (0,1,1)(0,1,1)12 secara matematis dapat ditulis sebagai berikut:
X∗=X∗ -1 +X∗ -12 -X∗ -13 +a∗
Tabel 10. Peramalan Curah Hujan Periode Januari 2015-Desember 2015
+0,7416a∗
|
Periode |
Peramalan |
Aktual |
|
Januari 2015 |
29,28 |
20,83 |
|
Februari 2015 |
32,05 |
3,81 |
|
Maret 2015 |
44,10 |
12,7 |
|
April 2015 |
76,53 |
107,7 |
|
Mei 2015 |
85,63 |
112,5 |
|
Juni 2015 |
81,56 |
203,5 |
|
Juli 2015 |
86,29 |
82,8 |
|
Agustus 2015 |
90,53 |
80,26 |
|
September 2015 |
70,16 |
112 |
|
Oktober 2015 |
53,93 |
51,31 |
|
Nopember 2015 |
40,22 |
85,6 |
|
Desember 2015 |
38,93 |
129,8 |
Tabel 10 menunjukkan hasil peramalan bahwa curah hujan minimum terjadi pada bulan Januari sedangkan curah hujan maksimum terjadi pada bulan Agustus. Plot peramalan curah hujan dapat dilihat pada Gambar 10.
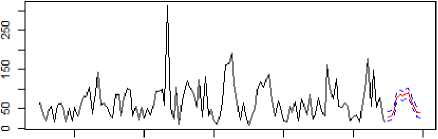
2006 2008 2010 2012 2014 2016
Time
Gambar 10 Plot Peramalan Curah Hujan
Berdasarkan hasil dan pembahasan pada penelitian ini diambil kesimpulan yaitu:
1. Analisis spektral dapat digunakan untuk melihat keperiodikan data curah hujan dengan mencari periodogramnya. Hasil analisis diperoleh frekuensi curah hujan
dengan X∗=√Xf dan a∗=√at .
3. Hasil peramalan menggunakan model SARIMA (0,1,1)(0,1,1)12 memperlihatkan bahwa curah hujan minimum terjadi pada bulan Januari sedangkan curah hujan maksimum terjadi pada bulan Agustus.
Pada penelitian ini pengaruh pencilan pada data curah hujan belum dipertimbangkan dalam menentukan model peramalan. Oleh karena itu, saran yang dapat dipertimbangkan dalam penelitian selanjutnya adalah melakukan deteksi terhadap pencilan sehingga diharapkan dapat meningkatkan keakuratan hasil peramalan.
DAFTAR PUSTAKA
Bloomfield, P. 2000. Fourier Analysis of Time Series. Second Edition. A Wiley
Interscience Publication. New York.
Chatfield, C. 1996, The Analysis of Time Series: An Introduction, Fifth Edition, Chapman and Hall, New York. http://gen.lib.rus.ec. Diakses 11 Maret 2016.
Makridakis, S., Wheelwright, S. C., &
McGee,V.E. 1999. Metode dan Aplikasi Peramalan. Jakarta: Erlangga.
Mulyana. 2004. Analisis Data Deret Waktu. Fakultas Matematika dan Ilmu Pengetahuan Alam UNPAD: Bandung.,
http://id.scribd.com/doc/19005304/Analisis -Data-Deret-Waktu. Diakses 30 Mei 2016.
Nurhayati, N., Pasaribu, U. S., Hakim, D. M., & Neswan, O. 2008. Spektrum Gstar(1;1). Jurnal Matematika dan Sains, vol.13 No.4 , pp. 118-124. http://journal.itb.ac.id/jms /article/view/206. Diakses 24 Januari 2016.
Wegman, E. J. 1996. Time Series Analysis: Theory, Data Analysis and Computation. George Mason University.
Wei, W.W.S. 2006. Time Series Analysis: Univariate and Multivariate Methods. Addison-Wesley Publishing Company. New York. http://gen.lib.rus.ec. Diakses 11 Maret 2016
193
Discussion and feedback