PENERAPAN METODE FUZZY SUGENO UNTUK MENENTUKAN HARGA JUAL SEPEDA MOTOR BEKAS
on
E-Jurnal Matematika Vol. 5 (4), November 2016, pp. 176-182
ISSN: 2303-1751
PENERAPAN METODE FUZZY SUGENO UNTUK MENENTUKAN HARGA JUAL SEPEDA MOTOR BEKAS
Ami Hilda Agustin1§, G.K. Gandhiadi2, Tjokorda Bagus Oka3
1Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: amihilda.a@gmail.com] 2Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: gandhiadigk@yahoo.com] 3Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: tjokordabagusoka@gmail.com] §Corresponding Author
ABSTRACT
Fuzzy logic is a way to map an input space into an output space. The basic of fuzzy logic is fuzzy set theory. In the fuzzy set theory, the role of membership degree is important to determine the presence of elements in a set. Membership degree is the fundamental feature of reasoning in fuzzy logic. There are several methods that are often used in solving fuzzy inference system, one of them is fuzzy Sugeno method. The aim of this research is applications of fuzzy methods is to forecast to determine the selling price of used motorcycles. In determining the selling price of used motorcycles, there are several things that need to be considered, namely : the production year of the motorcycles, the physical condition of the motorcycles, the origin of the license plates, and the purchase price of the motorcycles. The calculation can be done by using Matlab program. The result obtained were then tested using the Mean Absolute Percentage Error (MAPE) by calculating difference between the selling price of dealer minus the selling price of fuzzy Sugeno then divided by the selling price of dealer. From the test result, MAPE value obtained was 5,64% . This indicates that error rate below 10%, so we can say the result of these calculation is considerably accurate.
Keywords: Fuzzy Sugeno Method, Matlab, MAPE, Used Motorcycle
Sistem transportasi memiliki peranan yang sangat penting dalam kehidupan sehari-hari. Mobilitas penduduk maupun barang akan terselenggara dengan menggunakan alat transportasi. Jumlah kendaraan bermotor cenderung meningkat dari tahun ke tahun. Salah satu alat transportasi yang paling banyak digunakan adalah kendaraan bermotor yakni jenis sepeda motor. (BPS, 2013:1). Sepeda motor merupakan kendaraan yang paling banyak menjadi pilihan masyarakat. Selain praktis, harga sepeda motor juga relatif terjangkau. Sepeda motor juga bisa menjadi solusi untuk menghindari kemacetan yang sering terjadi di jalan raya (Triyatno,2014).
Menurut Andini dan Rahardjo (2012), harga merupakan faktor yang berpengaruh secara signifikan terhadap keputusan pembelian oleh konsumen dalam transaksi jual beli. Dengan
demikian, penentuan harga jual sepeda motor bekas menjadi suatu pertimbangan oleh pemilik dealer. Dari hasil wawancara terhadap salah satu dealer di Jimbaran yakni pemilik dealer Sodik Motor, dalam penentuan harga jual sepeda motor bekas, ada beberapa hal yang mempengaruhinya. Adapun beberapa hal yang mempengaruhi tersebut yaitu tahun pembuatan motor yang tertera pada BPKB dan STNK, kondisi fisik motor, plat nomor motor, serta harga beli motor.
Pada penelitian sebelumnya, berkaitan dengan penentuan harga jual sepeda motor bekas telah dilakukan oleh Prasetya dan Rahayu (2015), yang menggunakan metode tsukamoto untuk menentukan harga jual sepeda motor bekas. Selanjutnya, Sunoto dan Lukman (2015), juga telah melakukan penelitian tentang penentuan harga jual sepeda motor bekas menggunakan metode mamdani. Kemudian,
Istraniady dkk (2013), melakukan perbandingan antara metode tsukamoto dan mamdani dalam menentukan harga jual sepeda motor bekas. Sementara itu, sejauh ini peneliti belum menemukan penelitian mengenai penentuan harga jual sepeda motor bekas menggunakan metode Sugeno. Oleh karena itu dalam penelitian ini dibahas penerapan metode fuzzy Sugeno untuk menentukan harga jual sepeda motor bekas.
Penelitian ini dilakukan untuk mengetahui bagaimana menentukan harga jual sepeda motor bekas dengan menggunakan metode fuzzy Sugeno.
Logika fuzzy merupakan salah satu komponen pembentuk soft computing. Dasar logika fuzzy adalah teori himpunan fuzzy. Logika fuzzy merupakan suatu cara yang tepat untuk memetakan suatu ruang input ke dalam suatu ruang output (Kusumadewi dan Purnomo, 2010:1).
Himpunan adalah kumpulan atau koleksi objek-objek yang mempunyai kesamaan sifat tertentu (Salikin, 2011). Himpunan fuzzy merupakan suatu pengembangan lebih lanjut tentang konsep himpunan dalam matematika. Pada himpunan tegas (crisp), nilai keanggotaan dalam suatu himpunan A(μA(x)) memiliki dua kemungkinan, yaitu :
-
a) Satu (1) yang berarti bahwa suatu item menjadi anggota dalam suatu himpunan, atau
-
b) Nol (0) yang berarti bahwa suatu item tidak menjadi anggota dalam suatu himpunan.
Jika X adalah koleksi dari objek-objek yang secara umum dilambangkan oleh x, maka suatu himpunan fuzzy A dalam X didefinisikan himpunan pasangan berurutan:
A = {(x,μ A(×S)∖x∈X}, (1)
dengan μA (x) adalah fungsi keanggotaan untuk himpunan fuzzy A . Fungsi keanggotaan memetakan setiap elemen dari X ke derajat
keanggotaan yang terletak pada rentang [0,1] (Jang dkk, 1997). Himpunan fuzzy memiliki 2 atribut (Kusumadewi dan Purnomo, 2010:6), yaitu: linguistic dan numeris.
Definisi fungsi keanggotaan (membership function) menurut Kusumadewi dan Purnomo (2010:8), adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaan yang memiliki interval antara 0 sampai 1. Fungsi-fungsi keanggotaan antara lain representasi diskrit, representasi kurva segitiga, dan representasi kurva trapesium.
-
1. Operator AND
Operator AND (intersection) berhubungan dengan operasi irisan (∩) pada himpunan.
μA ∩b =μA(χ)∩μβ(y)
= min(μA a(x), μβ(y)) (2)
Misalkan himpunan fuzzy C adalah irisan dari himpunan fuzzy A dan himpunan fuzzy B , sehingga dapat didefinisikan sebagai berikut : C = (A∩B)(x)
= m m{A)x),B)x)}
= A(x) ∩ B(x~),Xx ∈ X
dengan derajat keanggotaannya adalah : μ c (x) = m i n(βA(×μ Bb(x))
= (μ a(x),Bb(x)),∀x ∈ X
-
2. Operator OR
Operator OR (Union) berhubungan dengan operasi gabungan pada himpunan.
Ba ∪b = BaM uμlf∖A
= mxx(βA(x), Bety)) (3)
Misalkan himpunan fuzzy C adalah gabungan dari himpunan fuzzy A dan himpunan fuzzy B, sehingga dapat didefinisikan sebagai berikut : C = (A∪B)(x)
= max{A)x),B)x)}
= A(x) U B(x),Vx ∈ X
dengan derajat keanggotaannya adalah : μ c (x) = max{μ A(X)iBb(XS)
= (μ A(x),BB(x)),∀x ∈ X
-
3. Operasi NOT
Operator NOT berhubungan dengan operasi komplemen pada himpunan.
Ac=1-A(x)
Dengan derajat keanggotannya adalah
Va' =1-Va (x) (4)
-
2.5 Metode Fuzzy Inference System (FIS)
Sugeno
Salah satu metode FIS yang dapat digunakan untuk pengambilan keputusan adalah metode Sugeno. Untuk memperoleh output dari metode fuzzy Sugeno diperlukan 4 tahap, yaitu :
-
1. Pembentukan himpunan fuzzy (fuzzifikasi)
-
2. Aplikasi fungsi implikasi
Aturan dasar fuzzy mendefinisikan hubungan antara fungsi keanggotaan dan bentuk fungsi keanggotaan hasil. Pada metode Sugeno, output (konsekuen) sistem tidak berupa himpunan fuzzy melainkan berupa konstanta atau persamaan linier. Menurut Kusumadewi dan Purnomo (2010:46) metode Sugeno terdiri dari 2 jenis , yaitu :
-
a) Model Fuzzy Sugeno Orde-Nol
Bentuk umum dari model fuzzy Sugeno Orde-Nol adalah
IF (x1is A1)ο (X2IsA2)ο…ο (Xftis Aft)
THEN z = (5)
dengan A^ adalah himpunan fuzzy ke-i sebagai anteseden, dan k adalah suatu konstanta (tegas) sebagai konsekuen.
-
b) Model Fuzzy Sugeno Orde-Satu
Bentuk umum dari model fuzzy Sugeno Orde-Satu adalah
IF (x1is A1)ο (x2isA2)ο…ο (Xftis Aft)
THEN z = ∗ X1+⋯+Pn ∗ xN
+Q (6)
dengan Ai adalah himpunan fuzzy ke-i sebagai anteseden, dan Pi adalah suatu konstanta (tegas) ke-i dan q juga merupakan konstanta pada konsekuen
-
3. Komponen aturan (agregasi)
Apabila sistem terdiri dari beberapa aturan, maka inferensi diperoleh dari kumpulan dan korelasi antar aturan yaitu menghitung hasil dari ∑7" = 1 CtyZy dengan R adalah banyaknya aturan (rule), Cty adalah α predikat ke-r, dan Zy adalah output pada anteseden aturan ke-r.
-
4. Penegasan (defuzzifikasi)
Defuzzifikasi pada metode Sugeno dilakukan dengan cara mencari nilai rata-ratanya.
∑1I=I UjZj ∑i~ι ai
(7)
dengan at adalah α predikat ke-i, dan zi adalah output pada anteseden aturan ke-i.
-
2.6 Mean Absolute Percentage Error (MAPE)
Mean Absolute Percentage Error (MAPE) merupakan suatu ukuran akurasi peramalan dari suatu metode peramalan. Caranya yaitu dengan menghitung selisih dari output yang diperoleh dengan data sebenarnya, kemudian dibagi dengan data sebenarnya. Hasilnya yang berbentuk persentase kemudian dimutlakkan.
Perhitungan ini dilakukan pada setiap amatannya, kemudian dirata-ratakan.
Hasil peramalan sangat bagus jika nilai MAPE kurang dari 10% sedangkan nilai MAPE dikatakan bagus jika kurang dari 20% (Harun,1999). MAPE didefinisikan
sebagai berikut :
∑I| χi-Fi |
MAPE = -Zl x 100% (8)
n
dengan : Xi = nilai data asli amatan ke
i
Fi = nilai ramalan amatan ke- i n = banyaknya data
Pada penelitian ini data yang digunakan adalah data primer dan sekunder yang yang diperoleh dari dealer Sodik Motor sampai akhir bulan maret 2016. Variabel input yang digunakan pada penelitian ini terdiri atas tahun motor, kondisi fisik motor, plat nomor motor dan harga beli motor.
Pada penelitian ini menggunakan metode Sugeno orde-satu. Adapun langkah yang dilakukan adalah sebagai berikut :
-
1. Menentukan range dan fungsi keanggotaan dari masing-masing atribut linguistik,
-
2. Penentuan fungsi pada konsekuen untuk masing-masing aturan implikasi,
-
3. Membentuk aturan implikasi fuzzy dengan mengkombinasikan setiap atribut linguistik pada setiap variabel input,
-
4. Melakukan defuzzifikasi dengan
menghitung rata-rata terbobot dari semua aturan implikasi fuzzy,
-
5. Melakukan simulasi Fuzzy Inference System Sugeno orde-satu untuk menentukan ketepatan harga jual sepeda motor bekas.
-
6. Menghitung nilai MAPE untuk menentukan keakuratan dari Fuzzy Inference System yang digunakan.
Untuk memudahkan perhitungan, dalam penelitian ini digunakan program Matlab R2009a.
b) Kondisi Fisik
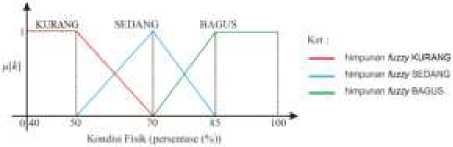
Gambar 2. Fungsi Keanggotaan Kondisi Fisik
Pada variabel kondisi fisik (dinotasikan sebagai k) akan dibagi menjadi 3 himpunan fuzzy, yaitu JELEK, SEDANG, dan BAGUS. Himpunan fuzzy direpresentasikan dengan fungsi keanggotaan sebagai berikut :
Hjelek [k]={70-50
0
, 40≤k≤50
, 50<k<70
,k≥70
(12)
4. HASIL DAN PEMBAHASAN
0
I ⅛-50 Hsedang [k]=\ 70-50 j 85-fe 85-70
,k≤50atau k≥85
, 50<k≤70
, 70<k<85
(13)
Hbagus [k]={85-70
a) Tahun Motor
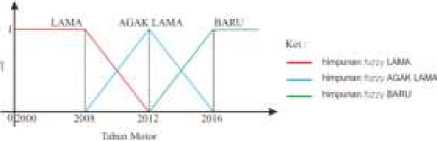
Gambar 1. Fungsi Keanggotaan Tahun Motor
,k≤70
, 70<k<85
,k≥85
Pada variabel tahun motor (dinotasikan sebagai t) akan dibagi menjadi 3 himpunan fuzzy, yaitu LAMA, AGAK LAMA, dan BARU. Himpunan fuzzy direpresentasikan dengan fungsi keanggotaan sebagai berikut :
(14)
c) Plat Nomor
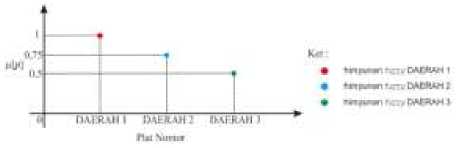
Gambar 3. Fungsi Keanggotaan Plat Nomor
I1LAMA [t]={
1 ,2000≤t ≤ 2008
, 2008<t < 2012
2012-2008
0 ,t ≥ 2012
(9)
0
I t-2008
Hagak lama [t]=\ 2012-2008
I 2016-t
V 2016-2012
,t ≤ 2008 CltClU t ≥ 2016 , 2008<t ≤ 2012
,2012<t < 2016 (10)
Hbaru [t]={
0 ,t ≤ 2012
, 2012 < t < 2016 2016-2012
1 ,t ≥ 2016
Pada variabel plat nomor (dinotasikan sebagai P) akan dibagi menjadi 3 himpunan fuzzy, yaitu DAERAH 1, DAERAH 2, dan DAERAH 3. DAERAH 1 mencakup kabupaten Badung dan Kota Denpasar. DAERAH 2 mencakup kabupaten Gianyar, Tabanan, dan Bangli. DAERAH 3 mencakup Kabupaten Jembrana, Buleleng, Klungkung, dan Karangasem. Himpunan fuzzy DAERAH 1, DAERAH 2 dan DAERAH 3 direpresentasikan dengan fungsi keanggotaan diskrit sebagai berikut :
(11)
1 ,P∈ DAERAH 1
Hdaerah i [P]={0 , P∈ lainnya (15)
0,75 , P∈ DAERAH 2
Rdaerah2 [P]={0 , P∈ lainnya (16)
0,5 , P∈ DAERAH 3
Rdaerah3 [P]={0 , P∈ lainnya (17)
Untuk input pada program Matlab, elemen dari DAERAH 1 dinotasikan 1, elemen dari DAERAH 2 dinotasikan 2, dan elemen dari DAERAH 3 dinotasikan 3.
ini, anteseden direpresentasikan dengan proposisi dalam himpunan fuzzy, sedangkan konsekuen direpresentasikan dengan sebuah persamaan linier. Konsekuen pada penelitian ini mengacu pada data yang diperoleh di lapangan ditambah dengan keterangan dari narasumber. Sehingga diperoleh rumus persamaan linear pada konsekuen adalah
d) Harga Beli
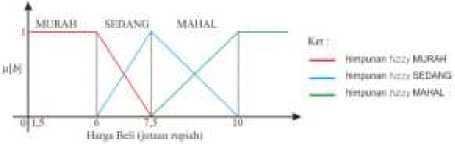
Gambar 4. Fungsi Keanggotaan Harga Beli
Pada variabel harga beli (dinotasikan sebagai b) akan dibagi menjadi 3 himpunan fuzzy, yaitu MURAH, SEDANG, dan MAHAL. Himpunan fuzzy direpresentasikan dengan fungsi keanggotaan sebagai berikut :
Rjelek [b]=
1 , 1.500.000 ≤ b ≤ 6.000.000
{
7.500.000-b
7.500.000-6.000.000
6.000.000 < b < 7.500.000
Harga Jual = + Konstanta (20)
Nilai konstanta merupakan besarnya keuntungan dan besarnya biaya perbaikan. Nilai konstanta diperoleh dari besarnya keuntungan dan besarnya biaya perbaikan dengan cara memperhatikan derajat keanggotaan tertinggi dari masing-masing himpunan pada data yang diperoleh.
4.3 Defuzzifikasi
Defuzzifikasi dibuat sesuai persamaan (7) dengan aturan implikasi sebanyak 81. diperoleh α dan z sebanyak 81 yang mewakili secara berturut-turut α predikat dan output untuk setiap aturan. Berdasarkan α predikat dan output disetiap aturan, maka defuzzifikasi dapat diperoleh sebagai berikut :
0 , b ≥ 7.500.000
(18)
Rsedang [b]=
∑fJ1 UiZi =∑ ^1ai
(21)
0 ,b ≤ 6.000.000 atau b ≥ 10.000.000
{
b-6.000.000
7.500.000-6.000.000
6.000.000 < b ≤ 7.500.000
10.000.000-b
10.000.000-7.500.000
7.500.000 < b < 10.000.000
(19)
Rbagus[b]=
{
0
b-7.500.000
10.000.000-7.500.000
1
b ≤ 7.500.000
7.500.000 < b < 10.000.000
b ≥ 10.000.000 (20)
dengan : at = predikat pada aturan ke- i zi = pada aturan ke-i
4.4 Simulasi Fuzzy Inference System Sugeno
Orde-Satu
4.2 Pembentukan Aturan Implikasi Fuzzy
Pembentukan aturan implikasi fuzzy diperoleh dengan mengkombinasikan setiap atribut linguistik pada masing-masing variabel input. Dari keempat variabel input, masing-masing memiliki 3 atribut linguistik. Sehingga aturan implikasi yang dapat dibentuk yakni 34 =81 aturan implikasi fuzzy. Metode inferensi fuzzy yang akan digunakan adalah Metode Fuzzy Sugeno orde-satu. Pada metode
Untuk simulasi perhitungan fuzzy digunakan program Matlab. Urutan proses pembuatan program yaitu :
-
1. memasukkan range dan fungsi keanggotaan untuk masing-masing variabel input,
-
2. memasukkan nilai konstanta pada konsekuen untuk variabel output harga jual,
-
3. menyusun aturan implikasi fuzzy pada mesin inferensi,
-
4. Untuk menghitung harga jual, dapat dilakukan dengan cara memasukkan data
pada kolom input secara berurutan, yakni dengan spasi. Contoh : [2010 85 1
data tahun motor, kondisi fisik motor, plat 5500000]
nomor motor, dan harga beli motor. Dari keseluruhan amatan, diperoleh hasil
Penulisan input diawali dan diakhiri simulasi sebagai berikut :
dengan kurung siku ([ ]) dan dipisahkan
Tabel 1. Data dan Hasil Simulasi
|
No |
Tipe Motor |
Tahun Motor |
Kondisi Fisik |
Plat Nomor |
Harga Beli |
Harga Jual Dealer (X) |
Harga Jual Sugeno (F) |
Selisih (X-F) |
|
1 |
Mio Sporty |
2010 |
85 |
Badung |
5.500.000 |
7.000.000 |
7.000.000 |
0 |
|
2 |
Jupiter MX CW |
2009 |
90 |
Badung |
7.500.000 |
8.500.000 |
8.860.000 |
-360.000 |
|
3 |
Mio CW |
2011 |
80 |
Denpasar |
6.800.000 |
7.500.000 |
8.350.000 |
-850.000 |
|
4 |
Mio Soul |
2010 |
85 |
Badung |
6.200.000 |
7.500.000 |
7.750.000 |
-250.000 |
|
5 |
Scoopy FI Sporty |
2015 |
90 |
Badung |
13.000.000 |
14.000.000 |
14.300.000 |
-300.000 |
|
6 |
Vario CW |
2011 |
80 |
Badung |
9.200.000 |
10.000.000 |
10.500.000 |
-500.000 |
|
7 |
Vario CW |
2010 |
75 |
Tabanan |
7.750.000 |
9.000.000 |
8.830.000 |
170.000 |
|
8 |
Xeon |
2011 |
70 |
Gianyar |
7.500.000 |
8.500.000 |
8.500.000 |
0 |
|
9 |
Vega ZR |
2009 |
75 |
Badung |
4.600.000 |
6.500.000 |
5.960.000 |
540.000 |
|
10 |
Vario Techno CW |
2011 |
80 |
Buleleng |
11.500.000 |
10.000.000 |
12.800.000 |
-2.800.000 |
|
11 |
Jupiter MX CW |
2010 |
85 |
Badung |
8.500.000 |
9.000.000 |
10.100.000 |
-1.100.000 |
|
12 |
Blade |
2009 |
60 |
Badung |
5.000.000 |
6.000.000 |
6.160.000 |
-160.000 |
|
13 |
Vario Techno 125 |
2013 |
90 |
Denpasar |
11.500.000 |
13.000.000 |
12.900.000 |
100.000 |
|
14 |
Beat FI ISS |
2015 |
95 |
Badung |
10.000.000 |
11.500.000 |
11.300.000 |
200.000 |
|
15 |
Satria FU 150 |
2012 |
95 |
Denpasar |
11.100.000 |
12.500.000 |
12.500.000 |
0 |
|
16 |
Vario CW |
2009 |
80 |
Badung |
7.000.000 |
8.500.000 |
8.340.000 |
160.000 |
|
17 |
Beat FI |
2014 |
90 |
Badung |
10.000.000 |
11.500.000 |
11.300.000 |
200.000 |
|
18 |
Mio Soul |
2011 |
85 |
Badung |
6.000.000 |
7.500.000 |
7.500.000 |
0 |
|
19 |
Spacy |
2012 |
90 |
Badung |
6.500.000 |
8.500.000 |
8.330.000 |
170.000 |
|
20 |
Shogun 110 |
2002 |
65 |
Badung |
2.500.000 |
3.500.000 |
3.500.000 |
0 |
|
21 |
Beat FI |
2013 |
90 |
Badung |
9.200.000 |
11.000.000 |
10.800.000 |
200.000 |
|
22 |
Mio Sporty |
2010 |
85 |
Badung |
5.500.000 |
7.000.000 |
7.000.000 |
0 |
|
23 |
Vario CW |
2014 |
95 |
Badung |
11.000.000 |
12.500.000 |
12.300.000 |
200.000 |
|
24 |
Vixion |
2013 |
90 |
Badung |
11.000.000 |
13.000.000 |
12.400.000 |
600.000 |
|
25 |
Mio Sporty |
2010 |
80 |
Badung |
9.000.000 |
7.500.000 |
10.300.000 |
-2.800.000 |
|
26 |
Mio Soul |
2010 |
80 |
Badung |
5.500.000 |
7.500.000 |
7.000.000 |
500.000 |
|
27 |
Mio Soul |
2011 |
80 |
Badung |
6.000.000 |
8.000.000 |
7.530.000 |
470.000 |
|
28 |
Mio Soul |
2011 |
85 |
Denpasar |
6.500.000 |
8.000.000 |
8.140.000 |
-140.000 |
|
29 |
Xeon |
2010 |
75 |
Badung |
8.000.000 |
8.000.000 |
9.230.000 |
-1.230.000 |
|
30 |
Jupiter MX New |
2011 |
90 |
Badung |
7.500.000 |
10.000.000 |
9.620.000 |
380.000 |
|
31 |
Supra X 125 |
2009 |
80 |
Badung |
6.750.000 |
9.000.000 |
8.120.000 |
880.000 |
|
32 |
Blade |
2009 |
75 |
Badung |
6.500.000 |
7.500.000 |
7.840.000 |
-340.000 |
-
3.5 Perhitungan Keakuratan Hasil
Berdasarkan tabel 1, diperoleh nilai MAPE sebagai berikut :
|. -^-l∖7.OOO.000
/
(-360 .000)
I o enn nnn ∕ + ⋯
..
32
(-340 .000) ∖7.500.000
/|
x 100%
1,804048101
32
x 100%
∑ ?=i∣ ×l~Fl |
MAPE= ∑| .Ji | x 100%
= 5,6376503%
|. Xi /+( X2 /+ → .
32
'x32~f32/|
■ X32 /| x 100%
Diperoleh nilai MAPE sebesar 5,6376503% atau 5,64%. Karena nilai yang diperoleh kurang dari 10% berarti hasil yang diperoleh dari simulasi sangat bagus.
Berdasarkan pembahasan mengenai Penerapan Metode Fuzzy Sugeno untuk Menentukan Harga Jual Sepeda Motor Bekas, maka dapat disimpulkan bahwa metode fuzzy Sugeno dapat diterapkan dalam menentukan harga jual sepeda motor bekas dengan variabel-variabel input, yaitu : tahun motor, kondisi fisik motor, plat nomor, dan harga beli motor. Perhitungan hasil dilakukan dengan menggunakan program Matlab R2009a, kemudian dilakukan pengujian untuk mengetahui keakuratan dari hasil yang diperoleh dengan menggunakan metode Mean Absolute Percentage Error (MAPE). Nilai MAPE yang diperoleh sebesar 5,64%. Hal ini menunjukkan bahwa tingkat kesalahan dibawah 10%, sehingga dapat dikatakan hasil perhitungan tersebut sangat bagus. Dengan demikian, hasil dari perhitungan ini dapat digunakan oleh pemilik dealer sebagai alat bantu dalam menentukan harga jual sepeda motor bekas.
4.2 Saran
Permasalahan yang diambil pada Penerapan Metode Fuzzy Sugeno untuk Menentukan Harga Jual Sepeda Motor Bekas ini masih sangat sederhana. Masih terdapat cara yang dapat digunakan untuk menentukan harga jual sepeda motor bekas antara lain : menambahkan variabel input yakni faktor-faktor lain yang mempengaruhi harga jual sepeda motor bekas, misalnya jarak tempuh dan minat pasar. Serta mengklasifikasikan sepeda motor berdasarkan jenis dan merk motor. Dalam penelitian ini hanya menggunakan tipe fungsi keanggotaan segitiga, fungsi keanggotaan trapesium, dan fungsi keanggotaan diskrit. Untuk penelitian berikutnya dapat digunakan fungsi keanggotaan lainnya dan memperhatikan MAPE yang diperoleh semakin kecil atau semakin besar.
DAFTAR PUSTAKA
Andini, P. dan Rahardjo, S.T. 2012. Analisi Faktor-Faktor Yang Mempengaruhi Keputusan Pembelian Mobil Hyundai i20. Jurnal Manajemen. Vol. 1, No. 2, Hal. 105116. Fakultas Ekonomi dan Bisnis Universitas Diponegoro.
BPS. 2013. Statistik Transportasi 2013. Badan Pusat Statistik Indonesia.
Istraniady, Andrian, P. dan Mardiani. 2013. Analisis Perbandingan Metode Fuzzy Tsukamoto Dan Metode Fuzzy Mamdani Pada Perbandingan Harga Sepeda Motor Bekas. Palembang : Jurnal Teknik
Informatika STMIK GI MDP.
Harun, S. 1999. Forecasting and Simulation of Net Inflows for Reservoir Operation and Management. Malaysia : Thesis. Universiti Teknologi Malaysia.
Jang, J.S.R., Sun, C.T., dan Mizutani, E. 1997. Neuro-Fuzzy and Soft Computing. London : Prentice Hall.
Kusumadewi, S. dan Purnomo, H. 2010. Aplikasi Logika Fuzzy Untuk Pendukung Keputusan. Yogyakarta : Graha Ilmu.
Prasetya, I. dan Rahayu, Y. 2015. Penentuan Harga Jual Sepeda Motor Bekas Menggunakan Fuzzy Logic (Metode
Tsukamoto) dan Implementasinya. Jurnal Teknik Informatika, Fakultas Ilmu
Komputer Universitas Dian Nuswantoro.
Salikin, F. 2011. Aplikasi Logika Fuzzy dalam Optimasi Produksi Barang Menggunakan Metode Mamdani dan Metode Sugeno. Yogyakarta : Skripsi Universitas Negeri Yogyakarta.
Sunoto, I. dan Lukman. 2015. Sistem
Pendukung Keputusan Penentuan Harga Jual Sepeda Motor Bekas Dengan Pendekatan Logika Fuzzy Inference System Mamdani. Jurnal SIMETRIS, Vol. 6, No. 2, Hal. 309-314. Universitas Indraprasta PGRI.
Triyatno. 2014. Analisis Faktor-Faktor Yang Mempengaruhi Keputusan Konsumen Dalam Pembelian Sepeda Motor Honda. Surakarta : Skripsi Universitas
Muhammadiyah Surakarta.
182
Discussion and feedback