IMPLEMENTASI ALGORITMA CAT SWARM OPTIMIZATION DALAM MENYELESAIKAN JOB SHOP SCHEDULING PROBLEM (JSSP)
on
E-Jurnal Matematika Vol. 5 (3), Agustus 2016, pp. 90-97
ISSN: 2303-1751
IMPLEMENTASI ALGORITMA CAT SWARM OPTIMIZATION DALAM MENYELESAIKAN JOB SHOP SCHEDULING PROBLEM (JSSP)
I Wayan Radika Apriana1§, Ni Ketut Tari Tastrawati2, Kartika Sari3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: viruezradikaviruez@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: taritastrawati@yahoo.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sari_kaartika@yahoo.co.id]
§Corresponding Author
ABSTRACT
Cat Swarm Optimization (CSO) algorithm is a metaheuristic algorithm which is based on two behaviors of cat, seeking and tracing. CSO algorithm is used in solving optimization problems. One of the optimization problems which can be seen in daily life is Job Shop Scheduling Problem (JSSP). This study aimed to observe the performance of CSO algorithm in solving JSSP. This study focused on 5 job-12 machine cases. According to this study, CSO algorithm was effective in solving real case of JSSP in 5 jobs – 12 machines scheduling at CV Mitra Niaga Indonesia agriculture tools industry. In implementing CSO algorithm in JSSP, a correct parameter choosing could lead to an optimal result. On other hand, the greater the number of jobs or machines the more complex and difficult the JSSP that needed to be solved.
Keywords : Cat Swarm Optimization, Job Shop Scheduling Problem, Makespan
Algoritma Cat Swarm Optimization (CSO) merupakan salah satu algoritma metaheuristik yang diusulkan oleh Shu-Chu Chu dan Pei-Wei Tsai pada tahun 2006. Dasar pemikiran algoritma ini adalah memanfaatkan kombinasi perilaku kucing yaitu seeking mode dan tracing mode untuk memecahkan masalah optimasi. Seeking mode menggambarkan keadaan kucing pada saat beristirahat, melihat kondisi sekitarnya mencari posisi berikutnya untuk bergerak. Tracing mode menggambarkan keadaan ketika kucing sedang mengikuti jejak targetnya (Chu & Tsai, 2007).
Algoritma Cat Swarm Optimization (CSO) dapat diimplementasikan dalam meyelesaikan permasalahan optimasi. Salah satu permasalahan optimasi yang ada dalam kehidupan sehari-hari adalah kasus Job Shop Scheduling Problem (JSSP). JSSP adalah salah permasalahan yang biasanya dihadapi perusahaan yang bergerak di bidang industri manufaktur. JSSP merupakan
permasalahan optimasi kombinatorial yang bertujuan untuk mendapatkan urutan terbaik operasi mesin-mesin dengan waktu penyelesaian seluruh pekerjaan (makespan) yang minimum (Suyanto, 2010).
Beberapa penelitian menggunakan algoritma optimasi dalam menyelesaikan kasus JSSP. Satrio (2007) meneliti masalah optimasi penjadwalan job shop untuk industri peralatan pengolahan hasil pertanian dengan menggunakan algoritma genetika. Pratama (2009) meneliti masalah optimasi penjadwalan job shop menggunakan metode Particle Swarm Optimization (PSO) yang dimodifikasi. Bouzidi & Riffi (2014) mengimplementasikan algoritma CSO dalam menyelesaikan kasus JSSP.
Dari penelitian-penelitian yang dipaparkan pada bagian terdahulu, diperoleh bahwa algoritma genetika efisien dalam menyelesaikan kasus JSSP berskala kecil maupun berskala besar. Sementara algoritma PSO yang dimodifikasi memiliki kinerja yang baik dalam menyelesaikan kasus dengan jumlah mesin tidak
lebih dari 10 mesin. Selain itu juga diperoleh bahwa algoritma CSO dapat menghasilkan solusi yang baik dilihat dari waktu yang diperlukan dan solusi terbaik yang dicapai dalam menyelesaikan kasus JSSP yang datanya diperoleh dari OR-Library.
Oleh karena itu peneliti tertarik untuk mengkaji kinerja algoritma CSO untuk menyelesaikan kasus nyata JSSP. Data yang digunakan adalah data dari penelitian Satrio (2007) kasus penjadwalan 3 job – 2 mesin yaitu kasus yang dibuat mengikuti aturan permasalahan penjadwalan tipe job shop yang digunakan untuk validasi program dan kasus penjadwalan 5 job – 12 mesin yaitu kasus di industri peralatan pengolahan hasil pertanian CV Mitra Niaga Indonesia, Bogor. Pada penelitian ini diharapkan bisa menjadi cara alternatif solusi dalam menyelesaikan kasus nyata JSSP.
Job shop scheduling problem (JSSP) adalah permasalahan optimasi kombinatorial. Misalkan terdapat n buah job atau pekerjaan, yaitu Jx ,J2,…,Jn yang akan diproses pada m buah mesin, yaitu My , ^2 ,…,Mm . Waktu yang diperlukan untuk operasi Oij (mengerjakan job Ji dengan menggunakan mesin Mj ) adalah tij . Setiap operasi diproses selama waktu tertentu dan oleh mesin tertentu. Setiap mesin hanya dapat menangani satu operasi, dan operasi dari pekerjaan yang sama tidak dapat diproses secara bersamaan. Tujuan dari job shop scheduling adalah bagaimana membuat jadwal yang berupa urutan pengerjaan yang optimal berdasarkan kriteria tertentu, misalkan untuk mendapatkan jadwal dengan makespan yang minimum (Suyanto, 2010).
Formulasi Masalah Job Shop Statik, untuk permasalahan n job dan m mesin (m,n∈N), solusinya diperoleh dari urutan n×m proses. Masing-masing solusi diwakili oleh urutan semua operasi yang ada. Operasi yang dimaksud adalah operasi pertama sampai operasi ke-k(k≤n×m), k∈N. Setiap proses diwakili oleh sepasang M0. dan T0.,i∈{1,2,…,k} (Bouzidi & Riffi, 2014).
Misalkan aj ∈ { Oy,O ,…,Oji (k≤n ×m)} dan j ∈{1,2,…,k }, j∈N . Bentuk solusi umum JSSP yang diperoleh dari urutan n×m proses dapat dilihat pada Gambar 1.
|
a1 |
¾ |
Oik (k≤n ×m) |
Gambar 1. Bentuk solusi umum JSSP
Dalam membuat jadwal yang valid, langkah pertama yang harus dilakukan adalah data dari kasus JSSP dibuat ke dalam bentuk matriks informasi. Matriks informasi dibuat untuk mewakili informasi dari masing-masing operasi dan sebagai dasar dalam membuat penjadwalan yang memenuhi setiap batasan yang ada (valid). Matriks informasi memiliki k(k≤n×m) kolom dan lima baris. Kolom mewakili jumlah total operasi yang ada pada seluruh job dan kelima baris yang dimaksud adalah
Oi : nama atau nomor operasi di jadwal
(i ∈{1,2,…,k}).
JOj : job dari operasi Oi .
Seoioi : urutan dari operasi Oi dengan job yang sesuai.
Mq1 : mesin dimana operasi Oi akan diproses.
T0. : waktu proses dari operasi Oi .
Bentuk matriks informasi dapat dilihat pada persamaan (1).
|
t O1 |
… |
Oi I |
… (k≤n ×m) | ||
|
⎛ |
… |
J0I • |
… (k≤n ×m) |
⎞ | |
|
⎜ SeQo1 |
… |
SeQot |
.. SβQQli (k≤n ×m) |
(1) | |
|
⎜ Mch |
… |
M0i ■ |
" Mok (k≤n ×m) | ||
|
⎝ ^ |
… |
Toi ■ |
' °k (k≤n ×m) |
⎠ | |
Cat Swarm Optimization (CSO) adalah algoritma yang diusulkan oleh Shu-Chuan Chu dan Pei-Wei Tsai pada tahun 2006. CSO dihasilkan melalui pengamatan terhadap perilaku sekumpulan kucing dan terdiri dari dua sub-models yaitu : ”seeking mode” dan ”tracing mode” (Chu & Tsai, 2007).
Tahap pertama yang dilakukan pada proses CSO adalah menentukan berapa banyak kucing yang digunakan dalam iterasi, selanjutnya menggunakan kucing dalam CSO untuk
menyelesaikan masalah. Setiap kucing memiliki posisi yang tersusun di dalam dimensi M, kecepatan untuk setiap dimensi, nilai fitness yang menunjukan penyesuaian kucing pada fungsi fitness dan bendera untuk menentukan kucing masuk berada dalam seeking mode atau tracing mode. Solusi akhir adalah satu kucing dengan posisi terbaik. CSO akan menyimpan solusi terbaik hingga akhir iterasi (Chu & Tsai, 2007).
CSO terdiri dari dua sub model yaitu seeking mode dan tracing mode, untuk mengkombinasikan kedua mode dalam satu algoritma, perlu didefinisikan mixture ratio (MR). Dengan mengamati perilaku kucing, dapat diketahui bahwa kucing menghabiskan sebagian besar waktunya untuk beristirahat.
Selama beristirahat, kucing mengubah posisinya secara perlahan dan berhati-hati, terkadang tetap pada posisi awalnya. Untuk menerapkan perilaku ini ke dalam CSO, digunakan seeking mode. Perilaku mengejar target diaplikasikan dalam tracing mode. Oleh karena itu, MR harus bernilai kecil untuk memastikan bahwa kucing menghabiskan sebagian besar waktu kucing dalam posisi seeking mode (Chu & Tsai, 2007).
-
a. Seeking Mode
Mode ini menggambarkan keadaan kucing pada saat beristirahat, melihat kondisi sekitarnya mencari posisi berikutnya untuk bergerak. Seeking mode memiliki empat faktor penting yang harus diperhitungkan, yaitu : seeking memory pool (SMP), seeking range of the selected dimension (SRD), counts of dimension to change (CDC), dan self position considering (SPC). SMP digunakan untuk menentukan berapa banyak jumlah kucing tiruan yang akan dibuat, SRD atau mencari rentang dimensi terpilih, CDC menentukan dimensi yang akan berubah, dan SPC mempertimbangkan apakah posisi saat ini menjadi salah satu kandidat (Chu & Tsai, 2007).
Langkah-langkah seeking mode dapat dideskripsikan dalam 5 tahap sebagai berikut (Chu & Tsai, 2007):
Langkah 1: Bangkitkan j tiruan dari posisi kucing ke- k, dengan j = SMPj Jika nilai SPC
benar, maka j = (SMP — 1), kemudian pertahankan posisi saat ini sebagai salah satu kandidat.
Langkah 2: Untuk setiap tiruan, disesuaikan dengan CDC, tambahkan atau kurangkan SRD persen dari nilai saat ini secara acak dan gantikan nilai yang sebelumnya.
Langkah 3: Hitung nilai fitness (FS) untuk semua titik kandidat.
Langkah 4: Jika semua nilai fitness tidak benar-benar sama, hitung probabilitas terpilih masing-masing titik kandidat dengan menggunakan persamaan (2), sebaliknya atur probabilitas terpilih untuk semua titik sama dengan 1.
Ph = , dimana 0<h< j (2)
Langkah 5: secara acak pilih titik untuk bergerak dari titik-titik kandidat, dan pindahkan posisi kucing ke- .
Jika tujuan fungsi fitness adalah untuk menemukan solusi minimal, maka SSb = FSmax, sebaliknya SSb = FSmtn (Bouzidi & Riffi, 2014).
-
b. Tracing Mode
Tracing mode adalah mode yang menggambarkan keadaan ketika kucing sedang mengikuti jejak targetnya. Sekali kucing memasuki tracing mode, kucing tersebut akan bergerak sesuai dengan kecepatannya untuk tiap dimensi (Chu & Tsai, 2007).
Tahapan tracing mode dapat dijabarkan dalam 3 langkah sebagai berikut (Chu & Tsai,2007):
Langkah 1: Perbarui nilai kecepatan untuk setiap dimensi (Vk,d) dengan rumus
-
V' K a = Vk, d + r1×c1 (Xb es t , d — Xk, d) (3)
Langkah 2: Periksa apakah kecepatan berada dalam rentang kecepatan maksimum. Jika kecepatan yang baru melebihi rentang, tetapkan nilai sama dengan batas.
Langkah 3: Perbarui posisi kucing ke- k dengan rumus
X ' k, d = Xk, d + V' k, d (4)
Xb es t, d adalah posisi kucing yang memiliki nilai fitness terbaik, Xk,d adalah posisi kucing ke- k pada dimensi ke- , adalah konstanta dan adalah nilai acak dalam rentang [0,1].
Inertia Weight (w)
Parameter ini berguna untuk mengontrol keseimbangan antara kemampuan eksplorasi global dan lokal, serta penurunan kecepatan untuk menghindari stagnasi pada optimum lokal. Jika nilai inertia weight terlalu besar akan mengakibatkan posisi kucing berubah terlalu jauh, sehingga gagal untuk menemukan solusi. Sebaliknya, jika nilai inertia weight terlalu kecil posisi kucing akan terjebak pada optimum lokal (Chu & Tsai, 2007).
Untuk menyelesaikan permasalahan kucing yang menjauhi solusi dan terperangkap pada optimum lokal, CSO dimodifikasi dengan menambahkan parameter baru berupa nilai inertia weight (w) yaitu, CSO dengan inertia. Pada nilai inertia weight ( ) berubah secara
acak dalam tracing mode, sehingga kecepatan pada persamaan (3) menjadi:
V'k,d = w× Vk,d + ^i × c1χXbest, d - χk,d) (5)
Data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari penelitian Satrio (2007) mengenai job shop scheduling problem. Jenis data yang digunakan adalah data kuantitatif, terdiri dari tiga kasus job shop. Kasus yang digunakan dalam penelitian ini adalah kasus pertama yaitu, penjadwalan 3 job – 2 mesin dan kasus ketiga yaitu, penjadwalan 5 job – 12 mesin. Kasus pertama dipilih untuk validasi program yang telah dibuat. Kasus ketiga adalah kasus penjadwalan di Industri peralatan pengolahan hasil pertanian.
Variabel yang digunakan dalam penelitian ini adalah waktu penyelesaian seluruh pekerjaan (makespan) dinotasikan dengan Cmax.
Langkah-langkah yang akan dilakukan dalam penelitian ini adalah:
-
1. Membuat solusi JSSP yang valid
-
a. Menyatakan data ke dalam bentuk matriks informasi berdasarkan (1).
-
b. Membuat solusi acak awal, solusi yang dihasilkan dapat berupa solusi valid atau berupa solusi yang tidak valid.
-
c. Jika solusi acak awal yang dihasilkan berupa solusi yang valid, lanjutkan
menghitung makespan solusi tersebut. Sedangkan jika solusi acak awal berupa solusi yang tidak valid, lakukan koreksi hingga mendapatkan solusi yang valid.
-
d. Menghitung makespan dari solusi yang valid.
-
2. Terapkan algoritma Cat Swarm Optimization dengan langkah-langkah sebagai berikut :
-
a. Bangkitkan sejumlah N kucing dalam proses. Setiap kucing merepresentasikan himpunan solusi awal, yaitu urutan acak dari operasi Oi sampai operasi Okl^k ≤ xxm), dimana n adalah job dan m adalah mesin.
-
b. Inisialisasi posisi, kecepatan, dan ruang kucing.
-
c. Hitung nilai fitness masing-masing kucing berupa makespan dari setiap solusi.
-
d. Pindahkan kucing sesuai rasio MR. Jika kucing berada dalam seeking mode perlakukan sesuai proses seeking mode, sebaliknya perlakukan sesuai proses tracing mode.
-
(a) Untuk kucing dalam seeking mode :
-
1. Bangkitkan tiruan sebanyak SMP yang telah ditetapkan. Jika SPC bernilai benar, maka pertahankan posisi saat ini sebagai salah satu kandidat.
-
2. Untuk setiap tiruan, tambahkan atau kurangkan sebesar SRD persen dari nilai saat ini, jika melebihi rentang SRD maka tetapkan nilai rentang sama dengan batas maksimum.
-
3. Hitung nilai fitness untuk semua titik kandidat.
-
4. Hitung peluang terpilih masing-masing titik kandidat dengan menggunakan persamaan (2).
-
5. Secara acak pilih titik untuk bergerak dari titik-titik kandidat, lalu pindahkan posisi kucing.
-
(b) Untuk kucing dalam tracing mode :
-
6. Perbaharui kecepatan kucing dengan menggunakan persamaan (5) dan perbaharui posisi kucing menggunakan persamaan (4).
-
e. Pilih lagi sejumlah kucing dan masukkan dalam tracing mode sesuai MR, sisanya masukkan ke dalam seeking mode.
-
f. Perhatikan kondisi akhir algoritma. Jika telah memuaskan dalam artian fungsi fitness bernilai kecil, maka hentikan program. Sebaliknya, jika belum maka ulangi langkah (c) hingga (e).
-
g. Akhir pada algoritma yang digunakan berupa nilai fitness terkecil.
-
h. Kucing yang terpilih sebagai solusi
terbaik adalah kucing yang dapat
memenuhi semua batasan yang ada (valid) dengan nilai fitness terkecil.
Implematasi algoritma CSO dalam menyelesaikan kasus JSSP dijalankan dengan aplikasi MATLAB 7.8.0 (R2009a) pada
Notebook dengan spesifikasi Intel Core i3-2310M. 2.1 GHz dengan RAM 2 GB.
Selanjutnya akan diberikan hasil dan pembahasan mengenai kinerja algoritma CSO dalam menyelesaikan kasus optimasi. Kasus yang digunakan adalah kasus penjadwalan 3 job – 2 mesin sebagai validasi program dan kasus nyata penjadwalan 5 job – 12 mesin. Terlebih dahulu dibahas membuat solusi JSSP awal yang valid untuk diterapkan pada algoritma CSO.
Membuat Solusi JSSP Awal Yang Valid
Solusi JSSP dapat dikatakan valid jika jadwal yang dihasilkan memenuhi batasan yang telah ditetapkan pada masing-masing kasus JSSP. Setiap solusi JSSP yang valid memiliki waktu penyelesaian seluruh pekerjaan (makespan). Solusi JSSP awal yang valid diterapkan pada algoritma CSO sebagai salah satu kucing, tujuannya untuk mendapatkan
solusi yang lebih optimal dengan makespan yang minimum. Langkah-langkah dalam membuat solusi JSSP awal yang valid adalah sebagai berikut:
Pertama, menyatakan data ke dalam bentuk matriks informasi. Data kasus penjadwalan 3 job – 2 mesin dan kasus penjadwalan 5 job – 12 mesin dinyatakan ke dalam bentuk matriks informasi menggunakan persamaan (1). Representasi matriks informasi kasus penjadwalan 3 job – 2 mesin seperti berikut:
123456
122112
Berlaku cara yang sama untuk membentuk matriks informasi pada kasus penjadwalan 5 job – 12 mesin.
Langkah selanjutnya, membuat solusi acak awal. Solusi acak awal adalah solusi yang dibuat di awal secara sembarang tanpa memperhatikan urutan dari mesin-mesin yang beroperasi, sehingga solusi tersebut tidak selalu valid dan perlu dikoreksi. Sebagai contoh solusi acak awal dari kasus penjadwalan 3 job – 2 mesin pada Gambar 2.
|
4 |
5 |
1 |
2 |
3 |
6 |
Gambar 2. Solusi acak awal 3 job – 2 mesin
Berlaku cara yang sama untuk membentuk solusi acak awal pada kasus penjadwalan 5 job – 12 mesin.
Jika solusi acak awal yang dihasilkan tidak valid, maka dilanjutkan ke proses koreksi. Solusi acak awal yang tidak valid dikoreksi sampai mendapatkan solusi yang valid. Proses koreksi dilakukan dengan memprioritaskan operasi awal dibandingkan operasi lainnya pada setiap job untuk dioperasikan terlebih dahulu hingga membentuk solusi baru yang valid. Untuk kasus penjadwalan 3 job – 2 mesin diperoleh solusi valid yang paling sederhana dengan mengurutkan operasi-operasi yang ada pada kasus tersebut seperti yang tampak pada Gambar 3.
|
1 |
2 |
3 |
4 |
5 |
6 |
Gambar 3. Solusi valid 3 job – 2 mesin
Untuk solusi valid kasus penjadwalan 5 job – 12 mesin dapat dilihat pada Gambar 4.
|
1 |
2 |
3 |
… |
28 |
29 |
Gambar 4. Solusi valid 5 job – 12 mesin
Apabila solusi valid telah diperoleh, langkah selanjutnya adalah menghitung makespan dari jadwal yang sudah valid. Makespan dari solusi valid kasus penjadwalan 3 job – 2 mesin adalah 19 satuan waktu, seperti yang diperlihatkan oleh GANT chart di Gambar 5 dengan masing-masing warna mewakili operasi dengan job yang sama.
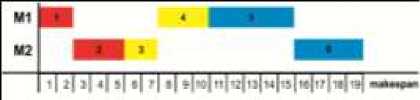
Gambar 5. GANT Chart solusi valid 3 job – 2 mesin
Dengan cara yang sama dalam menghitung makespan pada kasus penjadwalan 3 job – 2 mesin, untuk solusi valid kasus penjadwalan 5 job – 12 mesin diperoleh makespan sebesar 4462 menit. Lebih lanjut lagi untuk mendapatkan jadwal dan makespan yang optimal diterapkan algoritma CSO.
Menerapkan Algoritma Cat Swarm Optimization
Solusi JSSP awal yang valid digunakan sebagai salah satu kucing dalam menerapkan algoritma CSO. Kucing yang digunakan dalam kasus penjadwalan 3 job – 2 mesin memiliki posisi seperti Gambar 3. Sedangkan posisi kucing yang digunakan dalam kasus penjadwalan 5 job – 12 mesin dapat dilihat pada Gambar 4.
Selanjutnya menentukan kombinasi parameter yang digunakan CSO untuk mendapatkan nilai fitness terbaik melalui uji parameter. Uji parameter bertujuan untuk menentukan kombinasi parameter yang tepat dalam menemukan nilai fitness terbaik untuk masing-masing kasus. Parameter awal yang
digunakan dalam uji parameter adalah : MR = 0,02 ; SMP = 5 ; SRD = 0,2 ; CDC = 0,8 ; C1 = 2 yang diambil dari penelitian Chu & Tsai (2007) dengan asumsi N kucing = 30 dan iterasi sebanyak 2000. Pengujian dilakukan pada parameter MR, SMP, SRD, CDC, dan C1. Nilai masing-masing parameter yang akan di uji diambil dari penelitian-penelitian sebelumnya yang menerapkan algoritma CSO dalam menghasilkan nilai fitness yang baik.
Hasil pengujian untuk kombinasi parameter terbaik kasus penjadwalan 3 job – 2 mesin dapat dilihat pada Tabel 1.
Tabel 1. Kombinasi Parameter Terbaik Kasus
Penjadwalan 3 Job – 2 Mesin
|
MR |
0,3 |
|
SMP |
1 |
|
SRD |
0,6 |
|
CDC |
0,8 |
|
C1 |
2 |
|
R |
[0,1] |
Sedangkan hasil pengujian kombinasi parameter untuk kasus penjadwalan 5 job – 12 mesin dapat dilihat pada Tabel 2.
Tabel 2. Kombinasi Parameter Terbaik Kasus Penjadwalan 5 Job – 12 Mesin
|
MR |
0,5 |
|
SMP |
1 |
|
SRD |
0,4 |
|
CDC |
0,6 |
|
C1 |
1 |
|
R |
[0,1] |
Pada Tabel 1 dan Tabel 2 setiap parameter dipilih berdasarkan makespan dan running time terbaik yang dihasilkan. Pertama dilihat dari makespan yang terkecil, jika hasil makespan sama maka dilihat dari running time program dengan waktu tercepat.
Penjadwalan 3 Job – 2 Mesin
Posisi kucing yang digunakan adalah posisi kucing seperti Gambar 4.20 dengan kombinasi parameter-parameter terbaik yang telah diperoleh sebelumnya pada uji parameter, yaitu : MR = 0,3 ; SMP = 1 ; SRD = 0,6 ; CDC = 0,8 ; C1 = 2 ; R = [0,1]. Banyak kucing yang
digunakan dalam simulasi ini adalah 30 dan 50 dengan masing-masing kucing beriterasi sebanyak 500, 1000, dan 2000. Tujuannya untuk melihat apakah perubahan jumlah kucing dan iterasi dapat mempengaruhi hasil dari algoritma CSO dalam menyelesaikan kasus JSSP.
Hasil simulasi algoritma CSO dalam menyelesaikan kasus penjadwalan 3 job – 2 mesin dapat dilihat pada Tabel 3 dan Tabel 4.
Tabel 3. Hasil Simulasi 1 Algoritma CSO Pada Kasus Penjadwalan 3 Job – 2 Mesin.
|
Jumlah Kucing |
Iterasi |
Makespan |
Running Time |
Posisi Kucing |
|
N |
500 |
14 |
0,8594 |
1-3-2-4-5-6 |
|
kucing |
1000 |
19 |
1,7031 |
1-2-3-4-5-6 |
|
= 30 |
2000 |
11 |
3,4063 |
1-3-5-2-4-6 |
|
N |
500 |
11 |
1,3438 |
1-2-3-5-4-6 |
|
kucing |
1000 |
11 |
2,6875 |
1-3-2-5-4-6 |
|
= 50 |
2000 |
19 |
5,3750 |
1-2-3-4-5-6 |
Tabel 4. Hasil Simulasi 2 Algoritma CSO Pada Kasus Penjadwalan 3 Job – 2 Mesin.
|
Jumlah Kucing |
Iterasi |
Makespan |
Running Time |
Posisi Kucing |
|
N |
500 |
11 |
0,8594 |
1-2-3-5-4-6 |
|
kucing |
1000 |
19 |
1,7031 |
1-2-3-4-5-6 |
|
= 30 |
2000 |
11 |
3,2813 |
1-5-2-3-4-6 |
|
N |
500 |
19 |
1,3906 |
1-2-3-4-5-6 |
|
kucing |
1000 |
14 |
2,7031 |
1-3-2-4-5-6 |
|
= 50 |
2000 |
19 |
5,3594 |
1-2-3-4-5-6 |
Dari simulasi algoritma CSO pada kasus penjadwalan 3 job – 2 mesin diperoleh makespan terkecil, yaitu 11 satuan waktu dengan running time 0,8594 pada simulasi 2. GANT chart dengan posisi kucing [1-2-3-5-4-6] dapat dilihat pada Gambar 6.
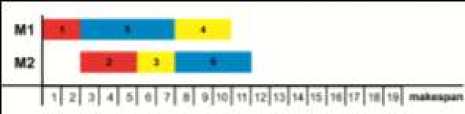
Gambar 6. Gant Chart Solusi Kasus Penjadwalan 3 Job – 2 Mesin
yang optimal dalam menyelesaikan kasus penjadwalan 3 job – 2 mesin.
Penjadwalan 5 Job – 12 Mesin
Pada kasus penjadwalan 5 job – 12 mesin, digunakan posisi kucing seperti Gambar 4 sebagai salah satu kucing dalam menerapkan algoritma CSO. Kombinasi parameter-parameter yang digunakan yaitu MR = 0,5 ; SMP = 1 ; SRD = 0,4 ; CDC = 0,6 ; C1 = 1 ; R = [0,1]. Simulasi dilakukan hanya sekali dengan banyak kucing dan banyak iterasi yang sama seperti pada kasus 3 job – 2 mesin. Hasil yang diperoleh dari algoritma CSO dalam menyelesaikan kasus penjadwalan 5 job – 12 mesin dapat dilihat pada Tabel 5.
Tabel 5. Hasil Simulasi Algoritma CSO Pada Kasus Penjadwalan 5 Job – 12 Mesin.
|
Jumlah Kucing |
Iterasi |
Makespan |
Running Time |
Posisi Kucing |
|
N kucing = 30 |
500 |
4462 |
1,0781 |
1-2-3-…-28-29 |
|
1000 |
4462 |
2,0625 |
1-2-3-…-28-29 | |
|
2000 |
4462 |
4 |
1-2-3-…-28-29 | |
|
N kucing = 50 |
500 |
4462 |
1,6875 |
1-2-3-…-28-29 |
|
1000 |
4462 |
3,3125 |
1-2-3-…-28-29 | |
|
2000 |
4462 |
6,5625 |
1-2-3-…-28-29 |
Dari Tabel 5 terlihat bahwa simulasi dengan jumlah kucing dan jumlah iterasi yang berbeda menghasilkan makespan yang sama yaitu 4462 menit. Sedangkan dari running time terlihat bahwa semakin bertambah jumlah kucing dan jumlah iterasi yang digunakan, semakin lama running time yang diperlukan.
Makespan dari hasil simulasi algoritma CSO pada kasus penjadwalan 5 job – 12 mesin adalah 4462 menit dengan solusi penjadwalan [1-2-3-…-28-29], seperti diperlihatkan pada GANT chart di Gambar 7.
Hasil ini menunjukan bahwa program yang dibuat valid dan dapat digunakan untuk mengimplementasikan algoritma CSO dalam menyelesaikan kasus JSSP. Dari simulasi 1 dan simulasi 2, algoritma CSO dapat mencapai hasil
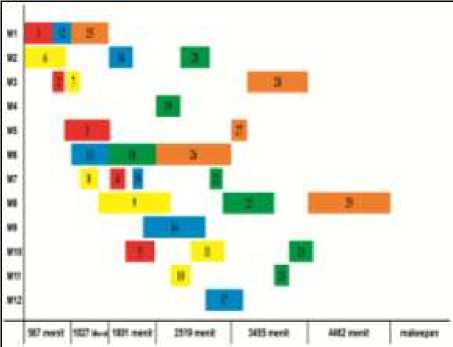
Gambar 7. Gant Chart Solusi Kasus Penjadwalan 5 Job – 12 Mesin
Hasil ini menunjukan bahwa makespan terkecil yang dapat diperoleh oleh algoritma CSO hanya sampai 4462 menit. CSO tidak bisa memperoleh hasil yang lebih optimal dari solusi JSSP awal yang valid kasus penjadwalan 5 job – 12 mesin dengan asumsi dan parameterparameter yang telah ditentukan sebelumnya.
Kesimpulan
Dari penelitian yang telah dilakukan, dapat disimpulkan bahwa algoritma CSO efektif dalam menyelesaikan kasus nyata JSSP untuk penjadwalan 5 job – 12 mesin di industri
peralatan pengolahan hasil pertanian CV Mitra Niaga Indonesia, Bogor. Dalam
mengimplementasikan algoritma CSO pada kasus JSSP, pemilihan nilai parameter yang tepat dapat menghasilkan solusi yang optimal. Selain itu, semakin besar jumlah job dan mesin yang digunakan maka semakin sulit dan rumit permasalahan JSSP yang harus diselesaikan.
Saran
Adapun saran yang perlu disampaikan pada penelitian ini mengenai hasil dan metode yang digunakan adalah :
-
1. Solusi awal untuk algoritma CSO dapat dibuat secara acak atau dengan menggunakan metode tertentu. Pembuatan solusi acak awal berpeluang menghasilkan solusi yang tidak valid, terutama pada kasus yang berukuran besar. Oleh karena itu,
untuk solusi awal dibuat menggunakan metode tertentu yang dapat menghasilkan solusi awal yang valid.
-
2. Dalam meyelesaikan kasus JSSP diperlukannya modifikasi metode CSO untuk dapat mencari solusi yang lebih optimal pada kasus dengan jumlah dimensi kucing yang besar. Perlu ditambahkan batasan pada random yang dijalankan metode CSO, dimana operasi awal pada setiap job diprioritaskan dari operasi berikutnya. Sehingga random yang dijalankan oleh metode CSO tidak merusak urutan operasi setiap job.
DAFTAR PUSTAKA
Bouzidi, A., & Riffi, M. E., 2014. Cat Swarm Optimization to Solve Job Shop Scheduling Problem. IEEE, 202-205.
Chu, S.-C., & Tsai, P.-W., 2007. Computanial Intelligence Based On The Behavior Of Cats. International Journal of Innovative Computing, Information and Control, 163173.
Pratama, H. A., 2009. Optimasi Permasalahan Penjadwalan Job Shop Menggunakan Metode Particle Swarm Optimization Yang Dimodifikasi. http://digilib.its.ac.id/ITS-Undergraduate-3100010038113/8785/penjadwalan-job-shop. Diakses pada 18 April 2015
Satrio, A. B., 2007. Optimasi Masalah
Penjadwalan Job-Shop Untuk Industri Peralatan Pengolahan Hasil Pertanian Dengan Menggunakan Algoritma Genetika. http://repository.ipb.ac.id/handle/123456789 /2514. Diakses pada 18 April 2015
Suyanto. 2010. Algoritma Optimasi Deterministik atau Probabilitik.
Yogyakarta: Graha Ilmu.
97
Discussion and feedback