MENENTUKAN PORTOFOLIO OPTIMAL MENGGUNAKAN MODEL CONDITIONAL MEAN VARIANCE
on
E-Jurnal Matematika Vol. 5 (3), Agustus 2016, pp. 82-89
ISSN: 2303-1751
MENENTUKAN PORTOFOLIO OPTIMAL MENGGUNAKAN MODEL CONDITIONAL MEAN VARIANCE
I Gede Ery Niscahyana1§, Komang Dharmawan2, I Nyoman Widana3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: igedeeryniscahyana@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: dharmawan.komang@gmail.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: nwidana@yahoo.com]
§Corresponding Author
ABSTRACT
When the returns of stock prices show the existence of autocorrelation and heteroscedasticity, then conditional mean variance models are suitable method to model the behavior of the stocks. In this thesis, the implementation of the conditional mean variance model to the autocorrelated and heteroscedastic return was discussed. The aim of this thesis was to assess the effect of the autocorrelated and heteroscedastic returns to the optimal solution of a portfolio. The margin of four stocks, Fortune Mate Indonesia Tbk (FMII.JK), Bank Permata Tbk (BNLI.JK), Suryamas Dutamakmur Tbk (SMDM.JK) dan Semen Gresik Indonesia Tbk (SMGR.JK) were estimated by GARCH(1,1) model with standard innovations following the standard normal distribution N (0,1) and the t-distribution. The estimations were used to construct a portfolio. The portfolio optimal was found when the standard innovation used was t-distribution with the standard deviation of 1.4532 and the mean of 0.8023 consisting of 0.9429 (94%) of FMII stock, 0.0473 (5%) of BNLI stock, 0% of SMDM stock, 1% of SMGR stock.
Keywords: Portfolio, Optimal portfolio, Conditional Mean Variance Models.
Pasar modal erat kaitannya dengan kegiatan investasi, salah satunya pada investasi saham. Dunia investasi erat kaitannya dengan portofolio saham karena portofolio dapat dibentuk menggunakan rataan dan varian saham untuk menaksir risiko yang ditanggung investor.
Sebagai hasil dari penelitian mengenai “VaR Portofolio Optimal dengan membandingkan Metode Markowitz dan Mean Absolute Deviation” menjelaskan bahwa pada model Mean Variance tidak terdapat autokorelasi antar data dan model ini tidak cukup akurat sebagai tolak ukur risiko suatu portofolio (Sartono & Setiawan, 2006).
Pada model Mean Variance, dalam memodelkan rataan return dan varian saham tidak terdapat autokorelasi antar data yang mengakibatkan tidak diketahuinya model ini baik diterapkan atau tidak. Oleh karena itu, dikembangkannya model Conditional Mean
Variance karena dalam menerapkan model yang baik diharuskan adanya autokorelasi antar data (Wei, 2006). Model Conditional Mean Variance yang dapat melakukan simulasi secara teliti, dimana dalam membentuk model ini digunakan model AR (Autoregressive) untuk menaksir rataan return dan menggunakan model GARCH (Generalized Autoregressive Conditional Heteroskedasticity) untuk menaksir varian saham, sehingga pada tulisan ini dibahas tentang penentuan portofolio optimal dengan model Conditional Mean Variance.
Return merupakan hasil yang diperoleh dari investasi. Return dapat dihitung menggunakan rumus (Husnan, 2003):
Ri-'=lnfe) (1)
Expected return dihitung menggunakan rumus n
E (R ) = ∑R i, tPi, t (2)
t=ι
dengan , menyatakan return (tingkat pengembalian) saham i pada periode t, ,
menyatakan indeks harga saham i pada periode t, , menyatakan indeks harga saham i pada
periode t-1, E(Ri) menyatakan expected return atau nilai harapan tingkat pengembalian saham i, , menyatakan peluang relatif untuk
tiap keuntungan saham i pada periode t dan n menyatakan banyaknya data saham.
Varian saham dapat dihitung menggunakan rumus (Husnan, 2003):
rt = [(Ri, , -E(Ri))]
Standar deviasi saham dapat
(3) dihitung
(4)
menggunakan rumus:.
σi
=√ 1∑
(Ri -e(Ri))2
Model Autoregressive adalah model yang
menggambarkan bahwa variabel dependent dipengaruhi oleh variabel dependent itu sendiri pada periode-periode dan waktu-waktu sebelumnya. Secara umum model autoregressive ordo 1 (AR(1)) mempunyai bentuk (Sugiarto, 2000)
rt = +∅ιrt-ι + Zt (5)
dengan rt menyatakan return saham pada periode t, C menyatakan konstanta, ∅ 1
menyatakan koefisien atau parameter dari model autoregressive, rt-ι menyatakan nilai return saham pada periode t-1 , dan εt menyatakan residual pada periode t.
Model ARCH diperkenalkan oleh Engle pada tahun 1982, model ini digunakan untuk memperkirakan volatilitas dengan nilai residual ( ^t) tidak saling berautokorelasi. Bollerslev mengembangkan model ARCH menjadi model GARCH dimana residual ( ^t ) mengikuti model GARCH ( P, cI ) dengan cI merupakan orde ARCH dan P merupakan orde dari GARCH yang dapat dimodelkan sebagai (Bollerslev, 1986)
εt = v Q
⅛ = +∑Yjrt-j +∑ ^iεt-i (6)
j=ι i=i
dengan Yj adalah nilai parameter GARCH ke j dimana j=1,2,…,P sedangkan rt-j adalah nilai varians pada periode t-j . Masalah yang dihadapi dalam memodelkan data acak melalui model GARCH adalah menentukan koefisien K, Yj , at berdasarkan data acak yang sudah ada.
Portofolio dinyatakan sebagai sekumpulan aset yang dimiliki untuk tujuan ekonomis tertentu. Konsep dasar yang dinyatakan dalam portofolio adalah bagaimana mengalokasikan sejumlah dana tertentu pada berbagai jenis investasi yang akan menghasilkan keuntungan yang optimal (Harold, 1998). Expected return dari portofolio saham diformulasikan sebagai (Husnan, 2003)
E(Rp)=∑KiUiE(Ri) (7)
dengan ωi menyatakan proporsi dana yang diinvestasikan pada saham i, E(Ri) menyatakan expected return atau nilai harapan tingkat pengembalian saham i, E( Rp )menyatakan expected return dari portofolio saham dan n merupakan banyaknya data saham.
Pemilihan portofolio didekati dengan cara memilih portofolio yang memberikan keuntungan maksimum dengan risiko tertentu. Untuk risiko portofolio digunakan persamaan sebagai (Husnan, 2003). n
rt =∑rtrt
i=i
n n
+∑∑Ui Uj Gij ;i≠j (8) i=ιj=i
dengan ωi menyatakan proporsi dana yang
diinvestasikan pada saham i, σp menyatakan variansi portofolio, σi menyatakan variansi saham i, σij menyatakan kovarian saham i dengan saham j dan n merupakan banyaknya data saham.
Penentuan portofolio optimal menggunakan Model Conditional Mean Variance dengan langkah-langkah sebagai berikut:
-
1. Pengumpulan data harga saham pada
Fortune Mate Indonesia Tbk (FMII.JK),
Bank Permata Tbk (BNLI.JK), Suryamas Dutamakmur Tbk (SMDM.JK) dan Semen Gresik Indonesia Tbk (SMGR.JK) (www.finance.yahoo.com) periode 4 tahun dari 19 Februari 2011 sampai 19 Februari 2015.
-
2. Menentukan tingkat pengembalian (return) data penutupan harga dari masing-masing saham.
-
3. Mencari standar deviasi dan varian dari return penutupan harga masing-masing saham untuk melihat karateristik data.
-
4. Melihat autokorelasi pada plot ACF dan PACF pada masing-masing data return saham untuk melihat prilaku data apakah benar-benar acak atau tidak.
-
5. Melakukan uji diagnostik sebagai klarifikasi terhadap model yang akan diajukan apakah memiliki unsur autokorelasi atau tidak yang dikenal dengan Uji Ljung-Box.
-
6. Melihat adanya unsur heteroskedastik bersyarat pada plot ACF dan PACF kuadratik return portofolio saham serta melakukan pengujian menggunakan ARCH Effects.
-
7. Estimasi parameter pada model AR dan GARCH dengan menggunakan distribusi normal (Gaussian) dan distribusi-t.
-
3. HASIL DAN PEMBAHASAN
Pengolahan Data
Pada penelitian ini membahas tentang bagaimana menentukan portofolio optimal menggunakan model Conditional Mean Variance. Portofolio ini dibentuk berdasarkan pada saham-saham yang terdaftar pada Bursa Efek Jakarta (BEJ) dan memiliki keuntungan tinggi selama periode 19 Februari 2011 sampai 19 Februari 2015. Data saham yang digunakan adalah data saham Fortune Mate Indonesia Tbk (FMII.JK), Bank Permata Tbk (BNLI.JK), Suryamas Dutamakmur Tbk (SMDM.JK) dan Semen Gresik Indonesia Tbk (SMGR.JK) dengan jumlah periode dari masing-masing saham sebanyak 208 penutupan mingguan saham.
Untuk mengetahui saham yang memiliki keuntungan tinggi maka dilakukan proses analisis data. Proses analisis data yang dilakukan adalah memplot data tingkat pengembalian (return) masing-masing saham yang diperoleh dari data harga penutupan periode mingguan (close). Proses perhitungan tingkat pengembalian (return) diperoleh menggunakan persamaan (1).
8.
9.
10.
11.
12.
Memilih model terbaik di antara model dengan distribusi normal (Gaussian) dan distribusi-t menggunakan kriteria AIC (Akaike Information Criterion) dan BIC (Bayesian Information Criterion) yang terkecil.
Simulasi rataan return dan varian menggunakan nilai parameter yang diperoleh dari hasil estimasi model AR sebagai rataan bersyarat dan model GARCH sebagai varian bersyaratnya.
Menghitung nilai koefisien korelasi dan membentukan matriks varian kovarian.
Menghitung besarnya proporsi dana, expected return dan risiko portofolio.
Membuat Kurva Efficient Frontier.
Hasil return yang diperoleh dibuat dalam bentuk grafik. Grafik return dari harga penutupan periode mingguan untuk masing-masing saham ditunjukkan pada Gambar 1.
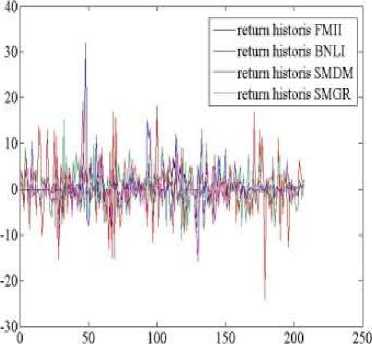
Penode
Gambar 1. Hasil Return Historis Masing-masing Saham
Dari perhitungan tingkat pengembalian (return) historis pada masing-masing saham, maka selanjutnya dicari nilai harapan tingkat pengembalian dengan persamaan (2).
n
E(Ri)=∑Ri,, t=l
dengan jumlah periode observasi mingguan T = 208, sehingga didapat hasil perhitungan sebagai berikut yang dimuat pada Tabel 1.
Tabel 1. Tabel Nilai Tingkat Pengembalian Harapan (expected return) Historis Saham
|
i |
Nama Saham |
E(Ri) |
|
1 |
FMII.JK |
0.7807 |
|
2 |
BNLI.JK |
-0.0109 |
|
3 |
SMDM.JK |
0.1078 |
|
4 |
SMGR.JK |
0.2671 |
Berdasarkan Tabel 1 dapat dilihat expected return historis dari keempat saham yaitu, saham BNLI.JK bernilai negatif artinya kemungkinan saham mengalami kerugian sedangkan, pada saham FMII.JK, saham SMDM.JK dan SMGR.JK berrnilai positif artinya saham mengalami keuntungan.
Perhitungan Varians dan Standar Deviasi Dari Data Historis Saham
Suatu investasi pada dasarnya selain menghasilkan keuntungan juga dapat memberikan risiko. Untuk mengetahui besar risiko dari masing-masing saham yang telah dipilih, dilakukan perhitungan varians dengan persamaan (3).
Oi = *(Ri,- ̅i)2+
dan standar deviasi untuk masing-masing saham dihitung dengan persamaan (4).
Tabel 2. Tabel Nilai Varians dan Standar Deviasi Historis Saham
|
i |
Nama Saham |
Oi |
O1 |
|
1 |
FMII.JK |
15.8333 |
3.9791 |
|
2 |
BNLI.JK |
8.7056 |
2.9505 |
|
3 |
SMDM.JK |
37.1975 |
6.0990 |
|
4 |
SMGR.JK |
18.7181 |
4.3264 |
Berdasarkan Tabel 2 dapat dilihat bahwa nilai varian dan standar deviasi historis dari saham SMDM.JK lebih tinggi daripada saham lainnya. Hal ini dapat diartikan saham SMDM.JK lebih berisiko daripada saham yang lainnya.
Model Conditional Mean Variance
Pada model Conditional Mean Variance terdapat dua metode yang digunakan yaitu metode AR untuk menaksir rataan bersyarat dan metode GARCH untuk menaksir varian bersyaratnya. Dalam menggunakan model Conditional Mean Variance ada beberapa langkah-langkah yang perlu diperhatikan sebagai berikut.
Tahap pertama adalah tahap pra-estimasi, pada tahap ini akan dilakukan uji autokorelasi dan uji heteroskedastisitas data. Uji ini dilakukan untuk mengetahui apakah model AR dan GARCH cukup baik diterapkan, karena asumsi yang digunakan dalam model mengharuskan adanya korelasi antar data. Untuk melihat apakah nilai tingkat keuntungan mingguan pada masing-masing saham berkorelasi, diperhatikan dari nilai autokorelasi tingkat keuntungan mingguan saham tersebut, untuk memudahkan dibuat plot ACF dan PACF dari data return mingguan ketiga saham yang terlihat pada Gambar 2, 3, 4, dan 5.
σ=
√ 1∑( .
-
̅ i )2
dengan jumlah periode observasi mingguan sebanyak 208 hari dengan hasil perhitungan yang dimuat pada Tabel 2.
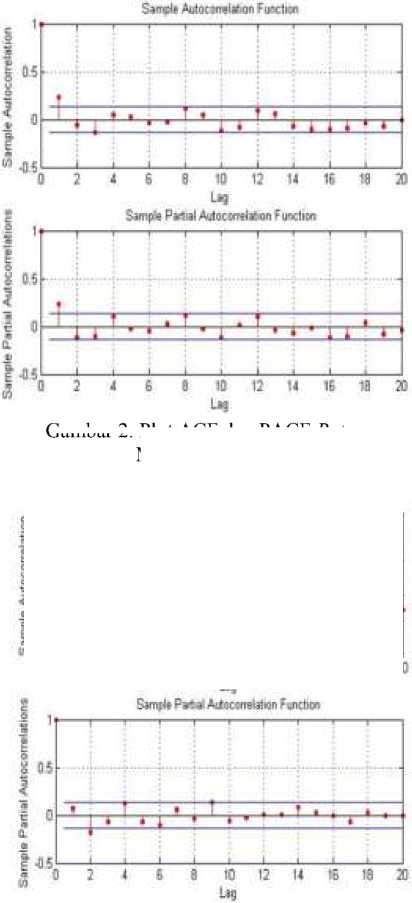
Gambar 3. Plot ACF dan PACF Return Mingguan Saham BNLI.JK
Gambar 2. Plot ACF dan PACF Return Mingguan Saham FMII.JK
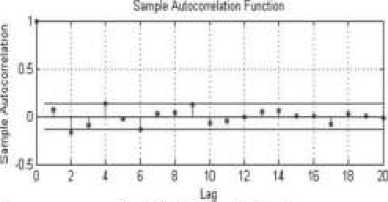
Gambar 5. Plot ACF dan PACF Return Mingguan Saham SMGR.JK
Plot ACF dan PACF pada gambar 2, 3, 4, dan 5 menunjukan sebagian besar autokorelasi keempat saham tidak bernilai nol dan terdapat data yang keluar dari lag atau batas yang artinya data berautokorelasi. Ini diperjelas dengan melakukan uji Ljung Box yang hasilnya dapat dilihat pada Tabel 3.
Tabel 3. Tabel Nilai p-value Masing- Masing Saham
|
No |
Saham |
p-value |
|
1 |
FMII.JK |
0.0048 |
|
2 |
BNLI.JK |
0.0224 |
|
3 |
SMDM.JK |
0.00026 |
|
4 |
SMGR.JK |
0.0133 |
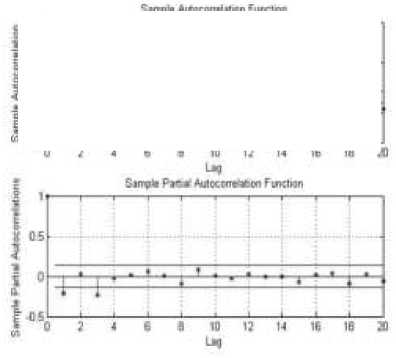
Gambar 4. Plot ACF dan PACF Return
Mingguan Saham SMDM.JK

Berdasarkan Tabel 3 dapat dilihat bahwa nilai p-value dari masing-masing saham lebih kecil dari a = 0,05 yang mengindikasikan terima H^ yang artinya data memiliki korelasi.
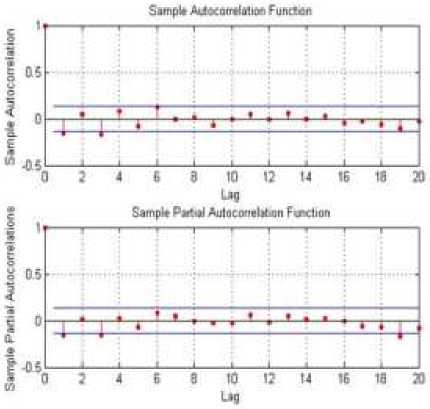
Selanjutnya untuk melihat adanya unsur heteroskedastik pada data return masing-masing saham dibuat seperti pada plot ACF dan PACF kuadratik return saham (MATLAB 2013,[4]) yang tampak pada Gambar 6.
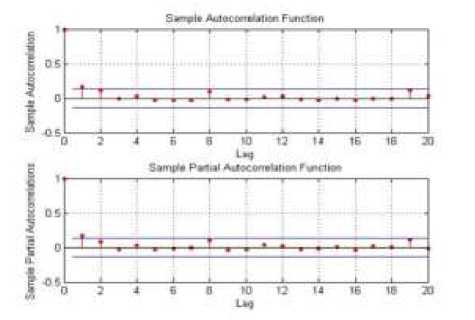
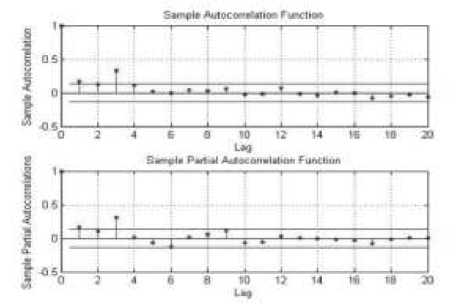
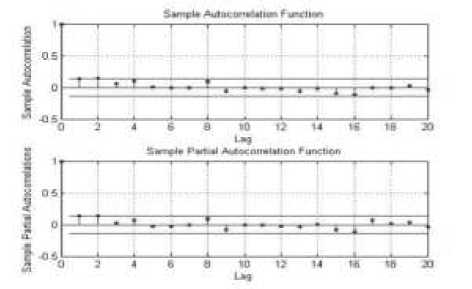
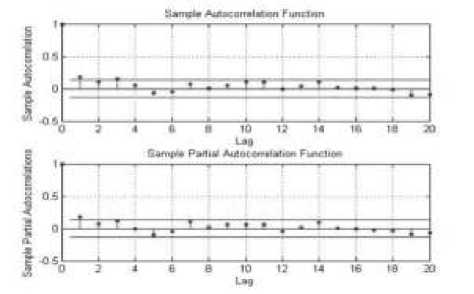
Gambar 6. Plot ACF dan PACF Kuadratik Return Mingguan Saham FMII.JK, BNLI.JK, SMDM.JK dan SMGR.JK
Dari plot ACF dan PACF kuadratik return dari masing-masing saham tampak bahwa setiap return saham memiliki unsur heteroskedastik.
Hasil ini dapat diperjelas dengan melakukan uji ARCH-LM yang dapat dilihat pada Tabel 4.
Tabel 4. Tabel Nilai p-value Masin-Masing Saham
|
No |
Saham |
p-value |
|
1. |
FMII.JK |
0.0262 |
|
2. |
BNLI.JK |
0.0177 |
|
3. |
SMDM.JK |
0.0261 |
|
4. |
SMGR.JK |
0.0111 |
Berdasarkan Tabel 4 dapat dilihat bahwa nilai p-value dari masing-masing saham lebih kecil dari a = 0,05 yang mengindikasikan terima H^ yang artinya data memiliki unsur heteroskedastisitas.
Setelah melihat dan menguji adanya autokorelasi dan unsur heteroskedastik pada return data saham selanjutnya dilakukan estimasi parameter model AR(1) dan GARCH (1,1) dengan menggunakan distribusi normal (Gaussian) dan distribusi-t. Salah satu distribusi dipilih melalui hasil yang didapat dari nilai AIC dan BIC terkecil.
Nilai AIC dan BIC dari estimasi kedua distribusi dapat dilihat pada Tabel 5.
Tabel 5. Hasil Nilai AIC dan BIC Dari Estimasi Kedua Distribusi.
|
No |
Saham |
Model |
AIC |
BIC |
|
1. |
FMII.JK |
Distribusi (Gaussian) |
1.0664 |
1.0831 |
|
Distribusi-t |
0.9023 |
0.9223 | ||
|
2. |
BNLI.JK |
Distribusi (Gaussian) |
1.0070 |
1.0237 |
|
Distribusi-t |
0.9862 |
1.0062 | ||
|
3. |
SMDM.JK |
Distribusi (Gaussian) |
1.3258 |
1.3425 |
|
Distribusi-t |
1.3111 |
1.3311 | ||
|
4. |
SMGR.JK |
Distribusi (Gaussian) |
1.1907 |
1.2107 |
|
Distribusi-t |
1.1898 |
1.2064 |
Dari Tabel 5 diperoleh nilai AIC dan BIC terkecil dimiliki oleh model distribusi-t.
Lebih lanjut lagi simulasi dilakukan untuk mengetahui nilai varian dan rataan return di masa yang akan datang pada masing masing saham. Hasil simulasi dari varian dan rataan return dapat dilihat pada Tabel 6.
Tabel 6. Hasil Simulasi Rataan Return dan Varian.
|
No |
Saham |
Rataan Return Simulasi |
Varian Simulasi |
|
1. |
FMII.JK |
0.7054 |
2.2325 |
|
2. |
BNLI.JK |
2.2912 |
40.6185 |
|
3. |
SMDM.JK |
5.1001 |
305.9427 |
|
4. |
SMGR.JK |
3.0018 |
65.5650 |
+2ωiω2(0.0104) +2ωiω3 (2.6221) +2ω1ω4(0.6385)+2^2 ^3 (22.7190) +2 ⅛)2^4(18.5134) + 2ω3ω4(21.3065)
Dari persamaan (8) dibentuklah matriks
varians-kovarians untuk mempermudah penyelesaian dalam mencari besarnya proporsi
dana yang diperlukan untuk penentuan return
portofolio dan risiko portofolio sebagaimana
Perhitungan Koefisien Korelasi
Berdasarkan hasil simulasi yang didapat dari metode AR dan GARCH dimana metode AR merupakan return besyarat dan GARCH merupakan varian bersyarat. Dari varian besyarat tersebut dibentuklah portofolio. Pada pembentukannya, diharuskan adanya keterkaitan atau korelasi antara data yang satu dengan yang lainnya. Hubungan antara saham yang satu dengan yang lainnya, dilihat dari nilai koefisien korelasi antara masing-masing saham. Nilai dari koefisien korelasi ini juga nantinya digunakan untuk membentuk matriks varian dan kovarian. Koefisien korelasi dari ketiga saham yang telah ditentukan dapat dilihat pada Tabel 7.
dirumuskan sebagai berikut:
=[ω1 ω2
2.2325
0.0104
2.6221
0.6385
0.0104
40.6185
22.7190
18.5134
2.6221
22.7190
305.9427
21.3065
0.6385
18.5134
21.3065
65.5650
-ω1∙
.ω4.
Tabel 7. Tabel Nilai Koefisien Korelasi antar Saham
|
P |
FMII.JK |
BNLI.JK |
SMDM.JK |
SMGR.JK |
|
FMII.JK |
1 |
0.0011 |
0.1003 |
0.0528 |
|
BNLI.JK |
0.0011 |
1 |
0.2038 |
0.3587 |
|
SMDM.JK |
0.1003 |
0.2038 |
1 |
0.1504 |
|
SMGR.JK |
0.0528 |
0.3587 |
0.1504 |
1 |
Penentuan Proporsi Dana
Proporsi dana merupakan persentase dari dana yang diinvestasikan pada saham-saham yang dimasukkan dalam portofolio. Besarnya proporsi dana yang didapat berpengaruh pada tingkat risiko dan return portofolio. Pada umumnya kombinasi proporsi dana yang terbaik adalah kombinasi proporsi dana yang menghasilkan portofolio dengan tingkat risiko terkecil dan dalam penginvestasian dana tersebut mencakup semua saham yang dimasukkan dalam portofolio. Nilai proporsi dana yang menghasilkan risiko terkecil didapat dengan memiminimumkan varian portofolio dan dihitung dengan model kuadratik pada persamaan (6), sebagai hasil perhitungan diperoleh seperti pada Tabel 8.
Dari Tabel 7 terlihat bahwa nilai koefisien korelasi antar masing-masing saham bernilai positif yang berarti varian dan return kedua saham akan bergerak ke arah yang sama.
Membentuk Matriks Varians-Kovarians
Nilai dari koefisien korelasi yang telah didapat, digunakan untuk membentuk matriks varian dan kovarian sebagai penentuan fungsi tujuan dari portofolio. Sebelum membentuk matriks varian dan kovarian maka terlebih dahulu dibentuk model matematika untuk mencari risiko portofolio sebagai berikut
σp = (2.2325) + ω22 (40.6185)
+ω32(305.9427) + ω42 (65.5650)
Tabel 8. Tabel Proporsi Dana Portofolio Optimal
|
Nama saham |
Proporsi dana |
|
FMII.JK |
0.9429 |
|
BNLI.JK |
0.0473 |
|
SMDM.JK |
0 |
|
SMGR.JK |
0.0096 |
Pada Tabel 8 dapat dilihat bahwa proporsi dana pada saham FMII.JK menunjukkan nilai terbesar dari saham yang lainnya. Hal ini dikarenakan saham FMII.JK menghasilkan tingkat keuntungan paling tinggi dari saham lain. Ini mengindikasikan dana yang diinvestasikan pada saham FMII.JK pada portofolio akan lebih menghasilkan keuntungan portofolio yang
optimal dibandingkan jika dana tersebut dikombinasikan dalam bentuk lain.
Perhitungan Tingkat Pengembalian Harapan (Expected Return) Portofolio dan Varian Portofolio
Hasil proporsi dana yang didapat selanjutnya digunakan untuk menghitung expected return dan varian portofolio. Hasil dari expected return dan varian portofolio berturut-turut sebesar 0.8023 dan 1.4532. Besarnya nilai varian portofolio lebih kecil daripada nilai varian dari masing-masing saham sebelum dimasukkan dalam portofolio yang merupakan ukuran risiko investasi. Hal ini dikarenakan risiko tersebut terdiversifikasi pada saham-saham lain dan tidak bertumpu hanya pada satu saham saja.
Simulasi Kurva Efficient Frontier
Setelah dilakukann perhitungan portofolio optimal dengan model Conditional Mean Variance maka dibentuk kurva efficient frontier untuk dapat mengetahui letak titik portofolio optimal yang dihasilkan. Gambar 7 menunjukan kurva efficient frontier pada distribusi Gaussian dan distribusi-t.
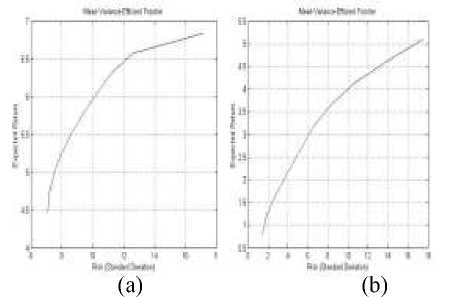
Gambar 7. Kurva Efficient Frontier dengan
Distribusi Gaussian (a) & Distribusi-t (b)
Berdasarkan Gambar 7 diperoleh bahwa portofolio optimal dengan model distribusi Gaussian berada pada titik (7.0851, 4.4683) sedangkan dengan model distribusi-t berada pada titik (1.4532, 0.8023). Dengan demikian portofolio optimal dengan model distribusi-t menghasilkan varian yang lebih kecil.
Berdasarkan hasil dan pembahasan yang telah diuraikan pada bab sebelumnya mengenai portofolio optimal menggunakan model Conditional Mean Variance dengan distribusi-t maka diperoleh nilai varian sebesar 1.4532 dan return sebesar 0.8023. Nilai varian minimum tersebut dihasilkan dari proporsi dana saham FMII.JK sebesar 94%, saham BNLI.JK sebesar 5%, saham SMDM.JK sebesar 0%, dan saham SMGR.JK sebesar 1%.
Disarankan pada penelitian berikutnya mencermati kondisi-kondisi ekonomi yang mempengaruhi harga saham. Hal ini dapat dilakukan dengan menggunakan data yang kondisi data ekonominya naik dan turun.
DAFTAR PUSTAKA
Bollerslev, T., 1986. Generalized Autoregresive Conditional Heterokedasticity. Journal of Econometric, pp.307-27.
Harold, B. J., 1998. A Utility Approach to The Portfolio Allocation Decision and The Investment Horizon. Journal of Portfolio Management.
Husnan, S., 2003. Dasar-Dasar Teori Portofolio dan Analisis Sekuritas. Yogyakarta: AMP YKN.
MATLAB dan Simulink. 2013. Specify Conditional Mean and Variance Models. http://www.mathworks.com/help/econ/condi tional-mean-and-variance-model-for-nasdaq-return.html diunduh tanggal 23 Maret 2015.
Sartono, R. A. dan Setiawan, A. A., 2006. VaR Portofolio Optimal: Perbandingan Antara Metode Markowitz dan Mean Absolute Deviation. Jurnal Siasat Bisnis, 11, pp. 3750.
Sugiarto, H., 2000. Peramalan Bisnis. Jakarta: PT. Gramedia Pustaka.
Wei, W., 2006. Time Series Analysis: Univariate and Multivariate Methods (Second ed.). New Jersey: Pearson Prentice Hall.
89
Discussion and feedback