ANALISIS PRIORITAS SOLUSI KEMACETAN LALU LINTAS DI KOTA DENPASAR DENGAN MENGGUNAKAN METODE ANALYTIC NETWORK PROCESS

E-Jurnal Matematika Vol. 5 (1), Januari 2016, pp. 7-13

ISSN: 2303-1751

ANALISIS PRIORITAS SOLUSI KEMACETAN LALU LINTAS DI KOTA DENPASAR DENGAN MENGGUNAKAN METODE ANALYTIC NETWORK PROCESS

Ni Wayan Nining Ismiranti^§1,I Putu Eka N. Kencana², I Komang Gde Sukarsa³

• ¹Jurusan Matematika Fakultas MIPA- Universitas Udayana [email: ning.ismiranti@gmail.com] ²Jurusan Matematika Fakultas MIPA- Universitas Udayana [email: i.putu.enk@gmail.com]

• ³Jurusan Matematika Fakultas MIPA- Universitas Udayana [email: sukarsakomang@yahoo.com] ^§Corresponding Author

ABSTRACT

The aim of this research is to find the alternative solutions that could be used to handle the traffic congestions in the Denpasar City and the priorities of each alternative. The main problem of this research is determining the appropriateness of alternatives and its criterias that could be used to set the priorities of the alternatives. Based on the interview with the transport experts of Denpasar City, there are three main factors that affect the traffic congestion i.e (1) the ratio of the volume of vehicles on the road capacity, (2) the existing traffic management, and the traffic regulation . The interviewee also suggest that there are six alternatives that can be used to handle traffic congestion. These alternatives are (1)improve the public transport system, (2) use technology to monitor and enforce the rules,(3) create a 3 in 1 rule, (4) create road pricing rule,(5) optimize the existing management in the road, and (6) create rule of road zoning. Based on the calculations by Analytic Network Process (ANP) method, improving the public transport system is the best alternative among others that is appropriate to handle traffic congestion in the Denpasar City.

Keywords: Analytic Network Process, Traffic Congestion, Priorities, Denpasar

• 1.    PENDAHULUAN

Metode ANP (Analytic Network Process) merupakan pengembangan dari Analytic Hierarcy Process (AHP) yang dikembangkan oleh Thomas L. Saaty yang digunakan untuk memilih alternatif terbaik dari sejumlah alternatif yang ada berdasarkan beberapa kriteria. Metode ANP menguraikan suatu masalah kedalam bentuk jaringan tanpa membuat asumsi elemen yang tingkatnya lebih tinggi dan elemen yang tingkatnya lebih rendah seperti yang terdapat pada AHP (Saaty & Vargas [3]).

Pada penelitian ini metode ANP akan digunakan untuk mencari prioritas alternatif-alternatif solusi yang bisa digunakan untuk menangani kemacetan lalu lintas di Kota Denpasar. Alternatif-alternatif solusi serta kriteria-kriteria yang akan digunakan diperoleh dari para narasumber yang merupakan para pengamat transportasi di Kota Denpasar.

Adapun alternatif-alternatif solusi yang akan dipaparkan merupakan alternatif solusi yang termasuk ke dalam manajemen lalu lintas tanpa pembangunan atau perluasan jalan.

ANP merupakan suatu teori pengukuran multycriteria yang digunakan untuk mendapat skala prioritas dari suatu penilaian individu yang termasuk ke dalam sebuah skala fundamental (Saaty [1]), seperti yang terdapat pada Tabel 1.

Tabel 1. Skala Fundamental

Intensitas Kepentingan	Penjelasan
1	Dua aktivitas berkontribusi secara sama besar
3	Kontribusi suatu aktivitas sedikit lebih besar dibandingkan yang lain
5	Kontribusi   suatu  aktivitas   lebih  besar dibandingkan yang lain
7	Kontribusi suatu aktivitas jauh lebih besar dibandingkan yang lain, aktivitas ini lebih dominan dilakukan dalam kenyataan
9	Fakta menunjukkan bahwa suatu aktivitas merupakan urutan tertinggi yang mungkin dalam suatu penegasan
2,4,6,8	Untuk kompromi nilai-nilai di atas

Langkah awal dari penggunaan metode ANP adalah dengan membentuk suatu model yang berbentuk sebuah jaringan yang saling dihubungkan dengan tanda panah. Jaringan tersebut menggambarkan hubungan saling ketergantungan antara komponen satu dan komponen yang lain dimana komponen yang berada di pangkal tanda panah memberikan pengaruh kepada komponen yang berada di ujung tanda panah, seperti Gambar 1.

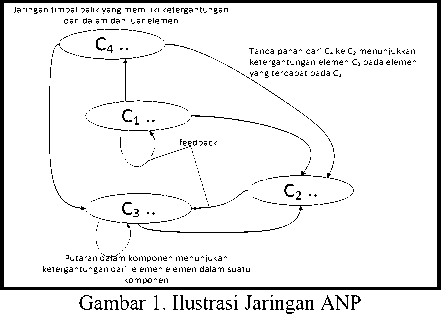
Selain dengan menggunakan jaringan, hubungan saling ketergantungan juga bisa digambarkan dengan menggunakan matriks seperti matriks berikut:

C

n × n

c11	c12	c1n
c21	c22	c2n
cn1	cn2	cnn

Ketergantungan setiap komponen pada suatu sistem dapat dibentuk dalam suatu matriks nol-satu C dengan sifat nilai 1 pada matriks diberikan apabila terdapat pengaruh yang diberikan komponen c terhadap komponen c dan nilai 0 diberikan apabila tidak ada pengaruh yang diberikan komponen c terhadap komponen c . Dalam hal ini c adalah nilai ketergantungan komponen c terhadap komponen c_i yang berisi nilai 0 atau 1, c_i adalah komponen yang memberikan pengaruh dan c adalah komponen yang dipengaruhi.

Pada penelitian menggunakan ANP seringkali digunakan lebih dari satu narasumber sebagai acuan. Hal ini akan memungkinkan diperolehnya pendapat yang berbeda mengenai bobot dari suatu perbandingan, akan tetapi metode ANP hanya memerlukan satu bobot untuk satu perbandingan dalam membentuk suatu matriks perbandingan berpasangan. Apabila hal ini terjadi maka bobot-bobot dari para narasumber harus dirata-ratakan dengan menggunakan persamaan geometric mean (Saaty & Vargas [3]).

1

a j = ( z 1.^z 2. — . ^zn ) n     "∙(¹)

Dengan a      : nilai rata-rata perbandingan

berpasangan kriteria A dengan A

Z_k     : nilai perbandingan yang diberikan

narasumber ke k , k =1,2,..., n n     : banyak narasumber

Matriks perbandingan berpasangan merupakan matriks berukuran n × n yang berisikan bobot perbandingan yang dilakukan terhadap elemen-elemen dalam suatu komponen dimana elemen-elemen ini memengaruhi suatu elemen lainnya. Misalkan terdapat suatu komponen C yang berisi elemen e₁₁, e₁₂,..., e_1n dan elemen-elemen tersebut

memberikan pengaruh terhadap elemen e₂₁ pada komponen C₂ , maka matriks perbandingan yang terbentuk adalah seperti berikut:

	■ 1	a12	••   a1 n
A=	a21 ;	1	-  a 2 n i
	. an 1	an2	•■      1

Nilai a pada perbandingan berpasangan merepresentasikan nilai kepentingan dari elemen kei terhadap elemen ke j pada komponen C₁ berkaitan dengan e₂₁ sebagai faktor kontrol. Nilai yang dimasukkan ke

dalam perbandingan merupakan nilai yang terdapat pada Tabel 1 dan pengisiannya dilakukan dengan prinsip resiprokal. Maksud dari resiprokal adalah jika diketahui nilai dari a maka secara otomatis nilai dari a akan ij                                                                               ji

sama dengan kebalikan dari a .

Setelah membentuk suatu matriks perbandingan A , selanjutnya akan dilakukan suatu proses pencarian eigen vector. Eigen vector diperoleh dari persamaan (Saaty & Vargas [3]):

A. w = ^λmax" w    -⁽²⁾

dengan

w     : eigen vector

λ     : eigen value terbesar

max

A     : matriks perbandingan berpasangan

Eigen vector yang diperoleh dari proses ini akan menjadi vektor prioritas dari elemen-elemen yang dibandingkan dalam matriks A .

Konsistensi dari setiap perbandingan berpasangan harus diuji, berikut adalah persamaan untuk menguji konsistensi dari matriks perbandingan berpasangan (Saaty & Vargas [3]). .

CR = —     ∙∙∙(3)

RI

Keterangan:

CR    : rasio konsistensi

CI    : index konsistensi

RI    : random consistency index

Index konsistensi diperoleh dengan rumus (Saaty & Vargas [3]):

₌ (^λmax - n) n -1

Nilai-nilai dari RI dapat dilihat pada Tabel 2

Tabel 2. Tabel Random Consistency Index

Orde	1	2	3	4	5	6	7	8	9	10
RI	0	0	0,52	0,89	1,11	1,25	1,35	1,40	1,45	1,49

Sumber: Saaty & Vargas, 2001, hal.9. [2]

Setiap matriks perbandingan dikatakan konsisten apabila nilaiCR tidak lebih dari 10%.

Setelah memastikan bahwa setiap matriks perbandingan berpasangan cukup konsisten,

langkah selanjutnya adalah membuat suatu supermatriks. Supermatriks berisikan vektor-vektor prioritas dari setiap perbandingan. Misalkan suatu sistem memiliki N komponen yaitu C₁, C₂,■■■, CN dan setiap komponen memiliki beberapa elemen. Komponen-komponen tersebut dihubungkan satu sama lain hingga terbentuk suatu model jaringan dari sistem yang diinginkan. Dari model tersebut akan dibentuk matriks-matriks perbandingan berpasangan yang masing-masing akan menghasilkan vektor prioritas. Nilai vektor prioritas dari setiap perbandingan dimasukkan pada kolom blok supermatriks yang bersesuaian. Blok-blok supermatriks tersebut akan disusun menjadi satu supermatriks seperti supermatriks berikut:

	" W11	W12	∙∙ W W1N
W =	W21 :	W22	∙∙ W 2N
	Wn 1	WN2	∙∙ W NN

Keterangan:

W : supermatriks yang terbentuk

W : matriks yang berisi bobot prioritas

elemen-elemen dalam komponen ke i terhadap elemen-elemen dalam komponen ke j .

Submatriks W yang terdapat dalam supermatriks disebut blok supermatriks. W merupakan sebuah matriks berukuran n_i × n_j seperti yang ditampilkan pada matriks berikut:

	(j 1) i1	wi(1j2)	( jn ) •■   wi1 j
Wij =	wi(2j1) :	wi(2j2)	(jni) ■w 2-
	. wj	wi(nj2)	( jn  ) ■’  Win  j

Keterangan:

w_ik ^l : nilai prioritas elemen kek dari komponen kei terhadap elemen ke l komponen ke j .

Setiap perhitungan yang dilakukan pada penelitian ini akan dilakukan dengan bantuan software super decision. Perangkat lunak super decision merupakan perangkat lunak yang digunakan untuk membantu pengambilan keputusan yang mengimplementasikan metode ANP.

• 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah data primer yang diperoleh melalui proses wawancara yang dilakukan terhadap para narasumber. Adapun narasumber yang menjadi acuan dalam penelitian ini adalah anggota satuan lalu lintas, dinas perhubungan serta para pengamat transportasi yang terdapat di Kota Denpasar.

Langkah-langkah penelitian yang dilakukan pada penelitian ini adalah sebagai berikut (Santoso, et al [4]):

• 1.    Tentukan narasumber yang akan diwawancarai.

• 2.    Melakukan     wawancara     terhadap

narasumber untuk memperoleh kriteria dan alternatif solusi yang sesuai untuk menangani kemacetan yang terjadi di Kota Denpasar.

• 3.    Membentuk model jaringan beradasarkan hasil wawancara yang di peroleh pada poin ke-2 serta menyusun angket beradasarkan model jaringan yang terbentuk.

• 4.    Melakukan     wawancara     terhadap

narasumber untuk mengetahui bobot dari masing-masing  kriteria dan alternatif.

Wawancara ini merupakan wawancara terstruktur dengan menggunakan angket yang telah dibuat.

• 5.    Membuat     matriks     perbandingan

berpasangan   yang   menggambarkan

pengaruh setiap elemen terhadap kriteria.

• 6.    Setelah semua bobot perbandingan terkumpul,      masukkan      nilai-nilai

kebalikannya serta nilai di diagonal utama kedalam     matriks      perbandingan

berpasangan, cari prioritas masing-masing kriteria dan uji konsistensinya.

• 7.    Cari vektor prioritas dari matriks yang dibuat pada langkah ke-6.

• 8.    Ulangi langkah 5, 6, dan 7 pada semua kriteria

• 9.    Buat unweighted supermatrix

• 10.    Buat weighted supermatrix

• 11.    Buat limmiting supermatrix.

• 12.    Ambil nilai dari alternatif yang dibandingkan untuk mengetahui hasil akhir perhitungan.

• 3.    HASIL DAN PEMBAHASAN

Tahap awal dari penelitian ini adalah pengambilan data yang menggunakan metode wawancara. Wawancara dilakukan untuk memperoleh faktor-faktor penyebab kemacetan lalu lintas serta solusinya.Wawancara ini dilakukan terhadap para narasumber yang merupakan para pengamat transportasi yang juga merupakan anggota Masyarakat Transportasi Indonesia (MTI) yang berada di Kota Denpasar. Setelah melakukan wawancara terhadap para pengamat transportasi maka diperoleh faktor-faktor penyebab kemacetan serta alternatif solusi yang bisa digunakan untuk menanganinya. Faktor-faktor serta alternatif solusi ini kemudian disusun menjadi suatu jaringan ANP seperti Gambar 2.

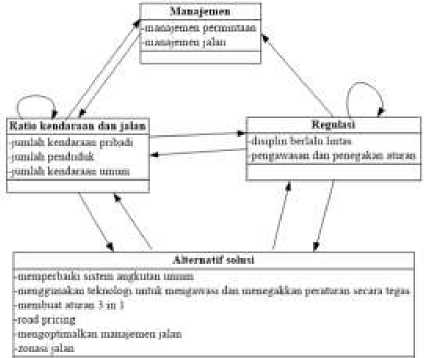
Gambar 2. Jaringan ANP yang terbentuk

Hubungan inner dependence dan outer dependence pada jaringan yang terdapat dalam Gambar 2 akan di ilustrasikan dalam matriks pada Gambar 3.

	Alternatif						Manajemen		Rasio			Regulasi
	A1	A2	A3	A4	A5	A6	MJ	MP	JK P	JKU	JP	D	PP
A1	0	0	0	0	0	0	0	0	1	1	0	1	1
A2	0	0	0	0	0	0	0	0	1	1	0	1	1
A3	0	0	0	0	0	0	0	0	1	1	0	1	1
A4	0	0	0	0	0	0	0	0	1	1	0	1	1
A5	0	0	0	0	0	0	0	0	1	1	0	1	1
A6	0	0	0	0	0	0	0	0	1	1	0	1	1
MJ	0	0	0	0	0	0	0	0	1	0	0	0	0
MP	0	0	0	0	0	0	0	0	1	0	0	0	0
JKP	1	1	1	1	1	1	1	1	0	0	0	0	1
JKU	1	1	1	1	1	1	1	1	1	0	0	0	1
JP	0	0	0	0	0	0	0	0	1	0	0	0	0
D	1	1	1	1	1	1	1	1	1	0	0	0	0
PP	1	1	1	1	1	1	1	1	1	0	0	1	1

Gambar 3. Tabel yang Berisi Matriks Ketergantungan

Dari matriks pada Gambar 3 akan dibentuk sebuah angket perbandingan. Angket tersebut digunakan sebagai alat bantu melakukan wawancara untuk memperoleh bobot dari setiap perbandingan. Bobot-bobot tersebut kemudian disusun menjadi matriks-matriks

perbandingan berpasangan sesuai dengan item pertanyaan yang terdapat pada angket. Setiap bobot dimasukkan ke dalam matriks perbandingan berpasangan dengan prinsip resiprokal yang kemudian dicari vektor prioritasnya.

Vektor-vektor prioritas tersebut kemudian disusun menjadi sebuah supermatriks. Dalam hal ini terdapat tiga buah supermatriks yang akan terbentuk yaitu: unweighted supermatrix, weighted supermatrix, dan limiting supermatrix. Unweighted supermatrix merupakan supermatriks yang dibuat dengan menyusun setiap vektor prioritas pada kolom yang sesuai, seperti Gambar 4.

	A1	A2	A3	A4	A5	A6	MJ	MP	JKP	JKU	JP	D	PP
A 1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.206	0.477	0.000	0.047	0.050
A 2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.073	0.047	0.000	0.308	0.355
A 3	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.065	0.093	0.000	0.103	0.091
A 4	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.166	0.122	0.000	0.224	0.201
A 5	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.223	0.111	0.000	0.119	0.155
A 6	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.267	0.150	0.000	0.199	0.150
MJ	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.500	0.000	0.000	0.000	0.000
MP	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.500	0.000	0.000	0.000	0.000
JKP	0.333	0.833	0.833	0.833	0.833	0.750	0.800	0.800	0.000	0.000	0.000	0.500	0.800
JKU	0.667	0.167	0.167	0.167	0.167	0.250	0.200	0.200	0.250	0.000	0.000	0.500	0.200
JP	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.750	0.000	0.000	0.000	0.000
D	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.750	0.000	0.000	0.000	0.000
PP	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.500	0.250	0.000	0.000	1.000	0.000

Gambar 4. Unwiehted Supermatrix

Tabel ini menunjukan prioritas tiap alternatif terhadap masing masing faktor. Dari tabel pada Gambar 4 diperoleh bahwa berdasarkan faktor JKP alternatif 6 mendapat bobot prioritas tertinggi yaitu 0,267, berdasarkan faktor JKU alternatif 1 mendapat bobot prioritas tertinggi yaitu 0,477, berdasarkan faktor disiplin dan faktor pengawasan alternatif 2 mendapat bobot tertinggi yaitu

0,308 dan 0,355. Gambar 4 ini hanya berisikan bobot perbandingan antar elemen, belum mencangkup perbandingan antar cluster (komponen). Oleh karena itu nilai-nilai yang terdapat pada Gambar 4 harus dikalikan dengan nilai-nilai pada perbandingan cluster untuk membentuk supermatiks baru yang disebut weighted supermatrix.

	A 1	A 2	A 3	A 4	A 5	A 6	MJ	MP	JKP	JKU	JP	D	PP
A 1	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.031	0.477	0.000	0.004	0.018
A 2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.011	0.047	0.000	0.029	0.128
A 3	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.010	0.093	0.000	0.010	0.033
A 4	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.025	0.122	0.000	0.021	0.072
A 5	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.034	0.111	0.000	0.011	0.056
A 6	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.041	0.150	0.000	0.019	0.054
MJ	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.136	0.000	0.000	0.000	0.000
MP	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.136	0.000	0.000	0.000	0.000
JKP	0.278	0.694	0.694	0.694	0.694	0.625	0.533	0.533	0.000	0.000	0.000	0.083	0.512
JKU	0.556	0.139	0.139	0.139	0.139	0.208	0.133	0.133	0.118	0.000	0.000	0.083	0.128
JP	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.354	0.000	0.000	0.000	0.000
D	0.083	0.083	0.083	0.083	0.083	0.083	0.167	0.167	0.077	0.000	0.000	0.000	0.000
PP	0.083	0.083	0.083	0.083	0.083	0.083	0.167	0.167	0.026	0.000	0.000	0.740	0.000

Gambar 5. Weighted Supermatrix

Nilai-nilai yang terdapat pada Gambar 5 merupakan nilai prioritas yang diperoleh dengan menggabungkan hasil perbandingan elemen dan perbandingan clutser. Gambar 5 memperlihatkan bahwa berdasarkan faktor JKP alternatif 6 mendapat bobot prioritas tertinggi yaitu 0,041, berdasarkan faktor JKU alternatif 1 mendapat bobot prioritas tertinggi yaitu 0,477, berdasarkan faktor disiplin dan faktor pengawasan alternatif 2 mendapat bobot tertinggi yaitu 0,029 dan 0,128. Nilai-nilai yang terdapat pada Gambar 5 digunakan untuk memeperoleh sepermatriks baru yang disebut limitting supermatrix.

Pada weighted supermatrix yang terdapat pada Gambar 5, alternatif yang mendapat prioritas tertinggi pada setiap faktor masih berbeda beda. Oleh karena itu supermatriks ini terus dipangkatkan sampai setiap kolom yang terdapat pada satu baris yang sama memiliki nilai yang sama dan membentuk supermatriks baru yang disebut limitting supermatrix. Supermatriks pada Gambar 5 dipangkatkan dengan tujuan untuk mencangkup semua hubungan saling memengaruhi yang mungkin terjadi pada setiap elemen dan alternatif, baik itu pengaruh langsung maupun pengaruh tak langsung.

	A 1	A 2	A 3	A 4	A 5	A 6	MJ	MP	JKP	JKU	JP	D	PP
A 1	0.091	0.091	0.091	0.091	0.091	0.091	0.091	0.091	0.091	0.091	0.000	0.091	0.091
A 2	0.027	0.027	0.027	0.027	0.027	0.027	0.027	0.027	0.027	0.027	0.000	0.027	0.027
A 3	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.000	0.023	0.023
A 4	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.000	0.037	0.037
A 5	0.035	0.035	0.035	0.035	0.035	0.035	0.035	0.035	0.035	0.035	0.000	0.035	0.035
A 6	0.044	0.044	0.044	0.044	0.044	0.044	0.044	0.044	0.044	0.044	0.000	0.044	0.044
MJ	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.000	0.039	0.039
MP	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.039	0.000	0.039	0.039
JKP	0.259	0.259	0.259	0.259	0.259	0.259	0.259	0.259	0.259	0.259	0.000	0.259	0.259
JKU	0.150	0.150	0.150	0.150	0.150	0.150	0.150	0.150	0.150	0.150	0.000	0.150	0.150
JP	0.102	0.102	0.102	0.102	0.102	0.102	0.102	0.102	0.102	0.102	0.000	0.102	0.102
D	0.061	0.061	0.061	0.061	0.061	0.061	0.061	0.061	0.061	0.061	0.000	0.061	0.061
PP	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.096	0.000	0.096	0.096

Gambar 6. Limiting Supermatrix

Limiting supermatrix akan memperlihatkan prioritas dari masing-masing alternatif beradasarkan seluruh kriteria yang ada. Langkah selanjutnya adalah menyusun alternatif-alternatif tersebut beradasarkan

prioritas yang diperoleh dari limiting supermatrix, seperti Tabel 3.

Tabel 3. Prioritas Alternatif

Alternatif	Nilai	Prioritas
Alternatif 1	0,091	1
Alternatif 6	0,044	2
Alternatif 4	0,037	3
Alternatif 5	0,035	4
Alternatif 2	0,027	5
Alternatif 3	0,023	6

Keterangan:

Alternatif 1: Memperbaiki sistem angkutan umum

Alternatif 2: Menggunakan teknologi untuk mengawasi dan menegakkan aturan

Alternatif 3: Membuat aturan

Alternatif 4: Membuat aturan road pricing Alternatif 5: Mengoptimalkan manajemen jalan

Alternatif 6: membuat aturan zonasi jalan

• 4.    KESIMPULAN DAN SARAN

Beradasarkan hasil yang diperoleh, dapat disimpulan bahwa alternatif-alternatif solusi yang dapat digunakan dalam menangani kemacetan lalu lintas di Kota Denpasar adalah memperbaiki sistem angkutan umum, menggunakan teknologi untuk mengawasi dan menegakkan aturan, membuat aturan 3 in 1, membuat     aturan     road     pricing,

mengoptimalkan manajemen jalan, membuat aturan zonasi jalan. Berdasarkan perhitungan menggunakan Metode ANP, dari keenam alternatif tersebut, alternatif terbaik yang bisa digunakan untuk menangani kemacetan lalu lintas di Kota Denpasar adalah alternatif memperbaiki sistem angkutan umum.

Dalam penelitian ini masih terdapat beberapa kekurangan salah satunya adalah analisis yang digunakan hanya menggunakan aspek traffic management analysis. Oleh karena itu pada penelitian selanjutnya bisa ditambahkan aspek-aspek lain dalam melakukan analisisnya misalnya aspek sosial dan budaya.

DAFTAR PUSTAKA

• [1]    Saaty. 2004. Fundamental of The Analytic Network Process Dependence and Feedback in Decision Making With a Singel Network. Journal of System Science and System Engineering, 129157.

• [2]    Saaty, T.L., & Vargas, L. G. 2001.

Models, Methods, Concepts and Applications of the Analytic Hierarchy Process. New York:    Springer

Science+Business Media New York.

• [3]    Saaty, T.L., & Vargas, L. G. 2006.

Decision Making With The Analytic Network Process Economic Political, Social and Technological Applications with Benefits, Opportunities, Cost and Risk (2  ed.). New York: Springer

Science+Business Media, LLC.

• [4]    Santoso, Leo Willyanto, Alexander Setiawan & Januar R. Stanley. 2009. Pembuatan Aplikasi Sistem Seleksi Calon Pegawai dengan Metode Analytic Network Process (ANP) di PT X. Teknik Informatika, Fakultas Teknologi Industri – Universitas Kristen Petra.

13