PENDUGAAN DATA HILANG DENGAN METODE YATES DAN ALGORITMA EM PADA RANCANGAN LATTICE SEIMBANG

E-Jurnal Matematika Vol. 4 (2), Mei 2015, pp. 74-82

ISSN: 2303-1751

PENDUGAAN DATA HILANG DENGAN METODE YATES DAN ALGORITMA EM PADA RANCANGAN LATTICE SEIMBANG

Ni Made Sariayu^§1, Made Susilawati², Kartika Sari³

¹Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: sarone00n@gmail.com] ²Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: susilawati.made@gmail.com] ³Jurusan Matematika, Fakultas MIPA - Universitas Udayana [Email: sari_kaartika@yahoo.co.id] ^§Corresponding Author

ABSTRACT

Missing data often occur in agriculture and animal husbandry experiment. The missing data in experimental design makes the information that we get less complete. In this research, the missing data was estimated with Yates method and Expectation Maximization (EM) algorithm. The basic concept of the Yates method is to minimize sum square error (JKG), meanwhile the basic concept of the EM algorithm is to maximize the likelihood function. This research applied Balanced Lattice Design with 9 treatments, 4 replications and 3 group of each repetition. Missing data estimation results showed that the Yates method was better used for two of missing data in the position on a treatment, a column and random, meanwhile the EM algorithm was better used to estimate one of missing data and two of missing data in the position of a group and a replication. The comparison of the result JKG of ANOVA showed that JKG of incomplete data larger than JKG of incomplete data that has been added with estimator of data. This suggest thatwe need to estimate the missing data. .

Keywords: Missing Data, Yates method, EM algorithm, Balanced Lattice Design.

1. PENDAHULUAN

Setiap rancangan percobaan sangat mungkin mengalami masalah data hilang. Data tersebut hilang disebabkan oleh beberapa hal yang tidak bisa diramalkan dan tidak bisa dihindari. Misalnya percobaan pada bidang pertanian, ketika hasil panen dari beberapa petak percobaan dirusak oleh hewan, hama dan lain-lain, dan juga pada bidang peternakan, ketika hewan mati saat percobaan, serta kejadian lainnya yang bisa saja muncul seperti salahnya pencatatan. Hilangnya data suatu percobaan akan menyebabkan hilangnya keterangan yang diperlukan sehingga informasi yang diperoleh kurang lengkap.

Pendekatan yang biasa digunakan untuk pendugaan data hilang antara lain adalah metode Yates, hot deck imputation, substitution, mean imputation, dan regression imputation (Black, et.al [1]). Pendekatan yang lebih modern untuk mengatasi data hilang di antaranya adalah algoritma Expectation Maximization (EM).

Penelitian pendugaan data hilang telah dilakukan oleh Fatimah [3], Widiharih [11], dan Sriliana [9]. Penelitian yang dilakukan oleh Fatimah [3], menggunakan metode Yates dan algoritma EM pada Rancangan Acak Kelompok (RAK) dan Rancangan Bujur Sangkar Latin (RBSL). Penelitian Widiharih [11], menggunakan metode Yates dan metode Bigger pada Rancangan Acak Kelompok Lengkap (RAKL). Kemudian penelitian yang dilakukan oleh Sriliana [9], menggunakan metode Yates pada Rancangan Bujur Sangkar Latin (RBSL).

Pada percobaan dengan banyak perlakuan, RAL, RAKL ataupun RBSL tidak efisien untuk digunakan karena peneliti sulit mengontrol kehomogenan petak percobaan dengan kelompok besar, dan sulitnya mengontrol galat percobaan. Percobaan tersebut hanya dapat dianalisis dengan Rancangan Kelompok Tidak Lengkap (RKTL) yang salah satunya adalah Rancangan Lattice Seimbang (RLS).

Adapun model linier aditif dari RLS (Hinkelman & Kempthorn, [6]) adalah:

Yq = μ ^{+ β}j ⁺ Y ⁺ T ^{+ ε}q       ⁽¹⁾

dengan:

^Yijq   ⁼ respon ulangan ke- i , kelompok

ke- j dan perlakuan ke-q

^μ    =   rata-rata data keseluruhan

β.   =  pengaruh ulangan ke- i

γ    =  pengaruh acak pada ulangan ke- i

dan kelompok ke- j

τ    =  pengaruh perlakuan ke- q;

ε = galat percobaan pada ulangan ke-^q       i , kelompok ke- j dan perlakuan

ke- q

Metode yates merupakan metode untuk analisis data hilang pada rancangan percobaan dengan cara menyisipkan nilai dugaan yang meminimumkan JKG. Misalkan suatu percobaan dengan sampel pengamatan dan adalah sebuah data yang hilang pada ulangan ke- , perlakuan ke-b , dan kelompok terkoreksi ke-c, nilai duga P dirumuskan ( Steel & Torrie, [10]):

^ J r × Ra +1 × Tb - D y

{    (t —1)( r — 1)    )

(2)

dengan:

_Pˆ    =  nilai duga data hilang

r   =  banyaknya ulangan

t    =  banyaknya perlakuan

R   =  jumlah nilai ulangan ke- a yang

tidak hilang,

T = jumlah nilai perlakuan ke- b yang tidak hilang

D = jumlah dari data keseluruhan yang tidak hilang

Prosedur pendugaan satu data hilang dengan metode Yates dilakukan dengan menggunakan persamaan (2)

Prosedur pendugaan dua data hilang adalah [5]:

• 1.    Nilai awal dari salah satu data hilang dihitung menggunakan persamaan:

dengan = nilai dugaan awal, = rataan untuk data yang tak hilang pada baris ke- ,

= rataan untuk data yang hilang pada kolom ke- .

• 2.    Nilai dugaan awal yang diperoleh pada langkah 2 digabung dengan data yang tidak hilang. Dengan menggabungkan data yang tidak hilang dan nilai dugaan awal , diduga nilai pengamatan hilang lainnya dengan menggunakan persamaan (2)

• 3.    Selanjutnya dianggap hilang dan diduga kembali dengan menggunakan persamaan (2), langkah 2 dan 3 dilakukan secara bergantian sampai nilai dugaan kedua data konvergen ke suatu nilai tertentu.

Algoritma EM terdiri dari tahap E dan tahap M. Prosedur algoritma EM sebagai penduga data hilang pada RLS ( Dempster, et.al [2]) adalah:

dengan:

^_

μ=

^A—

βi=

^—

γ j=

^T q=

G

Ri

Rij

T

• 1.    Tahap E

Menghitung nilai duga dari parameter yang terdapat pada model linier rancangan (1) dengan metode kuadrat terkecil [7], yaitu:

μ = G, β,= R-G, Y'j= Rj-R_l, ^q = Tq - G      ⁽⁴⁾

nilai duga rata-rata keseluruhan nilai duga parameter pada kelompok ke- j

nilai duga parameter pada ulangan ke- i dan kelompok ke- j

nilai duga parameter pada perlakuan ke- q

nilai rata-rata data

nilai rata-rata ulangan ke- i

nilai rata-rata ulangan ke- i dan kelompok ke- j

nilai rata-rata perlakuan ke- q

• 2.    Tahap M

Substitusi nilai duga parameter yang diperoleh pada tahap E ke dalam model linier RLS (1), agar diperoleh nilai Y yang maksimum [4].

t i + b j x i =------

ij₂

(3)

• 2.    METODE PENELITIAN

• A.    Sumber Data

Data yang dipergunakan dalam penelitian ini adalah data sekunder, yaitu data gabah kering giling (GKG) di Kabupaten Badung tahun 2010 yang terdiri dari 9 perlakuan.

• B.    Desain Simulasi

Pada desain simulasi ini dibahas evaluasi terhadap kedua metode pendugaan data hilang. Untuk itu dilakukan penghilangan data. Penghilangan data dilakukan sampai dua data hilang pada berbagai pola hilang, yaitu dalam satu perlakuan, dalam satu kelompok, dalam satu kolom, dalam satu ulangan dan secara acak.

• C.    Metode Analisis Data

Langkah-langkah analisis dalam penelitian ini adalah:

• 1.    Melakukan      pengacakan      dengan

menggunakan rancangan rencana dasar untuk RLS dan metode bilangan acak, sehingga berdasarkan teori pengacakan diperoleh RLS dengan 9 perlakuan, 4 ulangan, dan 3 kelompok masing-masing ulangan

• 2.    Melakukan analisis ragam dari data lengkap dan data tidak lengkap pada RLS untuk melihat seberapa besar pengaruh dari banyaknya data yang hilang pada RLS.

• 3.    Melakukan pendugaan data hilang dengan langkah-langkah sebagai berikut:

• a.    Melakukan pendugaan data hilang sesuai prosedur pendugaan data hilang dengan Metode Yates

• b.    Melakukan pendugaan data hilang sesuai prosedur algoritma EM

• 4.    Menentukan nilai bias dan ragam dugaan parameter dengan metode Yates dan algoritma EM. Rumus untuk menentukan nilai bias dan ragam parameter dugaan adalah ( Musa, [8]):

Nilai bias parameter dugaan

(5)

Nilai ragam parameter dugaan

₌ ∑λ⅛jo:

(6)

dengan:

= nilai parameter ke

= nilai dugaan parameter ke-=banyaknya    simulasi    sampai

konvergen

• 5.    Melakukan pengujian asumsi-asumsi analisis ragam pada nilai bias dan ragam dugaan parameter

• a.    Pengujian asumsi keaditifan model dengan uji Non Aditivitas Tukey (NAT).

• b.    Pengujian asumsi kenormalan data dengan uji Anderson-Darling.

• c.    Pengujian asumsi kebebasan galat satu dengan lainnya dengan uji Durbin Watson.

• d.    Pengujian asumsi kehomogenan ragam dengan uji Levene

• 6.    Melakukan analisis ragam dari bias dan parameter dugaan menggunakan analisis ragam RAK faktorial dengan model linier (Mattjik & Sumertajaya, [7]).

Yjk = ^{μ +} A ⁺ Dj ⁺ (AD) j ⁺ Pk ^{+ ε}jk

dengan bias dan ragam dugaan parameter sebagai respon, posisi data hilang dan metode pendugaan data hilang sebagai faktor dan parameter sebagai kelompok.

• 7.    Melakukan analisis ragam dari data setelah ditambahkan nilai duga dari data hilang.

• 8.    Melakukan perbandingan hasil analisis ragam data tidak lengkap dengan hasil analisis ragam dari data tidak lengkap ditambahkan nilai duga data hilang. Hal ini untuk melihat seberapa besar perbedaan ketika data hilang tidak diduga dengan data hilang dilakukan pendugaan.

• 3.    HASIL DAN PEMBAHASAN

Data yang digunakan dalam penelitian ini adalah data produksi gabah kering giling (GKG) dalam ton/ha di Kabupaten Badung. Pada data dilakukan pengacakan sesuai teknis pengacakan dan denah pelaksanaan untuk Rancangan Lattice Seimbang (RLS). Data tersebut merupakan data lengkap RLS dengan 9 perlakuan, 4 ulangan dan

• 3 kelompok masing-masing ulangan. Kemudian dari data lengkap tersebut dilakukan penghilangan data pada satu data dan dua data pada satu perlakuan, satu kelompok, satu kolom, satu ulangan, dan secara acak. Data yang memuat data hilang selanjutnya disebut data tidak lengkap.

Sebagai langkah awal berikut ini dilakukananalisis ragam terhadap data lengkap dan data tidak lengkap.

• A.    Analisis Ragam Terhadap Data Lengkap dan Data tidak Lengkap

Analisis ragam terhadap data lengkap dan data tidak lengkap dilakukan untuk melihat pengaruh dari banyaknya data hilang.

Berdasarkan hasil analisis ragam data lengkap dan data tidak lengkap, diberikan nilai JKG seperti tampak pada Tabel 1.

Tabel 1. Nilai JKG Analisis Ragam dari Data Lengkap dan Data Tidak Lengkap

Berdasarkan Tabel 1 tampak bahwa pada saat data lengkap nilai JKG sebesar 11,6409 sedangkan saat terdapat satu data hilang nilai JKG sebesar 27,90802. Hal ini menunjukkan bahwa hilangnya data menyebabkan nilai JKG lebih besar daripada nilai JKG pada analisis ragam data lengkap. Oleh karena itu, dilakukan pendugaan terhadap data hilang tersebut. Pendugaan data hilang dalam penelitian ini menggunakan metode Yates dan algoritma EM.

• B.    Pendugaan Data Hilang dengan Metode
  
  Yates dan Algoritma EM

Metode Yates adalah metode pendugaan data hilang pada rancangan percobaan dengan meminimumkan JKG. Pendugaan satu data hilang dilakukan dengan menggunakan persamaan (2). Untuk pendugaan dua data hilang

pada satu perlakuan, nilai awal x diduga menggunakan persamaan (3), data kedua dihitung menggunakan persamaan (2). Kemudian dugaan awal x yang diperoleh dari persamaan (3) digabung dengan data yang tidak hilang. Dengan menggabungkan data yang tidak hilang dan nilai dugaan awal x , diduga nilai data hilang lainnya dengan menggunakan persamaan(2). Selanjutnya x dianggap hilang dan diduga kembali dengan menggunakan persamaan (2). Langkah tersebut dilakukan secara bergantian sampai nilai dugaan kedua data konvergen ke suatu nilai.

Pendugaan data hilang untuk satu data hilang dengan algoritma EM melalui dua tahap yaitu tahap E dengan menggunakan persamaan (4) dan tahap M dengan menggunakan persamaan (1). Untuk dua data hilang, proses pendugaan dengan algoritma EM, nilai awal diperoleh dari persamaan (4) dan (1). Kemudian, nilai awal tersebut digabung dengan data yang tidak hilang dan data hilang lainnya diduga dengan persamaan (4) dan (1). Selanjutnya nilai awal dianggap hilang dan diduga kembali dengan rumus yang sama. Langkah ini dilakukan secara bergantian sampai nilai dugaan kedua data konvergen ke suatu nilai.

Hasil pendugaan nilai data hilang seperti tampak pada Tabel 2.

Tabel 2. Nilai Duga Data Hilang dan Data Aslinya.

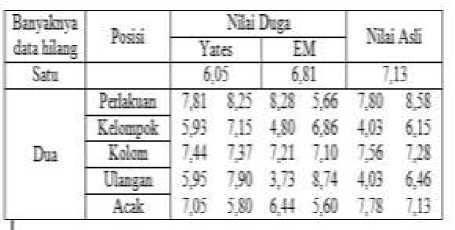
Berdasarkan data yang memuat data hilang ditambahkan data duga pada Tabel 2, dengan persamaan (4), dihitung nilai duga parameter μ, β_i (i = 1,2,3,4), τ_q (q = 1,2,...,9) da n γ_j (i = 1,2,3,4; j = 1,2,3). Selanjutnya

dilakukan perhitungan untuk nilai bias dan ragam dari dugaan parameter dengan menggunakan persamaan (5) dan (6).

Setelah dilakukan pendugaan nilai data hilang dan diperoleh nilai bias dan ragam dugaan setiap parameter, kemudian dilanjutkan dengan melakukan pengujian asumsi analisis ragam terhadap nilai bias dan ragam dugaan parameter.

• C.    Pengujian Asumsi Analisis Ragam Terhadap Bias dan Ragam Parameter Dugaan

Proses pengujian asumsi analisis ragam terhadap bias dan ragam parameter dugaan dilakukan untuk mengetahui apakah nilai bias dan ragam parameter dugaan telah memenuhi asumsi-asumsi dasar untuk dilakukan proses analisis ragam. Adapun asumsi yang harus dipenuhi adalah keaditifan model, kenormalan data, kebebasan galat dan kehomogenan ragam.

• 1.    Pengujian Asumsi Keaditifan Model

Pengujian asumsi     keaditifan model

dilakukan dengan uji Non-Aditivitas Tukey. Pada uji Non-Aditivitas Tukey, aditif ^aPabi^laFhitung ≤ F(_a^db galat). Statistik j NAT untuk nilai bias menghasilkan

Fhitung =0,00416 F_tabel= 3,88312. Oleh karena nilai Fhitung ≤ F        '.ar..0 <>04∣6 < 3,88312,

berarti pengaruh utama perlakuan dan kelompok untuk nilai bias dugaan parameter bersifat aditif pada taraf nyata 5%.Dengan cara yang sama Uji NAT untuk nilai ragam menghasilkan Fhitung= 0,06016 dan F_tabel = 3,90023. Oleh karena nilai Fhitung ≤ F(0,05;i;i60) yaitu0,06016 < 3.90023, berarti pengaruh utama perlakuan dan kelompok untuk nilai ragam dugaan parameter bersifat aditif pada taraf nyata 5%.

• 2.    Pengujian Asumsi Kenormalan Data

Pengujian asumsi kenormalan data dilakukan uji Anderson-Darling. Hasil uji Anderson-Darling untuk nilai bias dan ragam parameter dugaan dengan bantuan minitab 16

berturut-turut tampak pada Gambar 1 dan Gambar 2.

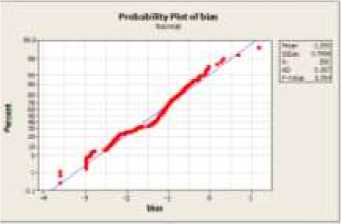
Gambar 1. Uji Normalitas Nilai Bias

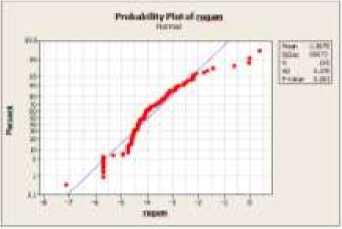
Gambar 2. Uji Normalitas Nilai Ragam

Berdasarkan Gambar 1 dan Gambar 2 terlihat bahwa nilai P uji Anderson-Darling untuk bias dan ragam parameter dugaan secara berturut-turut sebesar 0,764 dan0,263, yang keduanyalebih besar dari α = 0,05 berarti nilai bias dan ragam parameter dugaan mengikuti sebaran normal.

• 3.    Pengujian Kebebasan Galat Percobaan

Pengujian kebebasan galat percobaan dilakukan dengan uji Durbin Watson. Perhitungan uji Durbin Watson untuk nilai bias parameter dugaan menggunakan rumus: n ∑ (ei- ei-1)² d = i=²---------- n ∑ e i =1

Dari sini diperoleh d = 1,937583.Hasil uji

Durbin Watson untuk bias parameter dugaan 1,937583 > d_L = 1,77344 Karena nilai d > d_L berarti tidak terdapat korelasi antargalat pada nilai bias parameter dugaan.

Dengan cara yang sama nilai Durbin Watson dari ragam parameter dugaan diperoleh sebesar 1,999657 > d_L = 1,77344 . Karena nilai d > d_L berarti tidak terdapat korelasi antargalat dari ragam parameter dugaan.

• 4.    Pengujian Kehomogenan Ragam

Pengujian untuk melihat kehomogenan ragam dilakukan dengan uji Levene. Hasil dari uji Levene dengan bantuan program minitab 16 untuk nilai bias dan ragam parameter dugaan secara berturut-turut diberikan pada Gambar 3 dan Gambar 4.

Test for Equal Variances for bias

metode

1

2

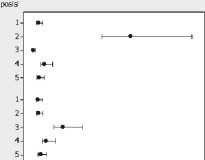
Bartlett's Test

Test Statistic     539.19

P-Value          0.000

Levene's Test

Test Statistic       0.72

P-Value          0.690

95% Bonferroni Confidence Intervals for StDevs

Gambar 3. Uji Kehomogenan Ragam untuk Nilai Bias Parameter Dugaan

Test for Equal Variances for ragam

Bartlett's Test

Test Statistic     1321.06

P-Value          0.000

Levene's Test

Test Statistic         0.79

P-Value          0.621

0.0  0.1   0.2  0.3   0.4   0.5  0.6   0.7  0.8

95% Bonferroni Confidence Intervals for StDevs

Gambar 4. Uji Kehomogenan Ragam dari Ragam Parameter Dugaan

Pada Gambar 3 dan Gambar 4, tampak bahwa P-value untuk uji Levene secara berturut-turut sebesar 0,690 dan 0,621, yang keduanya lebih besar dari α = 0,05 berarti bahwa nilai bias dan ragam parameter dugaan memiliki kehomogenan ragam.

Karena nilai bias dan ragam parameter dugaan memenuhi asumsi-asumsi dasar untuk dilakukan proses analisis ragam, maka selanjutnya dilakukan analisis ragam terhadap bias dan ragam parameter dugaan.

• D.    Analisis Ragam Terhadap Nilai Bias dan
  
  Ragam Parameter Dugaan

Pengujian analisis ragam terhadap bias dan ragam parameter dugaan dilakukan dengan menggunakan analisis ragam RAK faktorial dengan model linier [7].

Yabc ^- P + E_a + H_b + (EH)_ab + p_c + ε_abc

dengan Yabc adalah nilai bias dan ragam dengan data hilang pada posisi a , metode b pendugaan data hilang, dan parameter c , E_a adalah pengaruh data hilang pada posisi a , ^b adalah pengaruh metode b pendugaan data hilang, (EH)_ab adalah pengaruh interaksi antara data hilang pada posisi a dan metode b pendugaan data hilang, dan Pc adalah pengaruh parameter c serta ^£abc adalah pengaruh galat dengan data hilang pada posisi a , metode b pendugaan data hilang, dan parameter c, Dalam hal ini a = satu perlakuan, satu kelompok, satu kolom, satu ulangan dan acak, b = metode Yates, algoritma EM, serta c=µ,β₁,β₂,β₃,β₄,γ₁₁,γ₁₂,γ₁₃,

γ₂₁,γ₂₂,γ₂₃,γ₃₁,γ₃₂,γ₃₃,γ₄₁,γ₄₂,γ₄₃,τ₁ ,τ₂ ,τ₃ ,τ₄,τ₅,τ₆,τ₇ ,τ₈,τ₉.

Pengujian analisis ragam terhadap bias dan ragam parameter dugaan dilakukan untuk melihat pengaruh metode dan posisi data hilang terhadap bias dan ragam dugaan parameter. Oleh karena itu hipotesis untuk uji analisis ragamnya adalah:

• a.    H : Pendugaan parameter tidak berpengaruh nyata terhadap respon

H   :  Parameter   berpengaruh   nyata

terhadap respon

• b.    H   :  Posisi tidak berpengaruh nyata

terhadap respon

H : Posisi berpengaruh nyata terhadap respon

• c.    H : Metode tidak berpengaruh nyata terhadap respon

H : Metode berpengaruh nyata terhadap respon

• d.    H : Interaksi posisi dengan metode tidak berpengaruh nyata terhadap respon

H : Interaksi posisi dengan metode berpengaruh nyata terhadap respon

Hasil analisis ragam untuk bias dan ragam parameter dugaan dengan bantuan program minitab 16 secara berturut-turut tampak pada Tabel 3 dan Tabel 4.

Tabel 3. Hasil Analisis Ragam Terhadap Bias Parameter Dugaan

Sumbei	EF	Iik	KT			a	I KeptEUiaii
Paianeier	25	38,9604	15584	2,91	O1OOO	0,05	g, d⅛>lak
Posisi	4	Wl	1,17”	2,19	0,007	0,05	g. ditolak
Metode	1	0.2823	02823	053	0.469	0,05	H- dllδfi∏U
PosisitMaote	4	0,9550	02387	0,45	0,776	0,05	H.teani
Enw	225	120,6819	0,5364
Total	259	165588'

Tabel 4. Hasil Analisis Ragam Terhadap Ragam Parameter Dugaan

Saater	EF	X	KI	F=	P	a SStSSE
⅛3ΞE5<		85 4663	35436	6.03	OOOO	005 J,	&£k
Jmsi	4	9O5~	10938	156	OJM	0.05 £	ditolak
Metote	1	0,4210	OJOE	GOO	0964	0.05 3	c≥≡s
PassrtXfetote	4	111**5	1'944	4*6	OOOl	0.05 B	ditolak
⅛≡	IM	9399λ5	056*5
Toal	194	199.71«

Berdasarkan Tabel 3 dan Tabel 4 tampak bahwa parameter dan posisi memiliki p - value < α .Oleh karena itu H0 ditolak, yang berarti pendugaan parameter dan posisi data hilang berpengaruh nyata pada taraf 0,05 terhadap nilai bias dan ragam parameter dugaan. Hal ini menunjukkan bahwa ketika hasil pendugaan parameter berbeda maka terdapat perbedaan nilai bias dan ragam dari masing-masing parameter dugaan, demikian juga ketika posisi data hilang berbeda maka terdapat perbedaan nilai bias dan ragam parameter dugaan dari masing-masing posisi data hilang.

Pada Tabel 4 tampak juga untuk interaksi antara posisi dengan metode dengan p — value = 0,01 < α = 0,05 sehingga H₀ ditolak, yang berarti interaksi antara posisi data hilang dengan metode pendugaan data hilang berpengaruh nyata pada taraf 0,05 terhadap ragam dari parameter dugaan. Hal ini menunjukkan ketika terjadi interaksi antara posisi data hilang dengan metode pendugaan data hilang maka terdapat perbedaan ragam parameter dugaan ketika metodenya berbeda atau posisinya yang berbeda.

Selanjutnya dilakukan perbandingan untuk melihat metode mana yang lebih baik di antara dua metode yang dipergunakan. Metode

dikatakan lebih baik apabila memiliki nilai bias dan ragam terkecil. Rata-rata nilai bias dan ragam dari nilai duga dan parameter dugaan berturut-turut diberikan pada Tabel 5 dan Tabel 6.

Tabel 5. Bias dan Ragam dari Nilai Duga

Bar-Tisvi	Psss	BtssNEsIkn		Ξj2ΞS VlZ DtXx
		Yzes	EM	IES	EM
Ssa		1,08167	022371	L1SI82	0,10585
	Sas	116953	IJKW	C 22304	4,42193
	Sas	1,45651	0,74727	⅛76∣5I	4,36448
Dta	Sas KoSfflE	0,10111	0,26320	0,01124	0,16793
	Szn l2≡E≤3Π.	1,04®	1,28353	192450	2,66750
	Acafc	LJBCM	1,43483	L1M⅛	ICtMdS

Tabel 6. Bias dan Ragam dari Parameter Dugaan

Bariiziya ⅛ Irigff	Poas	BzsNaE Ouga	BaazuNEaiDma
		Tres j EM	Yaie j EM
Syn		0.25762    0 22'65    BlMOlI    B00O14 0,10938   ILllMC   BJBiB    0,03646 0,65083    0,19054    0,09173    0,00081 0,07922    0,28058    IL0∞10     0,0092! 0,20165    OJiSJS    BOGlM    0,00096 0,14885    0,14972    0,00078    0,00097
Dna	Sxn Priairren Sxn Kelccrok Sxn Kaiani Sxn jΛ2∑≤2n Ask

Berdasarkan Tabel 5 dan Tabel 6 tampak bahwa pendugaan data hilang pada saat terdapat satu data hilang dengan algoritma EM lebih baik daripada metode Yates karena rata-rata nilai bias dan ragam dari nilai duga dan parameter dugaan untuk algoritma EM lebih kecil dari metode Yates.

Dengan demikian metode Yates untuk dua data hilang cenderung lebih baik digunakan pada posisi data hilang pada satu perlakuan, satu kolom dan secara acak. Algoritma EM untuk dua data hilang cenderung lebih baik digunakan pada saat terdapat satu data hilang dan pada posisi data hilang dalam satu kelompok dan ulangan.

Setelah diketahui metode yang lebih baik dalam pendugaan nilai data hilang berdasarkan posisi data hilangnya, kemudian dilakukan analisis ragam terhadap data yang memuat data hilang dan ditambah dengan nilai duga data hilang.Selanjutnya dilakukan pernbandingan hasil untuk nilai JKG antara data tidak lengkap dengan data tidak lengkap yang ditambahkan nilai duga.

• E.    Perbandingan Hasil Nilai JKG dari Data Tidak Lengkap dengan Data Tidak Lengkap Setelah Ditambah Nilai Duga Data Hilang

Sebelumnya telah dilakukan analisis ragam dari data tidak lengkap. Kemudian, untuk melihat seberapa besar perbedaan nilai JKG ketika nilai data hilang tidak dilakukan pendugaan dan nilai data hilang yang dilakukan proses pendugaan, selanjutnya dilakukan analisis ragam terhadap data tidak lengkap dengan ditambahkan nilai duga.

Berdasarkan hasil analisis ragam diberikan nilai JKG dari data tidak lengkap dan data lengkap setelah ditambahkan nilai duga seperti tampak pada Tabel 7.

Tabel 7. Hasil Nilai JKG dari Data Tidak Lengkap dan Data Tidak Lengkap Ditambah Nilai Duga Data Hilang.

Banvaknva. ⅛Γ* Ii* 13∏p	Posta	Hasil Nilai JKG Sebelum Diduga	HaaL Nilai JKG Setelah Dtduga		Hastl Nilat JKG dan Data Leoskap
			Yates	EM
Satu	-	2 7.90 30     10.8 713   11304 8 563985     IL 6767   15,7437 32,9239      9,6255    10,6682 28,9294     11.5012   11,3159      • 423191     10.7538   14,6987 51,1097     10.9431   11,3876
Dua	Sani Perlakuan Saru KeZcrnpok Saru Kolom Saru Ulansan SaruAcak

Analisis ragam dari data dengan satu data hilang yang belum dilakukan pendugaan data pada Tabel 7 memiliki nilai JKG sebesar 27,9080, sedangkan analisis ragam terhadap data dengan satu data hilang yang telah ditambahkan nilai duga baik diduga dengan metode Yates maupun algoritma EM, memiliki nilai JKG yang lebih kecil dan tidak jauh berbeda dari nilai JKG data lengkap.

Hal yang sama juga berlaku pada analisis ragam dengan dua data hilang yang tidak dilakukan pendugaan data, memiliki nilai JKG lebih besar dibandingkan dengan analisis ragam pada data hilang yang telah ditambahkan nilai duga dan juga nilai JKG dari data hilang setelah ditambah nilai duga tidak jauh berbeda dengan nilai JKG dari data lengkap.

• 4. KESIMPULAN

Berdasarkan analisis dan pembahasan pendugaan data hilang dengan menggunakan metode Yates dan Algoritma EM pada Rancangan Lattice Seimbang maka pendugaan data hilang Metode Yates cenderung lebih baik digunakan pada posisi data hilang dalam satu perlakuan, satu kolom dan secara acak, karena rata-rata nilai bias dan ragamnya lebih kecil. Algoritma EM cenderung lebih baik digunakan pada saat terdapat satu data hilang dan pada saat terdapat dua data hilang pada posisi data hilang dalam satu kelompok dan ulangan.

Hasil analisis ragam dari data dengan data hilang yang tidak dilakukan pendugaan data, memiliki nilai JKG lebih besar dibandingkan dengan analisis ragam dari data dengan ditambahkan nilai data duga dan juga nilai JKG dari data hilang setelah ditambah nilai duga tidak jauh berbeda dengan nilai JKG dari data lengkap, baik dengan metode Yates maupun algoritma EM

DAFTAR PUSTAKA

• [1]    Black, W.J. Anderson, R. Hair, J.J, Babin,

B. & Tatham, R. 2006. Multivariate Data

Analysis. 6th ed. New Jersey: Prentice Hall.

• [2]    Dempster, A.P. Laird, N.M. & Rubin, D.B., 1977. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society.

Series B (Methodological), 39(1), pp.1-38.

• [3]    Fatimah, I. 2003. Data Hilang dalam Rancangan Percobaan (Suatu Kajian Algoritma EM dan Metode Yates). Skripsi. Bogor: IPB Tidak diterbitkan.

• [4]    Goejantoro, R. 2012. Data Tidak Lengkap dan Algoritma Ekspektasi-Maksimisasi. Jurnal Eksponensial, 3( 2), pp.85 - 88.

• [5]    Gomez, K.A. & Gomez, A.A. 1995.

Prosedur Statistik untuk Penelitian Pertanian. 2nd ed. Terjemahan: Sjamsudin, E & J.S Baharsyah. Jakarta: Universitas Indonesia.

• [6]    Hinkelman, K. & O. Kempthorne. 2006.

Design and Analysis of Experiments. 2nd ed. New York.

• [7]    Mattjik, A.A. & Sumertajaya, I.M. 1999. Analisis Perancangan Percobaan Dengan Aplikasi SAS dan Minitab. 1st ed. Bogor: IPB Press.

• [8]    Musa, M.S. 1998. Memahami Statistika Sebagai Alat untuk Penelitian : Rancangan Kajian. 1st ed. Bogor: Jurusan Statistika IPB.

• [9]    Sriliana, I. 2013. Penduga Data Hilang Pada Rancangan Bujur Sangkar Latin Dasar. Kumpulan Makalah Seminar Semirata, F MIPA Universitas Lampung, pp.275-81.

• [10]    Steel, R.G.D. & Torrie, J.H. 1991. Prinsip dan Prosedur Statistika Suatu Pendekatan Biometrik. 2nd ed. Terjemahan: Bambang Sumantri. Jakarta: PT Gramedia Pustaka Utama.

• [11]    Widiharih, T. 2007. Estimasi Data Hilang pada Rancangan Acak Kelompok Lengkap. Jurnal Matematika, 10(2), pp.60-65.

82