INTERPOLASI SPASIAL DENGAN METODE ORDINARY KRIGING MENGGUNAKAN SEMIVARIOGRAM ISOTROPIK PADA DATA SPASIAL (Studi Kasus: Curah Hujan di Kabupaten Karangasem)
on
E-Jurnal Matematika Vol. 4 (1), Januari 2015, pp. 26-30
ISSN: 2303-1751
INTERPOLASI SPASIAL DENGAN METODE ORDINARY KRIGING MENGGUNAKAN SEMIVARIOGRAM ISOTROPIK
PADA DATA SPASIAL
(Studi Kasus: Curah Hujan di Kabupaten Karangasem)
Putu Mirah Purnama D§1, Komang Gde Sukarsa2, Komang Dharmawan3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: mirahpurnamadewi@yahoo.co.id]
2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sukarsakomang@yahoo.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: dharmawan.komang@yahoo.com] §Corresponding Author
ABSTRACT
Spatial data is data that is presented in the geographic of an object, related to the location, shape and relationship of the earth in space. One of example of spatial data is rainfall. To determine the value of rainfall in an area, built to predict rain post information regarding rainfall. Spatial interpolation is used to estimate rainfall by collecting rainfall values held rain heading around. Assessment methods used in the estimate the rainfall in the Karangasem district is ordinary kriging using isotropic semivariogram that takes into account height on spatial data. Isotropic semivariogram which only takes into account the distance alone. Ordinary kriging method using isotropic semivariogram that takes into account height value estimated rainfall is much different to the values at the control points Amlapura and Besakih. Interpolation on 3D data are not suitable for use on ordinary kriging method, grouping should be done at the data into a few weeks to application of ordinary kriging interpolation method using anisotropic semivariogram on 3D data
Keywords: Spatial interpolation, Ordinary Kriging, Isotropic Semivariogram, 3D Data
Data spasial merupakan data yang disajikan dalam posisi geografis dari suatu obyek, berkaitan dengan lokasi, bentuk dan hubungannya dalam ruang bumi (Cressie [3]). Salah satu contoh data spasial adalah hujan. Hujan adalah fenomena jatuhnya air dari awan ke bumi. Pada mulanya air hujan tersebut berasal dari beberapa sumber air yang ada di bumi, seperti misalnya air laut, air sungai, danau, waduk, dan lain sebagainya yang mengandung air. Fenomena hujan merupakan salah satu subjek yang menarik untuk dipelajari karena kelebihan atau kekurangan hujan berpengaruh buruk bagi kehidupan makhluk hidup.
Banyaknya hujan dapat diukur dengan suatu ukuran yang disebut curah hujan. Curah hujan adalah ketinggian air hujan yang terkumpul pada tempat yang datar, tidak
menguap, tidak meresap, dan tidak mengalir (Balai Besar Meteorologi Klimatologi dan Geofisika Wilayah III Denpasar [2]). Untuk mengetahui curah hujan pada suatu daerah, maka pemerintah dibantu oleh Badan Meteorologi Klimatologi dan Geofisika membangun pos hujan di beberapa titik tertentu untuk mengamati dan mengukur curah hujan sebagai informasi yang akan diberikan pada masyarakat.
Nilai curah hujan di daerah sekitar pos-pos hujan tidak diketahui secara pasti karena tidak semua daerah mempunyai pos hujan sendiri. Oleh karena itu diperlukan suatu metode interpolasi untuk menduga nilai curah hujan pada tempat yang tidak memiliki pos hujan dengan cara menghimpun nilai pos-pos hujan yang ada disekitarnya. Karena data curah hujan merupakan suatu data spasial, maka interpolasi
yang digunakan dalam kasus ini adalah interpolasi spasial. Metode penaksiran yang digunakan untuk menduga nilai pada suatu titik disebut dengan metode kriging. Metode kriging yang sesuai untuk menyelesaikan kasus ini adalah ordinary kriging, karena dalam kasus ini digunakan untuk menduga nilai pada lokasi yang datanya tidak tersedia.
Pada penelitian sebelumnya oleh Ayuni [1], meneliti pendugaan nilai curah hujan di suatu titik pada data spasial yang memperlihatkan lintang dan bujur dengan metode Ordinary Kriging dan Inverse Distance Weighted pada data set yang tidak mengandung pencilan. Metode ordinary kriging tersebut menggunakan semivariogram isotropic karena penelitian tersebut hanya bergantung pada jarak saja tanpa memperhitungkan arah. Titik kontrol yang diambil oleh penelitian sebelumnya adalah titik kontrol Amlapura dan Besakih. Selanjutnya pada penelitian Suma [4] menggunakan data yang sama dengan peneliti sebelumnya meneliti pendugaan nilai curah hujan di suatu titik pada data spasial yang memperlihatkan lintang dan bujur dengan menggunakan metode Ordinary Kriging dan Robust Kriging. Metode ordinary kriging tersebut menggunakan semivariogram isotropik. Kedua penelitian tersebut sama-sama mengidentifikasi ada atau tidaknya pencilan dari data tersebut. Digunakannya Robust Kriging karena penelitian tersebut menyertakan data pencilan untuk menduga nilai curah hujan pada suatu titik.
Pada penelitian ini, penulis tertarik untuk meneliti bagaimana pendugaan nilai curah hujan di suatu titik pada data spasial dengan menambahkan data ketinggian pos hujan dari permukaan laut pada data sebelumnya yang memengaruhi curah hujan pada suatu titik data spasial. Metode yang akan penulis gunakan adalah metode ordinary kriging menggunakan semivariogram isotropik yang memperhitungkan ketinggian. Menurut penulis, pengaruh ketingian yaitu ketinggian tempat dari permukaan laut merupakan faktor penting dalam pendugaan nilai curah hujan pada suatu titik karena semakin tinggi suatu tempat maka semakin sering terjadi hujan karena mengingat
proses terjadinya hujan yaitu bermula dari air laut, danau dan sungai yang terkena panas, lalu terjadi penguapan diatas menjadi uap air yang terkondensasi menjadi awan, setelah diatas tergantung pergerakan dari arah mata angin misalnya pergerakan angin dari dataran rendah menuju dataran tinggi. Maka dari itu ketinggian suatu tempat dari permukaan laut memengaruhi hujan.
Ordinary Kriging
Ordinary Kriging mengasumsikan mean populasi konstan, tetapi tidak diketahui dan variogram dari Z(x) diketahui. Metode ini merupakan metode yang memberikan penaksir linear tak bias terbaik (best linear unbiased estimator (BLUE)).
Bobot ordinary kriging memenuhi sifat tak bias dengan ∑i=l λ1 =1 dengan n adalah jumlah sampel yang diketahui. Nilai bobot ordinary kriging dapat diperoleh melalui persamaan berikut (Oliver and Webster [7]):

Parameter tambahan µ adalah Langrange multiplier yang digunakan untuk meminimalkan galat kriging. Interpolasi ordinary kriging dapat diperoleh dengan persamaan berikut:
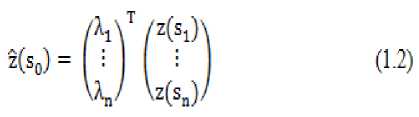
dan variansi galat kriging dapat diperoleh dari persamaan:
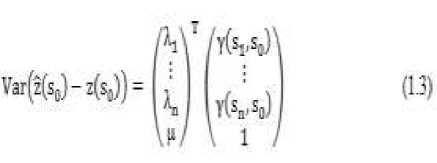
Keterangan :
sQ : titik atau lokasi yang akan diduga
s1,s2,…,sn : titik atau lokasi sampel yang diketahui nilainya
λ 1 ,λ2,…,λn : bobot tiap lokasi tersampel γ(si,sj ) : semivariogram titik s 1 dan s 2
γ(si,sQ ) : semivariogram titik s 1 dengan
titik yang akan diduga
µ : Langrange multiplier
ẑ(sQ ) : nilai dugaan pada titik yang akan
diduga
z(s I ) : nilai pada titik tersampel
s1 sebagai model isotropik eqivalen, γ(h1) (Widhita [5])
Data yang digunakan adalah data sekunder yang diperoleh secara tidak langsung atau data yang dikumpulkan oleh pihak lain. Dalam hal ini data diperoleh pada penelitian sebelumnya oleh Ayuni [1] serta ditambahkan kembali oleh penulis dengan mengambil data lain yang masih bersangkutan dengan penelitian. Data tersebut telah dikumpulkan oleh Badan Meteorologi Klimatologi dan Geofisika Wilayah III Denpasar. Data yang dimaksud adalah data curah hujan bulanan tahun 2009 pada seluruh pos hujan di Kabupaten Karangasem
Populasi dalam penelitian ini adalah seluruh daerah dan pos hujan di Kabupaten Karangasem dan yang menjadi sampel adalah pos hujan Amlapura dan Besakih yang dipilih secara purpossive dimana pos hujan yang menjadi sampel memiliki nilai amatan yang bukan merupakan data pencilan
Tahap-tahap analisis data penelitian, melalui tahapan berikut: Memeriksa plot data sampel yang tidak mengandung pencilan yang telah dilakukan sebelumnya; Memeriksa asumsi stationer orde dua pada masing-masing data set curah hujan; Menentukan model
semivariogram; Fungsi yang dipilih sebagai model semivariogram adalah adalah model Gaussian; Pengujian model semivariogram dengan menggunakan validasi silang; Pemilihan model semivariogram yang terbaik berdasarkan pengujian validasi silang; Menghitung nilai bobot masing-masing titik amatan terhadap titik kontrol dengan model semivariogram terbaik; Mencari nilai dugaan pada titik kontrol menggunakan bobot masing-masing titik amatan yang diperoleh dari model
semivariogram terbaik; Melakukan langkah tiga sampai delapan untuk set data curah hujan yang bukan merupakan pencilan; Menghitung nilai root mean square error (RMSE) dari metode ordinary kriging menggunakan semivariogram isotropik yang memperhitungkan ketinggian pada data spasial.
-
3. HASIL DAN PEMBAHASAN
Perbandingan Nilai Dugaan Titik Kontrol dengan Nilai Amatan
Nilai dugaan yang diperoleh dari interpolasi dengan metode Ordinary Kriging ini selanjutnya dibandingkan dengan nilai amatan sebenarnya. Selisih nilai tersebut nantinya akan digunakan dalam perhitungan untuk mendapatkan tingkat kesalahan (error).
Tabel 1. Nilai Amatan dan Nilai Dugaan Titik Kontrol Amlapura dengan Metode Ordinary Kriging
|
Data Set |
Nilai Amatan |
Nilai Dugaan |
Kuadrat Galat |
|
Februari |
542 |
168,1585 |
139757,4671 |
|
Maret |
63 |
0 |
0 |
|
April |
111 |
0 |
12321 |
|
Mei |
161 |
155,1797 |
33,8759 |
|
Juni |
14 |
18,24736 |
18,0404 |
|
Juli |
49 |
104,7515 |
3108,2297 |
|
September |
58 |
815,628 |
529442,5063 |
|
Desember |
90 |
13,3285 |
5873,9195 |
Tabel 2. Nilai Amatan dan Nilai Dugaan Titik Kontrol Besakih dengan Metode Ordinary Kriging.
|
Data Set |
Nilai Amatan |
Nilai Dugaan |
Kuadrat Galat |
|
Februari |
560 |
370,6085 |
35869,1402 |
|
Maret |
194 |
0 |
0 |
|
April |
200 |
180,485 |
380,8352 |
|
Mei |
223 |
144,3919 |
6179,2333 |
|
Juni |
46 |
10,48695 |
1261,2015 |
|
Juli |
73 |
107,7345 |
1206,4854 |
|
September |
241 |
85,6755 |
24125,7003 |
|
Desember |
339 |
225,6959 |
12837,8190 |
Setelah mendapatkan nilai dugaan pada kedua titik amatan tersebut, selanjutnya nilai dugaan tersebut akan dibandingkan dengan nilai dugaan dari penelitian sebelumnya
Berikut ini perbandingan nilai dugaan masing-masing titik kontrol penelitian dengan metode ordinary kriging menggunakan semivariogram isotropik yang tidak memperhitungkan ketinggian dan metode ordinary kriging menggunakan semivariogram isotropik yang memperhitungkan ketinggian
Tabel 3. Nilai Dugaan dengan Metode Ordinary
Kriging Menggunakan Semivariogram Isotropik yang tidak memperhitungkan ketinggian dan yang memperhitungkan ketinggian pada Titik Kontrol Amlapura
|
Data Set |
Metode Ordinary Kriging | |
|
Tanpa Ketinggian |
Dengan Ketinggian | |
|
Nilai dugaan |
Nilai Dugaan | |
|
Februari |
415,9845 |
168,1585 |
|
Maret |
85,6779 |
0 |
|
April |
175,7113 |
0 |
|
Mei |
104,4944 |
155,1797 |
|
Juni |
17,6089 |
18,24736 |
|
Juli |
27,9975 |
104,7515 |
|
September |
74,2771 |
815,628 |
|
Desember |
219,6254 |
13,3285 |
Tabel 4. Nilai Dugaan dengan Metode Ordinary Kriging menggunakan semivariogram isotropik yang tidak memperhitungkan ketinggian dan yang memperhitungkan ketinggian pada Titik Kontrol Besakih
|
Data Set |
Metode Ordinary Kriging | |
|
Tanpa Ketinggian |
Dengan Ketinggian | |
|
Nilai dugaan |
Nilai dugaan | |
|
Februari |
383,6051 |
370,6085 |
|
Maret |
91,0137 |
0 |
|
April |
191,9792 |
180,485 |
|
Mei |
166,1806 |
144,3919 |
|
Juni |
9,3069 |
10,48695 |
|
Juli |
72,9694 |
107,7345 |
|
September |
230,5143 |
85,6755 |
|
Desember |
251,8545 |
225,6959 |
Berdasarkan perbandingan nilai dugaan pada tabel 3 dan tabel 4 di atas terlihat bahwa hasil dari dugaan nilai curah hujan dengan titik
control Amlapura dan Besakih dengan metode ordinary kriging menggunakan semivarigram isotropik yang memperhitungkan ketinggian memperoleh nilai dugaan yang sangat jauh berbeda dengan hasil dugaan yang dilakukan oleh penelitian sebelumnya, terlihat pada hasil dugaan penelitian ini ada nilai amatan yang tidak bisa diduga yaitu bulan maret dan nilai dugaan curah hujan lainnya sangat jauh berbeda pada data asli.
Berdasarkan hasil diskusi pada sistem geografi informasi MIT menyatakan bahwa interpolasi untuk data 3D tidak dapat digunakan pada metode ordinary kriging, sebaiknya dilakukanlah pengkelompokan pada variable bebas menjadi beberapa bagian pada R untuk penerapan interpolasi dengan metode ordinary kriging menggunakan semivariogram isotropik pada data 3D. Hasil analisis ini jauh berbeda dari hasil penelitian sebelumnya, perbedaan ini berdasarkan hasil diskusi Whuber dan emDiaz [6] karena penelitian ini tidak dilakukan pengelompokan data berdasarkan kelas.
RMSE (Root Mean Square Error) merupakan suatu besaran kesalahan yang digunakan untuk membandingkan ketelitian dari metode ordinary kriging. Root Mean Square Error dihitung pada saat dua, tiga, empat kali dan seterusnya hingga delapan kali interpolasi. Karena nilai dugaan curah hujan dengan menggunakan metode ordinary kriging menggunakan semivariogram isotropik yang memperhitungkan ketinggian menghasilkan dugaan yang jauh dari nilai amatan dan dari penelitian sebelumnya, sehingga disimpulkan metode yang digunakan penulis untuk menduga nilai curah hujan dengan data yang sama dengan penelitian Ayuni [1] kurang baik dan tidak dilanjutkan ke tahap penentuan RMSE
Kesimpulan
Dari penelitian yang dilakukan dapat ditarik beberapa kesimpulan yaitu metode Ordinary Kriging menggunakan semivariogram isotropik yang memperhitungkan ketinggian memberikan nilai pendugaan curah hujan yang jauh berbeda
terhadap nilai pada titik kontrol Amlapura dan Besakih dan Ketinggian memengaruhi dalam pendugaan nilai curah hujan pada suatu titik
Saran
Metode Kriging yang digunakan dalam penelitian ini adalah metode Kriging dengan semivariogram isotropik yang memperhitungkan ketinggian dengan tidak mengkelompokan data berdasarkan kelas sehingga untuk penelitian lebih lanjut dapat dikembangkan dengan menggunakan semivariogram anisotropik dengan mengkelompokan data menjadi beberapa kelas. Selain itu dapat digunakan jenis Kriging lain seperti Co-Kriging yang merupakan suatu teknik khusus dalam interpolasi dengan memakai dua variabel yang berbeda akan tetapi secara spasial saling berhubungan maupun Universal Kriging yang merupakan Kriging untuk data yang mempunyai kecenderungan trend tertentu.
Anisotropik”. Skripsi. Departemen
Matematika, FMIPA Universitas
Indonesia. Tidak diterbitkan.
-
[6] Whuber dan emDiaz. 2013. Ordinary Kriging with Three Dimension in R. http://gis.stackexchange.com. Diakses 16 agustus 2014
-
[7] Oliver, M. A and R. Webster 2007. Geostatistic for Environmental Statistic. Second Edition. United Kingdom: Willey
DAFTAR PUSTAKA
-
[1] Ayuni, Ni Wayan Dewinta. 2011. “Perbandingan Metode Ordinary Kriging dan Inverse Distance Weighted (IDW) pada Interpolasi Spasial (Studi Kasus: Curah Hujan di Kabupaten Karangasem)”. Skripsi. Jurusan Matematika FMIPA
Universitas Udayana. Bukit Jimbaran. Tidak di terbitkan.
-
[2] Balai Besar Meteorologi Klimatologi dan
Geofisika Wilayah III Denpasar.2012. “Informasi Cuaca, Iklim, dan Gempabumi Provinsi Bali”. Buletin Meteorologi Klimatologi dan Geofisika Tahun VI No. 09.
-
[3] Cressie, N.1993. Statistic for Spatial Data. Revised Edition. New York : Willey.
-
[4] Suma Fridayani, Ni Made. 2012.
“Perbandingan Interpolasi Spasial dengan Metode Ordinary dan Robust Kriging pada Data Berpencilan”. Skripsi. Jurusan Matematika FMIPA Universitas Udayana. Bukit Jimbaran. Tidak diterbitkan.
-
[5] Widhita, Putu Jaya Adnyana. 2008. “Penaksiran Kandungan Cadangan Bauksit di Daerah Mepawah Menggunakan Ordinary Kriging dengan Semivariogram
30
Discussion and feedback