MENGATASI HETEROSKEDASTISITAS PADA REGRESI DENGAN MENGGUNAKAN WEIGHTED LEAST SQUARE

E-Jurnal Matematika Vol. 4 (1), Januari 2015, pp. 20-25

ISSN: 2303-1751

MENGATASI HETEROSKEDASTISITAS PADA

REGRESI DENGAN MENGGUNAKAN WEIGHTED LEAST SQUARE

Putu Ayu Maziyya^§1, I Komang Gde Sukarsa², Ni Made Asih³

¹Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

²Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

³Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] ^§Corresponding Author

ABSTRACT

In the regression analysis we need a method to estimate parameters to fulfill the BLUE characteristic. There are assumptions that must be fulfilled homoscedasticity one of which is a condition in which the assumption of error variance is constant (same), infraction from the assumptions homoskedasticity called heteroscedasticity. The Consequence of going heteroscedasticity can impact OLS estimators still fulfill the requirements of not biased, but the variant obtained becomes inefficient. So we need a method to solve these problems either by Weighted Least Square (WLS). The purpose of this study is to find out how to overcome heteroscedasticity in regression with WLS. Step of this research was do with the OLS analysis, then testing to see whether there heteroscedasticity problem with BPG method, the next step is to repair the beginning model by way of weighting the data an exact multiplier factor, then re-using the OLS procedure to the data that have been weighted, the last stage is back with a heteroscedasticity test BPG method, so we obtained the model fulfill the assumptions of homoskedasicity. Estimates indicate that the WLS method can resolve the heteroscedasticity, with exact weighting factors based on the distribution pattern of data seen.

Keywords: heteroscedasticity, OLS, WLS

• 1.    Pendahuluan

Dalam analisis regresi diperlukan suatu metode untuk menduga parameter agar memenuhi sifat BLUE (Best Linear Unbiased Estimator), salah satu metode yang paling sering digunakan adalah Ordinary Least Square (OLS) atau sering disebut dengan Metode Kuadrat Terkecil (MKT). Salah satu asumsi klasik yang harus dipenuhi dalam estimasi OLS agar hasil estimasinya dapat diandalkan, yaitu ragam sisaan homogen E (u ²) = σ² (homoskedasti-sitas). Pelanggaran terhadap asumsi homoskedastisitas disebut heteroskedastisitas, yang artinya galat bersifat tidak konstan. Konsekuensi dari terjadi heteroskedastisitas dapat mengakibatkan penduga OLS yang diperoleh tetap memenuhi persyaratan tak bias, tetapi varian yang diperoleh menjadi tidak efisien, artinya varian cenderung membesar

sehingga tidak lagi merupakan varian yang kecil. Dengan demikian model perlu diperbaiki dulu agar pengaruh dari heteroskedastisitas hilang (Gujarati [3]).

Mengingat secara statistik permasalahan heteroskedastisitas tersebut dapat mengganggu model yang akan diestimasi, bahkan dapat menyesatkan kesimpulan yang diambil maka diperlukan metode untuk mengatasi masalah tersebut. Metode Weighted Least Square (WLS) merupakan metode alternatif yang dapat mengatasi heteroskedastisitas. Metode WLS sama halnya seperti metode OLS dengan meminimumkan jumlah sisaan hanya saja pada metode WLS dilakukan pembobotan suatu faktor yang tepat kemudian baru menggunakan metode OLS terhadap data yang telah diboboti.

Metode WLS memiliki keunggulan dibandingkan dengan OLS yaitu metode WLS bisa mengatur pentingnya setiap observasi

karena pada OLS diasumsikan bahwa nilai duga parameter regresi bernilai sama untuk setiap observasi. Mekanisme kerja WLS yaitu apabila varian variabel gangguan tidak diketahui maka untuk menyelesaikan masalah heteroskedasti-sitas adalah dengan mengetahui pola heteroskedastisitas itu sendiri, jika variabel gangguan proporsional terhadap X_i maka model akan dibagi dengan √X, jika varian variabel gangguan adalah proporsional terhadap X_i sehingga model akan dibagi dengan , selain proporsional dengan     dan      bisa juga

diasumsikan bahwa pola varian variabel gangguan adalah proporsional terhadap [E(Y_i]]² sehingga dibagi dengan E (Y_i] (Gujarati [3]).

Pada penelitian ini penulis ingin mengetahui bagaimana cara mengatasi heteroskedastisitas pada regresi dengan metode Weighted Least Square. Pada penelitian ini digunakan data yang mengandung masalah heteroskedastisitas.

• 1.1    Metode Kuadrat Terkecil

Model persamaan regresi linier berganda: ^Yi ^{x β}0 ⁺ β∖1∖ i + ^β2 ^X2 i +----⁺ βk^xk i + ^εi  ^[1]

Metode kuadrat terkecil adalah metode yang bertujuan untuk meminimumkan jumlah kuadrat galat (sum square error). Pendugaan koefisien regresi linear berganda dengan metode kuadrat terkecil dapat dilakukan dengan menggunakan persamaan matriks [4], sebagai berikut:

b = (X^τX]- ¹X^tY

• 1.2    Weighted Least Square

Pada estimasi OLS, salah satu asumsi yang harus dipenuhi adalah

E { εε'} = σ ²

yaitu galat bersifat homoskedastisitas. Greene [1] menyatakan apabila terjadi pelanggaran asumsi tersebut, yakni kemungkinan variansinya tidak sama (heteroskedastisitas), maka metode yang dapat digunakan untuk menduga koefisien regresi adalah metode Generalized Least Square (GLS). Penaksir β pada metode GLS diperoleh dengan cara mentransformasikan model regresi

linier terlebih dahulu sehingga dapat memenuhi asumsi-asumsi pada OLS.

Asumsi yang diberikan pada metode GLS adalah: E{ε} = 0 dan E{ετ^τ} = σ² Ω Dengan Ω merupakan matriks simetrik definit positif dan nonsingular yang diketahui dan berukuran n x n, sehingga Ω dapat difaktorisasi menjadi:

Ω = CΛ C^t

Dengan C merupakan matriks dengan kolom-kolomnya adalah vektor ciri dari Ω dan Λ merupakan matriks diagonal dengan unsur diagonalnya akar ciri dari Ω.

Didefinisikan variabel baru T = ΛΛ ¹ /² dengan Λ ^1/2 merupakan matriks diagonal yang entri pada diagonal ke-i adalah √λ_t sehingga Ω = TT^τ. Diberikan P^τ = ΛΛ ~/²²

Model regresi Y x Xβ + ε dapat ditransformasi dengan mengalikan matriks P sehingga diperoleh:

PY x PXβ + Pε

Atau

Y* x X*β + ε*

Variansi pada ε* adalah

E{ε*ε*^τ} x Pσ²ΩP^τ = σ²1

Oleh karena itu, dalam mengestimasi dengan GLS dibutuhkan matriks P yang merupakan dekomposisi dari matriks Ω. Akan tetapi dalam prakteknya matriks Ω sulit untuk ditentukan, maka secara praktis menurut Gujarati [2] GLS diperkhusus dengan melihat pada pola yang ditunjukkan sisaan terhadap variabel X yang disebut dengan Weigted Least Square (WLS) yaitu beberapa melakukan pembobotan dengan

Jxi¹XS E(γi'7ι .

• 1.3    Heteroskedastisitas

Menurut Widarjono[6]    terdapat

konsekuensi terhadap estimator OLS jika ada masalah heteroskedastisitas namun tetap mempertahankan asumsi metode OLS dan ada kemungkinan tidak akan menghasilkan estimator linear tidak bias yang terbaik, apabila varian     estimator            mengandung

heteroskedastisitas maka variansnya sebagai berikut:

Var (S₁) = ∑⅛ ; i = 1,2.....n (∑χ t )

sementara itu varian estimator β₁ tanpa masalah heteroskedastisitas adalah sebagai berikut:

«²

Var (βι) = --t ∑ ^ i

Dengan demikian adanya heteroskedastisitas menyebabkan estimator β_i tidak lagi mempunyai varians yang minimum jika menggunakan metode OLS. Oleh karena itu, estimator β_i yang didapatkan akan mempunyai karakteristik sebagai berikut:

• a. Estimator metode OLS masih tidak bias b. Estimator metode OLS masih linier c. Namun estimator metode OLS tidak lagi mempunyai varians yang minimum (no longer best )

Jadi dengan adanya heteroskedastisitas, estimator OLS tidak menghasilkan estimator yang Best Linear Unbiased Estimator (BLUE).

Dalam       kenyataannya,       asumsi

homoskedastisistas dari kesalahan pengganggu ε mungkin tidak bisa dipenuhi, dengan kata lain varian dari kesalahan pengganggu bersifat heteroskedastisitas, yaitu E(εI ) = σj². Hal ini dapat dipahami jika diperhitungkan factor-faktor yang menjadi penyebab adanya kesalahan pengganggu ε dalam model regresi. Faktor kesalahan pengganggu ε dimasukkan kedalam model untuk dapat memperhitungkan kesalahan-kesalahan yang mungkin terjadi dalam pengukuran dan kesalahan karena mengabaikan variabel-variabel        tertentu.        Untuk

memperkirakan bahwa ε bervariasi secara sistematis dengan variabel bebas X.

Konsekuensi dari pelanggaran asumsi homoskedastisitas adalah sebagai berikut:

• 1.    Penduga (estimator) yang diperoleh tetap memenuhi persyaratan tidak bias. Sifat ketidakbiasan tidak tergantung pada varian galat. Jika dalam model regresi ada heteroskedastisitas,   maka kita tetap

memperoleh nilai parameter yang tidak bias karena sebagai penduga tidak bias tidak memerlukan asumsi bahwa varian galat harus konstan.

• 2.    Varian penduga yang diperoleh akan menjadi tidak efisien, artinya penduga tersebut tidak memiliki varian terkecil diantara penduga-penduga tidak bias lainnya.

Namun asumsi ini sangat penting artinya dalam analisis regresi mengingat kaitannya dengan estimasi standar error koefisien regresi. Sebagaimana diketahui bahwa standar error ini memiliki peran dalam pembentukan t hitung maupun F hitung yang berkaitan akan menjadi terlalu (overestimed) yang mungkin selanjutnya menghasilkan kesimpulan bahwa kasus spesifik β₁ adalah kelihatannya signifikan, walaupun sebenarnya tidak signifikan. Oleh karena itu jika asumsi homoskedastisitas tidak dipenuhi maka hasil uji t tidak menentu. Berdasarkan yang kita ketahui:

t = —

Dari penjelasan di atas, heteroskedastisitas merupakan masalah yang berpotensi serius, karena mungkin merusak seluruh bangun standar, demikian pula dengan prosedur pengujian hipotesis dan estimator OLS yang begitu rutin digunakan. Untuk itu, dalam segala studi kongkret, khususnya yang melibatkan data lintas-sektoral (cross section), kita mesti menentukan apakah menghadapi masalah heteroskedastisitas.

Menurut Gujarati [3], untuk mendeteksi masalah heteroskedastisitas dapat dilakukan dengan metode formal dan informal. Metode formal dapat dilakukan dengan uji statistika diantaranya Uji park, Uji White, Uji Glejser, Uji Korelasi rank dari Spearmen, dan Uji Breusch Pagan Godfrey (BPG). Dalam tulisan ini akan digunakan Breusch Pagan Godfrey (BPG) dalam mendeteksi masalah heteroskedastisitas.

• 2.    METODE PENELITIAN

Langkah-langkah yang dilakukan pada penelitian ini adalah:

• 1.    Membuat model awal pada regresi linier berganda dengan menggunakan metode OLS.

• 2.    Setelah memperoleh persamaan regresi, kemudian dilakukan pengujian untuk melihat

Tabel 1. Anova

Sumber Variansi	JK	Df
Regresi	7210,980	2
Sisaan	2112,408	82
Total	9323,388	84

a. Dependent Variable: Y

b. Predictors: (Constant), X2, X1

apakah terdapat masalah heteroskedastisitas atau tidak dengan menggunakan uji BPG.

• 3.    Tahap berikutnya adalah melakukan perbaikan pada model awal menggunakan metode WLS yaitu pembobotan data dengan suatu faktor pengali (pembobot) yang tepat, dalam penelitian ini pembobotan yang

Ill     1

diberikan adalah ,  ,     , dan

√ ,    ,(Yt)^,              σt

(residual kuadrat).

• 4.    Kemudian kembali menggunakan prosedur OLS terhadap data yang telah diboboti. Lalu menganalisa kembali pada data yang telah diboboti tersebut apakah masih mengandung heteroskedastisitas.

• 5.    Tahap terakhir yaitu melakukan uji heteroskedastisitas kembali dengan uji BPG, sehingga model memenuhi asumsi homoskedasisitas.

• 3.    HASIL DAN PEMBAHASAN

  • 3.1    Uji Heteroskedastisitas

Heteroskedatisitas secara nonformal, digunakan untuk mendeteksi adanya heteroskedastisitas dengan melihat ada tidaknya pola tertentu, grafiknya sebagai berikut:

Siettflipw

Dependent Veneble HH

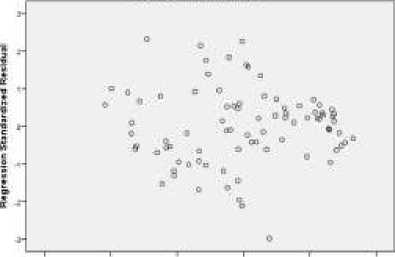
ReflfMiIe* StaMMdix »4 PredItWd VAee

Dari gambar [3] dapat disimpulkan bahwa terdapat pola sebaran yang menunjukkan titik-titik yang terus-menerus bergerak mendekati nol. Berdasarkan pola tesebut mengindikasikan adanya heteroskedastisitas. Jika diketahui

bentuk spesifik dari heteroskedastisitas pada gambar, maka dapat melakukan pembobotan

terhadap variabel terikat dan variabel bebas

sesuai dengan bentuk heteroskedastisitasnya.

Namun pada gambar [3] sulit untuk

mengidentifikasi pola sebarannya, oleh karena itu usaha perbaikan model untuk menghilangkan heteroskedastisitas akan diboboti dengan ,  ,

√

i(^ ₎, dan  .

Agar mendapat hasil yang lebih pasti untuk melihat adanya heteroskedastisitas atau

tidak, terdapat beberapa uji yang dapat dilakukan. Salah satunya yang digunakan di dalam penelitian ini adalah Uji Breusch Pagan Godfrey (BPG).

Hipotesis:

H0       : tidak ada heteroskedastisitas

H1       : ada heteroskedastisitas

Kriteria uji BPG adalah jika:

P-value ≤ a , maka H0 ditolak

P-value > a , maka H0 diterima

Dengan menggunakan SPSS 20 diperoleh tabel Anova berikut:

Berdasarkan tabel 1 diperoleh nilai varian:

₉ RSS

= n 2112,408

⁼   85

= 24,85

Kemudian diregresikan tehadap sisaan kuadrat yang dibagi dengan nilai varian, modelnya sebagai berikut:

e²

=   +PiPP_l + P₂ IPK_i + v_i

Dengan menggunakan SPSS 20 diperoleh tabel Anova berikut:

Tabel 2. Anova

Sumber Variansi	JK	Df	R2
Regression	14,909	2	0,071
Residual	194,946	82
Total	209,854	84

a. Dependent Variable: ujiBPG

b. Predictors: (Constant), X2, X1

Sehingga diperoleh Xhitung dan Xtabel sebagai berikut

₂ _TSSx R² Xhitung⁼2

209,854 X 0,071 ⁼2 = 7,45 2     __ 2

Xtabel =   ;db

=   ,05;2

= 5,95

Dapat disimpulkan bahwa hasil pengujian terhadap heteroskedastisitas dengan uji BPG pada taraf a sebesar 0,05 diperoleh nilai Xhitung > %tabel. Berdasarkan kriteria pengujian, maka keputusan yang diambil adalah tolak H0 atau data mengalami heteroskedastisitas.

• 3.2    Estimasi Dengan WLS

Berdasarkan perhitngan dengan metode BPG diperoleh bahwa H0 ditolak yang artinya terdapat masalah Heteroskedastisitas dalam model, sehingga diperlukan adanya perbaikan pada model agar tidak menyesatkan kesimpulan.

Persoalan     heteroskedastisitas     dapat

ditangani dengan melakukan pembobotan suatu faktor yang tepat kemudian menggunakan metode OLS terhadap data yang telah diboboti. Pemilihan terhadap suatu faktor untuk pembobotan tergantung bagaimana sisaan berkorelasi dengan X atau Y, jika sisaan proporsional terhadap ^i maka model akan dibagi dengan √ Xi, jika sisaan adalah proporsional dengan Xi sehingga model akan dibagi dengan Xi , selain proporsional dengan Xi dan Xi bisa juga diasumsikan bahwa pola varian sisaan adalah proporsional dengan [E( Yi)] ² sehingga dibagi dengan E( Y_i). Namun dalam prakteknya tidak selalu dengan pembobotan Ill

,  ,     dapat mengatasi heteroskedastisitas

√         (^γi)

karena sesungguhnya pembobot yang diberikan bergantung pada pola sebaran sisaan terhadap variabel bebas maupun variabel terikat. Oleh karena itu, dalam penelitian ini faktor pembobot Ill   1

yang akan dianalisis adalah , ,     , dan

√ , , (Yt ₎, an

(residual kuadrat).

Berikut ini koefisien determinasi R² setelah dilakukan pembobotan, yaitu:

Tabel 3. Hasi Estimasi WLS

No.	Faktor Pembobot	Koefisien Determinasi R2 I
1	1 √PPi         \	0,84
2	1 √ IPRt        \	0,49
3	1 PPi	0,78
4	1 EPKi	0,07
5	1 E( Yi )	0,67
6	1	0,99

Berikut ini hasil uji heteroskedastisitas dengan metode BPG yang telah diboboti.

Tabel 4. Hasil Uji Heteroskedastisitas dengan BPG

No .	Z2 Hitung	Z2 Tabel	Kesimpulan
1	16,42	5,95	Heteroskedastisitas
2	28,01	5,95	Heteroskedastisitas
3	19,63	5,95	Heteroskedastisitas
4	12,31	5,95	Heteroskedastisitas
5	7,30	5,95	Heteroskedastisitas
6	0,18	5,95	Homoskedastisitas

1

Dapat disimpulkan bahwa pembobot pada taraf a sebesar 0,05 dapat mengatasi heteroskedastisitas dengan diperoleh nilai Xhitung < Xtabel . Berdasarkan kriteria pengujian, maka keputusan yang diambil adalah terima H0 atau data tidak mengalami heteroskedastisitas.

• 4.    KESIMPULAN DAN SARAN

Berdasarkan hasil yang telah diperoleh maka dapat disimpulkan bahwa faktor pembobot yang dicobakan pada metode WLS dalam penelitian ini adalah 4=, ⅛, —, — , —^-, dan √⅛'√⅛'χι'×2 'E(γ_iγ 1

(residual kuadrat). Berdasarkan hasil uji BPG dengan menggunakan nilai a sebesar 0,05, sesuai kriteria pengujian diperoleh faktor 1

pembobot yang tidak signifikan adalah yang ^σi

artinya varian dari error bersifat konstan atau homoskedastisitas dengan R² sebesar 99%,

1 111

sedangkan faktor pembobot -:=,-:=, — ,— √^l √^2 ^l ^2

'^e(y^ masih singnifikan. Maka pada penelitian ini faktor pembobot yang tepat adalah .

^σi

Pada penelitian ini model yang digunakan adalah regresi linier berganda, jika ingin melakukan penelitian serupa, peneliti menyarankan menggunakan model nonlinier.

DAFTAR PUSTAKA

• [1]    Greene, W.H. 2003. Econometrics Analysis.

Fifth Edition. New Jersey: Prentice Hall.

• [2]    Gujarati, Damodar. 1995. Basic

Econometrics. Third Edition. Singapore: McGraw-Hill

• [3]    Gujarati, Damodar. 2007. Dasar-dasar Ekonometrika. Edisi Ketiga. Diterjemahkan oleh Julius A. Mulyadi dan Yelvi Andri. Jakarta: Erlangga.

• [4]    Neter, J.at all. 1997. Model Linear Terapan Buku I dan II: Analisis Regresi Linear Sederhana dan Analisis Regresi Ganda, diterjemahkan oleh Bambang Sumantri. Bogor: Jurusan Statistika FMIPA IPB.

• [5]    Uthami, P. 2013. Regresi Kuantil Median Untuk Mengatasi Heteroskedastisitas Pada Analisis Regresi. Skripsi. Universitas Udayana: Bali.

• [6]    Widarjono. 2005. Analisis Statistika Multivariat Terapan. UPP STIM YKPN. Yogyakarta.

25