APLIKASI MULTIVARIATE MULTIPLE REGRESSION UNTUK MENDUGA FAKTOR-FAKTOR YANG MEMENGARUHI KESEJAHTERAAN MASYARAKAT

E-Jurnal Matematika Vol 3 (3), Agustus 2014, pp. 100-106

ISSN: 2303-175

APLIKASI MULTIVARIATE MULTIPLE REGRESSION UNTUK MENDUGA FAKTOR – FAKTOR YANG MEMENGARUHI KESEJAHTERAAN MASYARAKAT

Putu Eka Swastini¹, I Komang Gde Sukarsa², I Putu Eka N. Kencana^§3

• ¹    Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ²    Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ³    Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

• ^§ Corresponding Author

ABSTRACT

This essay aimed to apply the Multivariate Multiple Regression (MMR) method for the welfare issue. The predictor variables in the model are 18 indicators of welfare according to Indonesian Central Bureau of Statistic (BPS) and the response variables are Human Development Index (IPM), Gross Regional Domestic Product (PDRB), and Regional Crime Index (IKD). In modeling the relationship between q responses (y!,..., y! ) and a single set of predictor variables (x!,..., x! ), MMR assumed each pairs of two response variables were correlated and its distribution follows normal multivariate. Based on the result of MMR, we obtained six out of 18 predictor variables simultaneously affect IPM and PDRB. The final model showed the association between those variables very closed to 100 percent.

Keywords: GLM, multivariate, regression, welfare

• 1.    PENDAHULUAN

Kesejahteraan masyarakat merupakan suatu konsep multiindikator yang menunjukkan ukuran keberhasilan pembangunan di suatu wilayah. Sebagai sebuah konsep, pengukuran mengenai kesejahteraan masyarakat mengalami berbagai perkembangan. Pada tahun 1970-an, tingkat kesejahteraan masyarakat diukur menggunakan besaran Produk Domestik Bruto (PDB) atau pendapatan per kapita yang diperoleh dengan membagi PDB dengan total penduduk di suatu negara. Meningkatnya pemahaman mengenai peran dimensi non-ekonomi pada pengukuran kesejahteraan masyarakat menyebabkan PDB sebagai indikatornya menuai banyak kritik. Selanjutnya, pengukuran tingkat kesejahteraan mulai melibatkan dimensi sosial, politik, dan budaya [1].

Salah satu ukuran yang mengakomodasikan dimensi-dimensi non-ekonomi dalam mengukur kesejahteraan masyarakat adalah konsep tentang Indeks Pembangunan Manusia (IPM) yang diintroduksi oleh United Nation Development Program (UNDP). Selain PDB atau Produk Domestik Regional Bruto (PDRB) bila wilayah kajian adalah provinsi dan IPM, ukuran yang

juga biasa digunakan untuk menyatakan tingkat kesejahteraan masyarakat suatu provinsi adalah Indeks Kriminalitas Daerah (IKD) [1].

Badan Pusat Statistik (BPS) Indonesia, sebagai lembaga pemerintah yang ditugaskan untuk mengadministrasi data dan informasi di Indonesia, mengintroduksi 18 indikator tentang kesejahteraan masyarakat Indonesia, yaitu: (a) Laju Pertumbuhan Penduduk (LPP); (b) Kepadatan Penduduk per km² (KPP); (c) Angka Melek Huruf (AMH); (d) Rata-rata Lama Sekolah (RLS); (e) Angka Harapan Hidup (AHH); (f) Pengeluaran per Kapita (PPK); (g) Persentase Rata-rata Pengeluaran untuk Konsumsi Makanan (PKM); (h) Persentase Rumah Tangga yang Memiliki Fasilitas Minum Sendiri (FMS); (i) Persentase Rumah Tangga dengan Jenis Lantai Bukan Tanah (LBT); (j) Persentase Rumah Tangga dengan Luas Lantai < 20 m² (LLK); (k) Persentase Rumah Tangga dengan Dinding Tembok (RDT); (l) Persentase Rumah Tangga dengan Sumber Penerangan dari PLN (PLN); (m) Persentase Rumah Tangga dengan Fasilitas Buang Air Besar Sendiri (BAB); (n) Persentase Penduduk Miskin (RTM); (o) Jumlah Pengangguran Terbuka (JPT); (p) Persentase Penduduk yang Mengalami Keluhan Kesehatan Sebulan

yang Lalu (PKK); (q) Persentase Penduduk Mengalami Keluhan Kesehatan dan Kegiatannya Terganggu (PPB); dan (r) Jumlah Penduduk Bekerja (JPB) [2].

Mencermati PDRB, IPM, dan IKD merupakan tiga ukuran yang lazim digunakan untuk menyatakan tingkat kesejahteraan masyarakat [1] dan terdapat 18 indikator pengukurnya [2], maka model kausal pengaruh seluruh variabel indikator terhadap masing-masing ukuran kesejahteraan masyarakat dapat dibangun menggunakan model analisis regresi linier berganda. Meski demikian; bila PDRB, IPM, dan IKD tidak saling bebas satu dengan lainnya, sesungguhnya model analisis regresi multivariate berganda (Multivariate Multiple Regression/MMR) lebih layak untuk digunakan.

Dalam MMR, proses penghitungan untuk mengetahui kontribusi sekelompok variabel prediktor terhadap sekumpulan variabel respon dilakukan serempak dengan memperhatikan korelasi antarvariabel respon [3]. Jadi, pengaruh dari 18 indikator kesejahteraan masyarakat seperti diungkap oleh BPS terhadap PDRB, IPM, dan IKD – dengan menggunakan MMR – bisa dilakukan secara serempak.

Penelitian ini dimotivasi oleh keinginan untuk membentuk model kausal antara 18 indikator kesejahteraan masyarakat dengan ketiga ukuran kesejahteraan yang dibangun dengan mengaplikasikan metode MMR. Model yang terbentuk selanjutnya dapat digunakan sebagai model peubah ganda yang mampu menggambarkan kondisi kesejahteraan masyarakat di 33 provinsi di Indonesia.

Bagian-bagian selanjutnya dari tulisan ini disusun mengikuti bentuk berikut: bagian meto-delogi penelitian menguraikan tahapan riset; bagian hasil dan pembahasan menguraikan hasil analisis secara deskriptif dan konfirmatif serta model MMR yang diperoleh; dan pada bagian penutup terisi kesimpulan dari riset.

• 2.    METODE PENELITIAN

Penelitian ini tergolong ke dalam jenis penelitian non-experimental dengan data yang digunakan merupakan data sekunder yang diperoleh dari BPS Indonesia [2]. Pengembangan model kausal antara ketiga variabel respon dan seluruh variabel prediktor dilakukan mengikuti tahapan-tahapan berikut:

• (a)    Melakukan standarisasi seluruh variabel pada matriks data;

• (b)    Memeriksa matriks korelasi antarvariabel respon;

• (c)    Memeriksa asumsi matriks data mengikusi sebaran normal multivariate;

• (d)    Mengestimasi parameter-parameter model; (e) Memeriksa signifikansi parameter model;

• (f)    Memeriksa pengaruh parsial dari masing-masing variabel prediktor. Prediktor yang tidak nyata dieleminasi dari tahapan selanjutnya;

• (g)    Merevisi model dengan menyertakan hanya variabel-variabel prediktor yang signifikan pada model sebelumnya;

• (h)    Memeriksa residual model, dan;

• (i)    Melakukan interpretasi model akhir.

• 3.    HASIL DAN PEMBAHASAN

• A.    Analisis Deksriptif

Analisis deskriptif dilakukan terpisah untuk masing-masing kelompok variabel pada matriks data kesejahteraan masyarakat di-33 provinsi di Indonesia pada tahun 2012. Pemeriksaan awal menunjukkan variabel PPB tidak dapat disertakan pada analisis memperhatikan jumlah data hilang mencapai 22 amatan dari total 33 amatan provinsi, sehingga jumlah prediktor pada model berkurang satu. Tabel 1 dan 2 menunjukkan deskripsi dari kedua kelompok variabel:

Tabel 1. Deskripsi Kelompok Variabel Prediktor

Variabel	Mean	Simpangan Baku	Koefisien Keragaman
LPP	1,90	1,12	58,95
KPP	705,12	2 561,40	363,26
AMH	94,06	5,02	5,34
RLS	8,29	0,87	10,49
AHH	69,23	2,39	3,45
PPK	635,95	13,78	2,17
PKM	339,66	67,19	19,78
FMS	54,38	14,70	27,03
LBT	93,99	6,53	6,95
LLK	6,07	6,04	99,51
RDT	58,28	20,58	35,31
PLN	82,63	15,73	19,04
BAB	63,78	12,59	19,74
RTM	12,65	6,73	53,20
JPT	5,33	2,47	46,34
PKK	27,75	5,39	19,42
JPB	94,64	2,19	2,31

Sumber: Analisis Data (2014)

Tabel 2. Deskripsi Kelompok Variabel Respon

Variabel	Mean	Simpangan Baku	Koefisien Keragaman
IPM	72,87	2,90	3,98
PDRB	3,03	2,77	91,42
IKD	10,34	10,59	102,42

Sumber: Analisis Data (2014)

Tabel 1 menunjukkan kepadatan penduduk per km² (KPP) memiliki koefisien keragaman terbesar, dan pengeluaran per kapita (PPK) memiliki koefisien keragaman terkecil. Pada kelompok variabel respon, IPM dan IKM merupakan variabel-variabel dengan koefisien keragaman terkecil dan terbesar (Tabel 2).

Memperhatikan bahwa MMR mensyaratkan agar antarvariabel respon berkorelasi, maka secara deskriptif hal ini bisa dilakukan dengan memperhatikan plot dua dimensi antarvariabel seperti gambar 1:

Plot Matriks Variabel Respon IPM, PDRB dan IKD

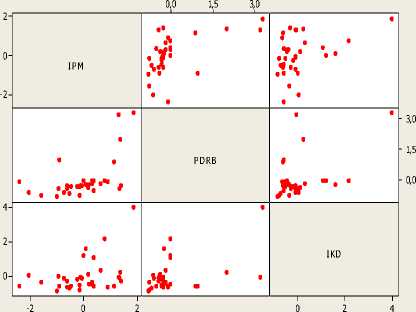
Gambar 1. Plot Hubungan Antarvariabel Respon

Pemeriksaan secara deskriptif mengindikasikan pola-pola hubungan yang tak acak antara pasangan variabel respon pada model. Hal ini tercermin dalam plot pada gambar 1.

• B.    Pengujian Hubungan Korelasional

antarvariabel Respon

Meski secara deskriptif telah terlihat adanya pola korelasional antarvariabel respon, analisis konfirmatif perlu dilakukan dengan memeriksa matriks korelasi melalui Uji Bartlett pada hipotesis berikut:

H0 : Matriks korelasi adalah matriks identitas H1 : Matriks korelasi bukan matriks identitas

Bila matriks korelasi berukuran q x q dan q menyatakan jumlah variabel, statistik Bartlett

akan memiliki distribusi /^! dengan derajat bebas sebesar - q(q - 1). Statistik Bartlett bisa dihitung dengan formula berikut:

/.«     = — (n - 1 — -7-) ln ∣Corr∣      (1)

Pada pers. (1), |Corr| menyatakan determinan dari matriks korelasi. Menggunakan pers. (1) diperoleh /[-#$%&$$= 19,85; lebih besar dari nilai χ;,," _;! = 7,82. Jadi H₀ ditolak pada taraf nyata sebesar 5 persen dan membuktikan secara kon-firmatif antarvariabel respon berkorelasi; sebuah kondisi yang dipersyaratkan pada analisis MMR.

• C.    Pengujian Asumsi Normal Multivariate pada

Variabel-variabel Respon

Pengujian asumsi normal multivariate pada variabel respon dilakukan dengan menghitung Jarak Mahalonobis amatan ke - i (d!) melalui formula berikut:

di = (y. - y)^! ∑^!! (y. - y); i = 1, •••, n (2)

Pada pers. (2); y∣, y, dan Σ masing-masing menyatakan nilai amatan ke – i pada vektor variabel respon Y, vektor nilai tengah dari masing-masing variabel, dan matriks ragam peragam antarvariabel. Statistik di memiliki distribusi /^! dengan derajat bebas sebesar q (jumlah variabel respon). Kriteria penerimaan dari pasangan hipotesis berikut:

H0 : Amatan ke – i mengikuti sebaran normal multivariate

H1 : Amatan ke – i tidak mengikuti sebaran normal multivariate

ditentukan dengan membandingkan di terhadap nilai χ↑ ,_i dengan v menyatakan tingkat signifikansi uji. Bila di ≤ χ²_n maka H₀ tidak dapat

^,4

ditolak. Secara agregat, bila jumlah amatan yang mengikuti sebaran normal multivariate melebihi separuh dari total amatan, maka bisa disimpulkan data mengikuti sebaran normal multivariate.

Penghitungan yang dilakukan menunjukkan 30 nilai di lebih kecil dari nilai Zq05.3 = 2,366 atau kurang lebih 90,1 persen amatan mengikuti sebaran normal multivariate. Merujuk [5] bisa disimpulkan vektor variabel respon menyebar normal multivariate.

• D.    Pengujian Multikolinearitas pada Variabel-

variabel Prediktor

Agar sebuah model regresi bersifat valid, maka antarvariabel prediktor yang disertakan dalam model seharusnya tidak berkorelasi. Salah

satu ukuran yang sering digunakan untuk memeriksa kolinearitas antarvariabel prediktor adalah nilai Variance Inflation Factors (VIFs). Bila Rj menyatakan proporsi ragam variabel prediktor ke–i yang berasosiasi dengan variabel-variabel prediktor lainnya, maka total ragam variabel ke–i yang tidak terkait dengan variabel-variabel pre-diktor lainnya adalah 1 - Rj. VIF, sebagai ukuran multikolinearitas, dapat dinyatakan dalam persamaan (3):

^v,f' = (3)

Merujuk nilai VIF pada pers. (3), sebuah variabel prediktor diputuskan tidak memiliki multikolinearitas dengan prediktor lainnya bila nilai VIF lebih kecil dari 10 [6]. Penghitungan nilai VIF yang dilakukan dengan menggunakan program Minitab memberikan hasil berikut:

Tabel 3. Nilai VIF dari Masing-masing Prediktor

Variabel Prediktor	Nilai VIF	Variabel Prediktor	Nilai VIF
LPP	3,3	LLK	2,8
KPP	3,6	RDT	2,2
AMH	3,5	PLN	5,7
RLS	5,6	BAB	3,6
AHH	2,5	RTM	3,1
PPK	4,4	JPT	7,1
PKM	9,0	PKK	2,0
FMS	3,7	JPB	8,1
LBT	3,5

Sumber: Analisis Data (2014)

Tabel 3 menunjukkan seluruh variabel pre-diktor memiliki nilai VIF < 10 yang menjustifi-kasi bahwa antarvariabel tidak terjadi multikoli-nearitas. Meski demikian, memperhatikan PKM (persentase rata-rata pengeluaran untuk konsumsi makanan), JPB (jumlah penduduk bekerja), dan JPT (jumlah pengangguran terbuka) merupakan tiga prediktor dengan nilai VIF yang relatif lebih tinggi dibandingkan prediktor lainnya; interpretasi pengaruh masing-masing variabel ini dalam model harus dilakukan secara cermat.

• E.    Estimasi Parameter dan Uji Signifikansi

Mempertimbangkan asumsi antarvariabel respon saling berkorelasi dan matriks variabel respon mengikuti distribusi normal mutivariate, maka estimasi parameter model dan uji signifikasinya bisa dilanjutkan. Tabel 4 menunjukkan estimasi parameter pada full model MMR meng™

gunakan prosedur GLM pada SAS 9.13:

Tabel 4. Analisis MMR dengan Prosedur GLM

Variabel Prediktor	Variabel Respon
	IPM	PDRB	IKD
Konstan	-0,0000	0,0000	0,0000
LPP	0,0086	0,2301	-0,2432
KPP	0,0007	0,3546	0,8721
AMH	0,3882	-0,1091	0,0371
RLS	0,2254	0,1473	-0,1598
AHH	0,4584	-0,0228	-0,0127
PPK	0,3700	0,5093	0,3079
PKM	-0,0088	0,0851	-0,0305
FMS	0,0038	0,2153	0,1554
LBT	-0,0040	-0,0813	-0,0171
LLK	0,0052	0,2045	-0,0728
RDT	-0,0032	-0,1454	-0,0795
PLN	0,0032	-0,4989	0,0295
BAB	-0,0018	0,2378	-0,0518
RTM	-0,0007	-0,0245	0,2116
JPT	-0,0055	0,3079	0,3761
PKK	0,0010	-0,0108	-0,3154
JPB	-0,0061	0,0548	0,3093
R2 (%)	99,9999	89,6671	76,5175
RMSE	0,0109	0,4695	0,7078
Signifikansi	< 0,0001	0,0001	0,0228

Sumber: Analisis Data (2014)

Tabel 4 memperlihatkan model MMR dari ketiga variabel respon dan 17 variabel prediktor signifikan pada taraf uji 5 persen. Berturut-turut model untuk IPM, PDRB, dan IKD memiliki koefisien determinasi dengan nilai 99,99 persen; 89,67 persen; dan 76,52 persen.

Agar pengaruh dari masing-masing variabel prediktor secara simultan terhadap ketiga variabel respon diketahui, maka dilakukan pengujian pasangan hipotesis berikut:

H0 : B = 0

H1 : B ≠ 0

∕ ^β∣" ^β∣" ^β∣" \

dengan B = I                  I dan 0 adalah

'^β!"!      ^e!"# ^e!"# '

matriks berukuran 18 x 3 dengan nilai untuk setiap unsur matriks sama dengan nol.

Pengujian pasangan hipotesis di atas dilakukan dengan Uji Wilks Lambda dengan statistik uji bisa dinyatakan pada persamaan (4):

Λ=

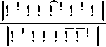
(4)

Pada pers. (4) statistik Λ akan berdistribusi mengikuti distribusi Wilk’s Lambda. Hipotesis

nol ditolak bila Λ ≤ Λ∣ .∣ .∣ .∣ ∣ ∣ ∣ ∣ dengan p, q, dan n menunjukkan jumlah variabel prediktor, jumlah variabel respon, dan jumlah amatan. Penghitungan yang dilakukan menggunaan pers. (4) memberikan nilai Λ sebesar 0,002 x 10^-3; lebih kecil dari nilai kritis Wilks Lambda untuk taraf signifikansi 5 persen sebesar 0,397. Memperhatikan hal ini, maka H0 ditolak dan sekurang-kurangnya terdapat sebuah prediktor yang secara serempak berpengaruh terhadap IPM, PDRB, dan IKD.

Memperhatikan uji signifikansi parameter secara simultan menunjukkan setidak-tidaknya terdapat sebuah variabel prediktor yang berpengaruh secara nyata terhadap ketiga variabel respon, maka uji dilanjutkan untuk memeriksa pengaruh dari masing-masing variabel prediktor terhadap ketiga variabel respon. Uji ini dilakukan menggunakan sub-prosedur MANOVA dari GLM pada SAS^™ 9.13 dengan hasil uji sebagai berikut:

Tabel 5. Uji Signifikasi Parameter Model

Variabel Prediktor	Wilks’ Lambda	Nilai F	p-Value
LPP	0,5447	3,62	0,043 *
KPP	0,4772	4,75	0,019 *
AMH	0,0013	3460,66	< 0,0001 **
RLS	0,0058	742,39	< 0,0001 **
AHH	0,0006	6917,28	< 0,0001 **
PPK	0,0017	2531,17	< 0,0001 **
PKM	0,8656	0,67	0,584 ns
FMS	0,8142	0,99	0,484 ns
LBT	0,8972	0,50	0,691 ns
LLK	0,7006	1,85	0,877 ns
RDT	0,8297	0,89	0,473 ns
PLN	0,6938	1,91	0,177 ns
BAB	0,8570	0,72	0,556 ns
RTM	0,9280	0,34	0,799 ns
JPT	0,7935	1,13	0,374 ns
PKK	0,8058	1,04	0,406 ns
JPB	0,8686	0,66	0,594 ns

Sumber: Analisis Data (2014)

Keterangan:

* : nyata pada taraf uji 5 persen

** : nyata pada taraf uji 1 persen

ns : tidak nyata pada taraf uji 5 persen

Mencermati nilai-nilai p-value pada Tabel 5, hanya enam dari 17 variabel prediktor yang berpengaruh secara nyata terhadap ketiga variabel respon dari model. Memperhatikan hal ini, maka model penuh dengan hasil tercantum pada Tabel 4 direduksi (reduced model) dengan menyertakan

hanya enam variabel prediktor yang terbukti signifikan sebagai prediktor pada model yang direduksi. Hasil analisis diperlihatkan pada Tabel 6:

Tabel 6. Analisis MMR untuk Model Direduksi

Variabel Prediktor	Variabel Respon
	IPM	PDRB	IKD
Konstan	0,0000	0,0000	0,0000
LPP	0,0011 ns	0,5134 **	-0,1788 ns
KPP	-0,0002 ns	0,5460 **	0,7061 **
AMH	0,1760 **	0,0714 ns	0,0086 ns
RLS	0,0873 **	-0,0049 ns	-0,0167 ns
AHH	0,0272 **	0,0135 ns	0,0037 ns
PPK	0,3230 **	0,2284 *	0,1373 ns
R2 (%)	99,9893	68,1404	63,1611
RMSE	0,0118	0,6262	0,6736
Signifikansi	< 0,0001	< 0,0001	0,0001
Sumber: Analisis Data (2014)
Keterangan: * : nyata pada taraf uji 5 persen ** : nyata pada taraf uji 1 persen ns : tidak nyata pada taraf uji 5 persen

Pemeriksaan signifikansi dari masing-masing model variabel respon menunjukkan IPM, PDRB dan IKD dijelaskan secara signifikan oleh variabel-variabel prediktornya. IPM memiliki empat variabel prediktor dengan pengaruh parsial yang signifikan, sedangkan PDRB dan IKD masing-masing hanya dipengaruhi secara signifikan oleh tiga dan satu variabel prediktor. Berturut-turut IPM, PDRB, dan IKD terjelaskan oleh variabel-variabel penyusunnya sebesar 99,99 persen; 68,14 persen; dan 63,15 persen.

• F.    Pemeriksaan Residual Model

Sebelum interpretasi model dapat dilakukan, akan sangat baik residual dari model tereduksi diperiksa. Pemeriksaan residual difokuskan pada pemenuhan asumsi residual menyebar normal multivariate, pengujian kehomogenan ragam, dan pengujian independensi antar-residual:

• 1.    Pemeriksaan Asumsi Normal Multivariate

Pemeriksaan bahwa residual model menyebar normal multivariate dilakukan dengan mengamati nilai jarak Mahalanobis (dihitung dari pers. 2) atau d\ yang lebih kecil dari nilai ∕∣ ,_{r ;!} sebagai nilai kritis. Hasil penghitungan menunjukkan 31 residual memiliki nilai d'! lebih kecil dari nilai kritis. Dua amatan, amatan nomor 2 (Provinsi Sumatera Utara) dan nomor 23 (Provinsi Kalimantan Selatan), memiliki jarak Mahalanobis

melebihi nilai kritis. Memperhatikan kriteria dari [5], maka bisa disimpulkan residual dari model tereduksi mengikuti sebaran normal multivariate.

• 2.    Pemeriksaan Asumsi Kehomogenan Ragam

Asumsi kehomogenan ragam dari residual model diperiksa menggunakan Uji Bartlett dengan pasangan hipotesis yang diuji adalah:

Ho : σ/ = σγ = σ↑

H₁ : Setidak-tidaknya ada sepasang σ∣’ ≠ Oi’

Pasangan hipotesis di atas diuji dengan membandingkan nilai — terhadap nilai distribusi /^! dengan derajat bebas = (3 - 1) = 2. Keputusan uji untuk menolak H₀ bila — > ∕∖ _;!, dan m serta c masing-masing dihitung melalui tiga persamaan berikut:

^ς i''i7 ^- d (5)

m = ln s^! (∑!! ! v!) - In s∖ ∑∖_h v!          (6)

^s! = ⅛                (7)

Pada pers. (5), (6), dan (7); k menyatakan jumlah populasi, vi menyatakan ukuran populasi ke – i dikurangi satu, dan s² menyatakan ragam gabungan (pooled variance).

Hasil penghitungan menunjukkan nilai — sebesar 0,045; lebih kecil dari χ∖,_{r ;!} = 5,99. Jadi, H0 yang menyatakan bahwa ragam ketiga populasi residual homogen tidak bisa ditolak.

• 3.    Pemeriksaan Asumsi Independensi Residual

Independensi antarpopulasi residual model diperiksa menggunakan Bartlett’s Test of Sphericity. Uji ini memeriksa apakah matriks korelasi merupakan matriks identitas, dengan pasangan hipotesis uji adalah:

H0 : matriks korelasi adalah matriks identitas H1 : matriks korelasi bukan matriks identitas

Bila hasil uji menunjukkan H0 tidak bisa ditolak, bisa disimpulkan antarpopulasi (residual) saling bebas.

Penghitungan yang dilakukan pada residual model memberikan matriks korelasi (R) sebagai berikut:

R=

1 0,398 0,074

0,398 1 0,293

0,074 0,293

1

Mempergunakan pers. (1), diperoleh statistik Bartlett sebesar 7,98. Bila dibandingkan dengan nilai ∕∖ _{>r ;!} = 7,82 maka terlihat hipotesis nol ha-

rus ditolak pada taraf uji 5 persen. Hal ini menunjukkan bahwa antar-residual tidak bersifat independen. Hal ini diduga disebabkan oleh amatan nomor 2 dan 23 yang terklasifikasikan tidak menyebar normal multivariate dan cenderung berprilaku sebagai pencilan pada matriks data.

Pemeriksaan terhadap pemenuhan asumsi oleh residual model menghasilkan dua asumsi terpenuhi. Asumsi ketiga tidak terpenuhi diduga disebabkan oleh adanya pencilan pada matriks data. Mengacu kepada hasil ini, maka model MMR yang diperoleh layak diinterpretasikan.

• G.    Interpretasi Model

Model tereduksi sebagai model akhir seperti tercantum pada Tabel 6 memperlihatkan bahwa ketiga indikator dari kesejahteraan masyarakat Indonesia dipengaruhi oleh satu atau lebih dari enam variabel prediktor yang diintroduksi oleh BPS. Pada IPM, empat variabel prediktor mampu menjelaskan IPM sebesar 99,99 persen dengan pengaruh-pengaruh bersifat positif. Prediktor dengan pengaruh terbesar adalah Pengeluaran per Kapita (PPK) masyarakat disusul oleh Angka Melek Huruf (AMH).

Sementara itu, PDRB sebagai indikator kesejahteraan masyarakat yang kedua, terjelaskan secara signifikan oleh tiga prediktor dengan tipe pengaruh positif. Pengaruh terbesar diberikan oleh Kepadatan Penduduk per km² (KPP) disusul oleh pengaruh dari Laju Pertambahan Penduduk (LPP).

Indeks Kriminalitas Daerah sebagai indikator ketiga kesejahteraan masyarakat, hanya dipengaruhi secara signifikan oleh variabel Kepadatan Penduduk per km² (KPP) di mana semakin tinggi maka IKD semakin besar. Lima prediktor lain tidak terbukti secara signifikan mempengaruhi indikator ini.

Secara simultan, kemampuan keenam variabel untuk menjelaskan ketiga indikator kesejahteraan masyarakat bisa dicermati melalui nilai Eta Square (η∖ ) yang bisa dihitung dari 1 - Λ dengan Λ dihitung menggunakan pers.(4) [5]. Pada model MMR yang diperoleh, nilai η∖ sebesar 99,99 persen; sebuah ukuran yang sangat baik untuk menjelaskan hubungan antara ketiga indikator dengan enam prediktornya.

• 4.    SIMPULAN DAN SARAN

Merujuk kepada hasil yang diperoleh pada penelitian ini, maka simpulan dan saran untuk riset selanjutnya disampaikan sebagai berikut:

• A.    Simpulan

• 1.    Hanya enam dari 17 variabel prediktor yang secara simultan terbukti berpengaruh pada ketiga indikator kesejahteraan masyarakat. Keenam variabel ini adalah LPP, KPP, AMH, RLS, AHH, dan PPK;

• 2.    Secara terpisah, IPM dipengaruhi secara signifikan oleh AMH, RLS, AHH, dan PPK; dengan koefisien determinasi sebesar 99,99 persen;

• 3.    Secara terpisah, PDRB dipengaruhi secara signifikan oleh LPP, KPP, dan PPK; dengan koefisien determinasi sebesar 68,14 persen;

• 4.    Secara terpisah, IKD hanya dipengaruhi secara signifikan oleh KPP dengan koefisien determinasi sebesar 63,16 persen;

• 5.    Pada hubungan simultan antara keenam pre-diktor dengan ketiga indikator kesejahteraan masyarakat, model MMR yang diperoleh memiliki kemampuan untuk menjelaskan hubungan yang terbentuk sebesar 99,99 persen.

• B.    Saran

• 1.    Memperhatikan adanya potensi pencilan pada matriks data, pada penelitian berikutnya disarankan untuk melakukan pemeriksaan dan tindakan remedial terkait dengan potensi dari pencilan ini;

• 2.    Model MMR yang dibangun pada penelitian ini belum mempertimbangkan adanya efek interaksi antarvariabel prediktor. Peneliti berikutnya disarankan untuk membangun model yang mengakomodir pengaruh interaksi, khususnya pada enam variabel predik-tor yang terbukti memiliki pengaruh yang signifikan terhadap ketiga indikator.

DAFTAR PUSTAKA

• [1]    Badrudin, R., 2012. Ekonomika Otonomi Daerah. Yogyakarta: UPP STIM YKPN.

• [2]    BPS, 2013. Statistik Indonesia 2013. Jakarta: Badan Pusat Statistik.

• [3]    Johnson, Richard A, Wichern, Dean W. 1998. Applied Multivariate Statistical Analysis. Upper Saddle River: Prantice-Hall, Inc.

• [4]    Morrison, D.F., 1990. Multivariate Statistical Methods. 3^rd ed. Singapore: McGraw-Hill Inc.

• [5]    Rencher, A. C., 2002. Methods of Multivariate Analysis. 2^nd ed. Canada: A John Wiley & Sons, Inc.

• [6]    O’Brien, Robert M. “A Caution Regarding Rules of Thumb for Variance Inflation Factors”. Quality & Quantity, Vol. (41), pp. 673-90, 2007.

106