E-Jurnal Matematika Vol. 3 (4), November 2014, pp. 160 -167

ISSN: 2303-1751

APLIKASI ALGORITMA GENETIKA UNTUK MERAMALKAN KONSUMSI PREMIUM KOTA DENPASAR

Victor Mallang1, Ketut Jayanegara§2, Made Asih3, I Putu Eka N. Kencana4

§Corresponding Author

ABSTRACT

This research aimed to forecast the gasoline demand at Denpasar using genetic algorithm method. This algorithm was selected because of easy to implement and its ability to find acceptable solution quickly. This algorithm works by searching the best individu according to fitness function defined. The series data used in the research were 60 observations of monthly gasoline demand at Denpasar for period January 2009 through December 2013. By observing the Partial Autocorrelation Function (PACF) plot, we found the last lag before the series become stationer was sixth lag. Based on this finding, we decided the best individu was represented by six genes. This individu, in addition, was used to make in-sample forecasting. The forecasted data had mean absolute error (MAE) as much as 553,27 kiloliters. For one semester out-of sample forecast, we found gasoline consumption fluctuated with lowest and highest consumption were for February 2014 and June 2014, respectively.

Keywords: forecasting, gasoline demand, genetic

  • 1.    PENDAHULUAN

Berbagai teknik peramalan data runtun waktu senantiasa berkembang seiring dengan kebutuhan yang meningkat terhadap keakuratan hasil peramalan yang diperoleh. Secara umum, teknik peramalan data runtun waktu bisa diklasifikasikan ke dalam kelompok teknik peramalan statistika dan kelompok teknik peramalan non-statistika. Model-model moving average, pemulus eksponensial dan berbagai varian dari Autoregressive Integrated Moving Average (ARIMA) tergolong ke dalam kelompok pertama; dan fuzzy time series (FTS) serta algoritma genetika tergolong ke dalam kelompok kedua yang juga dikenal sebagai soft modeling technology [1].

Sebagai sebuah metode peramalan dalam kelompok soft modeling, algoritma genetika merupakan algoritma pencarian yang didasarkan kepada mekanisme seleksi genetika alamiah. Algoritma genetika dimulai dengan membentuk sejumlah solusi yang disebut populasi. Setiap

algorithm, MAE

solusi dari populasi pada algoritma ini diwakili oleh satu individu atau kromosom.

Algoritma genetika pada awalnya digunakan sebagai algoritma pencarian parameter-parameter pada permasalahan optimasi. Perkembangan berikut dari algoritma ini adalah mulai diaplikasikannya dalam berbagai ranah permasalahan seperti teori pembelajaran, pemrograman otomat, peramalan dan lainnya [2].

Bahan bakar minyak (BBM) merupakan komoditas yang memegang peranan sangat penting dalam semua aktifitas ekonomi khususnya sebagai bahan bakar kendaraan bermotor. Di Indonesia BBM yang digunakan pada kendaraan bermotor adalah premium, solar, biosolar, pertamax, dan pertamax plus yang diproduksi oleh PT. Pertamina [3].

Berdasarkan latar belakang yang telah dipaparkan, maka akan dilakukan sebuah penelitian yaitu tentang bagaimana peramalan jumlah kebutuhan BBM jenis premium menggunakan algoritma genetika.

  • 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini merupakan data sekunder yang diperoleh dari PT. Pertamina Bali. Data tersebut berupa data bulanan jumlah konsumsi premium kota Denpasar, periode Januari 2009 sampai Desember 2013.

Representasi kromosom yang digunakan pada penelitian ini adalah:

Zt = ao + aι Zt- 1 + a2Zt - 2 +......+ ^iZt—i (2.1)

dengan besar ai merupakan gen dan i = 1,2,3,..., k. Nilai k dilihat dari lag terakhir yang melebihi batas error sebelum data mencapai kestasioneran.

Terdapat 4 parameter genetika yang digunakan dalam penelitian ini, yaitu sebagai berikut:

  • 1.    generasi = 500 iterasi

  • 2.    npop = 50 individu

  • 3.    probabilitas crossover (Pcro s') = 80%

  • 4.    probabilitas mutasi (Pmut') = 50%

Langkah-langkah analisis data yang dilakukan dalam penelitian ini sebagai berikut:

  • 1.    Mencari model input.

  • a.    Plot data deret waktu untuk melihat apakah data sudah stasioner atau belum, data memiliki trend, dan linier.

  • b.    Jika data tidak stasioner, maka akan dilakukan differencing untuk menstasio-nerkan data.

  • c.    Setelah data stasioner maka akan dicari pola data berdasarkan plot ACF dan PACF, yang akan digunakan sebagai model input pada representasi kromosom algoritma genetika.

  • 2.    Mencari populasi, batas atas dan bawah selang pembangkit populasi acak, dengan meregresikan sampel data berdasarkan model input yang diperoleh.

  • 3.    Melakukan proses algoritma genetika untuk mendapat koefisien linier, dengan langkah-langkah sebagai berikut:

  • a.    Inisialisasi populasi awal.

  • b.    Evaluasi nilai fitness pada setiap individu dalam generasi menggunakan persamaan MAE = 1ei dengan ei = fa - zt∣

  • c.    Seleksi orang tua menggunakan metode steady state

  • d.    Melakukan crossover menggunakan persamaan

z’(k) = r.zi(k) + (1 - r).zi(k + 1)      (2.2)

z’(k + 1) = (1 — r). zi(k) + r. zi(k + 1)  (2.3)

  • e.    Melakukan mutasi dengan metode pemilihan nilai secara acak (random).

  • f.    Melakukan elitisme dan seleksi populasi baru. Ulangi langkah c sampai g sebanyak generasi.

  • g.    Individu yang memiliki nilai fitness terkecil akan menjadi model linier terbaik.

  • 4.    Melakukan peramalan  in-sample  jumlah

kebutuhan BBM jenis premium tahun 2009 sampai 2013.

  • 5.    Melakukan peramalan out of sample jumlah kebutuhan BBM jenis premium, pada Bulan Januari, Pebruari, Maret, dan April tahun 2014.

  • 3.    HASIL PENELITIAN DAN DISKUSI

Langkah awal yang dilakukan untuk menganalisis data jumlah kebutuhan BBM jenis Premium adalah

  • A.    Mecari Model Input

Plot time series untuk mencari gambaran umum tentang pola data. Berikut ini diagram plot time series data konsumsi premium bulan Januari 2009 sampai bulan Desember tahun 2013.

Plot Konsumsi Premium di Kota Denpasar (Jan. 2009 - Des. 2013)

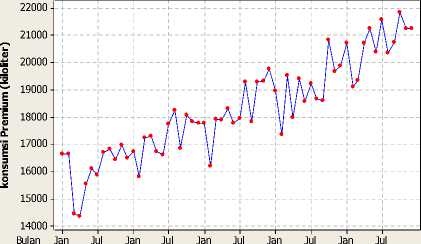
Tahun 2009        2010        2011         2012        2013

Gambar 3.1 Plot Data Time Series Konsumsi Premium di Kota Denpasar

Setelah mendapatkan pola data time series seperti yang ditunjukkan pada Gambar 3.1, bisa dilihat bahwa data menunjukkan ada pengaruh

trend dan ketidak-stasioner dikare-nakan data menyebar tidak seimbang (mean tidak konstan), untuk memperjelas apakah mean konstan atau tidak dan ada pengaruh trend, maka dibuat Plot Fungsi Autoco-rrelation, Plot Fungsi Partial Autocorrelation, dan Plot Analisis Trend seperti Gambar berikut:

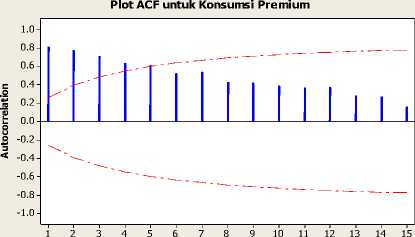
Lag

(a)

Plot PACF untuk Konsumsi Premium

1.0

0.8

■S

JS


m t £

0.6


0.4


0.0


0.2

-0.2


-0.4


-0.6


-0.8

-1.0

1    2    3    4    5    6    7    8    9    10   11   12   13   14   15

Lag

(b)

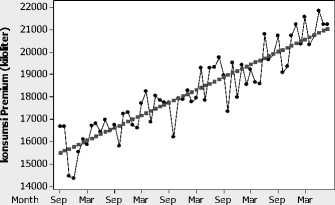
Trend Analysis Plot for konsumsi Premium (kiloliter) Linear Trend Model

Yt = 15394 + 94.4*t

Variable

—•— Actual ■ Fits

Accuracy Measures

MAPE       3

MAD      567

MSD   500779

Year 2014 2015      2016      2017      2018      2019

(c)

Gambar 3.2 (a). Plot Fungsi Autocorrelation, (b). Plot Fungsi Partial Autocorrelation, dan (c) Plot Analisis Trend

Gambar 3.2 (a) menunjukkan bahwa data belum stasioner terhadap mean, sedangkan (c), menunjukkan ada pengaruh trend yang linier pada data konsumsi premium Kota Denpasar.

Setelah mengetahui bahwa data belum stasioner, maka dilakukan differencing orde pertama untuk menstasionerkan data. Setelah differencing orde pertama pada data konsumsi premium Kota Denpasar dilakukan, diperoleh data yang sudah stasioner dalam mean, karena sudah menyebar seimbang (mean konstan). Plot data time series konsumsi premium Kota Denpasar yang telah didifferencing:

Plot Konsumsi Premium di Kota Denpasar (Jan. 2009 - Des. 2013) Difference Orde Pertama

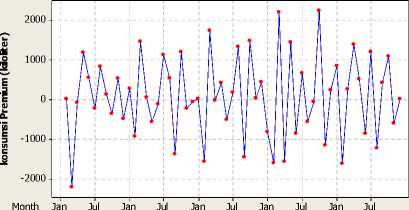
Year 2009         2010         2011         2012         2013

Gambar 3.3 Plot Time Series Differencing

Selanjutnya untuk mengetahui pola data sebenarnya, maka dibuat Plot Fungsi Autocorrelation, Plot Fungsi Partial Autocorrelation.

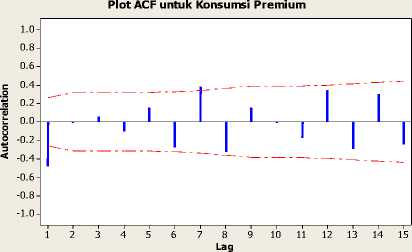
(a)

Partial Autocorrelation Function untuk Konsumsi Premium (with 5% significance limits for the partial autocorrelations)

2

1.0

0.8

0.6

0.4

0.2

0.0

t -0.4

£ -0.6

-0.8

-1.0

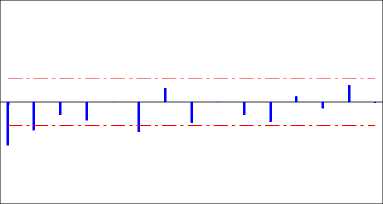
1    2    3    4   5    6    7   8    9   10   11   12   13   14   15

Lag

(b)

Gambar 3.4 (a) Plot ACF Data Differencing. dan (b) Plot PACF Data Differencing.

Gambar 3.4 memperlihatkan bahwa data jumlah konsumsi premium Kota Denpasar sudah stasioner dan pada plot PACF bisa dilihat bahwa dua lag pertama yang melebihi batas standar error yaitu lag 1, lag 2, dan lag 6 sehingga model input pada representasi algoritma genetika yang akan digunakan yaitu:

Tabel 3.1 Model Input algoritma Genetika

No

Model Input

1

%t — a o + & i Zt - i

2

Zt — ao + IiiZt _ i + a? Zt - 2

3

zt — do + IilZt _ i + «2 Zt - 2 + aZ Zt - 3

4

Zt — a O+ α i Zt _ i + α 2 Zt - 2 + α 3 Zt - 3 + a4Zt _ 4

5

zt — aO + iiizt _ i + α2 Zt _ 2 + α3 Zt - 3 + d4Zt _4 + aS Zt - S

6

zt — aO + aizt _ i + a2 Zt - 2 + a3 Zt - 3 + a4Zt_4 + aS Zt - S + d6Zt _ 6

7

zt — aO + aizt _ i + a2 Zt - 2 + a6Zt _ 6

8

Zt — ai Zt_ i + a2 Zt_2 + a3 Zt_ 3 + a4Zt _ 4

+ «S Zt _ S + dbzt - 6

  • B.    Tahap Pencarian Populasi dan Selang

Populasi Acak

Berdasarkan representasi kromosom yang telah dibentuk dari model input, data konsumsi premium Kota Denpasar kemudian diregresikan menggunakan masing-masing representasi kromosom untuk memperoleh populasi dan selang pembangkit populasi.

Regresi dilakukan dengan mengambil 30 data secara terurut menggunakan software microsoft excel, sehingga diperoleh 30 individu dari model input 1, 29 individu dari model input 2, 28 individu dari model input 3, 27 individu dari model input 4, 26 individu dari model input 5, dan 25 individu dari model input 6, 7, dan 8. Individu dari masing-masing model, dicari nilai minimum dan maksimum yang akan digunakan untuk membangkit individu lain yang mungkin belum muncul pada populasi hasil regresi.

  • C.    Pencarian Individu Terbaik

Peramalan dengan algoritma genetika ini menggunakan pengkodean real dengan simulasi program menggunakan software matlab R2012b. Pada tahap ini, masing-masing model kemudian dicari individu yang memiliki nilai fitness

terkecil, sehingga diperoleh delapan individu terbaik yang memiliki fitness terkecil.

Individu-individu tersebut kemudian dibandingkan satu sama lain sehingga diperoleh satu individu terbaik yang akan digunakan untuk peramalan data jumlah kebutuhan BBM jenis premium Kota Denpasar. Tahapan peramalan menggunakan algoritma genetika adalah sebagai berikut:

Inisialisasi Populasi Awal

Populasi yang telah dibentuk dari proses regresi kemudian ditambahkan dengan sejumlah populasi baru yang dibangkitkan secara acak dari selang nilai minimum dan maksimum, sehingga populasi awal yang diperoleh berjumlah 50 individu.

Evaluasi Nilai Fitness

Individu pada populasi yang telah diinisialisasi tadi, kemudian dihitung nilai fitnessnya dan diurutkan secara ascending berdasarkan nilai fitness. Setelah evaluasi fitness dilakukan, langkah selanjutnya adalah melakukan proses evolusi yaitu seleksi orang tua, crossover, mutasi, dan elitisme dengan pengulangan sebanyak generasi = 500.

Seleksi Orang Tua

Seleksi orang tua yang digunakan adalah seleksi steady state, metode ini dilakukan dengan cara mengambil individu terbaik sebagai orang tua sebanyak 50% (25 individu) dari populasi yang telah terurut. Kemudian individu yang terseleksi tersebut diinisialisasikan sebagai ortu(1), ortu(2) hingga ortu(25).

Crossover

Orang tua yang telah terpilih menggunakan metode steady state, kemudian dikawinsilangkan (crossover) dengan probabilitas crossover (Pcros) = 80% menggunakan metode arithmatic-crossover. Hasil dari proses crossover disebut sebagai offspring dan diinisialisasikan sebagai anak dan akan dimasukan ke dalam populasi, sehingga jumlah populasi akan bertambah.

Mutasi

Populasi yang telah bertambah sebelumnya akan dimutasi dengan probabilitas mutasi Pmut = 50%. Proses mutasi dilakukan dengan cara mengganti nilai gen (allele) pada locus yang memiliki probabilitas terpilih kurang dari Pmut dengan nilai acak pada selang [0,1] . Individu-individu yang mengalami mutasi, akan diinisialisasikan sebagai individu baru dan dimasukkan ke dalam populasi.

Elitisme dan Seleksi Populasi

Setelah proses seleksi orang tua, crossover,dan mutasi dilakukan, proses elistime dilakukan dengan cara menghitung nilai fitness individu dalam populasi dan diurutkan berdasarkan nilai fitnessnya secara ascending kemudian individu yang terpilih menjadi populasi selanjutnya adalah 50 individu terbaik pertama.

Individu Terbaik

Dari proses seleksi, crossover, mutasi, elitisme, dan seleksi populasi diperoleh individu terbaik yang memiliki nilai fitness terkecil, ditunjukkan pada tabel berikut ini:

Tabel 3.2 Individu Terbaik dari Kedelapan Model

Model Input

Individu

Fitness (MAE)

1

3108,1235 0,8303

773,4156

2

3253,4006 0,3933 0,4402

688,9503

3

1985,4837 0,2809 0,3722 0,2490

617,7826

4

2205,1063 0,2512 0,2818 0,1237 0,2407

571,2109

5

1689,2060 0,0997 0,2550 0,1996 0,2559

0,1221

562,5746

6

1071,6501 -0,0327 0,284 0,2361 0,2256 0,0540 0,1988

553,2560

7

2256,7735 0,1889 0,3638 0,3450

595,7843

8

-0,0244 0,2594 0,2496 0,1860 0,0854 0,2692

559,7168

Tabel 3.2 menunjukkan bahwa individu tebaik dengan fitness terkecil yaitu individu dari model input keenam, sehingga model peramalan yang diperoleh adalah:

̂t = 1071.6501 - 0.0327 ∗ Zt-i+0.284∗Zt-2 (3.1)

0.2361 ∗ Zt-3 + 0.2256 ∗ Zt-4+0.054∗Zt-S

+0.1988 ∗ Zt-6

Persamaan (3.1) akan digunakan untuk meramalkan jumlah kebutuhan BBM jenis premium Kota Denpasar periode Bulan Januari 2014 hingga Juni 2014.

  • D.    Peramalan In-sample Jumlah Konsumsi

Premium

Grafik peramalan in-sample jumlah kebutuhan BBM jenis premium dapat dilihat pada Gambar berikut:

21500

20500

19500

18500

17500

16500

15500

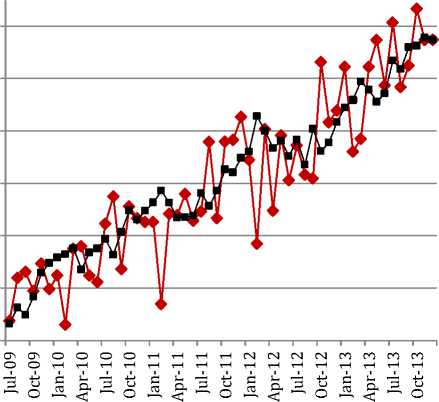
—∙— Data Konsumsi Premium Kota Denpasar

—■— Data Ramalan Konsumsi Premium Kota Denpasar


Gambar 3.5 Peramalan Jumlah Kebutuhan Premium Kota Denpasar Tahun 2013

Gambar 3.5 merupakan grafik uji model linier untuk peramalan in-sample jumlah kebutuhan premium di Kota Denpasar MAE = 553,2690 kiloliter dan MAPE = 3,0217%.

  • E.    Peramalan Out of Sample Jumlah Konsumsi Premium

Grafik hasil peramalan jumlah konsumsi premium Kota Denpasar Bulan Januari hingga Juni tahun 2014 dapat dilihat pada Gambar 3.6 sebagai berikut:

Data Ramalan Jumlah Kebutuhan Premium

Periode Januari hingga Juni Tahun 2014

22000

21800

21600

21400

21200

21000


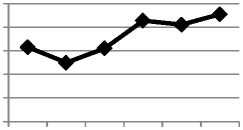
Data Ramalan Konsumsi Premium

Gambar 3.6 Peramalan Out of Sample Jumlah Kebutuhan Premium Kota Denpasar

Gambar 3.6 menunjukkan bahwa jumlah konsumsi premium di Kota Denpasar mengalami flukstuasi dengan rata-rata jumlah kebutuhan premium Kota Denpasar sebesar 21722,85935 kiloliter. Hasil peramalan menunjukkan bahwa jumlah konsumsi premium terbesar di Kota Denpasar terjadi pada Bulan Juni 2014 yaitu 21910,3237 kiloliter dan jumlah konsumsi premium terendah terjadi pada bulan Pebruari 2014 yaitu 21499,2790 kiloliter.

  • 4.    SIMPULAN DAN REKOMENDASI

  • A.    Simpulan Penelitian

Berdasarkan hasil yang telah diperoleh pada kasus peramalan jumlah kebutuhan premium

tahun 2014, maka dapat ditarik kesimpulan bahwa:

Kinerja algoritma genetika dalam meramalkan jumlah kebutuhan BBM jenis premium di Kota Denpasar cukup baik dengan nilai error yang dihasilkan yaitu MAE sebesar 553,2690 dan MAPE sebesar 3.0217%.

Penggunaan BBM jenis premium di Kota Denpasar, mengalami fluktuasi dengan rata-rata jumlah kebutuhan premium    sebesar

21722,85935 kiloliter.

  • B.    Rekomendasi

Dari simpulan di atas akan disampaikan beberapa saran yang dapat dijadikan pertimbangan, saran tersebut antara lain:

  • 1.    Algoritma genetika pada penelitian ini menggunakan pengkodean    real,

sehingga mungkin untuk penelitian lebih lanjut dapat menggunakan pengkodean biner.

  • 2.    Melakukan perbandingan metode peramalan menggunakan algoritma genetika dengan metode peramalan yang lain.

DAFTAR PUSTAKA

  • [1]    Patria, D.P.N., 2009. "Penerapan Algoritma Genetika Dalam Pencarian Nilai Parameter Untuk Peramalan Data Penjualan Secara Time Series". Skripsi. Malang: Universitas Brawijaya.

  • [2]    Suyanto. 2011. Artificial Intelligence (Searching-Reasoning-Planning-Learning).

Edisi revisi. Bandung: Informatika.

  • [3]    Utari, P.D., 2011. “Prediksi Permintaan

BBM Di PT. Pertamina Region V Dengan Metode Peramalan Data Time Series Hirarki”. Jurnal FMIPA-ITS. Surabaya: Institut Teknologi Sepuluh November.

LAMPIRAN

Output Program Peramalan In-sample

Z(t-6)Z(t-5)Z(t-4)Z(t-3)Z(t-2)Z(t-1) z(t)    z duga    error

16656

16656 14448

14360

15544

16096

15872 15820.3085

51.6915

16656

14448 14360

15544

16096

15872

16696 16124.8589

571.1411

14448

14360 15544

16096

15872

16696

16808 15988.0333

819.9667

14360

15544 16096

15872

16696

16808

16440 16336.4733

103.5267

15544

16096 15872

16696

16808

16440

16968 16789.5141

178.4859

16096

15872 16696

16808

16440

16968

16480 16977.7157

497.7157

15872

16696 16808

16440

16968

16480

16744 17081.9725

337.9725

16696

16808 16440

16968

16480

16744

15800 17146.2469

1346.2469

16808

16440 16968

16480

16744

15800

17248 17258.3853

10.3853

16440

16968 16480

16744

15800

17248

17296 16850.5309

445.4691

16968

16480 16744

15800

17248

17296

16736 17175.4877

439.4877

16480

16744 15800

17248

17296

16736

16616 17253.5797

637.5797

16744

15800 17248

17296

16736

16616

17728 17437.9725

290.0275

15800

17248 17296

16736

16616

17728

18248 17136.6677

1111.3323

17248

17296 16736

16616

17728

18248

16864 17571.2581

707.2581

17296

16736 16616

17728

18248

16864

18056 17978.9685

77.0315

16736

16616 17728

18248

16864

18056

17832 17802.7653

29.2347

16616

17728 18248

16864

18056

17832

17760 17975.3597

215.3597

17728

18248 16864

18056

17832

17760

17760 18132.4445

372.4445

18248

16864 18056

17832

17760

17760

16192 18356.6653

2164.6653

16864

18056 17832

17760

17760

16192

17720 18129.6341

409.6341

18056

17832 17760

17760

16192

17720

17888 17842.9869

45.0131

17832

17760 17760

16192

17720

17888

18296 17852.8213

443.1787

17760

17760 16192

17720

17888

18296

17784 17879.8981

95.8981

17760

16192 17720

17888

18296

17784

17960 18312.2221

352.2221

16192

17720 17888

18296

17784

17960

19288 18066.0821

1221.9179

17720

17888 18296

17784

17960

19288

17832 18356.6405

524.6405

17888

18296 17784

17960

19288

17832

19296 18762.8805

533.1195

18296

17784 17960

19288

17832

19296

19328 18708.2125

619.7875

17784

17960 19288

17832

19296

19328

19768 18986.4957

781.5043

17960

19288 17832

19296

19328

19768

18944 19105.0733

161.0733

19288

17832 19296

19328

19768

18944

17344 19780.1941

2436.1941

17832

19296 19328

19768

18944

17344

19536 19499.2045

36.7955

19296

19328 19768

18944

17344

19536

17976 19170.6149

1194.6149

19328

19768 18944

17344

19536

17976

19416 19310.6221

105.3779

19768

18944 17344

19536

17976

19416

18560 19020.0413

460.0413

18944

17344 19536

17976

19416

18560

19224 19332.9805

108.9805

17344

19536 17976

19416

18560

19224

18664 18856.4997

192.4997

19536

17976 19416

18560

19224

18664

18592 19537.6797

945.6797

17976

19416 18560

19224

18664

18592

20816 19112.2829

1703.7171

19416

18560 19224

18664

18592

20816

19664 19276.7405

387.2595

18560

19224 18664

18592

20816

19664

19888 19668.3749

219.6251

19224

18664 18592

20816

19664

19888

20722 19944.4885

777.5115

18664

18592 20816

19664

19888

20722

19106 20095.3639

989.3639

18592

20816 19664

19888

20722

19106

19346 20283.8407

937.8407

20816

19664 19888

20722

19106

19346

20722 20444.4137

277.5863

19664

19888 20722

19106

19346

20722

21234 20057.2697

1176.7303

19888

20722 19106

19346

20722

21234

20370 20212.9729

157.0271

20722

19106 19346

20722

21234

20370

21570 20844.1865

725.8135

19106

19346 20722

21234

20370

21570

20338 20682.5785

344.5785

19346

20722 21234

20370

21570

20338

20746 21097.1977

351.1977

20722

21234 20370

21570

20338

20746

21834 21123.5665

710.4335

21234

20370 21570

20338

20746

21834

21236 21238.8353

2.8353

20370

21570 20338

20746

21834

21236

21239 21278.8083

39.8083

MAE  = 553.2690

MAPE =   3.0217 persen

Output Program Peramalan Out-sample

Bulan

Data Duga

1-2014

21629.8318

2-2014

21499.2790

3-2014

21620.2062

4-2014

21856.1295

5-2014

21821.3859

6-2014

21910.3237

Total

130337.1561

Minimum

21499.2790

Maksimum

21910.3237

Rata-rata

21722.85935

167