PENGELOMPOKKAN KABUPATEN DI PROVINSI JAWA TENGAH BERDASARKAN KARAKTERISTIK IKLIM MENGGUNAKAN FUZZY CLUSTERING
on
E-Jurnal Matematika Vol. 13(1), Januari 2024, pp. 57-65
DOI: https://doi.org/10.24843/MTK.2024.v13.i01.p442
ISSN: 2303-1751
PENGELOMPOKKAN KABUPATEN DI PROVINSI JAWA TENGAH BERDASARKAN KARAKTERISTIK IKLIM MENGGUNAKAN FUZZY CLUSTERING
Natalie Novenrodumetasa1§, G. K. Gandhiadi2, Ketut Jayanegara3
1Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: natameta28@gmail.com] 2Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: gandhiadi@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: ktjayanegara@unud.ac.id]
§Corresponding Author
ABSTRACT
There are many factors affecting human life, one of which is climate. Differences in climatic conditions in each region result in differences in the environment in society. The differences are referred to as potential natural resources, livelihoods, and social cultural conditions. The climate has an impact on culture in terms of how people dress, the shape of houses, and so on. The regency group in Central Java Province is based on similarities in climate characteristics using fuzzy clustering. The data used were taken from Central Java Provincial Statistical Office in 2022.The results of district grouping in Central Java Province are based on similarities in climate characteristics using fuzzy clustering with 4 different number of clusters and the validity tests of the Partition Coefficient and Classification Entropy indices. Based on the results of the index validity test, the optimal grouping results are 2 clusters with a Partition Coefficient value of 0.911233 and a Classification Entropy value of 0.07979. The 1st cluster consists of 13 districts with a cluster center at 27.9°C for air temperature, 2418mm for rainfall, and 804% for keelThe 2nd cluster and airbase consist of 22 cluster central districts at 26.6 °C for air temperature, 4087 mm for rainfall, and 81.3% for humidity.
Keywords: Fuzzy, Clustering, Climate
dengan curah hujan, suhu serta tekanan udara, juga faktor meteorologi lainnya disebut iklim (Tjasyono, 2004). Karakteristik iklim suatu daerah ditentukan oleh probabilitas beberapa indikator yang ditetapkan, seperti suhu, curah hujan, dan kelembaban udara.
Suhu udara adalah salah satu faktor iklim yang penting. Tinggi rendahnya suhu bisa berubah sewaktu-waktu berdasarkan lokasi serta waktunya (Tjasyono, 1992). Curah hujan merupakan kuantitas air hujan jatuh di satu wilayah pada satu kurun waktu. Terjadinya kondensasi uap air yang dibawa angin dapat membentuk sebuah awan yang dapat menyebabkan curah hujan menyebar ke seluruh wilayah (Lakitan,2002). Menurut Nasir, dkk.,(2017) kelembaban udara adalah konsentrasi uap air yang ada di dalam udara. Jumlah tersebut sesungguhnya merupakan sedikit dari keseluruhan atmosfer.
Ginting (2017) melakukan pengelompokkan kabupaten atau kota yang
terletak di Provinsi Sumatera Utara berdasarkan karakteristik iklim dengan menggunakan Metode Ward dan Metode Average Linkage. Penelitian Ginting (2017) mendapatkan hasil 4 cluster berdasarkan karateristik iklim yaitu cluster 1 terdiri dari kabupaten/kota yang memiliki nilai pusat untuk curah hujan dan penguapan yang tinggi, cluster 2 terdiri dari kabupaten/kota dengan nilai centroid yang tinggi untuk penguapan dan suhu, cluster 3 terdiri dari kabupaten/kota dengan tingkat penyinaran yang lebih dominan namun tidak terlalu tinggi dan tingkat suhu yang tidak tinggi, cluster 4 terdiri dari kabupaten/kota dengan nilai centroid yang tinggi untuk penyinaran matahari.
Selanjutnya, Juaeni,dkk (2010) melakukan pengelompokkan wilayah curah hujan di Kalimantan Barat berbasis Metode Ward dan Fuzzy Clustering. Pada penelitian ini menghasilkan 4 kelompok grid yang memiliki karakteristik curah hujan yang homogen. Perbedaan jumlah grid antar cluster antara metode Ward dan metode Fuzzy Clustering disebabkan oleh adanya penerapan overlapping pada metode Fuzzy, sehingga menyebabkan grid tertentu bisa menjadi anggota di dua cluster atau lebih dengan nilai derajat keanggotaan yang berbeda. Metode Fuzzy Clustering menunjukkan hasil pembandingan intensitas curah hujan yang lebih baik dibandingkan metode Ward pada panelitian tersebut. Berdasarkan penelitian terdahulu, peneliti akan melakukan pengelompokkan kabuapten di Provinsi Jawa Tengah berdasarkan karakteristik iklim menggunakan Fuzzy Clustering.
Fuzzy sendiri memiliki arti samar atau ketidakjelasan yang dapat memiliki nilai benar dan salah secara bersamaan. Konsep logika fuzzy dikembangkan oleh Lotfi A. Zadeh pada tahun 1965 sebagai alternatif untuk logika biner tradisional yang hanya mengenal nilai kebenaran "benar" atau "salah". Logika fuzzy memungkinkan penggunaan derajat kebenaran yang lebih fleksibel, yang dapat berada di antara nilai "benar" dan "salah" dengan menggunakan konsep keanggotaan pada himpunan. Dalam menggunakan logika fuzzy, nilai kebnenaran yang dihasilkan bukan hanya 0 atau 1, melainkan semua kemungkinan antara 0 dan 1, yang mencerminkan sejauh mana suatu pernyataan benar (Kusumadewi & Purnomo, 2013.
Clustering adalah metode pengelompokkan data. Menurut Tan et al. (2006) clustering adalah proses untuk mengelompokkan data ke dalam beberapa cluster atau kelompok sehingga data dalam satu cluster memiliki tingkat kemiripan yang maksimum dan data antar cluster memiliki kemiripan yang minimum. Clustering yang menghasilkan tingkat kemiripan yang tinggi didalam satu cluster dan tingkat kemiripan yang rendah antar cluster merupakan hasil yang baik. Metode paling umum yang digunakan untuk menghitung jarak antar objek salah satunya adalah Jarak Euclidean.
Fuzzy clustering adalah salah satu cara dalam penentuan cluster optimal dalam suatu ruang vektor yang didasarkan pada bentuk normal Euclidean untuk jarak antar vektor. Ada beberapa algoritma clustering data, salah satunya adalah Fuzzy C-Means (FCM). FCM adalah suatu teknik pengclusteran data yang mana keberadaan tiap-tiap data dalam suatu cluster ditentukan oleh derajat keanggotaan. Metode ini pertama kali diperkenalkan oleh Jim Bezdek pada tahun 1981 (Kusumadewi & Purnomo, 2013). Prinsip utama dalam melakukan pengelompokkan dengan FCM adalah mendapatkan nilai fungsi objektif paling minimum (Shihab, 2000)
Jfcm(P,U,X,c,m) = ∑i=1∑%=1(μil∂md2k(x^
dengan asumsi harus memenuhi ketentuan sebagai berikut:
C
∑ μik = 1,untiik. ∀k ∈ {1, ..,n} 1=1
Dengan c adalah umlah cluster, m adalah tingkat ke-fuzzy-an (fuzzier), μik adalah nilai derajat keanggotaan, n adalah jumlah data, d2k adalah ukuran jarak antara data dengan pusat cluster.
-
2. METODE PENELITIAN
-
a. Jenis dan Sumber Data
Data yang digunakan pada penelitian ini adalah data sekunder. Sumber data diambil dari data Indikator Iklim di 29 kabupaten dan 6 kota Provinsi Jawa Tengah Badan Pusat Statistik Provinsi Jawa Tengah Tahun 2022.
-
b. Variabel Penelitian
Adapun variabel yang digunakan dalam penelitian ini adalah sebagai berikut:
-
1. %1 : Rata-rata bulanan suhu udara
DOI: https://doi.org/10.24843/MTK.2024.v13.i01.p442
-
2. %2 : Rata-rata bulanan curah hujan
-
3. X3 : Rata-rata bulanan kelembaban udara
-
c. Analisis Data
Tahapan Analisis data menggunakan algoritma Fuzzy C-Means adalah sebagai berikut:
-
1. Memasukkan data yang akan dicluster X, berupa matriks berukuran n × m, dimana n = jumlah kabupaten dan m = jumlah atribut data
-
2. Menentukan jumlah cluster (c), jumlah cluster yang akan dibentuk adalah 2 sampai 5 cluster.
-
3. Menentukan parameter awal lainnya, pangkat pembobot (w), maksimum iterasi (MaxIter), error terkecil yang diharapkan (.0, fungsi obyektif awal (P0) dan iterasi awal (t).
-
4. Membangkitkan bilangan random μik sebagai elemen-elemen matriks partisi awal U seperti pada persamaan
-
5. Menghitung pusat cluster Vkj dari setiap cluster yang akan dibentuk dengan persamaan
-
6. Menghitung fungsi obyektif Pt dengan persamaan
-
7. Memperbaiki nilai μtk pada matriks partisi U dengan persamaan
-
8. Mengecek kondisi berhenti:
-
a. Jika: ( |Pt — Pt-1∣ < .) atau (t >
MaxIter) maka berhenti;
-
b. Jika tidak: t = t+1, ulangi langkah ke-4 dengan menggunakan matriks partisi yang sudah diperbaharui
-
9. Mengukur validitas cluster yang didapatkan dengan uji validitas cluster.
-
10. Melakukan interpretasi hasil cluster yang didapatkan.
-
3. HASIL DAN PEMBAHASAN
-
a. Fuzzy Clustering
Pengelompokkan fuzzy clustering ini dilakukan menggunakan algoritma fuzzy c-means. Pada penelitian ini akan menggunakan 3 atribut karakteristik iklim, yaitu suhu udara, curah hujan, dan kelembaban udara.
Langkah-langkah perhitungan untuk
melakukan pengelompokkan menggunakan algoritma fuzzy c-means adalah sebagai berikut:
-
1. Input data
Menginput data yang akan dicluster X, berupa matriks berukuran n×m (n = jumlah sampel data, m = jumlah atribut data). xij = data sampel ke-i (i=1,2,...,35), atribut ke-j (j=1,2,3).
|
■ 27,2 |
4661 |
82,0' | |
|
^35X3 — |
27,8 |
4161 |
81,0 |
|
. 27,9 |
2225 |
8(),0. |
-
2. Menentukan parameter awal
Menentukan parameter awal yang akan digunakan yaitu, jumlah cluster, pangkat pemobot, maksimum iterasi, error terkecil, fungsi objektif awal, dan iterasi awal.
Tabel 1. Parameter Awal
|
Parameter awal |
Keterangan |
|
Jumlah cluster |
2,3,4,5 |
|
Pangkat pembobot |
2 |
|
Maksimum iterasi |
100 |
|
Error terkecil |
0,00001 |
|
Fungsi Objektif awal |
0 |
|
Iterasi awal |
1 |
-
3. Membangkitkan matriks partisi awal
Sesudah menetapkan parameter awal yang digunakan, selanjutnya membangkitkan bilangan random berupa matriks yang sesuai dengan jumlah data dan cluster yang akan digunakan.
|
0,3434 |
0,6566-1 | |
|
0,5152 |
0,4848 | |
|
0,6263 |
0,3737 | |
|
0,2121 |
0,7879 | |
|
0,4343 |
0,5657 | |
|
0,2424 |
0,7576 | |
|
U35×2 — |
0,7374 |
0,2626 |
|
⋮ 0,4548 |
⋮ 0,5452 | |
|
0,5178 |
0,4822 | |
|
0,5423 |
0,4577 | |
|
0,7766 |
0,2234 | |
|
.0,1212 |
0,8788. |
-
4. Mengitung Pusat cluster
Sesudah mendapatkan matriks partisi awal U, selanjutnya akan dihitung pusat cluster untuk masing-masing cluster.
τr _ ∑i=5ι((Mtfe )*^tj)
Vkj = ∑LW
Contoh:
τr __ ∑t=5ι((fiik ')tχij)
V11 = V3S 2
∑1=1 ∣j-ιk
[(0,34342x27,2) + - + (0,12122×27,9)] [0,34342+0,51522 + -+0,77662+0,12122]
_ 285,9231 _ „„„ ^^/ , ι3 8,5114
Pada tabel 2 telah didapatkan hasil perhitungan pusat cluster untuk setiap cluster sementara
Tabel 2. Pusat Cluster Awal
|
Cluster |
Suhu Udara (0C) |
Curah Hujan (mm) |
Kelembaban Udara (%) |
|
1 |
27,9 |
2418 |
80,4 |
|
2 |
26,6 |
4087 |
81,3 |
-
5. Menghitung Fungsi Objektif
Sesudah mendapatkan pusat cluster untuk masing-masing cluster pada setiap variabel, selanjutnya akan dihitung fungsi objektif.
Pt = ∑351∑L1 ([∑3=1(¾∙ - ¾')2] (‰)2) P1 = ∑3=1([(27,2 - 27,3)2 + (4661 -2994)2 + (82 - 80,6)2 × (0,3434)2] + [(27,2 - 27,5)2 + (4661 - 3140)2 + (82 - 80,8)2 × (0,6566)2])
P1 = 16219049,847316
diperbaharui. Pada penelitian ini iterasi berhenti pada iterasi ke-13 dengan nilai pusat cluster akhir pada Tabel 3.
Tabel 3. Pusat Cluster Akhir
|
Cluster |
Suhu Udara (°C) |
Curah Hujan (mm) |
Kelembaban Udara (%) |
|
1 |
27,3 |
2994 |
80,6 |
|
2 |
27,4 |
3140 |
80,8 |
|
Data ke- |
Pn |
Pi2 |
Data masuk cluster ke- |
|
1 |
0.9386 |
0.0614 |
1 |
|
2 |
0.9982 |
0.0018 |
1 |
|
3 |
0.9953 |
0.0047 |
1 |
|
30 |
0.9982 |
0.0018 |
1 |
|
31 |
0.1033 |
0.8967 |
2 |
|
32 |
0.3765 |
0.6235 |
2 |
|
33 |
0.0287 |
0.9713 |
2 |
|
34 |
0.0022 |
0.9978 |
2 |
|
35 |
0.0106 |
0.9894 |
2 |
-
6. Menghitung perubahan matriks partisi
Setelah mendapatkan nilai fungsi objektif, selanjutnya akan dilakukan perhitungan perubahan nilai untuk μik yang baru. -1
[∑‰(¾-¼∙)2]2-1 μ⅛ =—ξt ∑⅛=ι([∑3=ι(χi7-yk7∙)2])2-1
Contoh:
⅛1 =
__________________((27,2-27,3)2+-+(82-80,6)2)~1__________________ ((27,2-27,3)2 + -+(82-80,6)2)-1+((27,2-27,4)2 + -+(82-80,8)2)-1
Nilai derajat keanggotaan terakhir dapat dilihat pada tabel 4.
Tabel 4. Nilai Derajat Keanggotaan untuk Jumlah 2 Cluster
Pada Tabel 4 didapatkan nilai derajat keanggotaan akhir untuk setiap data. Penetuan suatu data masuk kedalam cluster 1 atau 2 ditentukan dengan cara membandingkan nilai derajat keanggotaannya dalam cluster 1 atau 2 dan data akan masuk kedalam cluster dengan nilai derajat keanggotaan yang lebih tinggi.
_ 2778485,8949 5091660,7783
7. Mengecek kondisi berhenti
Setelah mendapatkan hasil perhitungan nilai fungsi objektif dan matriks partisi baru, selanjutnya akan melakukan pengecekan kondisi berhenti dengan cara melakukan pengurangan nilai antar fungsi objektif. Pada perhitungan yang telah dilakukan pada iterasi pertama diperoleh nilai fungsi objektif P1 sebesar 16219049,847316 sehingga ( ∣P1 - P0| > O atau iterasi = 1 < MaxIter (=100), maka proses dilanjutkan ke iterasi ke-2 (t=2). Perhitungan iterasi ke-2 menggunakan matriks partisi yang sudah
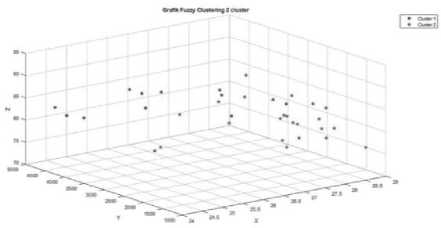
Gambar 1. Grafik Fungsi Clustering untuk Jumlah 2 Cluster
Pada gambar 1 dapat dilihat grafik hasil pengelompokkan dengan jumlah 2 cluster berdasarkan karakteristik iklim. Hasil pengelompokan yang didapatkan adalah 13 kabupaten/ kota (Cilacap, Kab. Banyumas,
Kab. Purbalingga, Kab. Banjarnegara, Kab. Kebumen, Kab. Purworejo, Kab. Wonosobo, Kab. Magelang, Kab. Sukoharjo, Kab. Demak, Kab. Semarang, Kab. Pekalongan dan Kota Magelang) berada di cluster 1 yang berwarna biru dan 22 kabupaten/kota (Kab. Boyolali, Kab. Klaten, Kab. Wonogiri, Kab. Karanganyar, Kab. Sragen, Kab. Grobogan, Kab. Blora, Kab. Rembang, Kab. Pati, Kab. Kudus, Kab. Jepara, Kab. Temanggung, Kab. Kendal, Kab. Batang, Kab. Pemalang, Kab. Tegal, Kab. Brebes, Kota Surakarta, Kota Salatiga, Kota Semarang, Kota Pekalongan, dan Kota Tegal) berada di cluster 2 yang berwarna merah.
-
b. Fuzzy Clustering Menggunakan Matlab
Pada pengujian sebelumnya telah dilakukan untuk parameter jumlah cluster 2. Pengelompokkan untuk parameter jumlah cluster 3, 4, dan 5 akan dilakukan menggunakan bantuan software matlab.
Untuk melakukan pengujian dengan matlab, data yang digunakan terlebih dahulu diimport kedalam matlab.
iklim 1
ffl 35x3 double
|
1 |
2 |
3 |
4 | |
|
V |
4661 |
82 | ||
|
2 |
2B |
4161 |
81 | |
|
3 |
28 |
4210 |
82 | |
|
4 |
24 |
4250 |
85 | |
|
5 |
26 |
4431 |
85 | |
|
6 |
29 |
3890 |
79 | |
|
7 |
24 |
3953 |
84 | |
|
8 |
26 |
4116 |
85 | |
|
9 |
28 |
2568 |
81 | |
|
10 |
29 |
2712 |
78 | |
|
11 |
29 |
3550 |
79 | |
|
12 |
27 |
2494 |
92 | |
|
13 |
27 |
2529 |
87 | |
|
14 |
29 |
2534 |
81 | |
|
15 |
29 |
2324 | ||
|
16 |
29 |
1517 |
75 | |
|
17 |
29 |
2868 |
81 | |
|
IR |
28 |
2181 |
77 |
Gambar 2. Import Data
Setelah data sudah diinput kedalam matlab, akan digunakan source code dengan menambahkan fungsi FCM (Fuzzy C-Means) untuk mendapatkan hasil pengelompokkannya.
-
1. Pengujian untuk jumlah cluster 3
Hasil pertama yang didapatkan adalah jumlah iterasi dan hasil perhitungan fungsi objektif.
Tabel 5. Jumlah Iterasi dan Nilai Fungsi Objektif untuk Jumlah 3 Cluster
Iterasi ke- Nilai Fungsi Objektif
|
1 |
11611269.405811 |
|
2 |
8108964.383991 |
|
39 |
2080465.243437 |
|
40 |
2080465.243409 |
Pada Tabel 5 terdapat jumlah iterasi dan hasil perhitungan fungsi objektif untuk pengelompokkan dengan parameter jumlah cluster 3. Pada perhitungan ini memerlukan iterasi sebanyak 40 kali untuk mencapai kondisi yang optimal.
Hasil kedua yang didapatkan hasil perhitungan nilai pusat cluster Vkj untuk setiap cluster pada masing-masing variabel yang dapat dilihat pada tabel 6.
Tabel 6. Pusat Cluster untuk Jumlah 3 Cluster
|
Cluster |
Suhu Udara (0C) |
Curah Hujan (mm) |
Kelembaban Udara (%) |
|
1 |
28,0 |
1569,8 |
78,1 |
|
2 |
26,5 |
4121,2 |
81,3 |
|
3 |
27,8 |
1584,3 |
80,9 |
Hasil ketiga yang didapatkan hasil perhitungan nilai matriks partisi baru U yang akan digunakan sebagai penentu suatu lebih cenderung data masuk kedalam satu cluster dengan nilai U paling tinggi diantara cluster lainnya.
Tabel 7. Nilai Derajat Keanggotaan untuk Jumlah 3
Cluster
|
Data ke- |
1 |
2 |
3 |
Data masuk cluster ke- |
|
1 |
0,0278 |
0,9107 |
0,0615 |
2 |
|
2 |
0,0002 |
0,9991 |
0,0006 |
2 |
|
3 |
0,0011 |
0,9959 |
0,0059 |
2 |
|
34 |
0,0943 |
0,0173 |
0,8884 |
3 |
|
35 |
0,2250 |
0,0269 |
0,7481 |
3 |
Pada tabel 7 didapatkan nilai derajat keanggotaan akhir untuk setiap data. Penetuan suatu data masuk kedalam cluster ditentukan dengan cara membandingkan nilai derajat keanggotaannya dalam cluster tersebut dan data akan masuk kedalam cluster dengan nilai

Gambar 3. Grafik fungsi clustering untuk jumlah 3 cluster
derajat keanggotaan yang lebih tinggi.
Pada Gambar 3 dapat dilihat grafik hasil pengelompokkan dengan jumlah 3 cluster, hasil pengelompokan yang didapatkan adalah 3 kabupaten (Kabupaten Blora, Kabupaten Pemalang, dan Kota Surakarta) berada di cluster 1 yang berwarna biru, 13 kabupaten (Kab. Cilacap, Kab. Banyumas, Kab. Purbalingga, Kab. Banjarnegara, Kab. Kebumen, Kab. Purworejo, Kab. Wonosobo, Kab. Magelang, Kab. Sukoharjo, Kab. Demak, Kab. Semarang, Kab. Pekalongan, dan Kota Magelang) berada di cluster 2 yang berwarna merah dan 19 kabupaten (Kab. Boyolali, Kab. Klaten, Kab. Wonogiri, Kab. Karanganyar, Kab. Sragen, Kab. Grobogan, Kab. Rembang, Kab. Pati, Kab. Kudus, Kab. Jepara, Kab. Temanggung, Kab. Kendal, Kab. Batang, Kab. Tegal, Kab. Brebes, Kota Salatiga, Kota Semarang, Kota Pekalongan, dan Kota Tegal) berada di cluster 3 yang berwarna oranye 1. Pengujian untuk jumlah cluster 4
Hasil pertama yang didapatkan adalah jumlah iterasi dan hasil perhitungan fungsi objektif.
Tabel 8. Jumlah Iterasi dan Nilai Fungsi Objektif untuk Jumlah 4 Cluster
|
Iterasi ke- |
Nilai Fungsi Objektif |
|
1 |
8474956,395320 |
|
2 |
5555633,731644 |
|
52 |
1210100,796314 |
|
53 |
1210100,796307 |
Pada Tabel 8 terdapat jumlah iterasi dan hasil perhitungan fungsi objektif untuk pengelompokkan dengan parameter jumlah cluster 4. Pada perhitungan ini memerlukan iterasi sebanyak 53 kali untuk mencapai kondisi yang optimal.
Hasil kedua yang didapatkan hasil perhitungan nilai pusat cluster Vkj untuk setiap cluster pada masing-masing variabel yang dapat dilihat pada tabel 9.
Tabel 9. Pusat Cluster untuk Jumlah 4 Cluster
|
Cluster |
Suhu Udara (0C) |
Curah Hujan (mm) |
Kelembaban Udara (%) |
|
1 |
26,2 |
4352,6 |
82,8 |
|
2 |
27,0 |
3815,7 |
79,0 |
|
3 |
28,0 |
11549,2 |
78,0 |
|
4 |
27,9 |
2547,5 |
80,8 |
Hasil ketiga yang didapatkan hasil perhitungan nilai matriks partisi baru U yang akan digunakan sebagai penentu suatu lebih cenderung data masuk kedalam satu cluster dengan nilai U paling tinggi diantara cluster lainnya.
Tabel 10. Nilai Derajat Kanggotaan untuk Jumlah 4
Cluster
|
Data ke- |
1 |
2 |
3 |
4 |
|
1 |
0,8589 |
0,1143 |
0,0084 |
0,0183 |
|
2 |
0,7535 |
0,2391 |
0,0041 |
0,0106 |
|
3 |
0,8765 |
0,1146 |
0,0025 |
0,0064 |
|
34 |
0,0000 |
0,0000 |
0,9998 |
0,0001 |
|
35 |
0,1130 |
0,3679 |
0,0642 |
4548 |
Pada Tabel 10 didapatkan nilai derajat keanggotaan akhir untuk setiap data. Penetuan suatu data masuk kedalam cluster ditentukan dengan cara membandingkan nilai derajat keanggotaannya dalam cluster tersebut dan data akan masuk kedalam cluster dengan nilai derajat keanggotaan yang lebih tinggi.
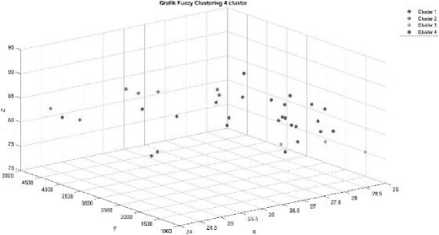
Gambar 4. Grafik Fungsi Clustering untuk Jumlah 4 Cluster
Pada gambar 4 dapat dilihat grafik hasil pengelompokkan dengan jumlah 4 cluster, hasil pengelompokan yang didapatkan adalah 7 kabupaten (Kab. Cilacap, Kab. Banyumas, Kab. Purbalingga, Kab. Banjarnegara, Kab. Kebumen, Kab. Magelang, dan Kab. Semarang) berada di cluster 1 yang berwarna biru, 7 kabupaten (Kab. Purworejo, Kab. Wonosobo, Kab. Sukoharjo, Kab. Demak, Kab. Temanggung, Kab. Pekalongan, dan Kota Magelang) berada di cluster 2 yang berwarna merah, 3 kabupaten (Kab. Blora, Kab. Pemalang, dan Kota Surakarta) berada di cluster 3 yang berwarna oranye, dan 18 kabupaten (Kab. Boyolali, Kab. Klaten, Kab. Wonogiri, Kab. Karanganyar, Kab. Sragen,
Kab. Grobogan, Kab. Rembang, Kab. Pati, Kab. Kudus, Kab. Jepara, Kab. Kendal, Kab. Batang, Kab. Tegal, Kab. Brebes, Kota Salatiga, Kota Semarang, Kota Pekalongan, dan Kota Tegal) berada di cluster 4 yang berwarna ungu.
-
2. Pengujian untuk jumlah cluster 5
Hasil pertama yang didapatkan adalah jumlah iterasi dan hasil perhitungan fungsi objektif.
Tabel 11. Jumlah Iterasi dan Nilai Fungsi Objektif untuk Jumlah 5 Cluster
|
Iterasi ke- |
Nilai Fungsi Objektif |
|
1 |
7296376,187026 |
|
2 |
4857704,986150 |
|
49 |
618385.777899 |
|
50 |
618385,777893 |
Pada Tabel 11 terdapat jumlah iterasi dan hasil perhitungan fungsi objektif untuk pengelompokkan dengan parameter jumlah cluster 5. Pada perhitungan ini memerlukan iterasi sebanyak 50 kali untuk mencapai kondisi yang optimal.
Hasil kedua yang didapatkan hasil perhitungan nilai pusat cluster Vkj untuk setiap cluster pada masing-masing variabel yang dapat dilihat pada Tabel 12.
Tabel 12. Pusat Cluster untuk Jumlah 5 Cluster
|
Cluster |
Suhu Udara (0C) |
Curah Hujan (mm) |
Kelembaban Udara (%) | |
|
1 |
27,9 |
2477,7 |
81,1 | |
|
2 |
27,3 |
3040,9 |
81,8 | |
|
3 |
25,9 |
4481,0 |
82,6 | |
|
4 |
26,7 |
3962,8 |
80,3 | |
|
5 |
28,0 |
1528,9 |
78,0 | |
Hasil ketiga yang didapatkan hasil perhitungan nilai matriks partisi baru U yang akan digunakan sebagai penentu suatu lebih cenderung data masuk kedalam satu cluster dengan nilai U paling tinggi diantara cluster lainnya.
Tabel 13. Nilai Derajat Keanggotaan untuk Jumlah 5 Cluster
|
Data ke- |
1 |
2 |
3 |
4 |
5 |
|
1 |
0,8589 |
0,1143 |
0,0084 |
0,0183 |
0,0030 |
|
2 |
0,7535 |
0,2391 |
0,0041 |
0,0106 |
0,0040 |
|
3 |
0,8765 |
0,1146 |
0,0025 |
0,0064 |
0,0045 |
|
34 |
0,0000 |
0,0000 |
0,9998 |
0,0001 |
0,0289 |
35 0,1130 0,3679 0,0642 4548 0,1045
Pada Tabel 13 didapatkan nilai derajat keanggotaan akhir untuk setiap data. Penetuan suatu data masuk kedalam cluster ditentukan dengan cara membandingkan nilai derajat keanggotaannya dalam cluster tersebut dan data akan masuk kedalam cluster dengan nilai derajat keanggotaan yang lebih tinggi.
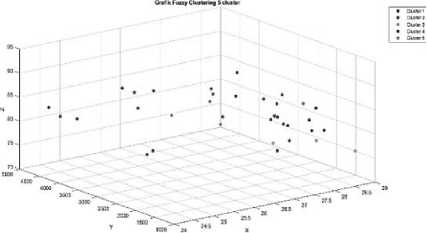
Gambar 5. Grafik Fuzzy Clustering untuk Jumlah 5 Cluster
Pada gambar 5 dapat dilihat grafik hasil pengelompokkan dengan jumlah 5 cluster, hasil pengelompokan yang didapatkan adalah 15 kabupaten (Kab. Boyolali, Kab. Klaten, Kab. Wonogiri, Kab. Karanganyar, Kab. Sragen, Kab. Grobogan, Kab. Pati, Kab. Kudus, Kab. Kendal, Kab. Batang, Kab. Tegal, Kab. Brebes, Kota Semarang, dan Kota Pekalongan) berada di cluster 1 yang berwarna biru, 9 kabupaten (Kab. Banyumas, Kab. Purbalingga, Kab. Purworejo, Kab. Wonosobo, Kab. Magelang, Kab. Sukoharjo, Kab. Demak, Kab. Pekalongan, Kota Magelang, dan Kota Tegal) berada di cluster 2 yang berwarna merah, 3 kabupaten (Kab. Blora, Kab. Pemalang, dan Kota Surakarta) berada di cluster 3 yang berwarna oranye, 4 kabupaten (Kab. Rembang, Kab. Jepara, Kab. Temanggung, dan Kota Salatiga) berada di cluster 4 yang berwarna ungu dan 4 kabupaten (Kab. Cilacap, Kab. Banjarnegara, Kab. Kebumen, dan Kab. Semarang) berada di cluster 5 yang berwarna hijau.
-
c. Uji Validitas Indeks
Uji validitas indeks dilakukan untuk dapat mengetahui jumlah cluster yang paling baik untuk digunakan dalam pengelompokkan pada kasus yang dikerjakan. Uji validitas yang akan digunakan adalah Partition Coefficient (PC) dan Classification Entropy (CE).
-
1. Partition Coefficient
PC(C) = ∑ih∑^μ^2∕35
pc =
[[(0,06138)2+(0,93862)2]+∙+[(0,98938)2+(0,01062)2]]
35
-
2. Classification Entropy
CE(c) = -⅛ι∑⅛k ln (μik)
CE(2) =
[[(-0,24712)+∙∙∙+(-0,01524)]+[(-0,08578)+∙∙∙+(-0,06964)]]
—
35
CE(2) = 0,079792
Hasil uji validitas indeks untuk setiap cluster pada tabel 14.
|
Uji Validitas Indeks |
2 |
3 |
4 |
5 |
|
PC |
0,91123 |
0,88069 |
0,82104 |
0,81469 |
|
CE |
0,07979 |
0,09935 |
0,14639 |
0,15081 |
Tabel 14. Hasil Uji Validitas Indeks
Untuk dapat mengetahui cluster yang optimal, apabila pengujian uji validitas PC dengan nilai yang mendekati 1 dan CE dengan nilai yang mendekati 0. Dari hasil uji validitas index PC dan CE dapat diketahui bahwa jumlah cluster yang optimal adalah 2 cluster dengan nilai PC yaitu 0,911233 (mendekati 1) dan nilai EC yaitu 0,07979 (mendekati 0). Berdasarkan hasil uji validitas yang sudah dilakukan hasil pengelompokkan yang optimal dengan jumlah cluster adalah 2.
-
d. Interpretasi Hasil
Hasil pengelompokkan kabupaten di Provinsi Jawa Tengah dengan metode fuzzy clustering dan berdasarkan hasil uji validitas indeks menujukkan bahwa jumlah cluster yang cocok pada kasus ini adalah 2 cluster.
Tabel 15. Pusat Cluster
|
Pusat Cluster | |||
|
Cluster |
Suhu (°C) |
Curah Hujan (mm) |
Kelembaban Udara (%) |
|
1 |
27.9 |
2418 |
80.4 |
|
2 |
26.6 |
4087 |
81.3 |
Pada tabel 15 dapat diketahui setiap pusat cluster untuk setiap variabel yang digunakan pada pengelompokkan. Informasi yang dapat
diperoleh dari kedua pusat cluster ini yaitu, pada Provinsi Jawa Tengah, kabupaten-kabupaten dapat dikelompokkan menjadi 2 kelompok berdasarkan karakteristik iklim yang ada:
-
1. Kelompok pertama (cluster ke-1), berisi kabupaten yang memiliki rata-rata suhu sekitar 27.9°C; memiliki jumlah curah hujan sekitar 2418mm; memiliki rata-rata kelembaban udara sekitar 80.4%.
-
2. Kelompok kedua (cluster ke-2), berisi kabupaten yang memiliki rata-rata suhu sekitar 26.6°C; memiliki jumlah curah hujan sekitar 4087mm; memiliki rata-rata kelembaban udara sekitar 81.3%
-
4. KESIMPULAN DAN SARAN
Berdasarkan pengelompokkan fuzzy clustering dan uji validitas indeks Partition Coefficient dan Classification Entropy yang telah dilakukan diperoleh hasil
pengelompokkan yang optimal yaitu 2 cluster dengan nilai Partition Coefficient yaitu 0,911233 dan nilai Classification Entropy yaitu 0,07979. Hasil pengelompokkan yang diperoleh adalah sebagai berikut:
-
1. Cluster 1 terdiri dari 12 kabupaten dan 1 kota (Kab. Cilacap, Kab. Banyumas, Kab. Purbalingga, Kab. Banjarnegara, Kab. Kebumen, Kab. Purworejo, Kab. Wonosobo, Kab. Magelang, Kab. Sukoharjo, Kab. Demak, Kab. Semarang, Kab. Pekalongan dan Kota Magelang).
-
2. Cluster 2 terdiri dari 17 kabupaten dan 5 kota (Kab. Boyolali, Kab. Klaten, Kab. Wonogiri, Kab. Karanganyar, Kab. Sragen, Kab. Grobogan, Kab. Blora, Kab. Rembang, Kab. Pati, Kab. Kudus, Kab. Jepara, Kab. Temanggung, Kab. Kendal, Kab. Batang, Kab. Pemalang, Kab. Tegal, Kab. Brebes, Kota Surakarta, Kota Salatiga, Kota Semarang, Kota Pekalongan, dan Kota Tegal).
DAFTAR PUSTAKA
Badan Pusat Statistik. (2023). Provinsi Jawa Tengah dalam Angka 2023.
Bezdek, J. C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press.
Ginting, R. P. (2017). Pengelompokkan Kabupaten/Kota Di Sumatera Utara
Berdasarkan Karakteristik Iklim dengan Analisis Cluster. Skripsi, Universitas Sumatera Utara.
Juaeni, I., Yuliani, D., Ayahbi, R., Noersomadi, Hardjana, T., & Nurzaman. (2010).
Pengelompokkan Wilayah Curah Hujan Kalimantan Barat Berbasis Metode Ward dan Fuzzy clustering. Jurnal Sains Dirgantara, 7(2), 82–99.
Kusumadewi, S., & Purnomo, H. (2013).
Aplikasi Logika Fuzzy. Graha Ilmu.
Nasir, A. A., Handoko, T., Ania, J., Hidayati, R., & Suharsono, H. (2017). Klimatologi Dasar. IPB Press.
Shihab, A. I. (2000). Fuzzy clustering Algorithm and Their Application to Medical Image Analysis. Dissertation, University of London.
Tan, P. N., Steinbach, M., & Kumar, V. (2006). Introduction to Data Mining. Pearson
Education.
Tjasyono, B. (2004). Klimatologi. ITB.
Winarsih, S. (2019). Seri Sains: Iklim. ALPRIN
65
Discussion and feedback