PEMODELAN REGRESI NONPARAMETRIK SPLINE TRUNCATED KASUS KEJADIAN DIARE DI PROVINSI BALI
on
E-Jurnal Matematika Vol. 13(1), Januari 2024, pp. 28-37
DOI: https://doi.org/10.24843/MTK.2024.v13.i01.p438
ISSN: 2303-1751
PEMODELAN REGRESI NONPARAMETRIK SPLINE TRUNCATED KASUS KEJADIAN DIARE DI PROVINSI BALI
Nadiya Yuvita Rizki1§, I Gusti Ayu Made Srinadi2, I Komang Gde Sukarsa3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: nadiyayuvitarizki@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: gedesukarsa@unud.ac.id]
§Corresponding Author
ABSTRACT
Nonparametric regression is a flexible approach used to determine the relationship between the predictor variable and the response variable is unknown. One method that can be used to estimate nonparametric regression models is the truncated spline. The truncated spline is an effective method to estimate nonparametric regression models due to its ability to adapt to the data's characteristics through knots. Truncated spline estimates its parameters with the maximum likelihood estimator (MLE) method and finds the optimal knot points with the minimum generalized cross validation (GCV) value. This study used the truncated spline to model diarrhea cases in Bali Province, examining five variables that could affect incidence. The optimal knot points were 2-1-3-3-2 with a minimum GCV value of 67572,38. The study found that the number of clean drinking water facilities, food management places that meet health requirements, public places that meet health requirements, population density, and access to proper sanitation facilities had a significant effect on diarrhea incidence. The coefficient of determination for this model is 98,87%.
Keywords: Diarrhea, GCV, Knots, Truncated Spline Nonparametric Regression.
-
1. PENDAHULUAN
Pendekatan regresi nonparametrik digunakan untuk mengetahui hubungan antara kedua variabel yaitu variabel prediktor dan variabel respon yang tidak diketahui bentuk kurva regresinya. Pendekatan membebaskan data untuk menemukan bentuk penduganya sendiri (Eubank, 1988). Sehingga, kelebihan dari pendekatan ini adalah fleksibilitasnya yang tinggi dan tidak mengharuskan penggunanya untuk melakukan pemenuhan asumsi-asumsi yang ketat. Beberapa metode yang populer digunakan oleh pendekatan regresi nonparametrik diantaranya histogram, kernel, spline, polinomial lokal, deret fourier, dan lain-lain (Budiantara, 2011).
Regresi spline merupakan salah satu pendekatan regresi nonparametrik yang dimodifikasi dari fungsi polinomial tersegmen (Rumlawang dkk., 2018). Polinomial yang bersegmen itu yang menyebabkan regresi nonparametrik spline termasuk kedalam salah satu jenis piecewise polinomial. Fleksibilitasnya melebihi polinomial biasa pada umumnya, sehingga sangat memungkinkan
dapat melakukan penyesuaian diri lebih efektif terhadap perilaku lokal suatu fungsi atau data. Kemampuannya dalam penyesuaian diri terhadap karakteristik data dinilai lebih efektif, dikarenakan estimator pada spline memiliki sifat truncated atau berupa potongan-potongan polinomial tersegmen yang fleksibel (Hidayat dkk., 2017). Potongan-potongan polinomial inilah yang menjadi kelebihan dari regresi spline atau dinamakan dengan titik knot. Titik knot berisi informasi mengenai perubahan pola perilaku data pada setiap interval berbeda, yang ditunjukkan dengan titik belok pada kurva fungsi. Sehingga bentuk estimasi kurva regresinya menyesuaikan data tanpa dipengaruhi oleh faktor subjektivitas peneliti (Eubank, 2004).
Kelemahan dari fungsi polinomial pada umumnya adalah memiliki sifat global. Sehingga diperlukan pengembangan suatu fungsi yang dapat mempertahankan fungsi polinomial secara lokal. Permasalahan tersebut dapat diatasi dengan fungsi spline truncated (Rositawati dkk., 2019). Dalam memodelkannya, regresi nonparametrik spline
truncated ini akan menentukan orde dan titik knot yang optimal pada suatu fungsi.
Pada penelitian ini, dilakukan penelitian mengenai faktor-faktor yang berpengaruh signifikan terhadap kasus kejadian diare dengan metode regresi nonparametrik spline truncated sekaligus memodelkan hubungan antara kedua variabel tersebut. Penyakit diare tergolong masih relatif tinggi ditemukan di Provinsi Bali. Informasi ini didapatkan dari data Dinas Kesehatan Provinsi Bali dari tahun 2020 hingga 2022. Diperkirakan penemuan jumlah target kasus diare di tahun 2020 sekitar 114.725 kasus, selanjutnya tahun 2021 mencapai angka 118.174, dan pada tahun 2022 mencapai 119.207 kasus. Menurut angka peningkatan yang ditemukan setiap tahun menunjukkan bahwa Provinsi Bali masih belum sempurna dalam penanganan masalah kesehatan, terutama diare. Tujuan dari penelitian ini untuk memodelkan kasus kejadian diare dan menentukan faktor-faktor yang berpengaruh signifikan terhadap kasus kejadian diare di provinsi Bali.
-
2. METODE PENELITIAN
-
2.1 Regresi Nonparametrik Spline
-
Truncated
Secara umum, model regresi nonparametrik didefinisikan sebagai berikut (Eubank, 1999):
Vi = f(td + Zi, i = 1,2, - ,n (1)
dimana yi sebagai variabel respon pengamatan ke-i, f(t{) sebagai fungsi f dari variabel prediktor pada pengamatan ti,... ,tn yang tidak diketahui, dan Zi sebagai galat atau eror dari pengamatan ke-i yang diasumsikan tidak berkorelasi, dengan nilai mean adalah 0 dan nilai varians konstan yaitu σ2.
Berikut fungsi spline truncated f berorde m dengan titik knot Kj1, Kj2,... ,Kjr yang didefinisikan sebagai berikut (Eubank, 1999):
f(tj^ = βθ+βj1tj + βj2tj +—+ βjmtΓ + ∑k=1βj(k+m)(tj - κjk) +
= ∑m=0 βjhtf + ∑kk=l βj(k+m) (tj - Kjk\ (2) dimana,
j = variabel prediktor yang nilainya diketahui, j = 1,2, - ,p
h = derajat polinimial, h = 0,1,2,- ,m k = titik-titik knot, k = 1,2,... , r
m = 1 (karena fungsi regresi nonparametrik spline truncated yang digunakan pada penelitian ini adalah fungsi linier)
dan (tj — Kjk')+ sebagai fungsi truncated yang dapat dijabarkan sebagai berikut:
(tj-κ,k)m={ (i-1^
, tj ≥ Kjk tj < Kjk
(3)
Dari persamaan (1) akan disubstitusikan kedalam persamaan (2) untuk memperoleh model regresi nonparametrik spline truncated, maka secara umum dinyatakan sebagai berikut: yj = ∑m=0βjhtjl + ∑k=1βj(k+m)(tj — Kjk) +
+Zj (4)
Dalam pengestimasian parameter β dapat dilakukan dengan metode Maximum Likelihood Estimator (MLE). Metode MLE ini digunakan apabila distribusi populasinya telah diketahui. Berdasarkan asumsi tj dan Zj pada persamaan (1) yang telah dijelaskan sebelumnya, maka galat yj juga diasumsikan tidak berkorelasi atau berdistribusi normal dengan nilai mean f(ti) dan variansi σ2. Sehingga fungsi densitas peluang yi adalah sebagai berikut: f(y -.f(t∖^) =^exv[-⅛^^
,f(t)>0,σ2>0 (5)
Selanjutnya fungsi likelihood dapat dinyatakan sebagai berikut:
Uy,∩ = ∏j=ιf(yj- ^f(tj},σ2}
= a~σ2} 2(∙yp [— 22⅛∑j=ι (yj - f(tj}) ] (6)
Setelah diperoleh fungsi likelihood, tahap selanjutnya adalah memaksimumkan fungsi likelihood L(y,f} untuk mendapatkan estimasi titik fungsi f sebagai berikut:
max{L(y,∩} =
βmχh[{^^ —
∑m=o βjht<ι + ∑ι=ι βj(m+k) (tj — Kjk)m)2)} (7)
Kemudian menerapkan transformasi logaritma pada persamaan (7) hingga diturunkan secara parsial terhadap β pada persamaan yang telah diperoleh serta di sisi kanannya disamakan dengan nol. Dengan demikian diperoleh:
β = (Kt)-rKy. (8)
Sehingga pengestimasian y dapat diperoleh dengan sebagai berikut:
y = tβ + ε
y = t((t't)-1t'y) + ε
= A(k^)y + ε . (9)
Dimana A(k) menyatakan matriks yang digunakan untuk menghitung nilai generalized cross validation (GCV) dalam menentukan titik knot yang optimal.
-
2.2 Sumber Data
Data yang digunakan dalam penelitian ini adalah jenis data sekunder, yang diperoleh dari Dinas Kesehatan Provinsi Bali Tahun 2022. Unit amatan pada penelitian ini adalah 57 kecamatan pada 9 Kabupaten/Kota di Provinsi Bali.
-
2.3 Variabel Penelitian
Variabel penelitian yang digunakan dapat dilihat pada tabel di bawah ini:
Tabel 1. Variabel Penelitian dan Skala Pengukuran
|
Kode |
Nama Variabel |
|
Variabel respon: | |
|
y |
Kasus kejadian diare |
|
Variabel prediktor: | |
|
Xi |
Jumlah sarana air minum bersih |
|
*2 |
Jumlah TPM (Tempat Pengelolaan Makanan) yang memenuhi syarat kesehatan |
|
X3 |
Jumlah TTU (Tempat-Tempat Umum) yang memenuhi syarat kesehatan |
|
X4 |
Kepadatan penduduk |
|
*5 |
Jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak. |
-
2.4 Teknik Analisis Data
Berikut tahapan teknik dan analisis data:
-
1. Menentukan variabel-variabel
penelitian yang akan digunakan.
-
2. Membuat gambaran umum kasus yang digunakan dimana meliputi statistika deskriptif, dan scatterplot.
-
3. Memodelkan variabel respon dan variabel prediktor menggunakan metode regresi nonparametrik spline truncated dengan satu titik knot, dua titik knot, tiga titik knot, dan kombinasi knot yang berorde linier.
-
4. Menentukan titik knot optimal dengan menggunakan kriteria GCV yang paling minimum dengan langkah-langkah sebagai berikut:
-
a. Menghitung matriks A(k)
-
b. Menghitung nilai Mean Square Error (MSE).
-
c. Menentukan titik knot yang optimal dengan menggunakan nilai GCV yang paling minimum.
-
5. Membuat model regresi nonparametrik spline truncated dengan orde dan titik knot yang optimal.
-
6. Pengujian parameter model regresi nonparametrik spline truncated secara serentak maupun secara parsial.
-
7. Pengujian asumsi residual dengan asumsi Identik, Independen, dan Berdistribusi Normal (IIDN) dari model regresi nonparametrik spline truncated.
-
8. Menghitung nilai koefisien determinasi (R2) model regresi nonparametrik spline truncated.
-
9. Menginterpretasikan model yang telah diperoleh dari regresi nonparametrik spline truncated.
-
10. Menarik kesimpulan dari hasil interpretasi model regresi nonparametrik spline truncated.
-
3. HASIL DAN PEMBAHASAN
-
3.1 Gambaran Umum Kasus Kejadian Diare
-
Gambaran umum kasus kejadian diare di Provinsi Bali dengan kelima variabel yang diduga memengaruhinya dijelaskan melalui tabel statistika dekriptif. Berikut penjelasan tabel statistika deskriptif meliputi rata-rata, nilai minimum, dan nilai maksimum.
Tabel 2. Tabel Statistika Deskriptif
|
Variabel |
Mean |
Min |
Max |
|
y |
2052,807 |
592 |
8530 |
|
X1 |
27,895 |
1 |
279 |
|
*2 |
118,754 |
0 |
555 |
|
X3 |
57,561 |
20 |
128 |
|
X4 |
1549,03 |
177,2 |
8619,5 |
|
X5 |
19305,7 |
4040 |
49828 |
Sebelum penelitian dilanjutkan ke tahap pemodelan, maka perlu diketahui dahulu pola hubungan antara kasus kejadian diare dengan kelima variabel yang diduga memengaruhinya. Pola hubungan kedua jenis variabel dapat diketahui menggunakan bantuan scatterplot. Berikut scatterplot hubungan antara variabel respon dengan masing-masing variabel prediktor.

0 50 100 150 200 250
x1

0 100 200 300 400 500

20 40 60 80 100 120
x3
x2

0 2000 4000 6000 8000
'T*^*
10000 20000 30000 40000 50000
x5
Gambar 1. Scatterplot Hubungan antara Variabel Respon dengan Masing-Masing Variabel
Prediktornya
Berdasarkan gambar tersebut, dapat diperhatikan bahwa scatterplot hubungan antara kasus kejadian diare dengan masing-masing variabel prediktor cenderung tidak membentuk suatu pola tertentu. Sehingga kedua jenis variabel ini dapat dilanjutkan ke tahap pemodelan dengan metode regresi nonparametrik spline truncated.
-
3.2 Pemodelan Kasus Kejadian Diare dengan Regresi Nonparametrik Spline Truncated
Pada tahap ini, langkah pertama yang dilakukan adalah menentukan orde dan titik knot yang optimal. Orde model yang digunakan adalah orde linier atau berorde satu. Titik knot yang dicobakan adalah satu titik knot, dua titik knot, tiga titik knot, dan kombinasi titik knot dengan menggunakan kriteria GCV.
Pada percobaan pertama, pemilihan titik knot optimal dilakukan dengan satu titik knot. Berikut model regresi nonparametrik spline truncated dan hasil 5 iterasi terbaik menggunakan orde satu dan satu titik knot pada Tabel 3.
yj = β0 + β11x1 + β12(x! K11) + + β21x2 + β22(x2
K21) + + β3ix3 + β32(x3 - K31) + + β4ix4 +
β42(x4 - ^41)+ + β51x5 + βΞ2(xΞ - K51) +
Tabel 3. Hasil Iterasi Nilai GCV dengan Satu Titik Knot
|
Banyak Kandidat Titik Knot |
Knot |
GCV | ||||
|
^l |
⅞ |
*3 |
*4 |
⅞ | ||
|
56 |
238,56 |
474,27 |
112,29 |
7391,53 |
43167,93 |
163782,6 |
|
49 |
238,46 |
474,06 |
112,25 |
7388,33 |
43150,58 |
163928,9 |
|
42 |
238,32 |
473,78 |
112,20 |
7384,04 |
43127,32 |
164124,5 |
|
35 |
238,1 |
473,40 |
112,1 |
7378 |
43094,5 |
164399,5 |
|
28 |
237,8 |
472,80 |
112 |
7368,80 |
43044,6 |
164814,7 |
Berdasarkan Tabel 3, terdapat hasil 5 iterasi nilai GCV dan nilai knot untuk masing-masing variabel prediktor. Nilai GCV minimum yang diperoleh pada satu titik knot adalah 163782,6 dengan nilai knot masing-masing variabel prediktor sebagai berikut:
|
Variabel x1 |
: 238,56 |
‰) |
|
Variabel x2 |
: 474,27 |
(^21) |
|
Variabel x3 |
: 112,29 |
(¾1) |
|
Variabel x4 |
: 7391,53 |
‰) |
|
Variabel x5 |
43167,93 (⅛1) | |
Pada percobaan kedua, setelah mendapatkan nilai GCV minimum dengan satu titik knot, selanjutnya pemilihan titik knot optimal dilakukan dengan dua titik knot. Berikut model regresi nonparametrik spline truncated dan hasil 5 iterasi terbaik menggunakan orde satu dan dua titik knot pada Tabel 4.
yj = β0 + β11x1 + β12(x1 K11) + + β13(x1 K12) + +
β21x2 + β22(x2 - K21) + + β23(x2 - K22) +
β31x3 + β32(x3 - K31) + + β33(x3 - K32) +
-
β51x5 + βΞ2(xΞ - ¾1)+ + βΞ3(xΞ - ^Ξ2) +
Tabel 4. Hasil Iterasi Nilai GCV dengan Dua Titik Knot
|
Banyak Kandida t Titik Knot |
Knot |
GCV | ||||
|
*l |
*2 |
*3 |
*4 |
*5 | ||
|
56 |
162,7 5 |
322, 91 |
82,84 |
5089,0 8 |
30680,2 9 |
83907,1 8 |
|
223,4 |
444 |
106,4 |
6931,0 4 |
40670,4 | ||
|
37 |
163,2 |
323, 7 |
83 |
5101,9 |
30749,7 |
83915,6 |
|
224,9 |
447, 1 |
107 |
6977,9 |
40924,8 | ||
|
42 |
163,7 3 |
324, 88 |
83,22 |
5119,0 3 |
30842,7 3 |
83966,6 7 |
|
224,7 6 |
446, 71 |
106,9 3 |
6972,2 2 |
40893,7 6 | ||
|
32 |
162,4 0 |
322, 2 |
82,7 |
5079,2 |
30626,6 |
84018,3 |
|
225,2 |
447, 5 |
107,1 |
6985,5 |
40965,8 | ||
|
51 |
162,2 4 |
321, 9 |
82,64 |
5073,7 3 |
30597,0 4 |
84021,7 1 |
|
223,4 |
444 |
106,4 |
6931,0 4 |
40670,4 | ||
Berdasarkan Tabel 4, terdapat hasil 5 iterasi nilai GCV dan nilai knot untuk masing-masing variabel prediktor. Nilai GCV minimum yang diperoleh pada dua titik knot adalah 83907,18 dengan nilai knot masing-masing variabel prediktor sebagai berikut:
|
Variabel x1 |
: 162,75 |
(K11) ; 223,4 |
(K12) |
|
Variabel x2 |
: 322,91 |
(K21) ; 444 |
(K22) |
|
Variabel x3 |
: 82,84 |
(K31) ; 106,4 |
(K32) |
|
Variabel x4 |
: 5089,08 |
(K41) ; 6931,04 (K42) | |
|
Variabel x5 |
: 30680,29 (K51) ; 40670,4 (K52) | ||
Pada percobaan ketiga, setelah mendapatkan nilai GCV minimum dengan dua titik knot, selanjutnya pemilihan titik knot optimal dilakukan dengan tiga titik knot. Berikut model regresi nonparametrik spline truncated dan hasil 5 iterasi terbaik menggunakan orde satu dan tiga titik knot pada Tabel 5.
.Ar
yj = β0 + β11x1 + β12(x1 - K11) + + β13(x1 - ^12) +
+ β14(x1 - K13) + + β21x2
+ β22(x2-K21)++β23(x2-K22') +
+ β24(x2 - K23) + + β31x3
+ β32(x3-K31)++β33(x3-K32) +
+ β34(x3 - K33) + + β41x4
A^ A
+ β42(x4 - K41) + + β43(x4 - K42) +
AA
+ β44(x4 - K43) + + βS1xS
+ β52(x5 - K51) + + β53(x5 - K52) +
+ βs4(xs-Ks3) +
Tabel 5. Hasil Iterasi Nilai GCV dengan Tiga Titik Knot
|
Banyak Kandidat Titik Knot |
Knot |
GCV | ||||
|
Xi |
Xi |
X3 |
X4 |
X5 | ||
|
35 |
25,53 |
48,97 |
29,53 |
922,11 |
8080,1 2 |
7569 3,15 |
|
197,24 |
391,76 |
96,24 |
6136,4 7 |
36360, 94 | ||
|
205,41 |
408,09 |
99,41 |
6384,7 7 |
37707, 65 | ||
|
45 |
19,95 |
37,84 |
27,36 |
752,81 |
7161,9 1 |
7599 9,91 |
|
165,27 |
327,95 |
83,82 |
5165,8 3 |
31096, 55 | ||
|
222,14 |
441,48 |
105,91 |
6892,6 7 |
40462, 27 | ||
|
31 |
19,53 |
37 |
27,2 |
740,02 |
7092,5 3 |
7620 2,99 |
|
195,6 |
388,5 |
95,6 |
6086,8 1 |
36091, 6 | ||
|
204,87 |
407 |
99,2 |
6368,2 2 |
37617, 87 | ||
|
54 |
27,23 |
52,36 |
30,19 |
973,64 |
8359,6 2 |
7639 5,72 |
|
195,08 |
387,45 |
95,4 |
6070,8 8 |
36005, 21 | ||
|
205,57 |
408,40 |
99,47 |
6389,4 6 |
37733, 06 | ||
|
55 |
21,59 |
41,11 |
28,00 |
802,56 |
7431,7 |
7647 6,91 |
|
165,74 |
328,89 |
84,00 |
5180,0 4 |
31173, 63 | ||
|
222,37 |
441,94 |
106,00 |
6899,7 7 |
40500, 81 | ||
Berdasarkan Tabel 5, terdapat hasil 5 iterasi nilai GCV dan nilai knot untuk masing-masing variabel prediktor. Nilai GCV minimum yang diperoleh pada tiga titik knot adalah 75693,15 dengan nilai knot masing-masing variabel prediktor sebagai berikut:
Variabel x1 : 25,53 (K11) ; 197,24 (K12) ;
Variabel x2 : 48,97 (K21) ; 391,76 (K22) ;
408,09 (K23)
Variabel x3 : 29,53 (K31) ; 96,24 (K32);
Variabel x4 : 922,11 (K41) ; 6136,47 (K42);
6384,77 (K43)
Variabel x5 : 8080,12 (K51) ; 36360,94 (K52) ;
37707,65 (K53)
Pada percobaan terakhir, setelah mendapatkan nilai GCV minimum dengan tiga titik knot, selanjutnya pemilihan titik knot optimal dilakukan dengan kombinasi titik knot. Berikut 5 iterasi terbaik yang dipilih berdasarkan nilai GCV minimum dari kombinasi titik knot pada Tabel 6 sebelum memperkirakan model regresi dengan kombinasi titik knot.
Tabel 6. Hasil Iterasi Nilai GCV dengan Kombinasi Titik Knot
|
Banyak Kandid at Titik Knot |
Variab el |
Kombin asi Titik Knot |
Titik-Titik Knot |
GCV | ||
|
43 |
Xi |
2 |
159,86 |
226,05 |
67572, 38 | |
|
X? |
1 |
462,50 | ||||
|
X3 |
3 |
27,71 |
84,29 |
104,8 6 | ||
|
X4 |
3 |
780,22 |
5202,3 8 |
6810, 4 | ||
|
X5 |
2 |
30204, 57 |
41106, 48 | |||
|
53 |
x1 |
2 |
161,38 |
225,54 |
67612, 50 | |
|
x2 |
1 |
469,62 | ||||
|
x3 |
3 |
28,31 |
84,38 |
105,1 5 | ||
|
x4 |
3 |
826,61 |
5210,1 1 |
6833, 6 | ||
|
x5 |
2 |
30456, 15 |
41022,62 | |||
|
23 |
x1 |
2 |
165,27 |
228,45 |
67696, 38 | |
|
x^ |
1 |
454,09 | ||||
|
x3 |
3 |
29,82 |
88,73 |
103,4 5 | ||
|
x4 |
3 |
944,68 |
5549,5 7 |
6700, 8 | ||
|
x5 |
2 |
31096, 55 |
41502, 91 | |||
|
38 |
x1 |
2 |
166,30 |
226,41 |
67715, 59 | |
|
x^ |
1 |
465,00 | ||||
|
x3 |
2 |
84,22 |
107,57 | |||
|
x4 |
3 |
861,71 |
6109,6 3 |
6337, 8 | ||
|
x5 |
1 |
42402, 92 | ||||
|
31 |
x1 |
2 |
167,80 |
223,4 |
67947, 10 | |
|
x? |
1 |
462,50 | ||||
|
x3 |
2 |
84,80 |
106,4 | |||
|
x4 |
3 |
740,00 |
6086,8 |
6368, 2 | ||
|
x5 |
1 |
42196, 70 | ||||
Berdasarkan Tabel 6, terdapat hasil 5 iterasi nilai GCV dan nilai knot untuk masing-masing variabel prediktor. Kombinasi jumlah titik knot pada masing-masing variabel prediktor yang memiliki nilai GCV minimum diperoleh pada kombinasi 2-1-3-3-2. Nilai GCV minimumnya yaitu 67572,38 dengan nilai knot masing-masing variabel prediktor sebagai berikut:
Variabel x1
Variabel x2
Variabel x3
159,86
462,50
27,71
104,86
(Ku) ; 226,05 (K2) (K21)
(K31) ; 84,29 (K32) ;
(K33)
Variabel x4 : 780,22 (TC41) ; 5202,38 (K42) ;
6810,44 (K43)
Variabel X5 : 30204,57 (K51) ; 41106,48 (K52)
Model regresi nonparametrik spline truncated dari model kombinasi titik knot yang terbentuk yaitu sebagai berikut.
yj = β0 + β11x1 + β12^x1 - K11) + + β13^x1 - K12) + + β21x2
+ P22(X2 - K21) + + β31x3
+ β32(χ3-K31)1++ β33(X3-K32)1
+ β34^3 - K33) + + β41x4
+ β42(x4 - K41) + + β43(x4 - K42) +
+ β44(x4 - K43)+ + β51x5
+ β52(x5-K51)++β53(x5-K52) +
-
3.3 Pemilihan Titik Knot Optimal
Pada tahap ini, seluruh GCV minimum dari masing-masing percobaan titik knot telah diperoleh. Selanjutnya dibandingkan nilai GCV minimum dari satu titik knot, dua titik knot, tiga titik knot, dan kombinasi titik knot pada Tabel 7.
Tabel 7. Perbandingan Nilai GCV Minimum
|
Model |
GCV |
|
1 Knot |
163782,6 |
|
2 Knot |
83907,18 |
|
3 Knot |
75693,15 |
|
Kombinasi Knot 2-13-3-2 |
67572,38 |
Tabel 8. Estimasi Parameter Model
|
Variabel |
Parameter |
Estimasi |
|
βo |
-1,298 | |
|
x1 |
β11 |
0,968 |
|
β12 |
23,561 | |
|
β13 |
10,471 | |
|
x2 |
β21 |
0,054 |
|
β22 |
222,612 | |
|
x3 |
β31 |
18,780 |
|
β32 |
3,956 | |
|
β33 |
-183,546 | |
|
β34 |
-405,231 | |
|
x4 |
β41 |
-0,094 |
|
β42 |
0,804 | |
|
β43 |
-2,595 | |
|
β44 |
6,274 | |
|
x5 |
β51 |
0,035 |
|
β52 |
-0,096 | |
|
β53 |
0,186 |
Hasil estimasi pada tabel tersebut dan hasil iterasi model kombinasi titik knot 2-1-3-3-2 akan disubstitusikan ke model regresi nonparametrik spline truncated terbaik yaitu sebagai berikut:
yj = -1,298 + 0,968x1 + 23,561(x1 - 159,86)+ + 10,471(x1 - 226,05)+ + 0,054x2 + 222,612(x2 -462,50)+ + 18,780x3 + 3,956(x3 - 27,71)+ -183,546(x3 - 84,29)+ - 405,231(x3 -104,86)+ - 0,094x4 + 0,804(x4 - 780,22)+ -2,595(x4 - 5202,38)+ + 6,274(x4 - 6810,44)+ + 0,035x5 - 0,096(x5 - 30204,57)+ + 0,186(x5 -41106,48)+
Berdasarkan Tabel 7, nilai GCV minimum diperoleh pada model regresi dari kombinasi titik knot dengan nilai sebesar 67572,38. Hal ini menunjukkan titik knot optimal berada pada model regresi dengan kombinasi titik knot 2-13-3-2.
-
3.4 Pengestimasian Parameter Model Spline
Truncated Terbaik
Model regresi nonparametrik spline truncated terbaik dibentuk dari titik knot optimal sesuai kriteria nilai GCV yang telah diperoleh. Pada kasus kejadian diare di Provinsi Bali, pemilihan titik knot optimal untuk model regresi terbaik adalah dengan kombinasi titik knot 2-1-3-3-2. Estimasi parameter regresi model regresi disajikan pada Tabel 8.
-
3.5 Pengujian Parameter Model
Pengujian parameter model digunakan ketika ingin mengetahui apakah variabel prediktor memberikan pengaruh yang signifikan atau tidak terhadap kasus kejadian diare di Provinsi Bali. Pengujian parameter model terdiri dari dua tahapan, yakni uji secara serentak terlebih dahulu, kemudian jika terbukti parameter berpengaruh signifikan dilanjutkan uji secara parsial.
Tabel 9. Tabel ANOVA Model Regresi Nonparametrik Spline Truncated
|
Sumber |
df |
SS |
MS |
F, rhιtu∏Q |
P-value |
|
Regresi |
16 |
135900030 |
8493751,85 |
162,47 |
3,274e-31 |
|
Error |
40 |
2091187 |
52279,68 | ||
|
Total |
56 |
137991217 |
- |
Berdasarkan perhitungan Analysis of Variance (ANOVA) pada Tabel 9, dapat dilihat nilai Fhitung(162,47 )>FCo,o5;16;4g)(1,90) dan P-vaiue(3,274e-31)< a(θ05), sehingga keputusan adalah tolak H0 atau minimal ada satu parameter model yang berpengaruh signifikan. Selanjutnya untuk mengetahui model apa saja yang berpengaruh signifikan, maka pengujian parameter model dilanjutkan ke uji parsial.
Tabel 10. Hasil Pengujian Signifikansi Parameter Secara Individu
|
Variabel |
Parameter |
Koefisien |
thitung |
'P-valiie |
|
*1 |
ft, |
0,968 |
0,592 |
0,556 |
|
012 |
23,561 |
5,614 |
6,40e-07 | |
|
(„ |
10,471 |
5,614 |
6,40e-07 | |
|
*2 |
021 |
0,054 |
0,146 |
0,885 |
|
022 |
222,612 |
8,570 |
9,01e-12 | |
|
*3 |
031 |
18,780 |
3,587 |
7,04e-04 |
|
032 |
3,956 |
-0,710 |
0,481 | |
|
033 |
-183,546 |
-8,466 |
1,33e-11 | |
|
034 |
-405,231 |
-5,393 |
1,44e-06 | |
|
*4 |
041 |
-0,094 |
-0,481 |
0,633 |
|
042 |
0,804 |
3,191 |
2,32e-03 | |
|
043 |
-2,595 |
-7,083 |
2,53e-09 | |
|
6,274 |
10,153 |
2,63e-14 | ||
|
*5 |
051 |
0,035 |
3,360 |
1,41e-03 |
|
052 |
-0,096 |
-2,170 |
0,034 | |
|
053 |
0,186 |
1,936 |
0,058 |
Berdasarkan hasil pengujian parameter model dengan uji parsial pada Tabel 10, dapat diperhatikan bahwa pada parameter β11>β21>β32>β41>β53 diperoleh keputusan gagal tolak H0 dikarenakan nilai p-vaιue > α(0,05). Namun untuk parameter lainnya terbukti berpengaruh signifikan. Selanjutnya dapat dilihat pada tabel tersebut bahwa pada setiap variabel-variabel prediktornya masih terdapat parameter lainnya yang signifikan, maka secara umum parameter kelima variabel prediktor tersebut terbukti berpengaruh signifikan.
-
3.6 Pengujian Asumsi Residual
Pengujian asumsi residual diperlukan ketika model terbaik dari regresi nonparametrik spline truncated telah ditemukan. Tujuannya untuk mengetahui apakah residual dari model regresi yang dihasilkan telah memenuhi asumsi residual atau tidak. Adapun yang meliputi pengujian asumsi residual yaitu Identik, Independen, dan Berdistribusi Normal (IIDN).
Tabel 11. Tabel ANOVA dari Uji Glejser
|
Sumber |
df |
SS |
MS |
1 hitung |
p-ualue |
|
Regresi |
16 |
320007,9 |
20000,497 |
0,887 |
0,5881 |
|
Error |
40 |
902480,8 |
22562,02 | ||
|
Total |
56 |
1222489 |
- |
Berdasarkan perhitungan Analysis of Variance (ANOVA) dari uji Glejser pada Tabel 11, dapat dilihat nilai Fhltung(0,887) <
F(O,O5;16;4O)(1,9O) dan P-ιmhie(0,5881)> “(o,o5), sehingga keputusan adalah gagal tolak Ho. Kesimpulan yang didapatkan adalah varians residual tidak terjadi heteroskedastisitas atau residual memenuhi uji asumsi identik.
Pengujian asumsi residual selanjutnya adalah uji asumsi independen. Pengujian ini dilakukan dengan melihat plot Autocorrelation Function (ACF).
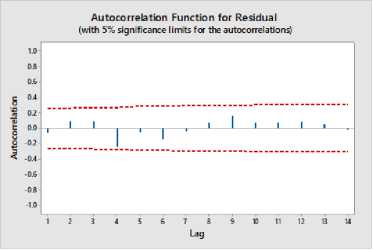
Gambar 2. Plot ACF dari Residual Model Regresi
Berdasarkan hasil Plot ACF pada Gambar 2, dapat diperhatikan bahwa tidak ada nilai autokorelasi pada lag yang keluar melewati batas signifikansi. Sehingga keputusan adalah gagal tolak H0 atau tidak terdapat korelasi antar residual. Hal ini menunjukkan bahwa asumsi independen residual terpenuhi. Pengujian ini dilakukan dengan uji Kolmogorov-Smirnov.
Berdasarkan hasil uji Kolmogorov-Smirnov pada residual model regresi nonparametrik spline truncated, diperoleh nilai 0(0,1602) < ‰ei(0,179) dan P-rαiue(O,O959) > α(o,o5), sehingga keputusan adalah gagal tolak H0. Kesimpulan yang didapatkan adalah residual model regresi memenuhi uji asumsi berdistribusi normal.
Seluruh pengujian asumsi residual yang meliputi uji Identik, uji Independen, dan uji Berdistribusi Normal (IIDN) terbukti dapat terpenuhi. Sehingga dapat disimpulkan bahwa model regresi nonparametrik spline truncated yang terbentuk layak untuk menjelaskan hubungan antara variabel respon dan variabel prediktor dari kasus kejadian diare di Provinsi Bali.
-
3.7 Koefisien Determinasi (R2)
Salah satu indikasi model dikatakan baik jika nilai koefisien determinasi (R2) yang dihasilkan tinggi. Berdasarkan perhitungan Analysis of Variance (ANOVA) dari Uji Glejser, diperoleh nilai Sum of Square Regression (SSR) sebesar 135900030 dan nilai
Sum of Square Total (SST) sebesar 137991217. Sehingga dari nilai SSR dan SST yang diperoleh, maka didapatkan nilai koefisien determinasi (R2) sebesar 0,9848 atau sama dengan 98,48%. Nilai R2 yang diperoleh ini menunjukkan bahwa model dapat menerangkan variasi-variabel respon sebesar 98,48%. Dengan nilai R2 yang tergolong tinggi dapat dikatakan model regresi nonparametrik spline truncated yang terkontruksi merupakan model yang baik.
-
3.8 Interpretasi Model Regresi
Nonparametrik Spline Truncated
Interpretasi model digunakan untuk mengetahui seberapa besar pengaruh masing-masing variabel prediktor yang terbukti signifikan dengan kasus kejadian diare di Provinsi Bali. Adapun variabel-variabel prediktor yang terbukti signifikan adalah jumlah sarana air minum bersih (I1), jumlah TPM (Tempat Pengelolaan Makanan) yang memenuhi syarat kesehatan (i2), jumlah TTU (Tempat-Tempat Umum) yang memenuhi syarat kesehatan (i3), kepadatan penduduk (i4), dan jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak (i5). Berikut hasil interpretasi model terbaik pada masing-masing variabel prediktor:
-
1. Hubungan antara jumlah sarana air minum bersih (I1) dengan kasus kejadian diare (y) dengan mengasumsikan variabel lain nilainya tetap atau konstan adalah sebagai berikut:
yj = 0,968i1 + 23,561(i1 -159,86)1+ + 10,471(i1 - 226,05)+
[ 0,968i1 ; I1 < 159,86 { -3766,46 + 24,53i1 ; 159,86 ≤ I1 < 226,05 ( -6133,43+ 35i1 ; I1 ≥ 226,05
Berdasarkan model tersebut dapat ditarik kesimpulan, jika pada suatu wilayah memiliki jumlah sarana air minum bersih kurang dari 159,86 maka setiap terjadi kenaikan jumlah sarana air minum bersih sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare naik sebanyak 1 kasus. Selanjutnya, jika pada suatu wilayah memiliki jumlah sarana air minum bersih berada antara rentang 159,86 dan 226,05 maka setiap terjadi kenaikan jumlah sarana air minum bersih sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare naik secara signifikan sebanyak 25 kasus. Kemudian, jika pada suatu wilayah memiliki jumlah sarana air minum bersih lebih dari 226,05 maka setiap terjadi kenaikan jumlah sarana air minum bersih sebanyak 1 satuan, maka kasus kejadian
diare naik secara signifikan sebanyak 35 kasus. Terjadi inkonsistensi dalam interpretasi model hubungan antara jumlah sarana air minum bersih dengan kasus kejadian diare karena ada kemungkinan terdapat pengaruh dari variabel-variabel lain di luar variabel penelitian, yakni variabel biologis.
-
2. Hubungan antara jumlah TPM (Tempat Pengelolaan Makanan) yang memenuhi syarat kesehatan (ι2) dengan kasus kejadian diare (y) dengan mengasumsikan variabel lain nilainya tetap atau konstan adalah sebagai berikut:
yj = 0,054i2 + 222,612(i2 - 462,50)1+
_ f 0,054i2 ; I2 < 462,50
= (-102958,05+ 222,67i2 ; I2 ≥ 462,50
Berdasarkan model tersebut dapat ditarik kesimpulan, jika pada suatu wilayah memiliki jumlah TPM yang memenuhi syarat kesehatan kurang dari 462,50 maka setiap terjadi kenaikan jumlah TPM yang memenuhi syarat kesehatan sebanyak 10 satuan, mengakibatkan kasus kejadian diare akan naik sebanyak 1 kasus. Selanjutnya, jika pada suatu wilayah memiliki jumlah TPM yang memenuhi syarat kesehatan lebih dari 462,50 maka setiap terjadi kenaikan jumlah TPM yang memenuhi syarat kesehatan sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare naik secara signifikan sebanyak 223 kasus. Terjadi inkonsistensi dalam interpretasi model hubungan antara jumlah TPM yang memenuhi syarat kesehatan dengan kasus kejadian diare karena ada kemungkinan terdapat pengaruh dari variabel-variabel lain di luar variabel penelitian, yakni variabel biologis. 3. Hubungan antara jumlah TTU (Tempat-
Tempat Umum) yang memenuhi syarat kesehatan (i3) dengan kasus kejadian diare (y) dengan mengasumsikan variabel lain nilainya tetap atau konstan adalah sebagai berikut:
yj = 18,780i3 + 3,956(i3 - 27,71)1+ - 183,546(i3 - 84,29)1+
-405,231(i3 - 104,86)1+
( 18,780i3 ; I3 < 27,71
-109,62 + 22,74i3 ; 27,71 ≤ I3 < 84,29
15361,47 - 160,81i3 ; 84,29 ≤ I3 < 104,86
57853,99- 566,041i3 ; i3 ≥ 104,86
Berdasarkan model tersebut dapat ditarik kesimpulan, jika pada suatu wilayah memiliki jumlah TTU yang memenuhi syarat kesehatan kurang dari 27,71 maka setiap terjadi kenaikan jumlah TTU yang memenuhi syarat kesehatan sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare naik sebanyak 19 kasus.
Kemudian, jika pada suatu wilayah memiliki jumlah TTU yang memenuhi syarat kesehatan berada antara rentang 27,71 dan 84,29 maka setiap terjadi kenaikan jumlah TTU yang memenuhi syarat kesehatan sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare naik secara signifikan sebanyak 23 kasus. Namun, jika pada suatu wilayah memiliki jumlah TTU yang memenuhi syarat kesehatan berada antara rentang 84,29 dan 104,86 maka setiap terjadi kenaikan jumlah TTU yang memenuhi syarat kesehatan sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare turun secara signifikan sebanyak 161 kasus. Selanjutnya, jika pada suatu wilayah memiliki jumlah TTU yang memenuhi syarat kesehatan lebih dari 104,86 maka setiap terjadi kenaikan jumlah TTU yang memenuhi syarat kesehatan sebanyak 1 satuan, akan mengakibatkan kasus kejadian diare turun secara signifikan sebanyak 566 kasus.
-
4. Hubungan antara kepadatan penduduk (x4) dengan kasus kejadian diare (y) dengan mengasumsikan variabel lain nilainya tetap atau konstan adalah sebagai berikut:
yj = -0,094x4 + 0,804(x4 - 780,22)+ - 2,595(i4 - 5202,38)1+
+ 6,274(x4 - 6810,44)1+
(-0,094x4 ; X4 < 780,22
-627,30 + 0,898x4 ; 780,22 ≤ X4 < 5202,38
12872,88 - 1,697x4 ; 5202,38 ≤ X4 < 6810,44
-29885,82 + 4,58x4 ; X4 ≥ 6810,44
Berdasarkan model tersebut dapat ditarik kesimpulan, jika pada suatu wilayah memiliki kepadatan penduduk kurang dari 780,22 maka setiap terjadi kenaikan angka kepadatan penduduk sebanyak 10 jiwa/km2, akan mengakibatkan kasus kejadian diare turun sebanyak 1 kasus. Lalu, jika pada suatu wilayah memiliki kepadatan penduduk berada antara rentang 780,22 dan 5202,38 maka setiap terjadi kenaikan angka kepadatan penduduk sebanyak 10 jiwa/km2, akan mengakibatkan kasus kejadian diare naik sebanyak 9 kasus. Selanjutnya, jika suatu wilayah memiliki kepadatan penduduk berada antara rentang 5202,38 dan 6810,44 maka setiap terjadi kenaikan angka kepadatan penduduk sebanyak 10 jiwa/km2, akan mengakibatkan kasus kejadian diare mengalami penurunan sebanyak 17 kasus. Namun, jika pada suatu wilayah memiliki kepadatan penduduk lebih dari 6810,44 maka setiap terjadi kenaikan angka kepadatan penduduk sebanyak 1 jiwa/km2, akan mengakibatkan kasus kejadian diare naik secara signifikan sebanyak 46 kasus. Terjadi
inkonsistensi dalam interpretasi model hubungan antara kepadatan penduduk dengan kasus kejadian diare karena ada kemungkinan terdapat pengaruh dari variabel-variabel lain di luar variabel penelitian, yakni variabel biologis. 5. Hubungan antara jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak (x5) dengan kasus kejadian diare (y) dengan mengasumsikan variabel lain nilainya tetap atau konstan adalah sebagai berikut:
yj = 0,035x5 - 0,096(x5 - 30204,57)1+
+ 0,186(x5 -41106,48 )1+
0,035x5 ; X5 < 30204,57
2899,64-0,061x5 ; 30204,57 ≤ X5 < 41106,48 -4746,17 + 0,125x5 ; X5 ≥ 41106,48
Berdasarkan model tersebut dapat ditarik kesimpulan, jika suatu wilayah memiliki jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak kurang dari 30204,57 maka setiap terjadi kenaikan jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak sebanyak 100 satuan, akan mengakibatkan kasus kejadian diare naik sebanyak 4 kasus. Namun, jika suatu wilayah memilki jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak berada antara 30204,57 dan 41106,48 maka setiap terjadi kenaikan jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak sebanyak 100 satuan, akan mengakibatkan kasus kejadian diare turun sebanyak 6 kasus. Selanjutnya, jika suatu wilayah memiliki jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak lebih dari 41106,48 maka setiap terjadi kenaikan jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak sebanyak 100 satuan, akan mengakibatkan kasus kejadian diare mengalami kenaikan secara sebanyak 13 kasus. Terjadi inkonsistensi dalam interpretasi model hubungan antara jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak dengan kasus kejadian diare karena ada kemungkinan terdapat pengaruh dari variabel-variabel lain di luar variabel penelitian, yakni variabel biologis.
-
4. KESIMPULAN DAN SARAN
-
4.1 Kesimpulan
-
Berdasarkan rumusan masalah dan hasil pembahasan yang dilakukan, maka diperoleh kesimpulan bahwa titik knot optimal yang digunakan dalam model regresi nonparametrik spline truncated terbaik diperoleh dari
kombinasi titik knot sesuai kriteria nilai GCV. Berdasarkan hasil yang diperoleh pada pemodelan kasus kejadian diare di Provinsi Bali, pemilihan titik knot optimal untuk model regresi terbaik adalah dengan kombinasi titik knot 2-1-3-3-2 dengan nilai GCV minimum sebesar 67572,38. Berikut model spline truncated yang digunakan:
yj = -1,298 + 0,968x1 + 23,561(x1 -159,86)+ +
10,471(x1 - 226,05)+ + 0,054x2 + 222,612⅛, -462,50)+ + 18,780x3 + 3,956(x3 - 27,71)+ -183,546(x3 - 84,29)+ - 405,231(x3 -104,86)+ - 0,094x4 + 0,804(x4 - 780,22)+ -2,595(x4 - 5202,38)+ + 6,274(x4 - 6810,44)+ + 0,035x5 - 0,096(x5 - 30204,57)+ + 0,186(x5 -41106,48 )+
Variabel-variabel prediktor yang terbukti berpengaruh signifikan dari model tersebut adalah jumlah sarana air minum bersih (%1), jumlah TPM (Tempat Pengelolaan Makanan) yang memenuhi syarat kesehatan (%2), jumlah TTU (Tempat-Tempat Umum) yang memenuhi syarat kesehatan (x3), kepadatan penduduk (x4), dan jumlah penduduk dengan akses terhadap fasilitas sanitasi yang layak (%5). Dapat disimpulkan seluruh variabel prediktor berpengaruh signifikan. Nilai koefisien determinasi (Z?2) yang diperoleh dari model terbaik ini sebesar 0,9847 atau sama dengan 98,48%, dapat dikatakan model regresi nonparametrik spline truncated yang terkonstruksi merupakan model yang baik untuk memodelkan kasus kejadian diare di Provinsi Bali.
-
4.2 Saran
Adapun saran yang dapat diberikan penulis untuk penelitian selanjutnya adalah sebagai berikut.
-
1. Penelitian ini dibatasi pada tiga titik knot, selanjutnya diharapkan pada penelitian selanjutnya dapat menambahkan lebih dari tiga titik knot.
-
2. Penelitian ini dibatasi pada orde linier, selanjutnya diharapkan pada penelitian selanjutnya dapat menambahkan orde lainnya seperti orde kuadratik dan kubik dengan kombinasi titik knot sehingga memungkinkan memperoleh hasil yang lebih baik.
-
3. Pada penelitian ini hanya menggunakan variabel prediktor nonbiologis, selanjutnya diharapkan pada penelitian selanjutnya
menambahkan variabel prediktor biologis pada kasus kejadian diare di Provinsi Bali ini.
DAFTAR PUSTAKA
Budiantara, I.N. 2011. Penelitian Bidang Regresi Spline Menuju Terwujudnya Penelitian Statistika yang Mandiri dan Berkarakter. Prosiding Seminar Nasional FMIPA Undiksha.
Dinas Kesehatan Provinsi Bali. 2022. Profil Kesehatan Provinsi Bali 2022. Denpasar: Dinas Kesehatan Provinsi Bali.
Eubank, R. 1988. Spline Smoothing and Nonparametric Regression. New York: Marcel Dekker.
Eubank, R.L. 1999. Nonparametric Regression and Spline Smoothing (2nd ed). New York: Marcel Dekker.
Eubank, R.L. 2004. A Simple Smoothing Spline, III, Comput. Stat. Vol.19(2), pp.227-241.
Hidayat, R., Yuliani. & Sam, M. 2017. Model Regresi Nonparametrik dengan Pendekatan Spline Truncated. Prosiding Seminar
Nasional. Vol.3(01), pp.203-210.
Rositawati, A.F.D., & Budiantara, I.N. 2019. Pemodelan Indeks Kebahagian Provinsi di Indonesia Menggunakan Regresi Nonparametrik Spline Truncated. Jurnal Sains dan Seni ITS. Vol.8(02).
Rumlawang, F.Y., Aulele, S.N., & Kasim, N. 2018. Penentuan Model Regresi Nonparametrik Spline pada Data Pertumbuhan Balita di Desa Nania Provinsi Maluku Tahun 2013-2014. Barekeng: Jurnal Ilmu Matematika dan Terapan. Vol.12(01), pp.27-32.
37
Discussion and feedback